Forced vibration of bending thick rectangular plates with different boundary conditions under concentrated load
2022-12-19CHENYingjieYUEXingyu
CHEN Ying-jie, YUE Xing-yu *
(1.College of Civil Engineering and Mechanics,Yanshan University,Qinhuangdao 066000,China;2.Hebei Province Civil Engineering Key Laboratory of Green Construction and Intelligent Operation and Maintenance,Qinhuangdao 066000,China)
Abstract: The boundary integral method is used to study the forced vibration of thick rectangular plates under three complex boundary conditions,namely,simply supported on four sides,fixed two opposite sides and simply supported on two opposite sides,and fixed on four sides.The solution process is clear,and the governing equations of forced vibration and the equations of the flexural surface are given.Through numerical calculation on the Matlab platform,the calculation results in the form of charts are obtained,and compared with the finite element simulation results.From the comparison of these results the accuracy of applying the boundary integral method to solve the forced vibration problem of thick rectangular plates and the correctness of the derived governing equations and the flexural surface equations can be seen.It has certain practical significance for various related problems in engineering practice,and provides a new way for solving such problems,which can be directly applied to engineering practice.
Key words: theory of thick plates;boundary integral method;the forced vibration;the boundary conditions;numerical calculation;the deflection surface equations
1 Introduction
Thick plate structure theory has been widely used in modern science and technology and production activities[1].It not only has a large number of theoretical basis for the protection engineering and atomic energy engineering of thick plate components,but also needs to involve and apply the thick plate structure theory in modern engineering such as aviation,aerospace and ships[2].At the same time,the forced vibration of thick plate is also inevitable,and the research on the vibration of thick plate is becoming more and more important[3].However,since the thin plate does not consider the influence of shear deformation on bending,the classical thin plate theory cannot meet the accuracy requirements[4-7].Therefore,it is very necessary to propose a new method to solve the thick plate problem.
In the middle of the 20t hcentury,Reissner[8-10]considered the influence of shear deformation and extrusion deformation,and deduced the static equation of thick plate problem.Mindlin[10,11]considered the influence of transverse shear deformation and rotational inertia,and deduced the dynamic equation of bending vibration of thick plates.Up to now,the thick plate theory proposed by Reissner and Mindlin is still widely used by modern scholars as the basic equation for studying thick plate problems.
Based on Mindlin plate theory,Wu et al.[12]solved the free vibration problem of plate with arbitrary shape by using differential cubature method.The typical examples of thick plate bending are calculated in detail based on Hamilton method[13].Based on Mindlin plate theory,Li et al.[14]proposed a high-order eight-node hybrid stress quadrilateral element,and analyzed the bending and free vibration of simply supported,clamped square plates and circular plates with different thickness-span ratios.
Among the existing theories for solving thick plate components,the Reissner theory is the best,while this paper studies the forced vibration of thick rectangular plates by using the boundary integral method on the basis of the Reissner theory.This provides a new method for studying the forced vibration of thick rectangular plates.
2 Forced vibration of simply supported thick rectangular plate on four sides
2.1 Deflection surface equations
According to the governing equation[15],the governing equation of forced vibration of the thick plate is
(1)
wherehis the thickness of the plate,kis the volume modulus,andDis the bending stiffness of the plate.
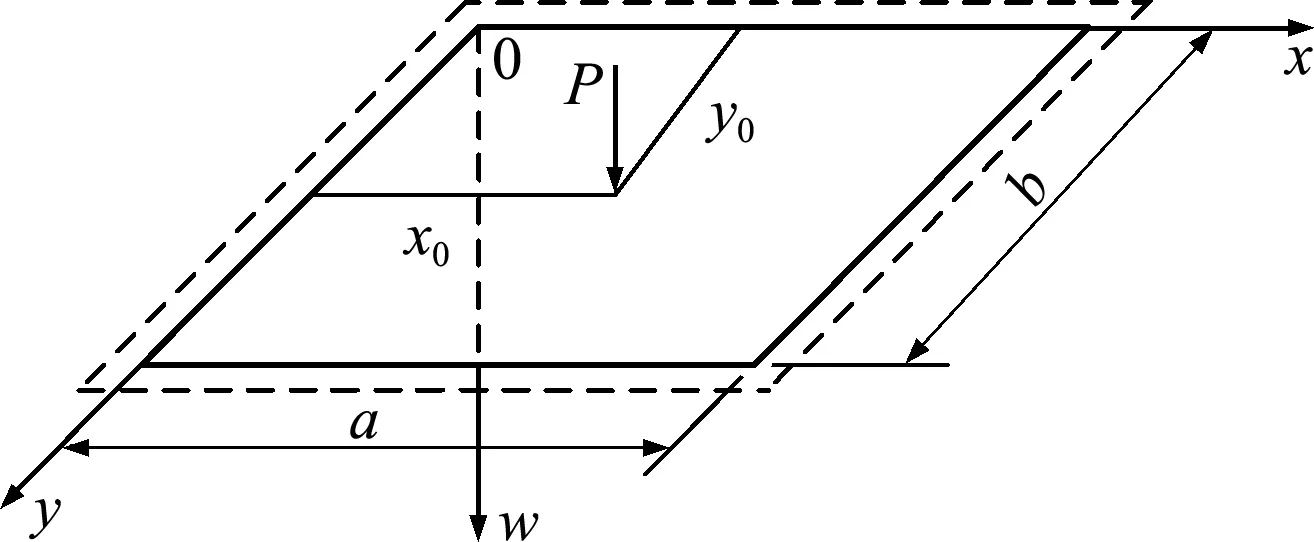
Fig.1 Amplitude actual system of simply supported thick rectangular plate with four sides under concentrated load
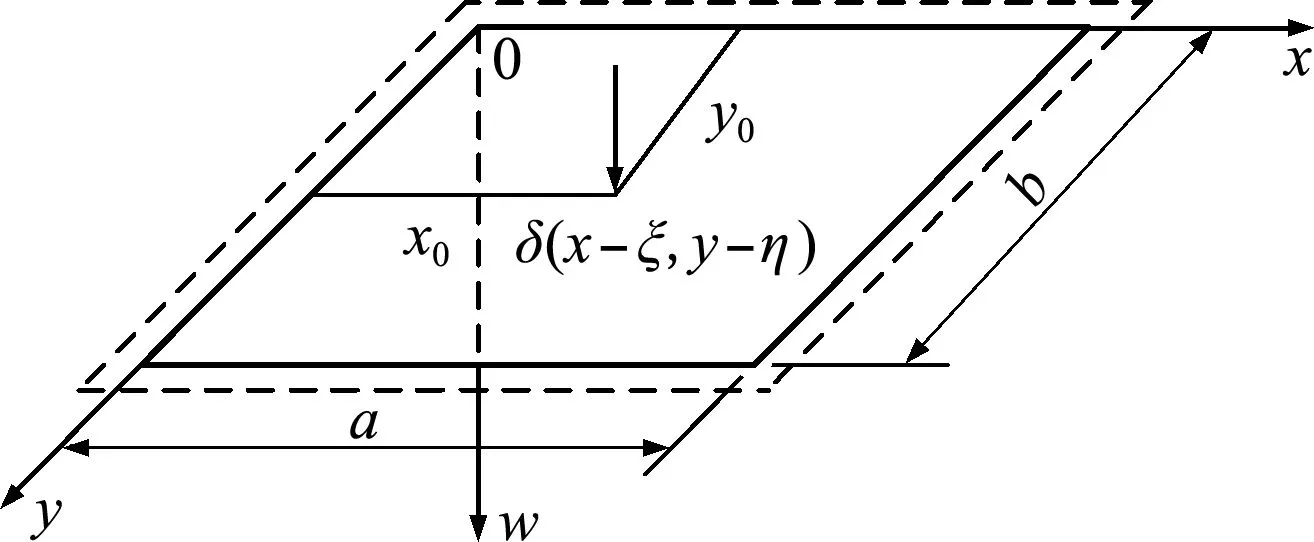
Fig.2 Amplitude quasi-basic system of bending thick rectangular plate
The simply supported thick rectangular plate with four sides under a concentrated load shown in Fig.1 is taken as the amplitude actual system.The bending thick rectangular plate simply supported on four sides under a unit of concentrated load shown in Fig.2 is taken as the quasi-basic system.w1represents the deflection of the basic system andwrepresents the deflection of the actual system.
The boundary integral method is applied between the amplitude actual system of simply supported four sides shown in Fig.1 and the quasi-basic system shown in Fig.2,
(kh2/10)P2δ(x-x0,y-y0)+
(2)
From Ref.[15],it can be seen that the expressions ofw1are
(0≤x≤ξ)(3)
(ξ≤x≤a)(4)
The other two forms of deflection curve equation can be found in Ref.[15],here is no longer given.
The expressions ofw1are substituted into Eq.(2),and the deflection surface equations can be obtained by simplifying the calculation.
2.2 Stress function
Assuming that the stress function is

(5)
(6)
The stress function should satisfy-=0,which will be proved by the following formula

(7)
It can be seen from Eq.(7) that the assumed stress function satisfies the condition.
The bending moments of the simply supported bending thick rectangular plate on four sides are 0,and the following equation can be obtained
En=Fn=Gm=Hm=0
(8)
At this time,only the deflection surface equations and the assumed stress function equation are substituted into the expression to solve the bending moment amplitude of the thick rectangular plate.
Substitute Eq.(8) into the stress function expression (5),and get
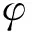
(9)
Then,according to the four-side torsion angles of the simply supported bending thick rectangular plate are zero,E0=F0=G0=H0=0.
At this time,only the deflection surface equations and the assumed stress function equation are substituted into equationsωxandωy.Therefore,the final expression of stress function is
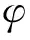
(10)
2.3 Numerical calculation
Combined with practical engineering application,taking the basic parameters:x0=y0=0.5 m (i.e.concentrated loadPacting on the center point of rectangular plate),a=b=1 m,P=100 N,E=200 GPa,v=0.3,h/a=0.1,0.2,0.3,the frequency range isω/ω0=0.1,0.3,0.5,0.6.The deflection curves of simply supported rectangular plate on four sides are obtained by numerical calculation.
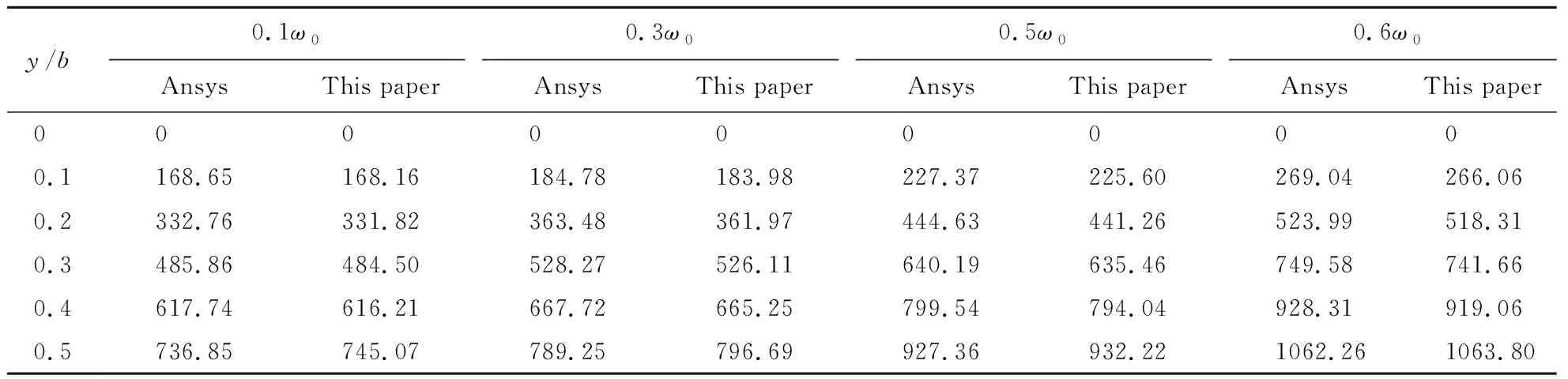
Tab.1 Finite element method and the method in this paper are used to calculate the deflection values of a forced vibration plate with four sides simply supported (h /a =0.1,x /a =0.5) 10-10m

Tab.2 Finite element method and the method in this paper are used to calculate the deflection values of a forced vibration plate with four sides simply supported (h /a =0.2,x /a =0.5) 10-10m
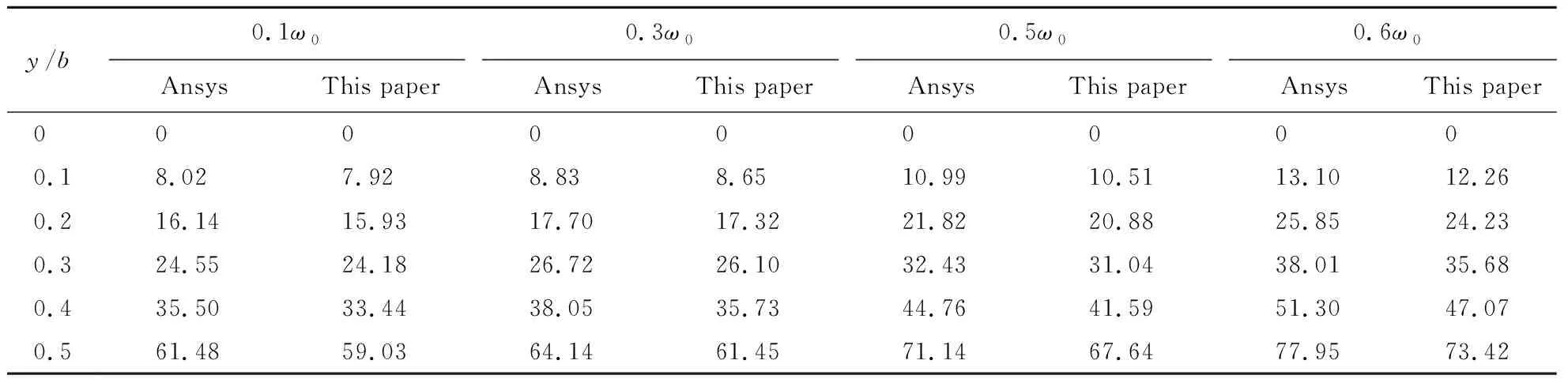
Tab.3 Finite element method and the method in this paper are used to calculate the deflection values of a forced vibration plate with four sides simply supported (h /a =0.3,x /a =0.5) 10-10m
3 Numerical examples
3.1 Deflection surface equations
Firstly,the bending thick rectangular plate with two opposite sides fixed and two opposite sides simply supported under a concentrated load is taken as numerical example ①,Fig.3 is taken as the amplitude actual system.The bending moment constraints of the two fixed sides are removed and replaced by the distributed bending momentsMx 0andMx a,so the equivalent diagram of the amplitude actual system shown in Fig.4,and assume
(11)
(12)

Fig.3 Amplitude actual system of bending thick rectangular plate with two opposite sides fixed and two opposite sides simply supported
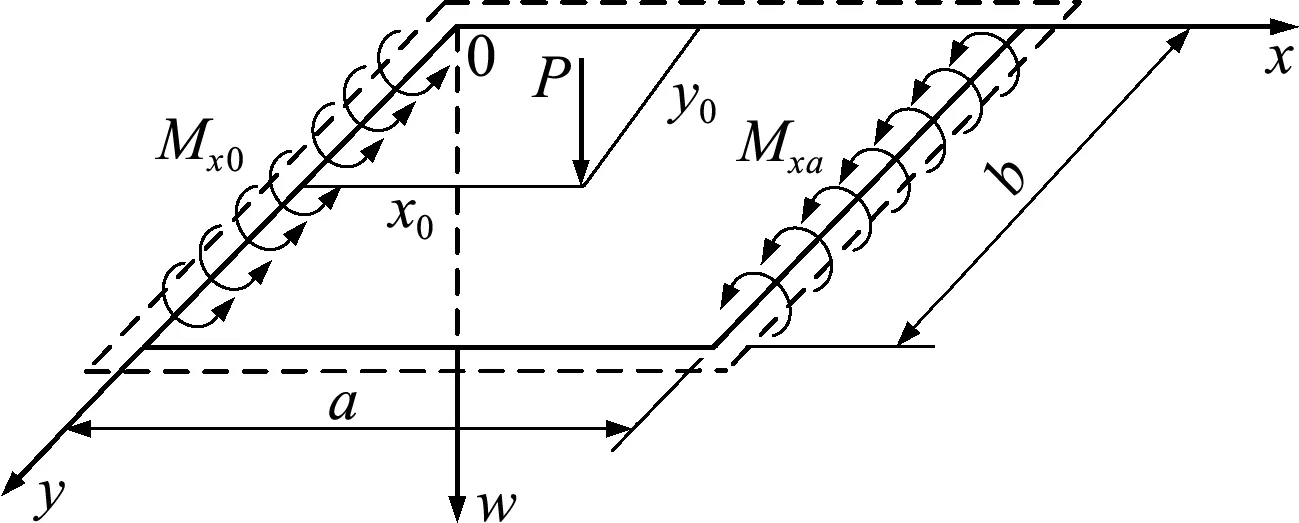
Fig.4 Actual system equivalent diagram of the amplitude of bending thick rectangular plate with two opposite sides fixed and two opposite sides simply supported
In addition,a thick rectangular plate with four fixed sides under concentrated force is taken as numerical example ②.Assuming that the bending moments are
(13)
(14)
(15)
(16)
For thick rectangular plates with the above two boundary conditions,the boundary integral method is applied between the equivalent diagram of the corresponding amplitude actual system and the amplitude quasi-basic system.The expressions of the deflection and boundary angles of the basic system given in Ref.[15] are substituted into the equation,and the deflection surface equations can be obtained after calculation and simplification.
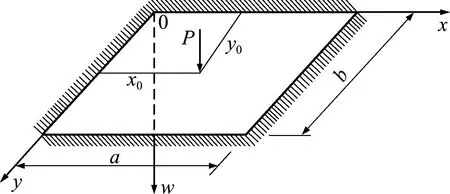
Fig.5 Amplitude actual system of bending thick rectangular plate with fixed four sides

Fig.6 Actual system equivalent diagram of the amplitude of bending thick rectangular plate with fixed four sides
3.2 Stress function
For example ①,the bending thick rectangular plate with two opposite sides fixed and two opposite sides simply supported can be considered as a simply supported bending thick rectangular plate with four sides subjected to distributed bending moment respectively.From the foregoing,it can be seen that theE0=F0=G0=H0=0,Gm=Hm=0 of the four-sided simply supported thick rectangular plate,so the stress function here assumes that
(17)
Since the internal bending moment caused by each deflection is balanced with the external bending moment,the stress function of this boundary condition can be obtained by calculation.
For example ②,the stress function is directly given here
[αm/(γmsinhγmb)] cosαmζ
(18)
3.3 Boundary conditions
For example ①,the deflection surface equations and stress function should satisfy the following boundary conditions
ωζ ζ 0=ωζ ζ a=0
(19)
The deflection surface equations and the stress function are substituted into the boundary conditions, and the boundary condition execution equations can be derived by calculation.Then the boundary execution equations are combined to obtain the values of unknown quantitiesAnandBn.
For numerical example ②,the following boundary conditions should be satisfied to obtain the values of unknown quantitiesAn,Bn,CmandDm
ωζ ζ 0=ωζ ζ a=ωη η 0=ωη η b=0
(20)
3.4 Numerical calculation
For the above two examples,taking the size and mechanical parameters of the plate as the same as 2.3,and the calculation results of example ① are listed in Tables 4 to 6,the numerical results of example ② are shown in Fig.7 to Fig.9.
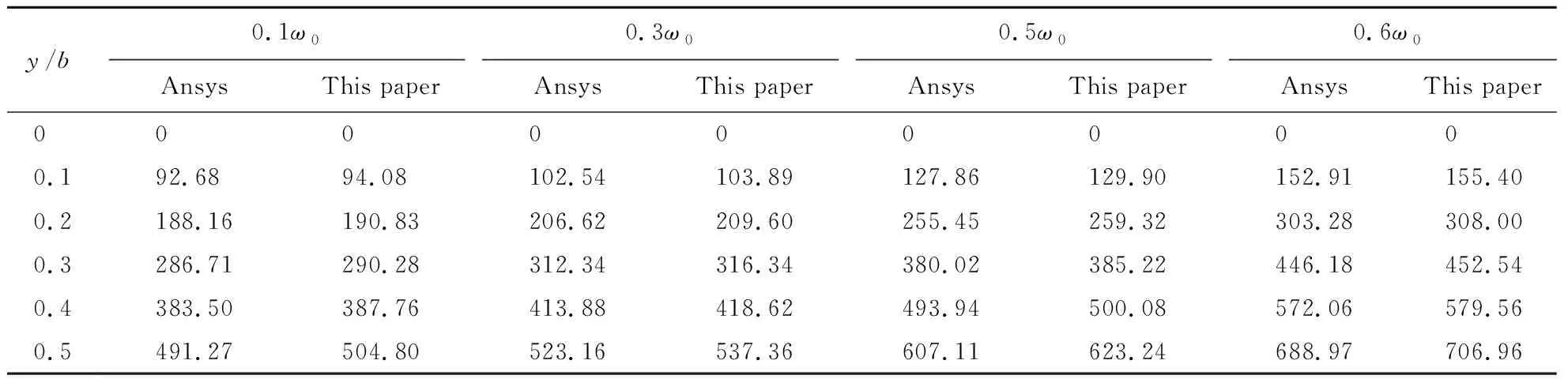
Tab.4 Finite element method and the method in this paper are used to calculate the deflection values of a forced vibration plate with two opposite sides simply supported,two opposite sides fixed (h /a =0.1,x /a =0.5) 10-10m
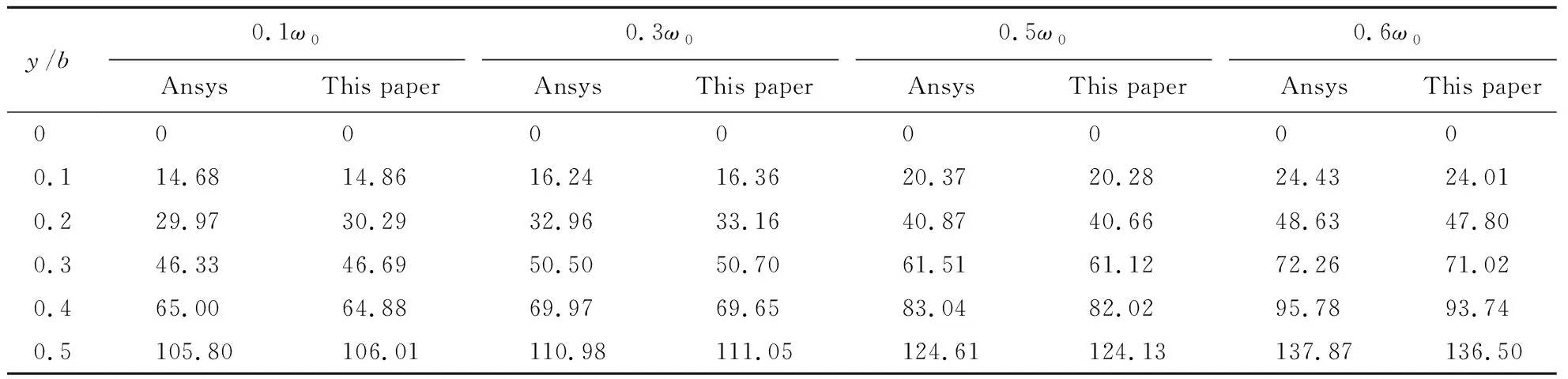
Tab.5 Finite element method and the method in this paper are used to calculate the deflection values of a forced vibration plate with two opposite sides simply supported,two opposite sides fixed (h /a =0.2,x /a =0.5) 10-10m

Tab.6 Finite element method and the method in this paper are used to calculate the deflection values of a forced vibration plate with two opposite sides simply supported,two opposite sides fixed (h /a =0.3,x /a =0.5) 10-10m
For the above two examples,the derivation process of the deflection surface equations,the stress function and the boundary execution equations is similar to that of the thick rectangular plate simply supported on four sides.Therefore,due to the limitation of space,it is no longer specified in this chapter.
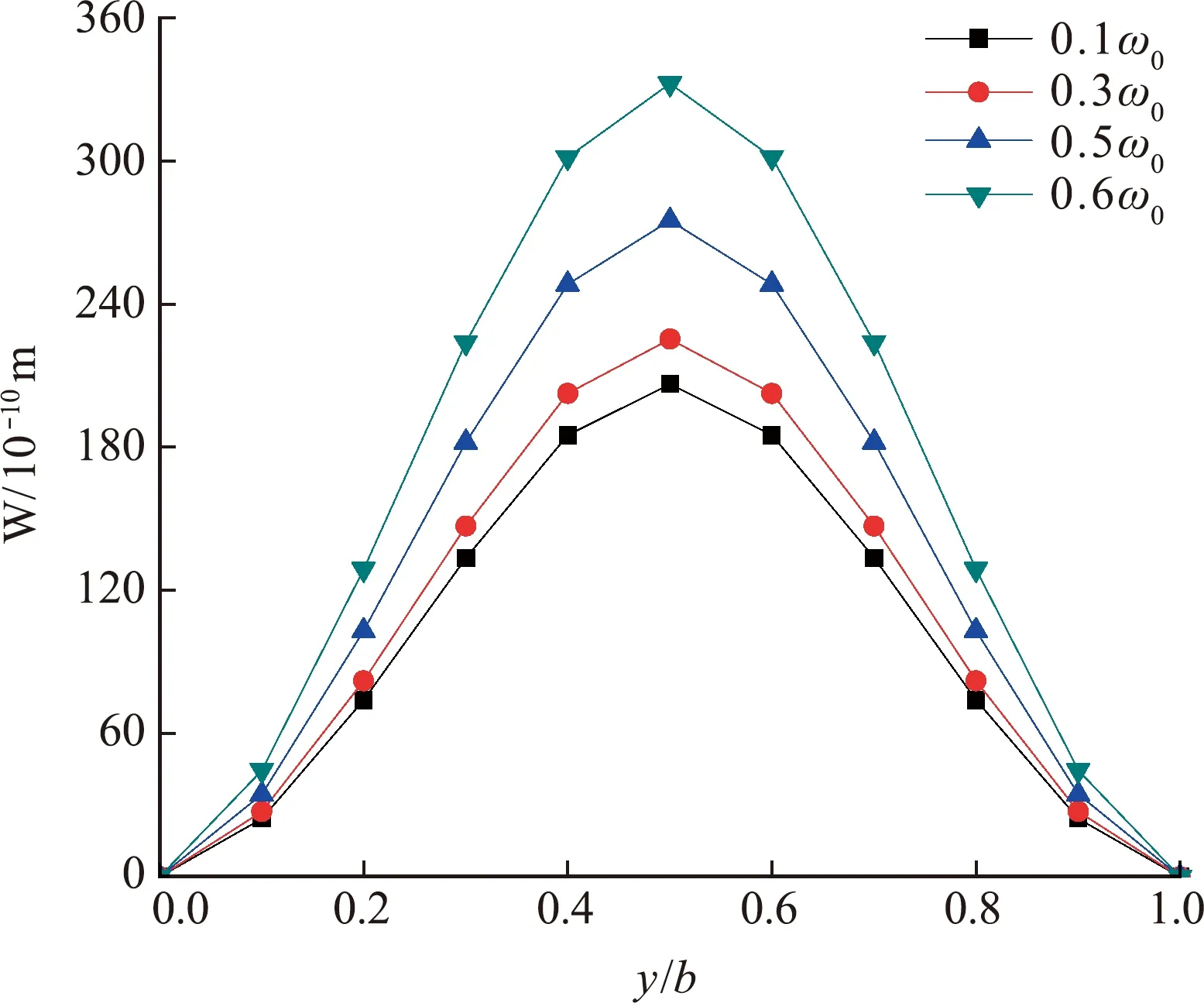
Fig.7 Method in this paper is used to calculate the deflection values of a forced vibration plate with four sides fixed (h /a =0.1,x /a =0.3)

Fig.8Methodinthispaperisusedtocalculatethedeflectionvaluesofaforcedvibrationplatewithfoursidesfixed(h /a =0.2,x /a =0.3)
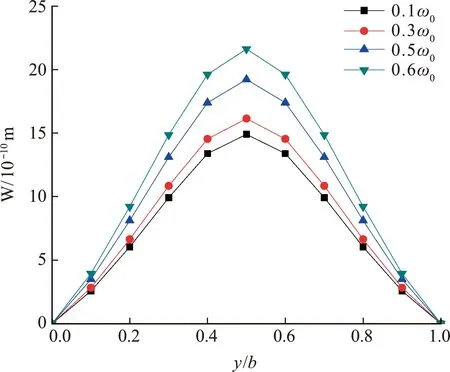
Fig.9Methodinthispaperisusedtocalculatethedeflectionvaluesofaforcedvibrationplatewithfoursidesfixed(h /a =0.3,x /a =0.3)
4 Result analysis
Forsimplysupportedthickrectangularplateswithfoursides,thecomparisonofthedatafromTables1to3showsthatwhenthefrequencyissmallandtheplatethicknessissmall,thedifferencebetweenthecalculationresultsofthispapermethodandthefiniteelementmethodissmall.Withtheincreaseofthicknessandvibrationfrequency,therelativeerrorincreases,buttheyarebasicallycontrolledwithin5%,whichhasacertainimpactontheerroroftheforceactingpointanditsnearbynodes.However,forthickrectangularplateswithtwooppositesidesfixedandtwooppositesidessimplysupported,itcanbeseenfromthecomparisonofdatainTab.4toTab.6thattherelativeerrorsarebasicallycontrolledwithin5%,andthereisalargeerrorattheactionpointofforceanditsadjacentnodes.
Inaddition,itcanbeseenfromFig.7toFig.9thatwhentheactionfrequencyissmall,theamplitudeofthethickplatechangeslittle.Withtheincreaseoffrequency,thevibrationamplitudeofthethickrectangularplateincreasessharply,whichisalsoinlinewiththebasiclawofvibration.
5 Conclusion
Solvingthethickplateproblemisultimatelyrequiredtosolveahigherorderdifferentialequation.Inthispaper,theboundaryintegralmethodissuccessfullyappliedtoavoidthisproblem,sothatitonlyneedsasimpleintegrationtoobtainthedeflectionsurfaceequationsoftheforcedvibrationofthickrectangularplates.ThroughnumericalcalculationonMatlabplatformandsimulationbyfiniteelementsoftware,itcanbeseenthattheboundaryintegralmethodisfeasibletosolvetheforcedvibrationproblemofthickrectangularplates,andthecalculationresultsinthispaperarecorrect.Therefore,itcanbedirectlyappliedtoengineeringpracticetosolvesomerelatedengineeringpracticalproblems.
