基于随动加载的起落架载荷误差评估与修正

王孟孟, 郑建军, 刘冰, 马远达, 王彬

(中国飞机强度研究所全尺寸飞机结构静力/疲劳航空科技重点实验室，西安 710065)

起落架是飞机起飞和着陆阶段安全性和可靠性的重要保障。因此，起落架连接区强度考核是新研飞机地面验证试验中重要和关键的考核项目之一[1]。验证试验中，通常在起落架轮轴点(作为起落架载荷施加点)施加载荷，考核起落架连接区域[2]。2010年前，国产小型飞机、军用战斗机研制较多，飞机起落架支柱刚度大，变形小[3]，地面验证试验中，撬杠加载技术[4-6]得到广泛应用，该技术具有加载稳定(压载转拉载)、飞机姿态易于控制、撬杠力臂调节灵活等优势。2010年后，国产大型、重型飞机广泛研制，由于减震、吸能、降噪等方面的需求，柔性起落架成为一种趋势[7]。起落架连接区强度考核时，柔性起落架受载变形，位于起落架上的载荷施加点随起落架变形发生位置改变，导致加载设备力线与理论载荷力线不重合，影响起落架加载准确性。面对上述问题，通常采用加载设备预置技术[8]，在试验前计算起落架轮轴点重点考核级(一般为最终载荷级)位移，按理论位移预置安装三方向加载设备。此方法操作简单，可以保证重点考核级载荷施加准确，但试验过程中存在较为明显的偏差。文献[9]采用增加固定撬杠的立柱高度，以此延长轮轴点到撬杠的力线距离，从而降低起落架变形后航向载荷、侧向载荷对垂向载荷的影响。文献[10]提出了针对撬杠加载的载荷修正，根据起落架变形后各方向加载设备力线与坐标系角度，重新分配施加载荷，在国产大型客机翼身组合体两点水平着陆静力试验中得到验证与应用。

2015年，中国飞机强度研究所科研人员提出了随动加载技术[11]，采用平面滚动轴承的结构形式设计平面随动机构，滚动钢珠以上部分钢板为移动板，钢珠以下部分钢板为固定板，作动筒筒体固定于移动板上，实现起落架垂向加载装置的随动加载功能。在水陆两栖飞机起落架静力试验[12]中使用了随动加载技术，消除了主起落架变形后垂向载荷对侧向和航向的影响。文献[8]起落架静强度试验中采用起落架随动加载技术、侧向与航向预置加载的混合加载形式，将加载误差控制在可接受范围内，提高了试验加载精度和试验效率。之后，以降低随动设备移动阻力、提高随动设备承载能力为目标开展了多轮研究。文献[13]介绍了一种基于双层滚柱平台的随动加载技术，通过计算及模拟试验对加载装置的承载能力及阻尼特性进行了验证，最终成功应用于某型号全尺寸飞机验证试验中。文献[14]介绍了一种起落架大载荷随动加载装置，通过随动框式传载结构与起落架假轮连接，框式结构下方平面安装滚动轴承实现低阻随动，下部环绕布置剪刀臂结构内置加载作动筒，剪刀臂结构保证了随动面的水平，可以提高试验加载能力及稳定性。文献[15]介绍了空客公司研制的一套飞机起落架加载装置，通过底板水平方向平动和转动模拟飞机起落架发生大变形后的侧向载荷、航向载荷以及自身的扭转矩，未介绍垂向载荷的施加。

综上所述，随着国产大飞机的蓬勃发展，起落架随动加载技术成为一种新兴主流加载技术。然而，随动加载技术是否依然存在误差、加载误差理论量值、误差如何修正等方面存在研究空白。为此，基于随动加载技术、加载设备预置技术，进行几何建模，通过理论分析推导随动加载误差计算公式和载荷修正公式，结合起落架典型工况进行载荷误差评估、修正和试验验证。

1 研究思路

1.1 误差来源分析

试验系统庞大且复杂，试验设备安装精度、控制系统参数、飞机姿态变化、试验扣重等均会影响试验加载准确度。对于飞机姿态变化，采用位移补偿技术得以保证，对于加载系统误差，通过适当调整控制参数不断优化，对于试验扣重和加载设备安装精度等通过预试结果分析并进行适当调整手段降低误差，对于起落架变形引起的误差，也是造成起落架加载误差的主要方面。

新兴的随动加载技术消除了垂向载荷对航向和侧向载荷的影响，由于航向及侧向加载设备自重、加载设备固定等因素未能实现随动加载，航向及侧向载荷分量对垂向载荷的影响未能消除，起落架变形后，随动加载模型如图1所示，可以看出，航向和侧向载荷相互产生载荷分量影响，同时在垂向也产生载荷分量，进而影响垂向载荷的准确施加。

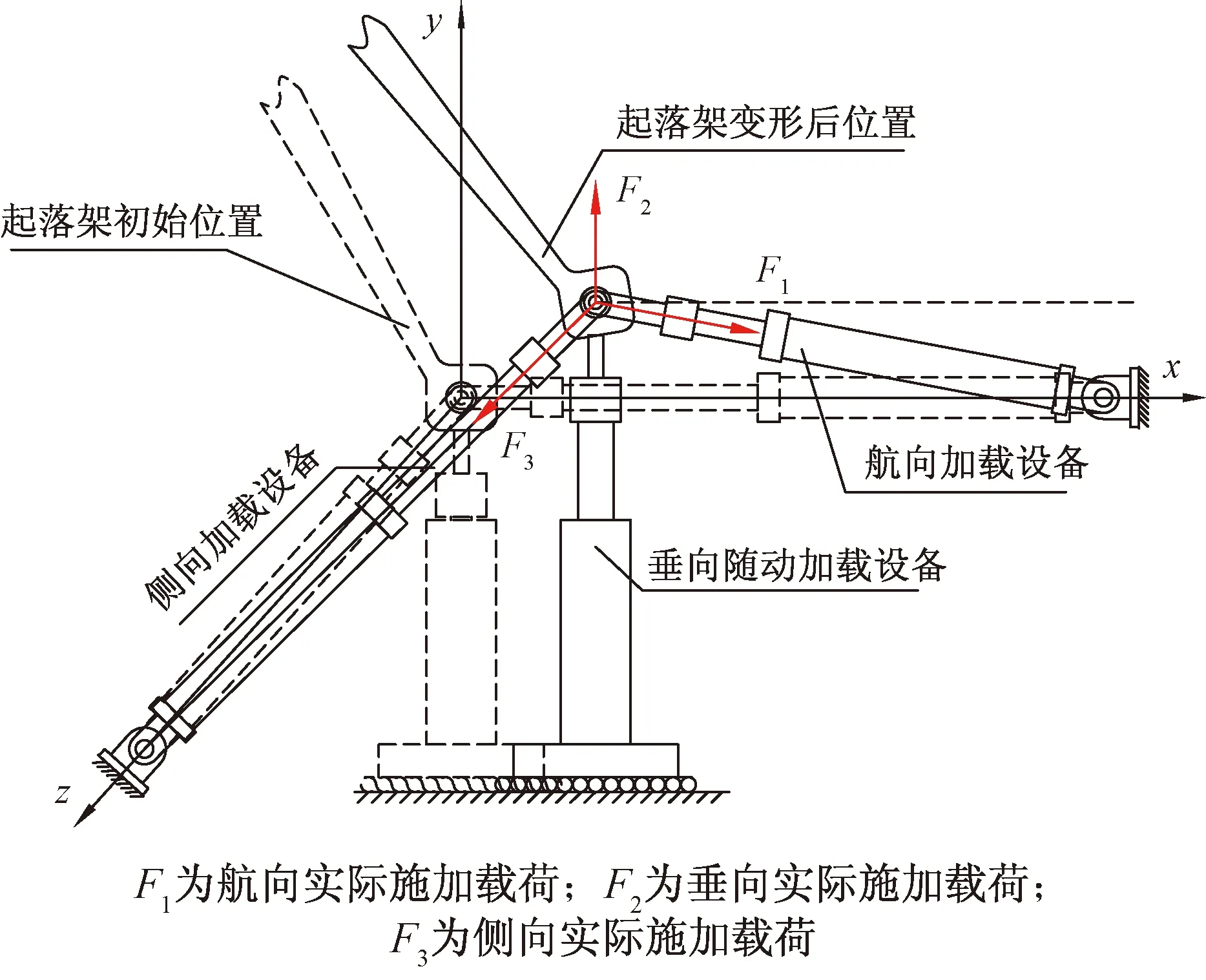
图1 起落架随动加载几何模型

1.2 研究方案

航向、侧向加载设备力线改变是导致加载误差的主要来源，随动加载技术结合加载设备预置技术在保证最终载荷准确施加的前提下，对试验过程中各级理论载荷进行矢量合成与分解[16]进而得到载荷误差，必要时进行载荷修正，方法流程如图2所示。

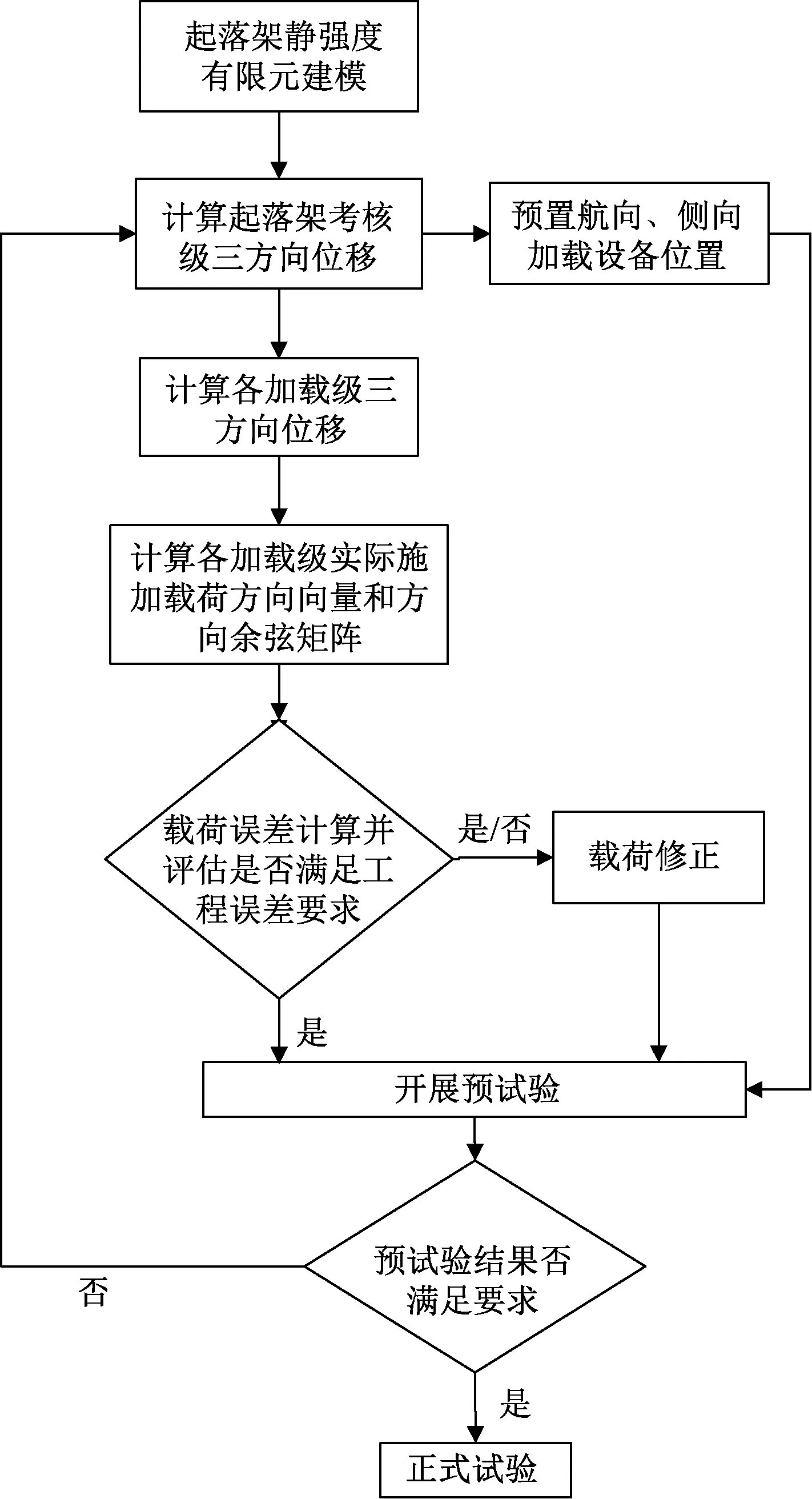
图2 方法流程图

依据图2流程思路，具体实现方案为：①采用有限元软件建立起落架加载模型；②计算起落架最终位移变形，作为航向、侧向加载设备预置安装位置；③建立随动加载几何模型，选取第i加载级为研究对象(静强度试验采用按级加载方法)，起落架轮轴点位移变形为xi、yi、zi；④通过几何关系得到三方向加载设备力线向量，整理后得到方向余弦矩阵；⑤计算各方向载荷误差，并评估误差是否满足工程要求；⑥若满足工程要求，则开展预试验；若不满足工程或进一步提升加载准确度要求，则建立力学方程，计算得到修正载荷后开展预试验；⑦开展预试验，通过约束反力误差进一步判断加载点误差是否满足要求；⑧如果预试验结果不满足要求，则从有限元计算开始查找原因并重新开展上述步骤；如果结果满足要求，则开展正式试验。

2 随动加载理论公式推导

起落架连接区强度考核试验中，设计专用起落架假轮，通过在假轮轮轴点附近设置各向连接孔位与加载设备进行连接，起落架随动加载示意图如图3所示。定义未变形时，起落架轮轴点为坐标原点，指向逆航向为x轴，垂直向上为y轴，z轴根据右手法则确定。计算得到最终起落架三方向变形量Δx、Δy、Δz，依此对航向设备，侧向设备进行预置安装，对其进行建模如图4所示。

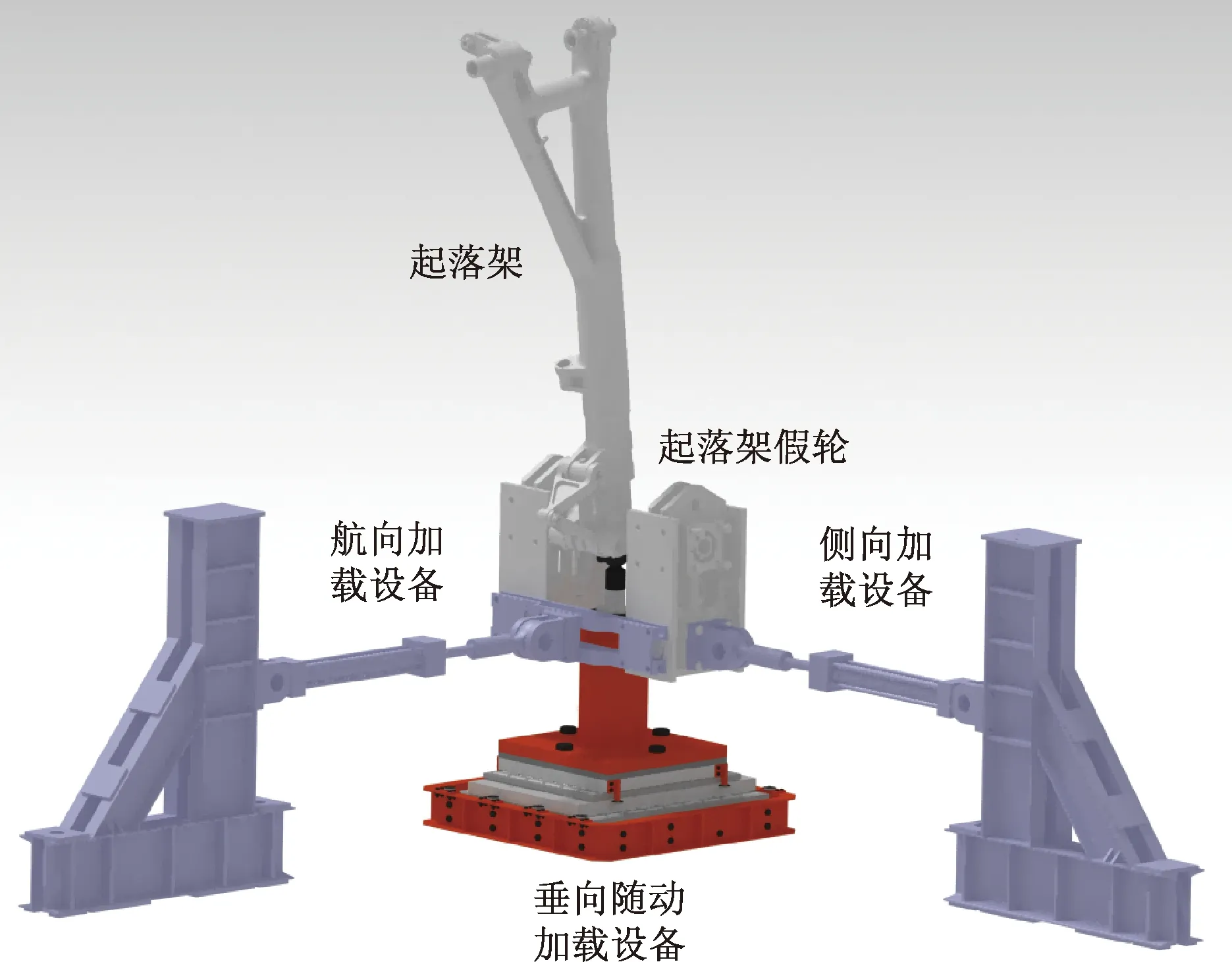
图3 起落架随动加载三维示意图

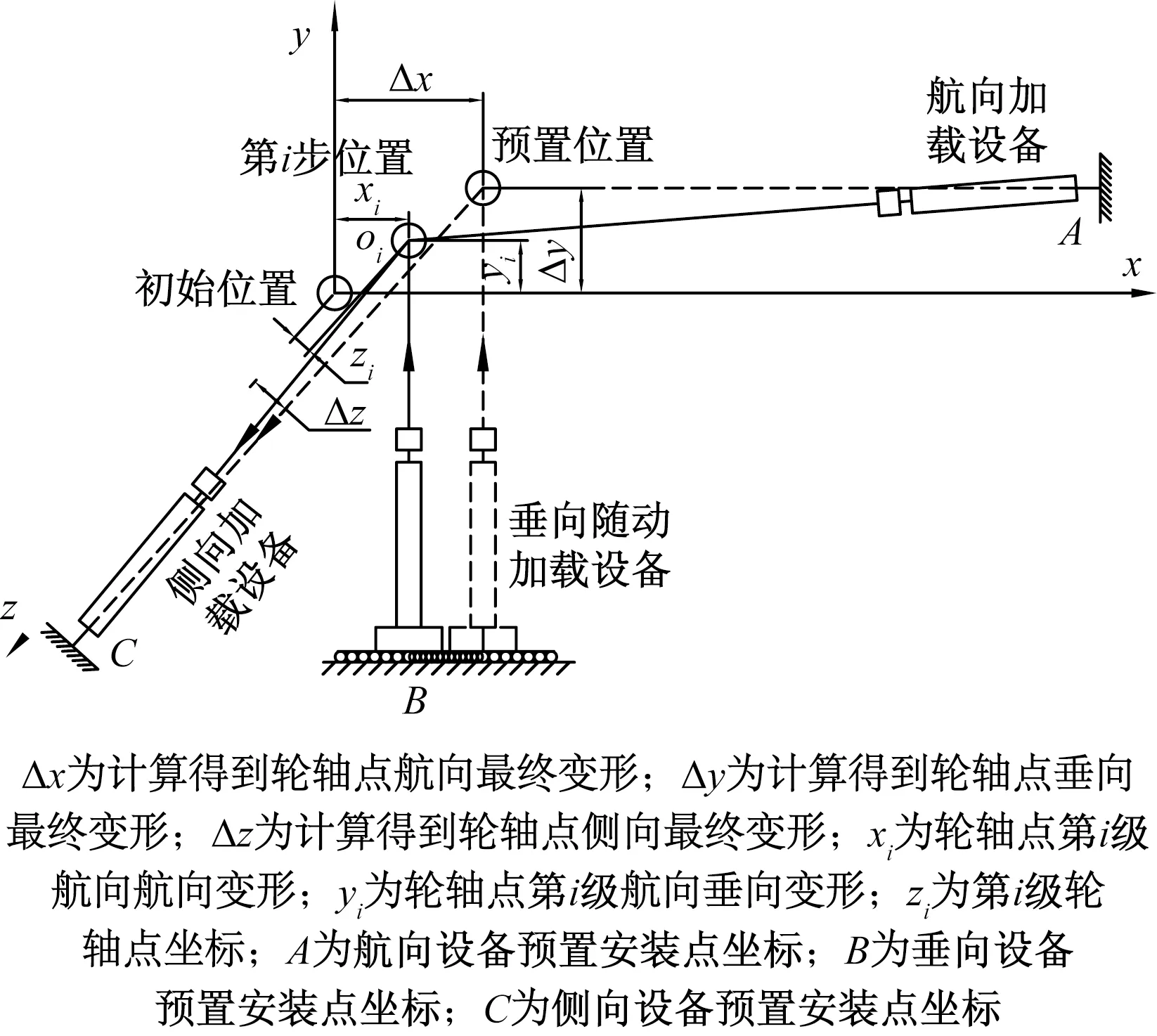
图4 设备预置后起落架随动加载模型

设备预置安装点坐标分别为A、B、C，给出各点坐标为

(1)

式(1)中：L1为航向加载设备固定位置与轮轴点初始位置的航向距离；L2为垂向随动加载设备底部与轮轴点初始位置的垂向距离；L3为侧向加载设备固定位置与轮轴点初始位置的侧向距离。

第i加载级，3个加载设备力线向量为

(2)

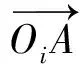
由于垂向使用了随动加载设备，xi-Δx、zi-Δz均为零，垂向加载设备力线向量为

(3)

将力线向量除以向量模，得到单位方向向量，即各加载设备力线与坐标轴夹角余弦值，矩阵形式为

(4)

式(4)中：加载至第i级时，αAi为航向加载设备力线与x轴夹角；βAi为航向加载设备力线与y轴夹角；φAi为航向加载设备力线与z轴夹角；αBi为垂向加载设备力线与x轴夹角；βBi为垂向加载设备力线与y轴夹角；φBi为垂向加载设备力线与z轴夹角；αCi为侧向加载设备力线与x轴夹角；βCi为侧向加载设备力线与y轴夹角；φCi为侧向加载设备力线与z轴夹角。

代入几何参数，求解得到方向余弦矩阵表达[式(5)]，各方向载荷误差计算公式为

(5)

式(5)中：

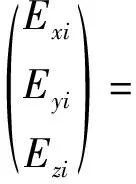
(6)

式(6)中：Exi、Eyi、Ezi分别为航向、垂向、测向载荷误差。

建立平衡方程[式(7)]，其中Fxi、Fyi、Fzi分别为第i加载级航向、垂向、侧向理论载荷，为已知量，F1i、F2i、F3i分别为航向、垂向、侧向修正载荷，为待求量，通过矩阵运算得到式(8)。

(7)

(8)

式(8)中：K11=cosβBicosφCi-cosφBicosβCi；K12=cosφAicosβCi-cosβAicosφCi；K13=cosβAicosφBi-cosφAicosβBi；K21=cosφBicosαCi-cosαBicosφCi；K22=cosαAicosφCi-cosφAicosαCi；K23=cosαBicosφAi-cosαAicosφBi；K31=cosαBicosβCi-cosαCicosβBi；K32=cosβAicosαCi-cosαAicosβCi；K33=cosαAicosβBi-cosβAicosαBi。

定义各向加载设备误差为

(9)

式(9)中：E1i、E2i、E3i分别为航向、垂向、测向加载点载荷误差。

方向载荷误差与加载设备误差也满足平衡方程[式(10)]。

(10)

3 误差评估与载荷修正

3.1 随动加载技术误差评估

以某大型全尺寸飞机静力试验起落架典型工况为研究对象。典型工况选取2BD2G0V(两点滑行刹车)，极限载荷(150%载荷级)单侧起落架最大航向载荷460.47 kN，垂向载荷578.37 kN，侧向载荷为0。根据有限元计算，极限载荷作用下起落架轮轴点航向位移变形280 mm，垂向位移变形54 mm，侧向位移变形87 mm。

取L1=2 500 mm，L3=2 000 mm，Δx=280 mm，Δy=54 mm，Δz=87 mm，xi=iΔx/150，yi=iΔy/150，zi=iΔz/150，将参数和理论载荷代入式(5)、式(6)，得到各加载级各方向载荷误差，计算结果如表1所示。

由表1可知，本典型工况三方向载荷误差整体呈现先增大后减小趋势，在150%载荷时误差为0，对各方向载荷误差进行分析与评估。

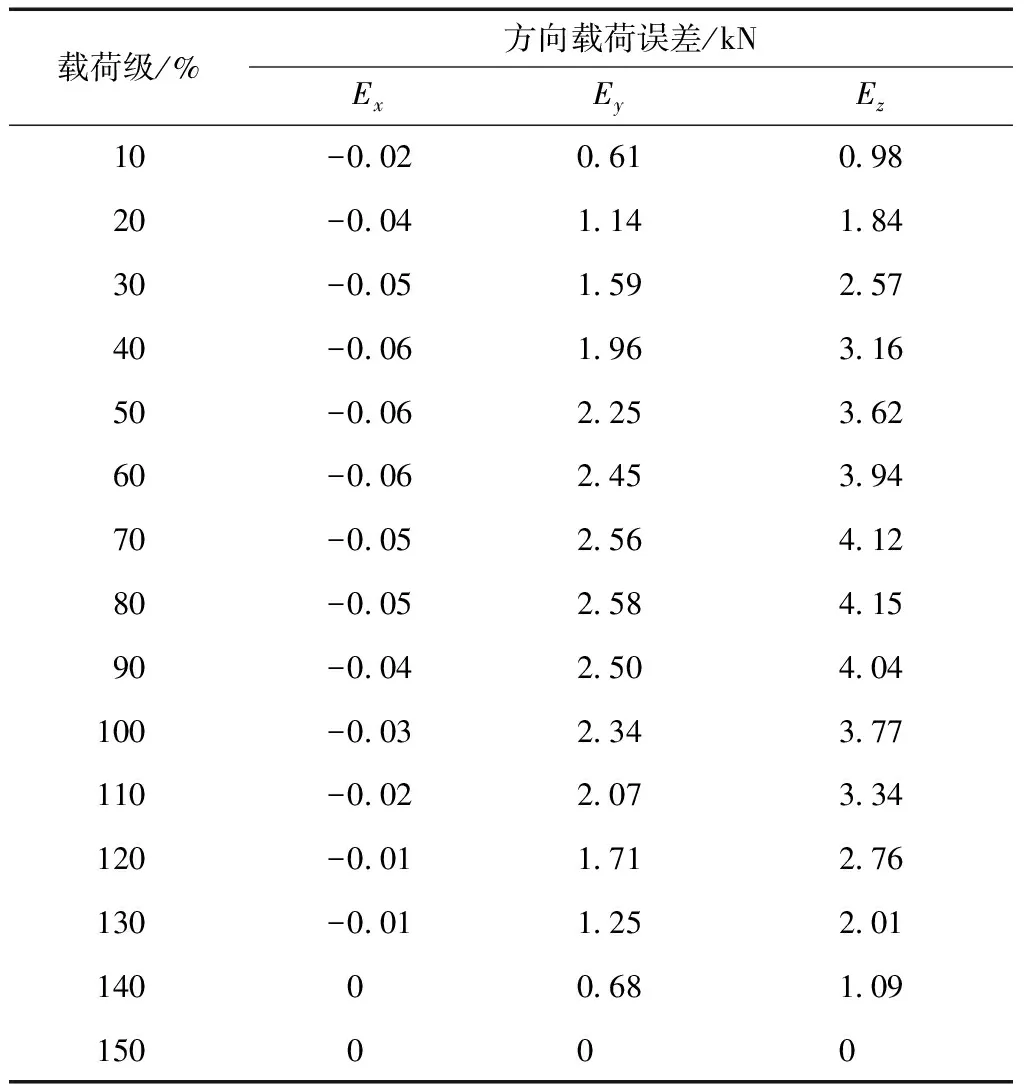
表1 各加载级各方向载荷误差

(1)由于起落架垂向和侧向变形，航向加载设备倾斜，航向载荷有所损失，航向载荷误差在50%载荷时达到最大，最大误差为-0.05 kN(负值表示欠载)，比例为0.09%，可以满足主动点1%工程误差要求。

(2)由于起落架垂向变形，航向加载设备产生垂向载荷分量，垂向载荷误差在80%载荷时达到最大，最大误差为2.58 kN(正值表示过载)，比例为0.36%，可以满足主动点1%工程误差要求。

(3)由于起落架侧向变形，试验过程航向加载设备产生侧向载荷分量，需进行起落架侧向载荷补偿，若不进行补偿，则由飞机约束点平衡，约束反力误差将最大增加4.17 kN，可以满足约束点5 kN的工程误差要求。

3.2 载荷修正

为了进一步减小误差，提升加载准确度，使用本文修正公式对载荷进行修正。将3.1节参数代入式(5)、式(8)，得到各加载级修正载荷，将理论载荷与修正后载荷对比如表2所示，对比曲线如图5所示。

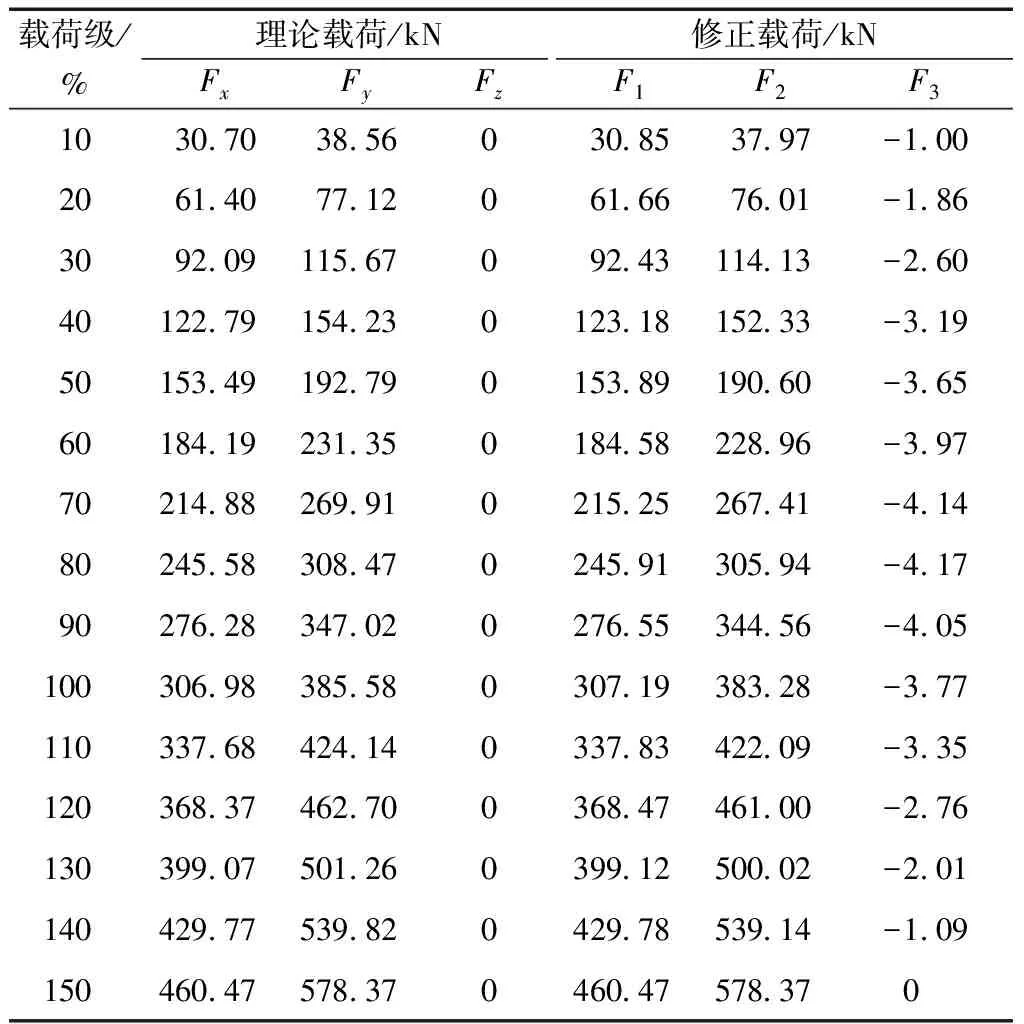
表2 理论载荷与修正载荷对比

由图5可知，在航向和垂向，理论载荷与修正载荷曲线重合度较好，侧向产生了附加载荷。

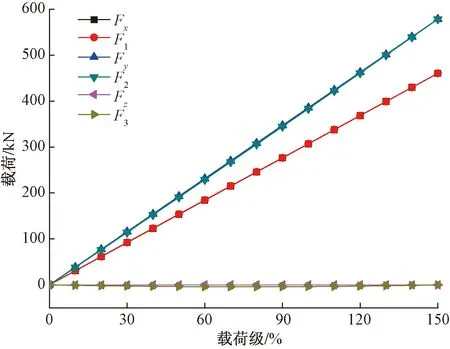
图5 理论载荷与修正载荷对比曲线

3.3 试验验证

为验证修正载荷的有效性和正确性，在某大型全尺寸飞机静力试验起落架典型工况2BD2G0V静强度试验中，采用了随动加载技术，加载部位为右主起落架，试验现场照片如图6所示。

图6 起落架随动加载试验现场照片

本试验采用了平尾垂向，左主起落架垂向和侧向，前起落架垂向、航向和侧向约束的空间6自由度静定约束方式，每个约束点安装测力传感器，通过观察约束点测力传感器反馈误差判断试验载荷施加是否准确。分别使用表2中理论载荷和修正载荷进行预试验，为充分验证本文修正方法，同时，防止高载荷作用下试验件结构产生有害残余变形，预试验最大加载至100%载荷级。本项试验航向和垂向约束反力误差区别不大，不进行讨论。左主起落架侧向约束与右主起落架侧向位置对称，可以直应反映右主起落架侧向载荷施加误差，分别记录两次试验左主起落架侧向约束误差，将其绘制成曲线，如图7所示。可以看出，在20%载荷之前由于结构扣重、加载设备载荷初值等因素的影响，实测值与理论误差差距较大；采用理论载荷预试验中，误差先增大后减小，全程未超过5 kN，可以满足试验要求，实测误差曲线与理论误差曲线趋势吻合良好，实测在70%载荷时误差达到最大，误差为4.4 kN，该加载级理论误差为4.12 kN，偏差为6.4%，理论误差最大出现在80%载荷，误差量值为4.15 kN，实测误差为4.2 kN，偏差为1.2%，根据误差计算公式得到的误差与实测误差量值接近；使用修正载荷进行试验，全过程(20%载荷后)误差小于2 kN，比理论载荷预试验过程中误差最大减小了3.3 kN。

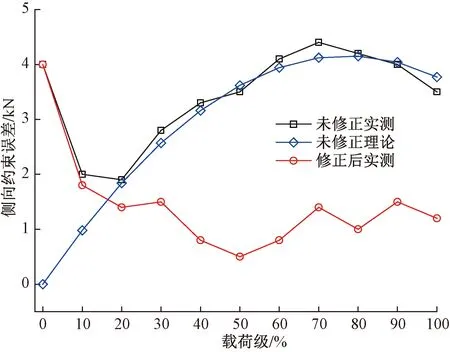
图7 侧向约束反力误差对比曲线

4 结论

基于垂向随动施加起落架载荷技术，分析其试验过程中理论上依然存在加载误差。通过建立模型推导得到误差计算公式。以某型飞机起落架典型工况为研究对象进行了误差评估与载荷修正，并进行了验证试验。得出如下结论。

(1)起落架随动加载技术可以消除垂向载荷对水平方向(航向和侧向)载荷的影响，水平方向载荷对垂向载荷影响较小，最大影响量值为0.62%。与传统起落架加载技术手段对比，随动加载技术(未修正)提高了起落架加载精度，误差量级比文献[10]中撬杠加载技术最大误差3.1%降低至0.36%。

(2)使用修正载荷进行试验，20%载荷后，约束反力误差小于2 kN，表明修正后的加载精度上得到了进一步提升，使起落架连接区考核更加充分。

(3)通过试验验证基于起落架随动加载技术的误差计算公式的正确性以及修正公式的有效性。可作为同类型试验过程中主动载荷和约束载荷误差分析的理论参考，为柔性起落架飞机地面验证试验更加准确考核起落架连接区静强度提供一种新的思路方法。