FOX-7 在有限温度下的热力学性质的理论计算

范俊宇，苏 艳，赵纪军

（1. 太原师范学院物理系，山西 晋中 030619；2. 太原师范学院计算物理与应用物理研究所，山西 晋中 030619；3. 大连理工大学三束材料改性教育部重点实验室，辽宁 大连 116024）

0 引言

含能材料是在没有外界物质参与下，受到外界作用时持续发生剧烈化学反应，并在短时间内释放出巨大能量的一类材料，已被广泛地应用于民用工业和军事领域［1-3］。含能材料在爆轰或爆燃过程中会经历高温高压等极端条件，并发生多次的结构转变［4-5］。因此，探索含能材料在极端条件下的反应行为，对理解其在高温和/或高压下的结构响应和基础物性至关重要。

1，1-二氨基-2，2-二硝基乙烯（FOX-7，C2H4N4O4）具有较高的热稳定性和优异的爆轰性能。在不同的温度和压力条件下，FOX-7 晶体具有多种晶型［6-9］，包括α，α′，β，γ和ε。常温常压下，α-FOX-7 晶体的分子排布呈波浪状单层，并通过分子间氢键和层间的范德华相互作用链接，构成具有P21/n空间群的单斜晶系［6］。温度加载下，FOX-7 晶体会先后发生α-β和β-γ相间的转变。其中，Kempa 和Herrmann［10］利用温度分辨的X射线衍射技术（XRD）研究了FOX-7 晶体随温度的相变行为，加热至113 ℃（386.15 K）时α相转变为正交的β相（空间群P212121），加热至173 ℃（446.15 K）转变为γ相。进一步，Evers 等［7］利用单晶XRD 也证实了FOX-7 晶体在116 ℃（389.15 K）时由α相至β相的转变。通过比对2 种相结构，发现2 个硝基基团强烈偏离由2 个碳原子和2 个氨基氮原子构成的分子平面，并发生分子层移动，使得α-和β-FOX-7 晶体内部形成不 同 的 氢 键 网 络。Crawford 等［8］利 用 单 晶XRD 和 差示扫描量热法证实了在446K 处β至γ相的转变，γ-FOX-7 可稳定存在于～435 K 直至其分解，将其淬火至200K 可确定为P21/n单斜晶系。

除了温度依赖的结构转变，大量的研究工作集中于FOX-7 的高压结构相变以及相关的物理性质［11-14］。而有限温度下的热力学性质却鲜有实验和理论报道。在原子分子尺度，含能材料的热力学性质与其晶体构型和分子堆垛密切相关，揭示其在外界加载下的变化规律有助于理解含能材料的结构响应［15-16］。例如，Yuan等［17］结合分子动力学和准简谐德拜模型研究RDX 的高压相变，发现α相到γ相的转变与其焓值的突变有关。Xue 等［18］利 用XRD 技 术 研 究 了 温 度 依 赖 的HMX 相变，指出在β相转变为δ相前，其c轴的热膨胀系数随着温度的升高而收缩。在介观和宏观尺度，含能材料的理论模拟常用于研究燃烧、热点形成等物理机制［19-20］，而这一尺度的理论建模迫切需要体系的热力学性质作为输入参数。此外，色散修正的密度泛函理论可用于描述常压和高压下含能材料的结构与物性［21］，但无法对温度加载下的结构特征和热物理量准确计算。

为此，本研究将采用准简谐近似结合色散修正的密度泛函理论来评估FOX-7 在有限温度下（即绝对零度至熔化/分解温度～500 K）的结构和热力学性质。其中，计算的晶胞体积和晶格参数与文献实验测量值符合较好，表明当前计算方法能够合理地评估FOX-7 中的分子间相互作用。通过与现有实验数据的比对，阐明温度加载下FOX-7 的结构参数（晶格参数、热膨胀系数）与分子构型之间的关联，进一步揭示不同条件下FOX-7 晶体基础热力学性质（热容、熵、体积模量等）的演化规律，这些热力学参数不仅有助于构建准确的热力学模型，也为介观和宏观尺度模拟提供了关键的输入参数。

1 计算方法

所有的密度泛函理论计算均采用CRYSTAL17 程序包来完成［22］。计算采用全电子的6-311G（d，p）基组，选取广义梯度近似下的Perdew-Burke-Ernzerhof（PBE）泛函用于处理体系的交换关联相互作用［23］。采用Grimme 提出的DFT-D3 半经验色散校正方案处理FOX-7中的分子间相互作用［24］。Monkhorst-Packk点［25］网格密度设置为0.05 Å-1，用于布里渊区的采样。晶格参数和原子坐标利用Broyden-Fletcher-Goldfrab-Shanno（BFGS）算法充分优化［26］。

准简谐近似下，亥姆霍兹自由能F（T，V）可表达为：

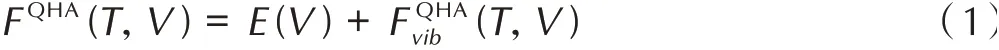
式中，E（V）为系统基态的内能，eV，Fvib（T，V）为与体积相关的总振动自由能，eV。

包含零点能和温度相关分量如式（2）：式中，EZPE为零点能，eV，kB为玻尔兹曼常量，ℏ 为约化普朗克常量，wk，p为声子频率，cm-1，取决于晶胞体积，给定温度下的平衡体积V（T）则通过最小化FQHA（T，V）来获得的，晶格参数和原子坐标则在给定的体积下进行弛豫。

晶体的热力学性质需要计算第一布里渊区的声子频率。基于实空间的冷冻声子方法，仅计算FOX-7 晶体（包含56 个原子）在Γ点的声子频率，计算的频率对应于倒空间中第一布里渊区中Γ点的声子色散采样。基于标准统计力学中的振动分布函数可获得简谐热力学量，进一步应用准简谐近似来修正简谐近似与实验值的误差。具体而言，我们选择了4 个体积，即-3%、0%、3%、6%，并在每个约束体积下进行几何优化。对于每个优化的结构，计算声子频率并估算出振动自由能。进一步根据公式（1）和（2），可获得给定温度下的亥姆霍兹自由能FQHA（T，V）。

此外，体积热膨胀系数αV（T），K-1定义为：

其中，与模式相关的格林乃森参数定义为：

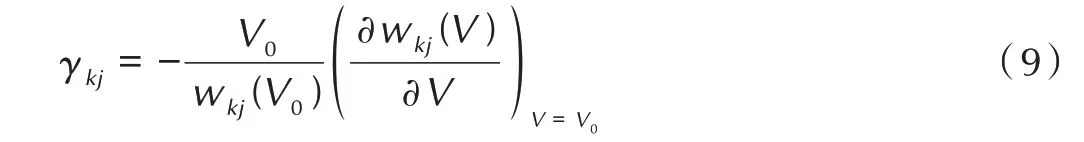
2 结果与讨论

2.1 实验温度下FOX-7 的晶格参数

目前，色散修正的密度泛函理论能够有效评估分子间的弱相互作用，已被广泛应用于含能材料的晶体结构、分子间相互作用和物性研究［27-29］。本研究基于色散校正的密度泛函理论，考虑零点能和温度效应修正来评估FOX-7的结构参数以及分子间的非键相互作用。

常压下，FOX-7 晶体是空间群为P21/n的单斜晶系，其晶体结构和分子构型如图1 所示。基于色散修正的密度泛函理论，计算了FOX-7 晶体考虑零点能和温度效应修正后的晶格参数，如表1 所示。相比于实验值［6］，0 K 下，FOX-7 晶胞体积的计算值比实验值低3.53%，这部分误差主要来源于半经验的DFT-D 色散校正方案高估了FOX-7 的晶格能（即分子间相互作用），从而低估了晶格参数。通过加入零点能修正，FOX-7 的晶胞体积与实验值的误差下降至-1.65%，这意味着零点能效应在确定FOX-7 晶体结构中起着重要作用。进一步，将零点能和温度效应都纳入色散校正DFT 方案，此时，FOX-7 的晶胞体积与实验值的偏差仅为-0.39%，且实验温度下（173 K）晶格参数的计算值与实验值的误差均在1%以内。这些计算结果表明，引入零点能和温度效应可以有效评估温度加载下含能材料的分子间相互作用和结构参数，显著提升当前计算方案的适用性。

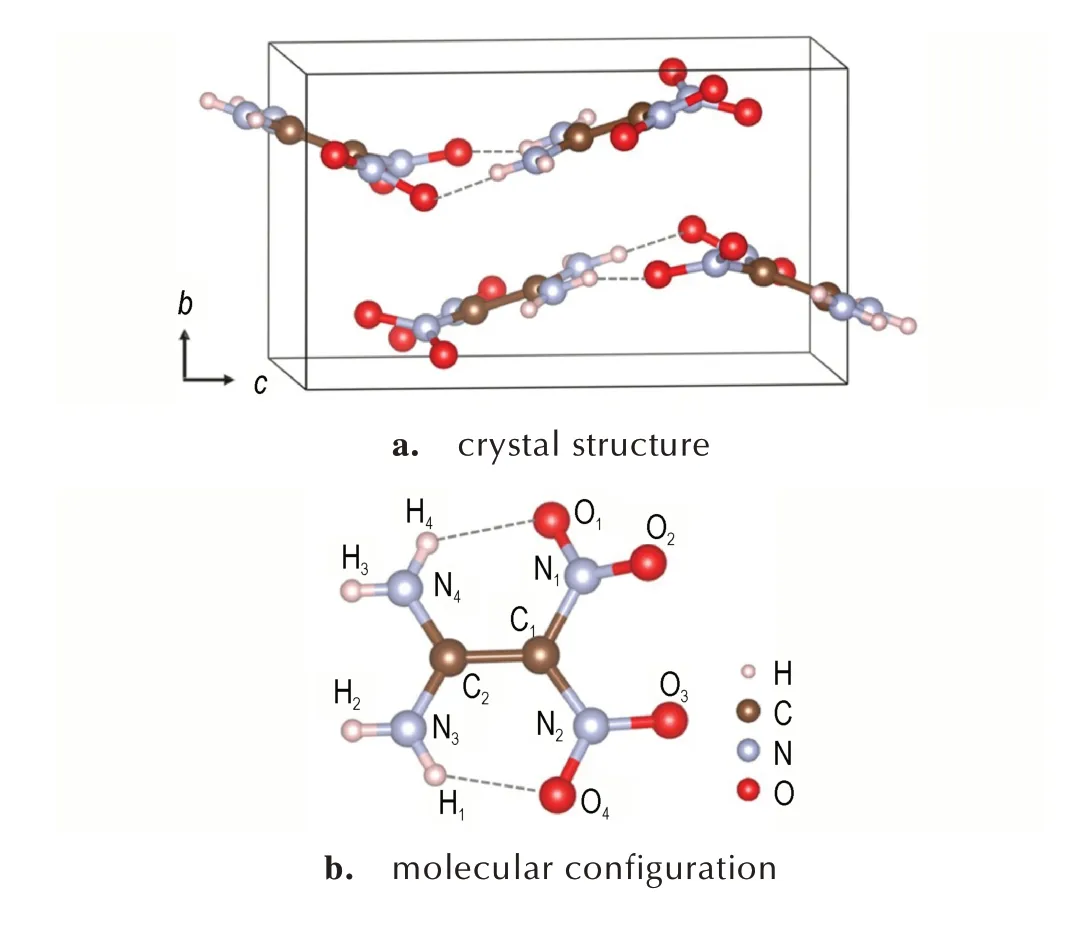
图1 常压下FOX-7 晶体的结构与分子构型Fig. 1 Crystal structure and molecular configuration of FOX-7 at ambient condition

表1 包含零点能和温度修正的FOX-7 晶体的晶格参数与实验值（173 K）的比较Table 1 Comparison of lattice parameters and experiment values（173 K） of FOX-7 including zero-point energy and temperature corrections

2.2 有限温度下FOX-7 的晶格参数及其演化规律

相比于等温状态方程，等压状态方程对于大规模连续介质模拟同等重要，但实验和理论数据相对匮乏。因此，我们计算了0～500 K 范围内FOX-7 晶体的等压状态方程来考察其温度依赖的结构性质。有限温度下FOX-7 的晶胞体积变化如图2a 所示。在0～50 K时，FOX-7 晶体的晶胞体积缓慢增大，随着温度的进一步升高，晶胞体积几乎呈线性关系增长。相比于文献实验测量结果［7］，计算的体积变化斜率总是小于实验测量的斜率，这一误差主要源于当前的准简谐近似未考虑固有的非谐声子-声子相互作用。此外，在温度低于300 K 时，计算的FOX-7 晶胞体积高于实验值。由于在给定温度下的平衡体积V通过最小化FQHA（T，V）来获得，因此，当前的计算方案将可能高估低温下振动自由能的贡献。

相比于晶胞体积随温度的演化，FOX-7 的晶格参数在0～500 K 的温度范围内几乎呈线性增长，正如图2b 所示。计算的晶格参数随温度的演化与实验数据符合较好［7］，尤其在晶轴a和c方向。当温度超过300 K 后，由于当前的计算方案对层间方向的非键相互作用描述不够充分，导致计算的晶格参数b与实验值有明显的误差。此外，不同方向晶格参数对温度的依赖性也反映了FOX-7 晶体显著的各向异性，其中，b轴方向晶格参数随温度变化的斜率大于a和c轴方向，表明FOX-7 晶体沿着层间方向更易发生膨胀。

晶体的热膨胀系数与晶体类型和分子构型密切相关，能够反映含能分子晶体显著的各向异性。因此，我们计算了FOX-7 晶体在0～500 K 温度范围内的热膨胀系数。图3a 和3b 分别给出FOX-7 晶体体积和晶格的热膨胀系数随温度的变化。其中，FOX-7 的体积热膨胀系数在低于200 K 时呈指数增长，这一较大的增长率主要来源于晶格参数b。正如前文所述，FOX-7的晶体结构是通过逐层堆叠形成的，呈现大量的层内和层间氢键网络，而沿着b轴方向，分子层之间弱的非键相互作用导致晶体更容易受热膨胀。

图3 FOX-7 晶体在有限温度下的热膨胀系数Fig.3 Thermal expansion coefficients of FOX-7 at the finite temperature

值得注意的是，当温度超过200 K，FOX-7 的热膨胀系数的增加变缓甚至收缩，直至熔化/分解温度。这一现象表明在该温度阶段，FOX-7 晶体的热膨胀受到限制，可能会影响其晶体结构以及分子构型随温度的变化。进一步，我们选取不同的温度点来考察FOX-7晶体中分子构型和氢键的变化。图4 绘制了FOX-7 晶体中分子的结构参数以及分子间-和分子内氢键键长随温度的演化。由于氨基基团与C—C 键构成FOX-7分子平面（图1），从图4a 可以看到，NO2基团与分子平面所构成的二面角呈不连续变化，且转折点发生在200 K 附近；而FOX-7 的分子键长（包括C—C 键和C—N 键）随温度的上升几乎呈线性增加，如图4b 所示。在图4c 中，所有的分子间氢键（N—O…H）随温度的增大而伸长，而分子内氢键长基本保持不变。这一结果表明温度升高导致FOX-7 中的分子间相互作用逐渐减弱。值得注意的是，在温度达到200K 时，分子间氢键存在不连续变化，即FOX-7 晶体中的分子间相互作用发生突变。而这一变化引起FOX-7 分子中NO2基团的旋转，并导致其热膨胀系数在200K 附近发生收缩。FOX-7 的X 射线衍射实验［7］表明FOX-7 晶体发生α至β相 转 变 时，FOX-7 分 子 的NO2基 团 与 分 子 平面发生较大的旋转，当前的计算结果与实验测量值保持一致。因此，有限温度下-NO2的旋转和热膨胀系数的收缩可能是FOX-7 相结构转变的重要步骤，而分子间相互作用的突变可能引发FOX-7 的潜在相变。

图4 FOX-7 晶体中NO2基团与分子平面的扭转角、分子键长和氢键随温度的变化Fig.4 Change of the torsion angles，bond lengths and hydrogen bonds between the NO2 group and the molecular plane of FOX-7 with the finite temperature

此外，我们拟合了分子键长与温度的线性系数，发现C— NO2键 长 随 温 度 增 长 的 斜 率（3.23×10-5，3.14×10-5Å/K）略 高 于 其 他C— N 键（2.62×10-5，2.97×10-5Å/K）和C—C 键（3.02×10-5Å/K）。同时，FOX-7 的热分解实验表明C—NO2键是FOX-7 晶体分解反应的触发键，且C—NO2键的均裂可能是分解过程中的重要步骤［9，11］。因此，相比于其他分子键，C—NO2键更容易受热伸长而降低键的强度，在温度加载下更加敏感。

2.3 与温度相关的热力学性质

含能材料的基础热力学性质不仅可以为介观或宏观尺度的热力学模拟提供关键参数，也能为理解含能材料在温度加载下的响应提供理论依据。其中，分子晶体的体积模量可以通过状态方程来确定，是评估材料刚度的重要参数。因此，我们计算得到了在有限温度下FOX-7 的体积模量随温度演化的曲线，结果如图5 所示。由图5 可以看出，在等温（Bt）和绝热（Bs）条件下，FOX-7 晶体的体模量随温度升高而降低，表现出明显的温度依赖性。通常实验值是在绝热条件下测量的，例如室温（300 K）下，实验报道FOX-7 的体积模量是17.6 GPa［14］，本研究计算的绝热体积模量为15.88 GPa，误差为-9.77%。由于体积模量的确定与压力传递介质的类型、拟合范围和拟合方法等都有关，因此，当前计算的体积模量相对合理。

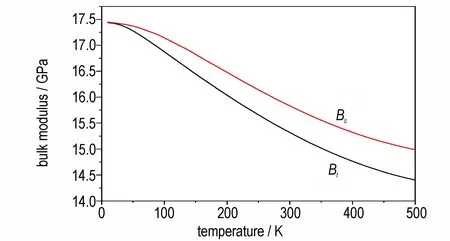
图5 等温（Bt）和绝热（Bs）条件下FOX-7 晶体的计算体模量随温度变化的曲线Fig.5 Change curves of calculated bulk modulus of FOX-7 crystal with temperature at the isothermal（Bt）and adiabatic（Bs）conditions

通常基于简谐近似，一些基本的热力学参数（如等容热容和熵等）可以直接通过声子频率获得。实验测量热容往往在等压条件下进行，故本研究计算了等容和等压条件下FOX-7 晶体的热容随温度的变化，结果如图6a 所示。在低温时，等容热容和等压热容表现出相近的数值和变化趋势，而随着温度的升高，两种条件下的热容产生明显差异，如温度达到500 K 时，两者相差18 J·mol-1·K-1。因此，对于具有较大热膨胀系数的分子晶体，等容条件和等压条件下获得的热力学参数会存在明显差异。图6b 绘制了等容和等压条件下熵随温度的变化曲线。2 种条件下计算的熵随温度的升高而增大，温度达到500 K 时，两者相差35 J·mol-1·K-1。通常，材料的熵在实验上通常难以直接测量，这些数据可为实验测量提供有用的参考。此外，格林乃森参数γ（T）量化了声子模式的变化，是对声子模式非谐性的量度，且与三阶力常数直接相关。在给定温度下，计算的格林乃森参数如表2 所示，其值随着温度的升高而减小，表明FOX-7 晶体中的非谐作用随温度的升高而减弱。这些数据可为FOX-7 的宏观和介观理论模拟提供关键输入参数。

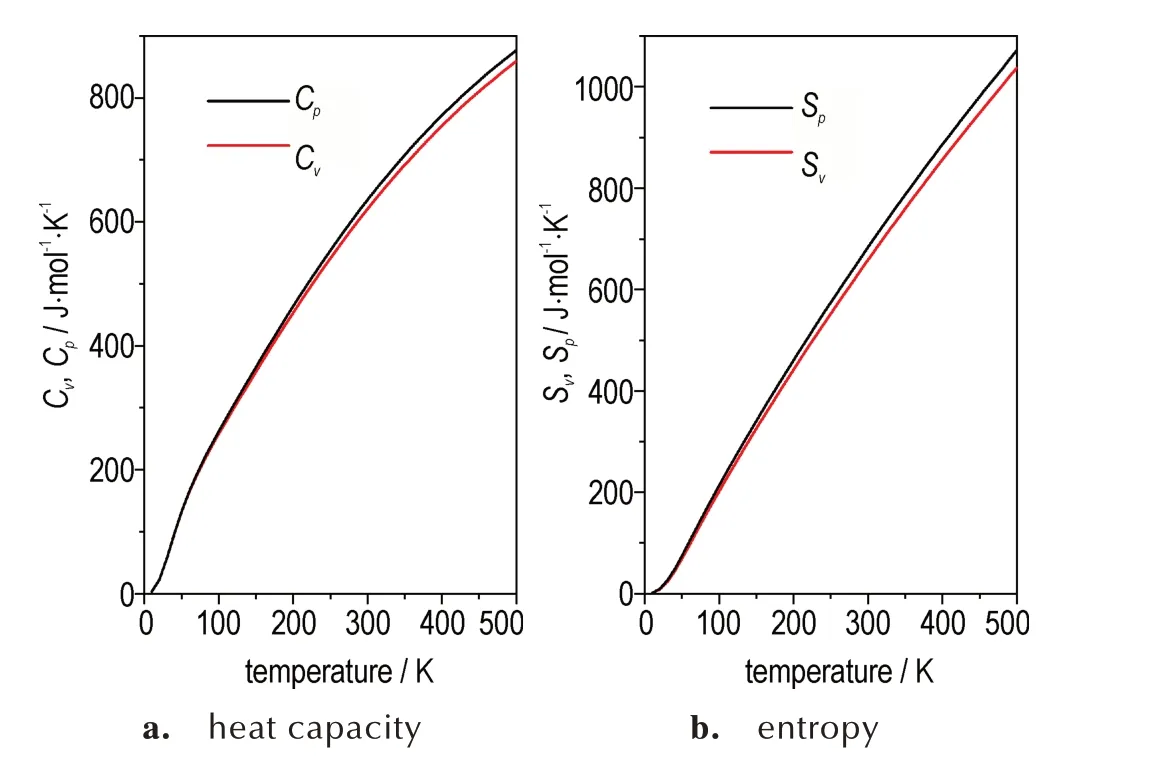
图6 等压（P）和等容（V）条件下，FOX-7 晶体热容和熵随温度的变化Fig.6 Change of Heat capacity and entropy of FOX-7 crystal with temperature under the constant volume and pressure

表2 给定温度下FOX-7 晶体的格林乃森参数Table 2 Calculated values of Grüneisen parameter（γ）of FOX-7 at the given temperature

3 结论

（1）色散修正的密度泛函理论，结合零点能和温度效应修正方案可以有效描述FOX-7 晶体在有限温度下的结构参数和热力学性质。实验温度下（173 K）晶格参数的计算值与实验值的误差在1%以内，表明零点能和温度修正的引入可显著提高计算的准确性。

（2）在0～500 K 温度范围内，FOX-7 晶格参数的计算值与实验值基本一致。由于声子间相互作用的缺失，计算所得晶胞体积的斜率略低于实验值。此外，FOX-7 晶体的热膨胀系数表现出显著的各向异性，即层间方向（b轴）的热膨胀系数远大于层内方向（a轴和c轴）。

（3）通过结构分析发现，FOX-7 热膨胀系数在200 K 附近的收缩现象与NO2基团的旋转有关。NO2基团与FOX-7 平面所成的二面角在200 K 时发生突变，这一变化使得体系内部的分子间相互作用发生变化，从而可能诱发FOX-7 晶体的潜在相变。

（4）基于准简谐近似，预测了FOX-7 晶体的基础热力学参数。室温、绝热条件下计算的体积模量（15.88 GPa）与实验值（17.6 GPa）比较相对合理，且体积模量随温度的演化反映了FOX-7 在有限温度下的软化行为。等容和等压条件下的热容和熵均随温度的升高而增大，且高温下2 种条件下计算的热容和熵受非谐作用影响表现出明显的差异，如温度达到500 K时，等容和等压条件下的热容相差18 J·mol-1·K-1，熵相差35 J·mol-1·K-1。这些数据可以为FOX-7 的宏观和介观理论模拟提供关键的输入参数，也为实验测量提供有用的参考。