基于密度分类的JPS+移动机器人全局路径规划算法

林彬彬， 韩宝玲*， 许仕杰， 陈禹含

(1.北京理工大学机械与车辆学院， 北京 100081； 2.北京理工大学机电学院， 北京 100081)

近年来，随着科学技术的飞速发展，自主移动机器人逐渐进入了社会应用领域，在社会的各方各面发挥着重要作用。自主移动机器人可以通过一些传感器实现自主运动，进而代替或协助人类完成一些操作和任务。全局路径规划是移动机器人完成导航等任务的前提条件。全局路径规划是通过机器人携带的传感器对于周围环境的静态障碍物进行感知，建立静态地图后，给定起点和目标点，再根据已知地图找到一条从起点到终点的无碰撞路径[1]。常见的全局路径规划算法有Dijkstra算法[2]、A*算法[3-4]、概率路线图(probabilistic road map, PRM)方法和快速搜索随机树(rapidly-exploring random tree, RRT)算法[5-6]。

Dijkstra算法是最典型的最短路径算法，但存在访问节点数量多、效率低下等问题；A*算法加入了与终点相关的启发式函数，实现了对于环境的快速响应，能够直接搜索路径，因此在移动机器人中得到了广泛应用。但使用A*算法搜索时，实时性较差，且访问列表节点产生的计算量与内存开销增加了计算时长。因此，针对A*算法的不足，Harbor等[7]提出了跳点搜索算法(jump point search, JPS)。JPS算法对于访问的邻居节点和列表节点重新定义了规则，提出了"强制邻居"和“跳点”的定义，剔除搜索过程中的无意义的节点，只留下特殊的节点，即提出的跳点，将这些跳点连接起来就可以得到完整的全局路径。赵晓等[8]将JPS算法应用于移动机器人的路径规划，证明了JPS算法优于A*算法；宋晓茹等[9]对于节点扩展策略进行了改进，魏博闻等[10]和Zheng等[11]对于节点扩展策略和启发式函数做了修改，进一步提高了JPS算法的时间效率。但在大比例尺的地图中，JPS计算关键节点的递归层数多，时间开销非常大，使得计算时间长，针对此问题，Harbor等[12]提出了JPS+算法，将全局路径规划的效率再一次提高。

针对JPS+算法的跳点识别的策略，Iakushkin等[13]提出了一种将障碍物根据相邻关系识别为不规则多边形，并将多边形的角点作为跳点，这样做减少了点的访问数量；Jiang等[14]提出了一种双向JPS+算法，提升了路径的安全性。但该算法仍存在地图中主要跳点的设置不合理与时间效率的提高问题。

针对上述问题，提出了一种JPS+的改进算法，目标是在保证寻路有效性的条件下实现更少的主要跳点的识别，同时在路径搜索过程中改进中间点的识别规则，提高算法的时间效率。

1 JPS+算法

JPS+算法是在JPS算法的基础上，对于跳点规则进行修改，得到了带有方向性质的跳点，后根据跳点的情况对整个地图中的点进行预处理，使寻路速度更快。

1.1 跳点识别规则

1.1.1 强制邻居

识别并选择扩展某些特定的关键节点，在生成路径时，既保证了路径准确性又减少了节点的访问数量的节点，被称为跳点。为了能更好地识别出跳点，JPS算法定义了“强制邻居”，“强制邻居”与常规的邻居节点的区别在于考虑了障碍物的出现与分布情况。

在图1中展示了出现“强制邻居”的两种情况。定义当前搜索的节点为x，其父节点为p(x)，搜索的节点为n，直接从p(x)到达节点n的路径长度为l1，从p(x)经过节点x，再到达节点n的路径长度为l2。当障碍致使l1>l2时，节点n称之为“强制邻居”。当p(x)到x为直线运动时，因为障碍物的存在导致斜线运动必须通过节点x才可以实现[图1(a)]；当p(x)到x为斜线运动时，因为障碍物的存在导致p(x)到节点n之间的直接到达不能实现[图1(b)]。具体来说就是图1(a)中的节点9与图1(b)中的节点1。

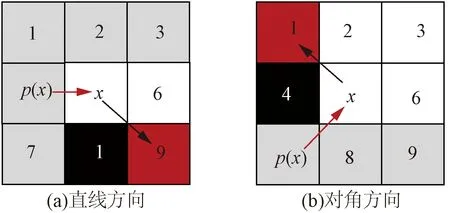
图1 强制邻居示意图Fig.1 Diagram of forced neighbor

1.1.2 跳点识别

因为JPS+需要进行地图的预处理，离线记录各节点周围的障碍物或跳点信息，因此需要事先找出地图中的所有带有“强制邻居”的点。因此制定了如图2所示的跳点的识别规则对于跳点进行基本方向的判断。图中的p(x)是访问节点的父节点，x是当前访问的节点，虚线框表示的是“强制邻居”，因此图中的x就表示是从p(x)到x方向上的跳点。

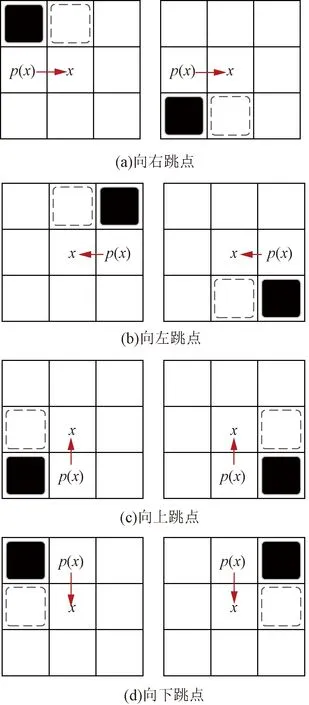
图2 JPS+跳点识别规则Fig.2 Jump point identification rules of JPS+

JPS+算法的跳点识别方式需要对于每一个栅格点进行遍历，并且对于周围8个栅格状态进行判断得到，导致搜索效率低下。因此可以针对跳点与障碍物点之间的联系开展进一步的分析，抛弃以可行空间为主导的跳点识别思路，转换到以障碍物的分布为主要判断依据的方式，进而避免遍历过程，提高处理效率。

1.2 地图预处理

地图预处理的目的是实现对于地图的附加信息的获取。对于每个栅格点，可以前进的方向均有8个，用一个矩阵将这八个方向可以前进的距离记录下来，通过对于预处理完成各方向前进距离的计算，可以更高效地找到当前点的可行方向与可到达的位置。

预处理分为以下四步：

(1)识别主要跳点。根据原始JPS+算法的识别方式完成对于主要跳点的识别，如图3所示中的带有灰色圆圈的即为主要跳点。

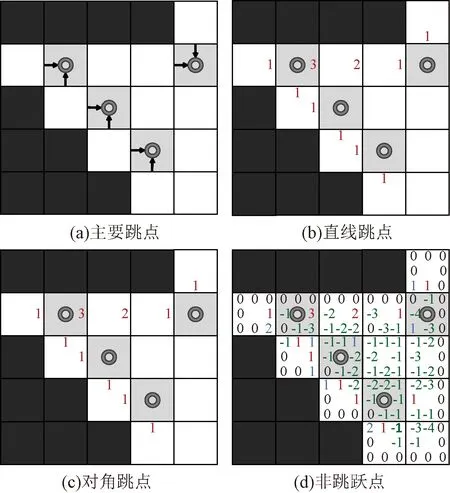
图3 地图预处理过程Fig.3 Map preprocessing

(2)识别直线跳点。沿水平或竖直方向可以无障碍到达主要跳点的栅格点，通过直线方向遍历获得，用正数表示与主要跳点距离。

(3)识别对角跳点。确定直线跳点后，沿对角线方向可以无障碍到达主要跳点或直线跳点的栅格点方向，通过对角线方向遍历得到。

(4)非跳跃点处理。不满足能够达到跳点的栅格点，用负号表示不可达，数字表示距离。

如图3所示地图所有方向处理。

地图预处理的过程能够保证每个栅格点位置都能够包含周围障碍物的关键信息，在处理静态地图的情况下，可以重复利用地图预处理的信息，对于地图的利用效率极高，因此在全局路径规划过程中具有较强的实用性。

完成地图预处理后，算法通过A*的方式进行路径的搜索，根据预处理后保留的周围环境信息，只针对跳点进行节点扩展。同时因为预处理过程不会将目标点处理为特殊节点，需要判断当前节点是否能够直接到达目标点，针对当前判断准则会保留不满足条件的冗余节点的问题，提出的改进算法也进行了判断条件的更新，删除冗余节点，进一步提高搜索效率。

2 改进型JPS+算法

JPS+算法的跳点识别规则选择的跳点没有考虑整体的障碍物分布情况，使得有些跳点的识别是冗余的，即跳点识别的有效性还可以进一步提高，据此提出了一种基于密度分类的角点判断规则，这样可以根据障碍物密度信息更有效地判断出主要跳点；同时也对于目标跳点的识别规则进行了修改，使得算法可以更好地收敛至终点。

2.1 主要跳点识别规则

2.1.1 基于密度的角点判断

对于一个栅格地图而言，最终实现的可行路径是由起点到终点，路径中的点是由一系列相邻点组成。给定栅格地图的情况下，从起点到终点的最短路径可以沿着障碍物的边界，但不能穿过障碍物的边界。在这种情况下，可以将相邻更近的障碍物视为一个组合，那么设计最短路径时，可以沿着障碍物边界外围的栅格。判断出障碍物组合的角点位置后，障碍物角点的斜对角方向就可以作为跳点，连接两跳点可以生成一条沿着障碍物外围的可行路径。一般的角点定义是位于障碍物组合外围的边界线的交点[15]，如图4中的边角加粗的栅格表示就是角点，其中加粗的直角对应的就是外围可行的跳点方向。

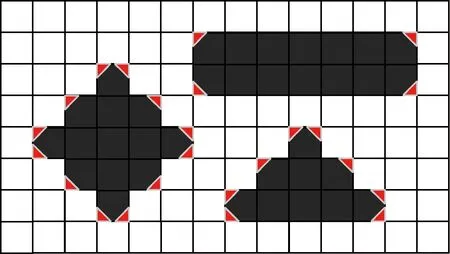
图4 一般角点判断规则Fig.4 Judgment rules of general corner

对于非角点的障碍物进行观察，可以看出非角点位置的障碍物，周围的障碍物数量明显大于位于角点位置的障碍物，数量的概念也可以理解为该点周围的障碍点密度更高。依据这个性质，我们定义了基于密度判定的“角点”。

DBSCAN密度聚类算法[16]是一种基于密度的空间聚类算法，该算法可以将满足给定密度的点划分成同一簇，从而完成不同障碍物组合的划分，形成任意形状的障碍物组合。

设给定的密度为MinPTs，给定的半径为Eps，数据点为xi，NEps(xi)表示的是与xi的距离不大于Eps的点的数量。在DBACAN算法中将数据点xi分为三类。

(1)核心点(core point)。若样本点xi距离为Eps的邻域中，包含了至少MinPTs个样本，即NEps(xi)≥MinPTs，则该样本点xi称之为核心点。

(2)边界点(border point)。若样本点xi距离为Eps的邻域中包含的样本数目小于MinPTs，但在其他的核心点的邻域内，则称样本点为边界点。

(3)噪声点(noise point)。既不是核心点也不是边界点的样本点。

将这个概念应用到判断障碍物组合角点中，可以将障碍物组合内部的点看作核心点，障碍物组合的角点视为边界点，而连续障碍物栅格数量小于给定的密度值的障碍物组合则就是噪声点。由此可见，在设定了合理的半径Eps和密度MinPTs的情况下，我们需要找的角点，其实就是边界点加上噪声点。边界点显而易见，噪声点同时可以视作只有角点组成的一系列相邻障碍物点。

图5 密度为6情况下障碍分布10种情况Fig.5 10 cases of obstacle distribution at density 6

2.1.2 主要跳点

角点斜对角的可行位置，，是栅格地图中与障碍物角点最近的可行点，可将这样的点表示为主要跳点，即图6中的圆圈所示的点。同时对比图4与图6，说明改进后可以减少主要跳点的识别数量。

图6中采用蓝色三角形标注但没有扩展跳点的栅格，对应的是基于密度判断规则下被忽略的一般角点，这说明引入基于密度的角点判断规则，可以在保证搜索效率的同时减少主要跳点的数量，使得规划算法的内存占用与运行速度都得到优化。

图6 基于密度的角点与主要跳点Fig.6 Corners and major jump points based on density

基于1.2节具体流程进行地图预处理，得到的与处理结果如图7所示。

与图3对比后可以看出，主要跳点数量有所减少，预处理后的直线跳点与对角跳点数量也都有效下降。这保证了在路径搜索的过程中，作为可扩展节点的数量有效降低，在保证能够搜索到最优路径的情况下，能够减少节点扩展，减少迭代过程。

由图7可以看出改进后的算法的预处理结果中，关键性的节点信息变少，在后续完成路径搜索过程中利用这些信息扩展的节点减少，搜索过程中对于无效节点的搜索时间得到节约，从而实现提高搜索效率的目的。

图7 改进算法地图预处理结果Fig.7 Improved algorithm map preprocessing results

2.2 目标跳点

在搜索过程中，由于目标点不属于关键的跳点，故需要建立到达目标点的跳转条件。当接近目标节点的时候，可以考虑在当前的节点与目标点之间建立一个中间跳点，这个点既满足当前点的跳跃条件，同时也满足目标点的跳跃条件，将该点称为目标跳点。JPS+算法中的目标跳点只会出现在对角线移动的时候，即移动方向是朝着目标点的，且在行距离或列距离中，到目标点的距离小于或等于当前节点到墙壁或跳点的对角线距离[14]。但JPS+中的目标跳点只能保证从当前点到目标跳点的路径是无碰撞的，目标跳点是否可以到达目标点需要进一步的验证。改进型JPS+算法修改了目标跳点的识别条件，使得目标跳点一定是可行点。

在不设置障碍物的条件下，从当前节点与目标点的可行八个方向分别延伸，得到的交集，就是满足跳跃条件的点，如图8中的TJP1、TJP2、TJP3和TJP4，其中TJP1、TJP4属于直线-直线前进，TJP2、TJP3属于直线-对角线前进。

显然TJP2、TJP3的路径更优，JPS+算法只考虑当前跳点对角线方向移动，且可以与目标点扩展方向延伸线相交的点，即图8中的TJP3(若Start在Goal对角线方向则TJP2与TJP3重合)，同时JPS+算法查找的目标跳点只能保证Start到TJP3无障碍，TJP3到Goal是否有障碍需重新验证。Iakushkin等[13]提出的改进算法在保证跳点可行的情况下考虑了图8中的4个目标跳点，且按照到目标点的距离进行排序，致使TJP1、TJP4在实际总规划距离次于TJP2的情况下，在搜索时顺序优于TJP2。而本文提出的改进型JPS+算法摒弃掉更为冗余的TJP1、TJP4，目标跳点的识别只有TJP2和TJP3(若Start与Goal共线或对角线方向则只有一个)，在向终点搜索的过程中，依旧保证路径最短，选择更优的直线-对角线的行进方向。

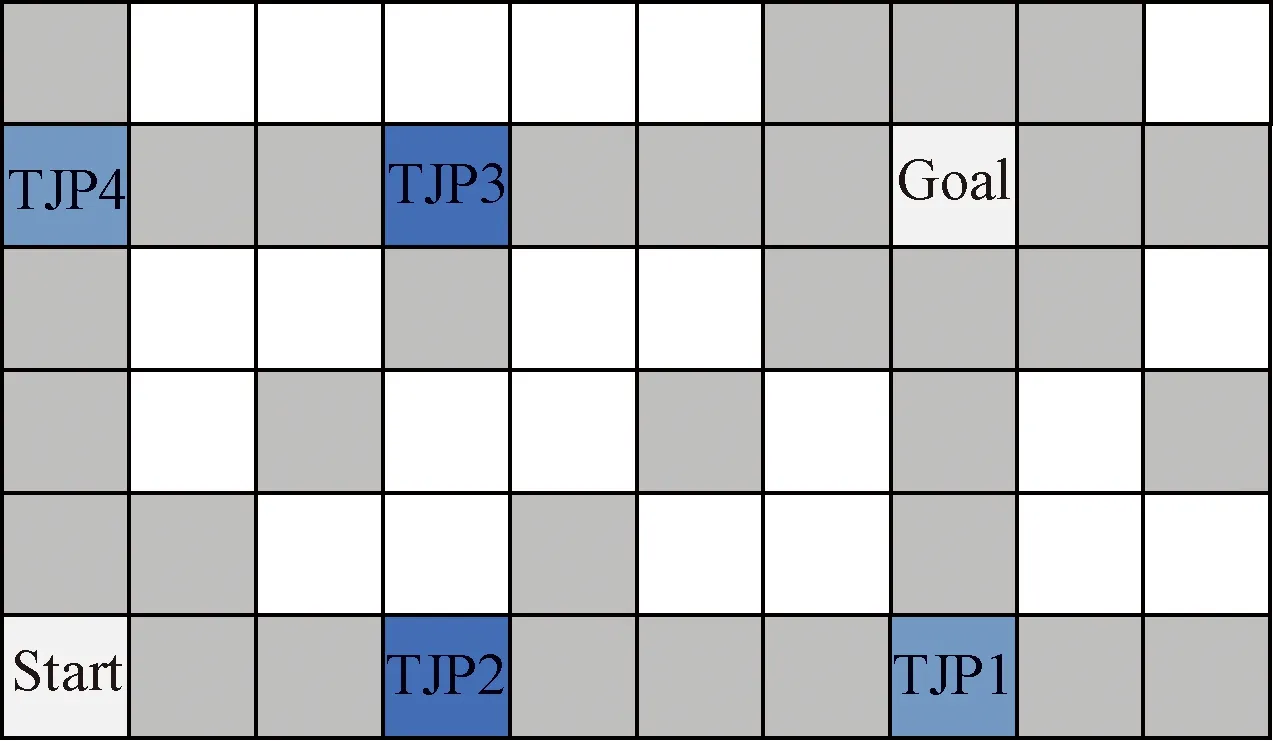
图8 目标跳点示意图Fig.8 Diagram of target jump point

2.3 路径搜索

路径搜索分为直线搜索和对角线搜索，在某一方向搜索时，有如下规则：①距离为正数n时，将在该方向与当前点距离为n的点存入openlist；②距离为0或为-n时，不做处理，停止搜索该方向。

不同于JPS+对于某个方向进行搜索时，在方向的距离为n时进行跳点的判断，改进后的算法在扩展之前进行目标跳点的判定工作，判定存在目标跳点则搜索成功，结束循环。改进后的JPS+算法在地图中的路径搜索结果如图9所示。

图9 改进型JPS+路径搜索结果Fig.9 Improved JPS+ path search results

3 仿真结果与分析

为验证改进算法的可行性和有效性，对A*算法、JPS+算法和改进型JPS+算法分别在给定复杂环境中进行10次仿真。实验环境为栅格地图，计算机配置为Window 10，内存大小为8.00 GB，使用仿真软件为MATLAB。模拟的栅格地图尺寸均为80×80，分为障碍率不同的随机地图和迷宫地图。由于JPS+算法与改进型JPS+算法的路径结果相同，故同一地图只展示一次，规划过程中的巡寻路时间、扩展点数和路径长度结果如表1所示。

表1 仿真结果对比Table 1 Comparison of simulation results

随机地图的规划结果如图10和图11所示。

图11 障碍物占比54.91%的随机地图Fig.11 Random map with obstacles accounting for 54.91%

在路径搜索过程中，改进型JPS+算法在地图的预处理过程采取了基于密度分类的方式检索了更为关键的跳点，这减少最终路径中的搜索节点数量，是加速搜索过程的一部分，但并没有改变对于搜索的路径的质量，故改进型JPS+算法最优路径结果和JPS+算法相同，也就是在路径的长度上是一致的。

随机地图的规划结果如图12和图13所示。

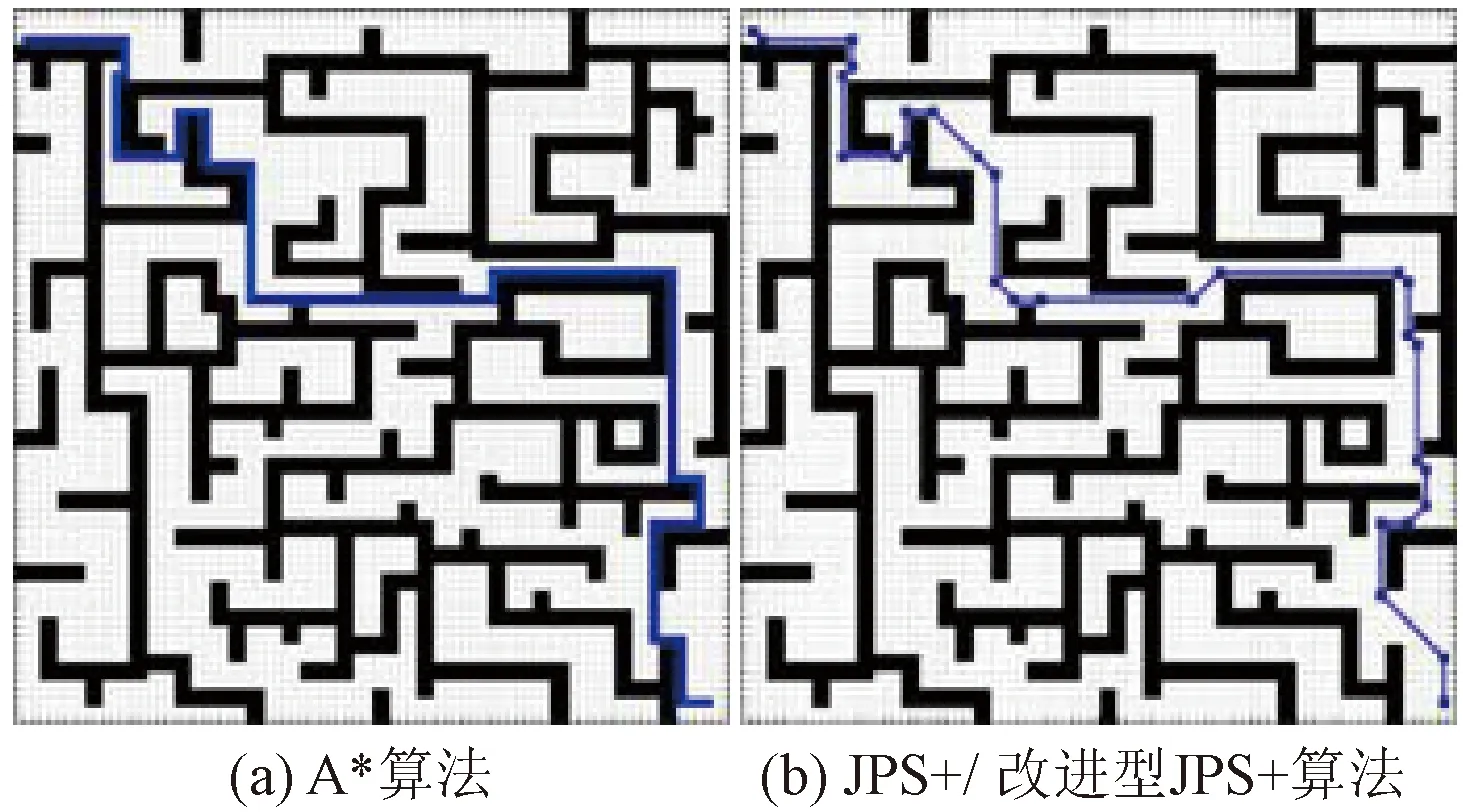
图12 障碍物占比32.03%的迷宫地图Fig.12 Maze map with obstacles accounting for 32.03%

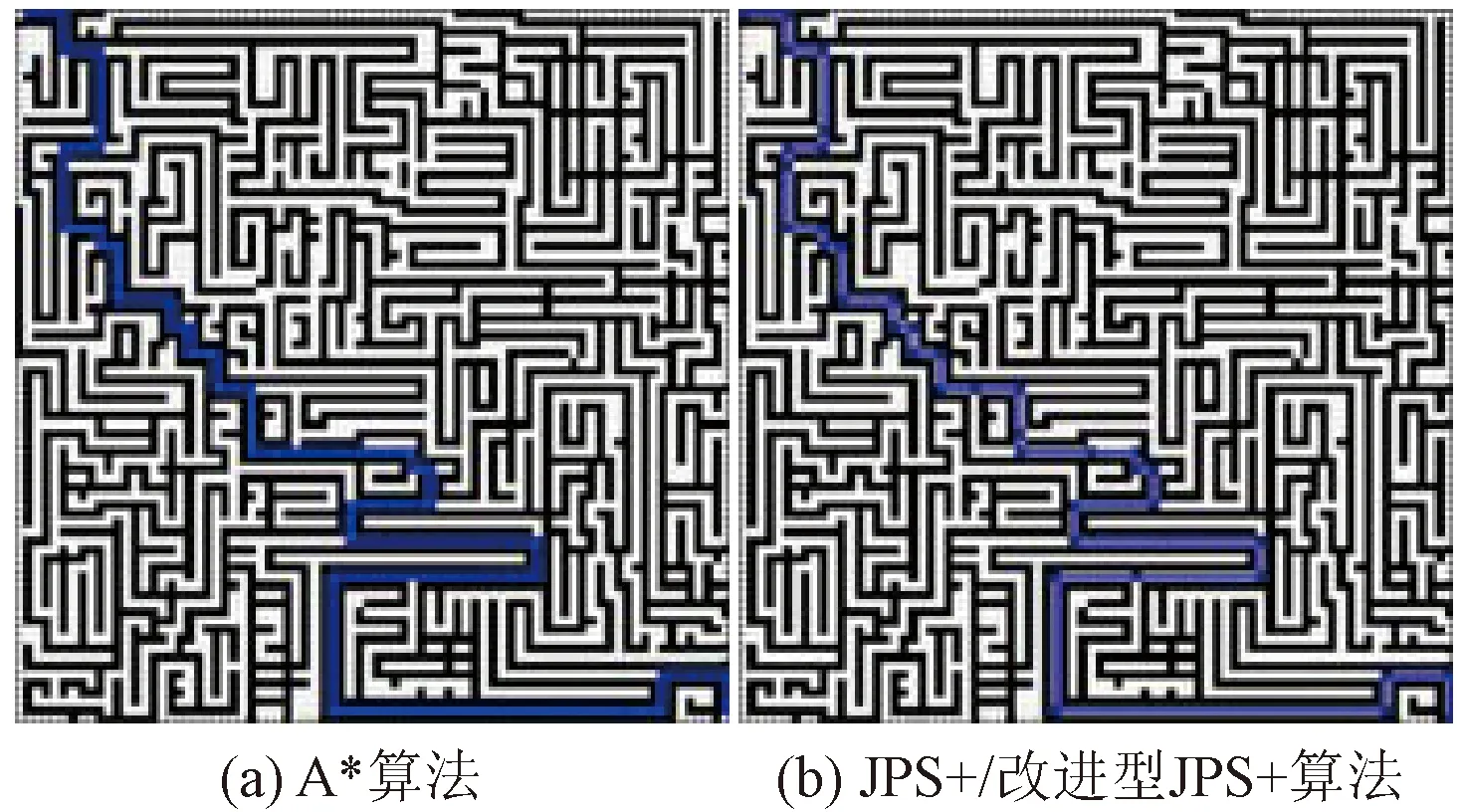
图13 障碍物占比49.00%的迷宫地图Fig.13 Maze map with obstacles accounting for 49.00%

相较于传统JPS+算法，改进型JPS+算法能够在规划出最短路径的同时，实现扩展节点的减少。

对于随机地图而言，障碍物占比越高，基于密度分类的跳点识别规则减少的冗余跳点就越多，在障碍率占比54.91%的随机地图中，扩展节点数量减少了43.31%，时间相较传统JPS+算法减少了4.00%。

由表1的数据可以看出，改进型JPS+算法与A*算法相比，不论是从规划时间、扩展节点数量和路径长度都可以展现出巨大的优势，上述四种地图均能够将时间规划缩短65%以上，扩展节点减少至少77.15%，路径长度也能有效降低。

对于迷宫地图而言，规则的地图确保了跳点一定位于转弯处，在此基础上改进型JPS+算法仍能保证规划时间有所优化，在障碍物占比为32.3%的地图相较传统JPS+算法缩短了8.23%，验证了改进策略对于规划效率提升的有效性。

综合来说，算法在不同的地图中都可以对路径规划的时间进行优化，而运行空间上的优化在障碍物分布不规律的地图中表现得更为明显。

4 结论

提出了一种基于密度分类实现预处理的改进型JPS+算法。新算法在进行地图预处理阶段，从障碍物密度出发，通过障碍物的密度信息找到不同障碍物组合的角点，进而完成主要跳点的搜索，同时对于目标跳点的搜索规则进行了更新，使得在预处理和路径搜索阶段的速度均得到提高，加快了搜索效率。在不同类型的地图中都进行了仿真实验，在障碍物分布不均匀的地图中可以有效提高运行效率、减少内存使用；在障碍物分布规律的地图中也能在障碍物占比小于一半的情况提升性能，能够满足正常的使用环境。结果表明，使用新的改进型JPS+算法进行移动机器人的全局路径搜索可以提高搜索效率，满足实际需求，具有一定的现实意义。