磁热耦合下不同注射方式对温度场的影响
2022-12-19王珂张璐安博孙光毅王永庆
王珂, 张璐, 安博, 孙光毅, 王永庆
(1.郑州大学力学与安全工程学院河南省过程传热与节能重点实验室, 郑州 450001;2.郑州大学机械与动力工程学院, 郑州 450001)
2022年全球癌症统计报告[1]中预计美国将出现191.8万例新癌症病例和60.9万例癌症死亡。2020年全球癌症统计报告[2]显示:世界癌症形势严峻,全球的癌症发病数和死亡数居高不下,癌症将是世界各国提高预期寿命的最主要的障碍。磁流体热疗已被证明是治疗癌症的一种有效方法,主要是由于其副作用低、效率高[3-4]。磁流体热疗[5]是指通过各种方式,将磁流体分布在治疗区域内,在磁场的作用下产热升温,达到治疗的目的。磁热疗的治疗效果很大程度上取决于治疗区域内的温度分布,需要将治疗区域温度控制在42 ℃以上,以便在不伤害健康组织的情况下消融恶性细胞[6-7]。
目前已有许多研究从不同的角度对磁流体热疗进行了研究,分析了磁颗粒的大小、外加磁场、生物组织参数等对磁流体热疗过程的影响。Xu等[8]建立了多场耦合模型,探究了肿瘤组织内磁场和温度的分布,确定了磁场强度对温度的影响。Shah等[9]研究了磁场参数、颗粒半径、浓度等重要参数对产热的影响。Tang等[10]通过使用Nelder-Mead算法,以产热功率来优化外加磁场参数。张宏波[11]建立了高斯分布的产热模型,研究了磁场不均匀性对温度分布的影响,并提出了非等剂量注射策略。Tang等[12]分析了单点和两点注射方式、磁流体剂量和浓度对温度场的影响。Dahaghin等[13]对单点注射和三点注射进行了比较,发现三点注射下的温度分布较为均匀。在以上研究中,大多采用恒定磁场强度进行产热功率的计算,注射方式选用中心点注射,同时未对治疗效果进行定量分析。仅有较少学者考虑了其他注射方式对温度分布以及治疗效果的影响。
在前人的研究基础上,通过COMSOL有限元软件,建立磁热耦合模型[14],探究亥姆霍兹线圈产生磁场的均匀性,以及通入电流大小对治疗区域的温度和治疗效果的影响。为了提升治疗效果,提出线性注射策略,比较在相同注射剂量下不同注射方式对温度分布的影响,同时以有效治疗体积这一参数量化了不同注射方式的治疗效果。
1 模型和方法
1.1 物理模型
本文中建立的物理模型如图1所示,考虑了半径为30 mm的健康组织和半径为10 mm的肿瘤组织,并且使用亥姆霍兹线圈作为磁场发生装置,在外部设置半径为250 mm空气域。
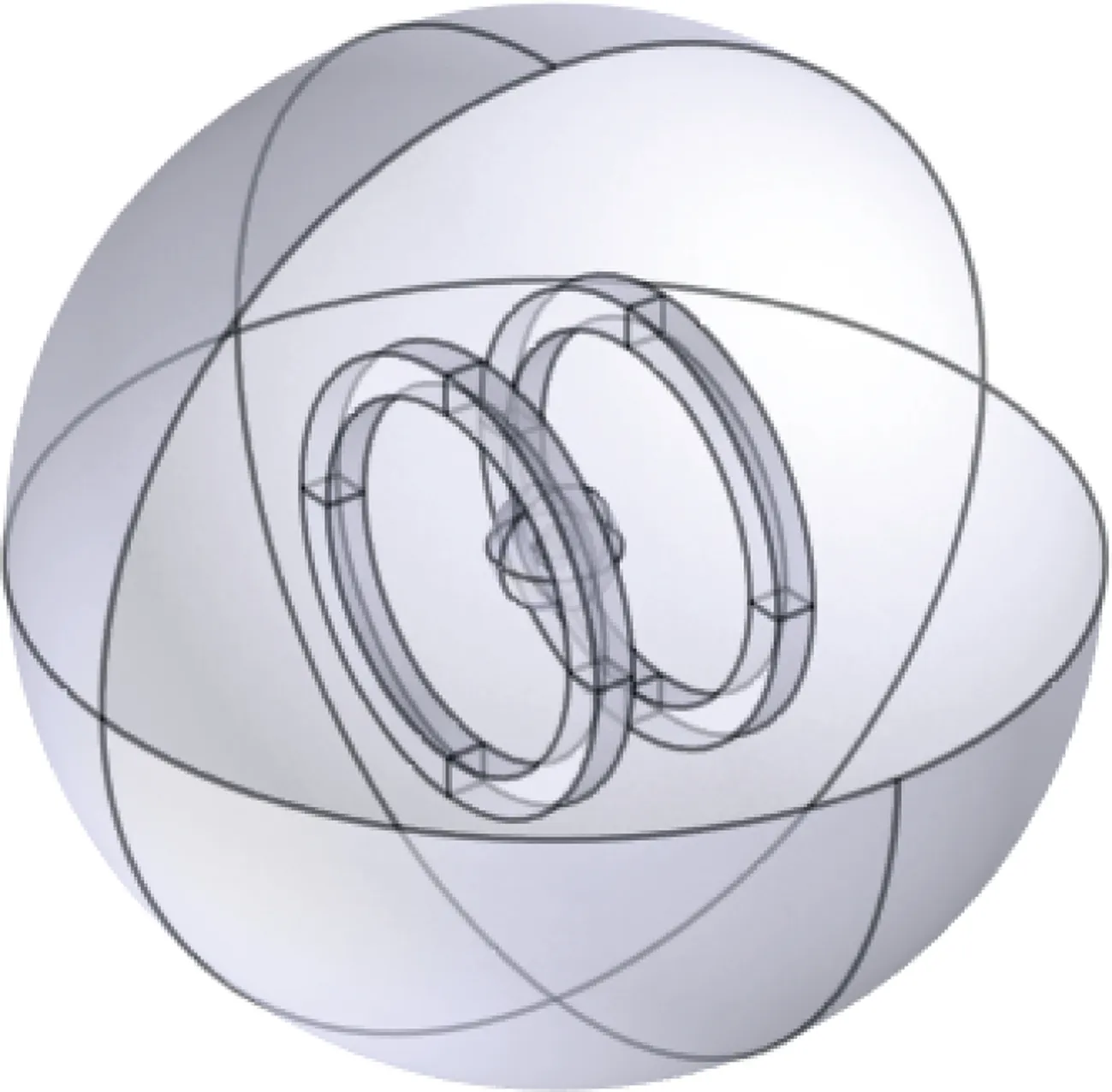
图1 物理模型Fig.1 Physical model
(1)线圈参数:半径100 mm,匝数30匝,宽度为20 mm,材料为铜,相对磁导率为1,电导率为5.998×107S/m。
(2)磁场求解的边界条件:空气域外部边界设置为磁绝缘边界条件,所有域中的磁场强度初始值为0。
(3)生物组织的边界条件:肿瘤组织边界采用Neumann边界条件,温度和热通量在交界处连续;健康组织外边界采用Dirichlet边界条件。
1.2 理论方法
1.2.1 磁场发生装置
亥姆霍兹线圈由一对彼此平行且共轴的载流线圈构成,电流的环绕方向一致。若两圆线圈的间距等于线圈半径时,则会在中央O点附近产生均匀磁场。线圈上任意点的磁感应强度B[15-16]为
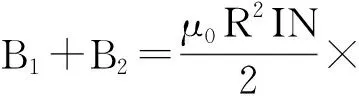
(1)
式(1)中:B1、B2分别为两圆线圈的磁感应强度,T;μ0为真空磁导率,H/m;N为线圈匝数;I为通入线圈的电流,A;R为线圈半径,m。
任意点的磁场B(x,y,z)与中心点处的磁场B(0,0,0)的相对偏差可以用不均匀度IH表示[16],其表达式为
(2)
1.2.2 生物传热
热疗期间,治疗区域的温度分布通过Pennes生物传热方程来预测[17],即

(3)
式(3)中:T为温度,℃;t为治疗时间,s;ρi、ci、ki分别为组织密度、比热容、导热系数(i= 1为正常组织,i= 2为肿瘤组织,i=b为血液);Qm为生物组织代谢热,W/m3;WMNP为磁流体的产热功率,W/m3;α为校正系数,一般取值为0.55。
磁流体在交变磁场中的产热功率[18]为
(4)
式(4)中:μ0为真空磁导率,μ0=4π×10-7T·m/A;χ0为平衡磁化率;H为磁场强度,A/m;f为磁场频率,Hz;τ为有效弛豫时间,s。
注入磁流体后的组织导热系数ki、密度ρi和比热容ci受磁流体体积分数φ影响,表达式为
(5)
ρi=φρMNP+(1-φ)ρ
(6)
ci=φcMNP+(1-φ)c
(7)
式中:kMNP、ρMNP、cMNP分别为磁颗粒的导热系数、密度、比热容。相关参数取值见表1。

表1 物性参数Table 1 Physical parameters
1.3 网格独立性验证
用5组数据来验证网格的独立性,如表2所示。相对误差均小于1%,综合考虑,最终确定网格数为163 544。

表2 网格独立性验证Table 2 Grid independence verification
1.4 模型验证
当磁场频率50 kHz,通入电流25 A时,经数值模拟计算,线圈产生的磁感应强度为6.096 mT。与理论计算结果6.131 mT相比,误差仅为0.56%,证明了模型磁场计算的正确性。
为验证温度场的准确性,与文献[19]中采用相同的条件,施加磁场频率为300 kHz,加热600 s后,组织中心处升温曲线如图2所示。从对比结果能够看出,本文的数值模拟结果与文献[19]基本吻合,验证了本文所建模型的可靠性。

图2 肿瘤组织中心点升温曲线Fig.2 Heating curve of center point of tumor tissue
2 结果与讨论
2.1 磁场分析
当线圈通入电流为25 A,频率为50 kHz的交流电时,分析亥姆霍兹线圈所产生的磁场强度。如图3所示为亥姆霍兹线圈产生的磁场分布图。从图3(a)中可以看出:在线圈附近产生较高的磁场强度,可达到13.8 kA/m;从图3(b)中可知,XOY平面上磁场强度由外向内逐渐增加,在中心区域能够产生较高的磁场强度,中心磁场强度可达4 881.4 A/m。磁场强度与频率的乘积小于5×109,符合Hergt安全标准[20]。
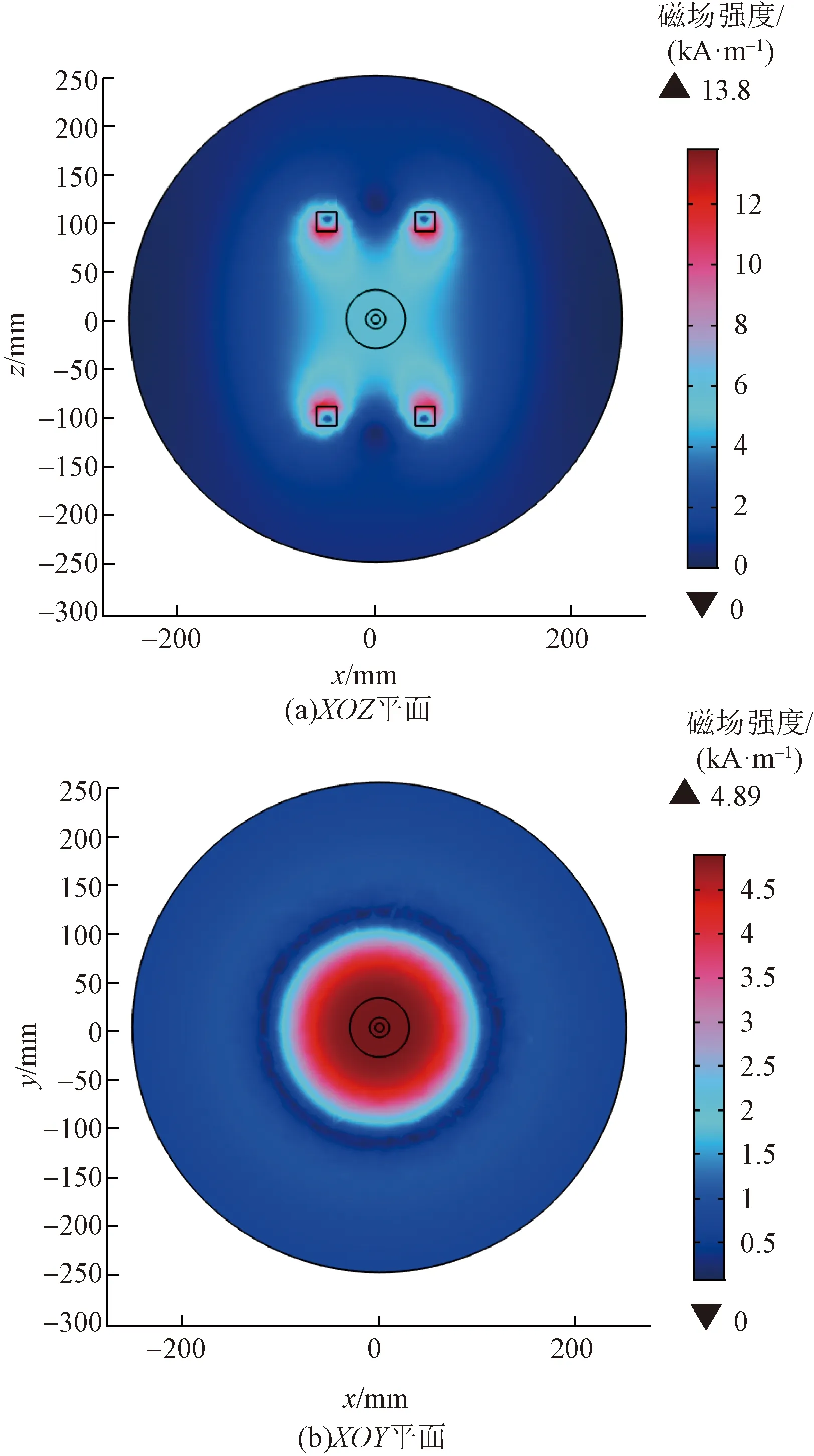
图3 不同平面上的磁场分布图Fig.3 Magnetic field distribution diagrams on different planes
如图4所示为x轴线(y=0)的磁场不均匀度差异图。线圈产生的磁场在中心处均匀性很强,不均匀度仅在1%以内。因此,越靠近两线圈中心点处,磁场均匀性越高,距离中心点处越远,磁场越不均匀。
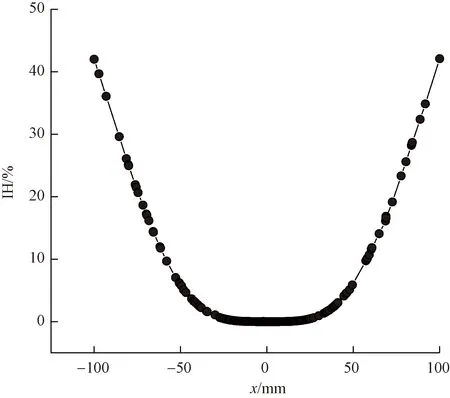
图4 中心轴线上的磁场不均匀度Fig.4 Magnetic field non-uniformity on the central axis
2.2 温度场分析
在磁流体颗粒半径为10 nm,体积分数为1.5%时,将磁场与温度场耦合,得到如图5所示的XOZ截面组织温度场分布图。从图5中可以看出,高温区域主要集中在磁流体注射区域,最高温度为54.7 ℃,肿瘤组织与健康组织交界处温度为40.8 ℃,正常组织的边缘温度保持在左右37 ℃,不会对正常组织造成损伤。

图5 XOZ平面温度场的分布图Fig.5 Distribution diagram of XOZ plane temperature field
2.3 电流大小对磁场以及温度场的影响
通过调节电流大小来改变磁场,探究线圈通入的电流对治疗区域的磁场以及温度分布的影响。通入不同电流大小下X轴线上磁场强度分布图如图6所示。当线圈通入的电流I为20~25 A时,中心点处的磁场强度分别为3 905.1、4 100.4、4 295.6、4 490.9、4 686.1、4 881.4 A/m。通入电流每增加1 A,磁场强度约增加195.3 A/m。
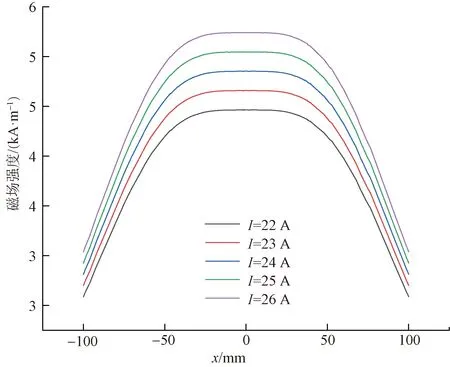
图6 不同电流大小下x轴线上磁场强度分布图Fig.6 Distribution of magnetic field intensity on the x-axis under different currents
有效治疗体积为肿瘤组织内温度大于42 ℃的区域。将有效治疗体积与肿瘤组织的体积之比称为有效治疗体积百分数。图7所示为通入不同大小电流时,组织中心处的温度和有效治疗体积。通入电流为20~25 A时,中心温度分别为48.4、49.6、50.8、52.1、53.4、54.8 ℃,有效治疗体积分别为710.8、898.8、1029.6、1242.3、1471.0、1747.6 mm3,有效治疗体积百分数分别为17.1%、21.5%、24.7%、29.8%、35.3%、41.9%。随着磁场强度的增加,治疗区域的温度和有效治疗体积逐渐增加。
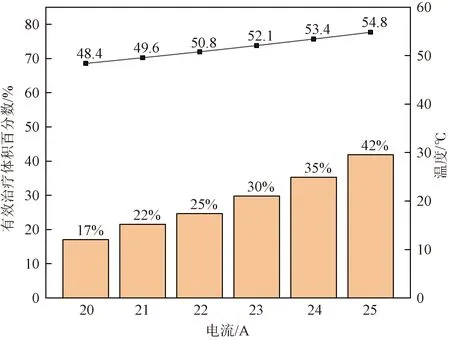
图7 不同电流大小下中心温度和有效治疗体积Fig.7 Core temperature and effective treatment volume under different currents
2.4 不同注射方式对温度分布以及治疗效果的影响
治疗区域内的温度分布在热疗中十分重要。采用单点注射,热量会在注射点周围聚集,使得中心处温度过高,影响温度分布的均匀性。因此本文在注射剂量相等的条件下,比较了不同注射方式对温度场的影响。考虑了沿肿瘤中心线性均匀注射,在肿瘤组织内中心注射量大、在两边注射量少的线性不均匀注射,多点注射这三种注射方式,并将其与中心点注射进行对比。图8所示为在施加30 min外加磁场强度4 kA/m、磁场频率50 kHz的条件下,这4种注射方式的温度场分布。
从图8中能看出,采取中心点注射时组织温度最高,为49.8 ℃,其他3种注射方式下的温度最高为46.8、48.1、45.3 ℃。由此可见,采取中心点注射时,组织中心可以达到较高的温度,但区域内温度差大,温度分布不均匀;而多点注射时,组织内温度分布则较为均匀。
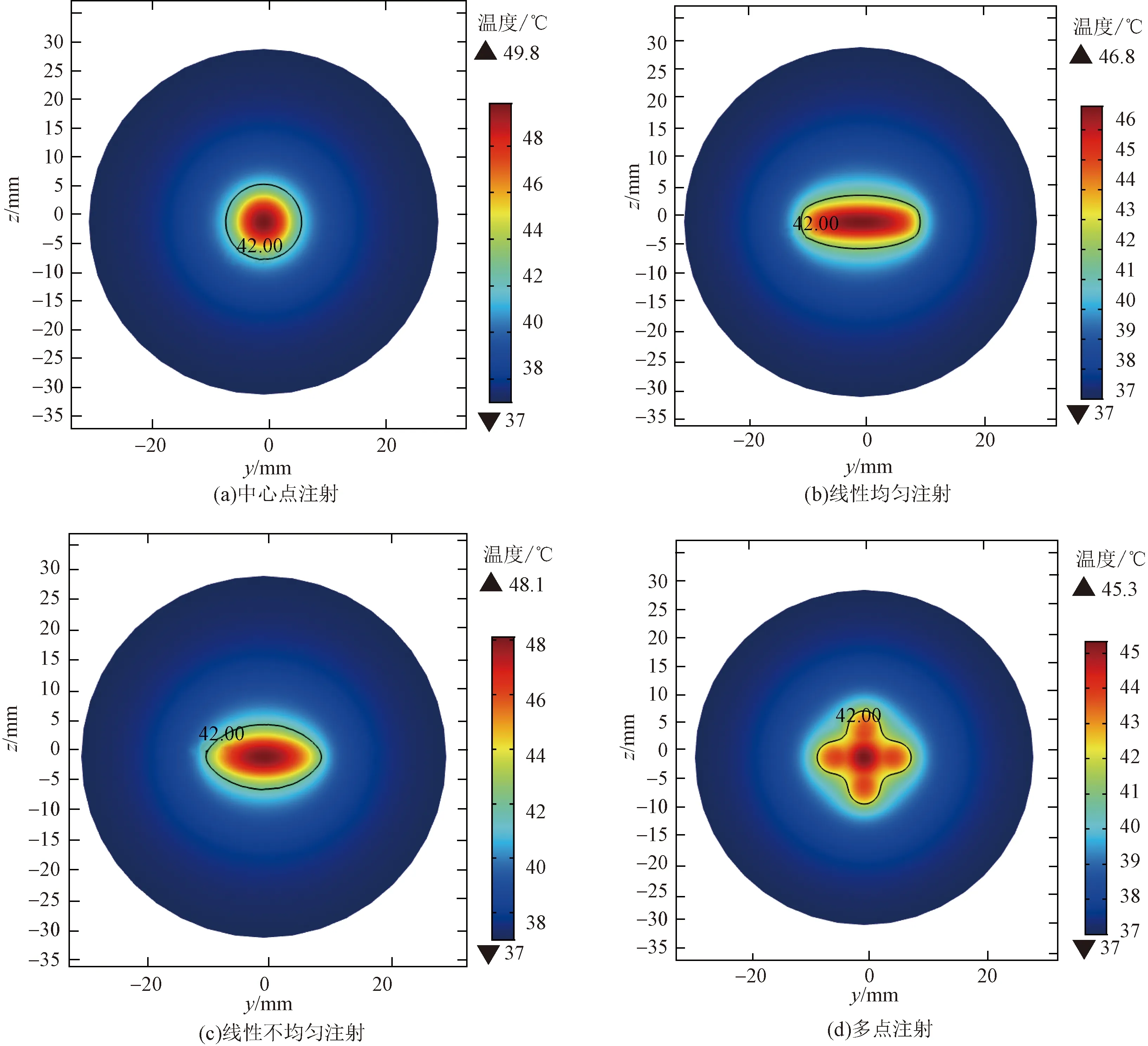
图8 不同注射方式下温度分布界面图(YOZ平面)Fig.8 Interface diagram of temperature distribution under different injection methods(YOZ plane)
图9所示为不同注射方式下的有效治疗体积百分数和最高温度。这4种注射方式下的有效治疗体积分别为1 156.4、961.7、1 067.9、704.0 mm3,有效治疗体积百分数分别为28.5%、23.7%、26.3%、17.4%。从图9中得出,在相同的磁场条件下,采用中心点注射时有效治疗体积最大,治疗效果最好。
但是,在相同的外加磁场条件下,不同的注射方式会导致治疗区域所能达到的最高温度不同,无法准确比较治疗效果。因此,对外加磁场进行调节,使不同注射方式下的最高温度均保持在48.0 ℃附近,进而对治疗效果进行对比。对比结果如图10所示,此时,中心点注射、线性均匀注射、线性非均匀注射和多点注射所需外加磁场频率分别为45、54、50、62 kHz,有效治疗体积分别为806.6、1 258.5、1067.9、1 530.7 mm3,有效治疗体积百分数以分别为19.9%、31.0%、26.3%、37.7%。由此可得出,48 ℃为约束的条件下,采取多点注射时有效治疗体积最大,治疗效果最好,线性均匀注射次之,而中心点注射,治疗效果最差。
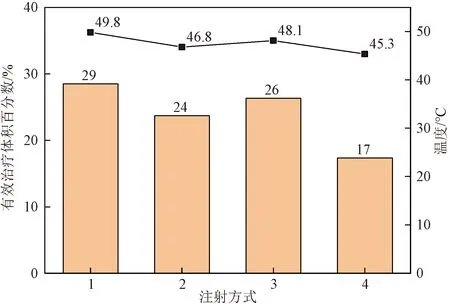
图9 相同磁场下不同注射方式的有效治疗体积百分数Fig.9 Effective treatment volume percentage of different injection methods under the same magnetic field
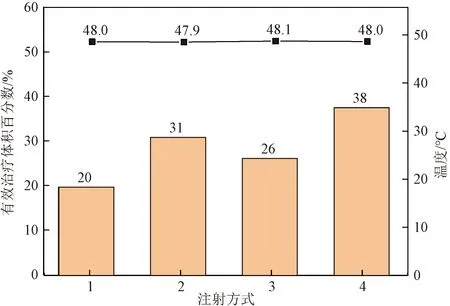
图10 相同温度下不同注射方式的有效治疗体积百分数Fig.10 Effective treatment volume percentage of different injection methods at the same temperature
3 结 论
本文采用有限元方法,建立了磁热耦合模型,探究了亥姆霍兹线圈的产生磁场的均匀性,考虑了通入电流大小对磁场以及温度场的影响,量化了不同注射方式下的治疗效果,并得出以下结论。
(1)线圈能够在治疗区域产生均匀的磁场,磁场的不均匀度仅有1%。当通入25 A的电流时,中心磁场强度可达到4 881.4 A/m;与温度场耦合后,组织最高温度为54.8 ℃,肿瘤组织与健康组织交界处温度为40.8 ℃,治疗体积为3 148.8 mm3。
(2)通入线圈的电流每增加1 A,线圈所产生的磁场强度增加195.3 A/m,随着磁场强度的增加,组织的温度和有效治疗体积也逐渐增加。
(3)当外加磁场条件相同时,采用中心点注射时,组织内的温度最高为49.8 ℃,有效治疗体积为1 156.4 mm3,治疗效果最好;保持治疗区域最高温度为48 ℃,采用多点注射治疗效果最好,有效治疗体积为1 530.7 mm3。
因此,采用多点注射技术,可以使治疗区域的温度分布较为均匀,有效治疗体积较大,达到更好的治疗效果。
