泥泵轴端螺纹应力集中系数及其影响因素
2022-12-19祝志远曹蕾武永顶
祝志远, 曹蕾, 武永顶
(中交疏浚技术装备国家工程研究中心有限公司, 上海 200082)
泥泵是挖泥船输送疏浚介质的核心装备,而泵轴是泥泵传递动力的关键部件,泵轴的可靠性直接关系到疏浚系统能否正常推进施工进程。近年来,中外大型挖泥船频发泥泵断轴事件,每次断轴必将导致挖泥船停工3~4 d,严重影响生产进度与效益,因此该问题已在行业内引起广泛关注。目前,工程设计中通常根据机械设计手册中提供的校核流程来校核泵轴的屈服强度。在屈服强度满足规范要求时,通常认为泵轴的疲劳强度也满足要求,因此不再进行专项校核。然而,对于运行工况复杂多变的泥泵,其泵轴所承受的交变载荷特性不同于普通的水泵泵轴,容易产生疲劳破坏,需要提高其疲劳强度校核精度。
疲劳破坏是结构损伤累积的结果,即使结构受到的最大应力小于材料的屈服强度,在一定幅值的交变载荷作用下,经过一段时间的作用后,也可能发生破坏[1]。疲劳破坏易发生于结构物上应力集中较为严重的区域,如孔洞、台肩等结构的不连续处。许多研究表明,具有螺纹的结构由于螺纹处的截面发生突变,有的甚至形成缺口效应,在螺纹根部有较大的应力集中效应,该部位在循环交变载荷的作用下容易产生疲劳破坏[2-3]。段焱森等[4]研究了某风力机叶片高强连接螺栓的疲劳断裂特征,进行了该螺栓材料的高频疲劳试验,并根据试验结果拟合出了螺栓材料的S-N(应力-寿命)曲线方程。
对于工程上的结构,一般采用名义应力法计算构件的高周疲劳寿命,该方法是基于线性累积损伤理论和S-N曲线的评估方法,计算过程中,需考虑应力集中系数等影响因素对材料S-N曲线进行修正,得到实际构件的S-N曲线,以求得准确的疲劳寿命[5]。应力集中系数手册[6]中提供了各种尺寸、形式的台肩、键槽等结构的应力集中系数,而对于螺纹的应力集中系数则未结合螺纹的具体形式给出相应的推荐值。
雷宏刚等[7]建立了8种规格的螺栓单螺纹有限元模型,计算了拉伸载荷作用下螺纹根部的理论应力集中系数,结论指出应力集中效应对螺栓的静强度影响较小,但对其疲劳强度影响较大。杜运兴等[8]忽略了螺纹升角的影响,建立了螺栓与螺栓球啮合的第一圈螺纹的轴对称有限元模型,计算得出了多种型号螺栓的应力集中系数。杨光等[9]忽略螺纹升角,取螺栓上第一圈螺纹进行了研究,求出了摩擦型高强度螺栓应力集中系数的解析解。焦晋峰等[10]对某螺栓进行了常幅疲劳试验,拟合得到该螺栓的S-N曲线,并通过数值模拟求得螺栓承压面下第一个螺纹根部的理论应力集中系数。包括上述研究在内的多数研究成果均针对标准的普通螺栓螺纹,普通螺纹相对于螺栓杆向下凹陷形成缺口效应,有较大的应力集中系数。而泥泵泵轴端部为凸起的梯形螺纹,针对梯形螺纹这种传动螺纹的应力集中系数的研究较少。两种螺纹结构形式和螺纹牙尺寸不同,不能直接将普通螺纹的应力集中系数等效应用于梯形螺纹。因此,有必要对泥泵轴端螺纹的应力集中系数进行深入研究。
以3 500 m3/h绞吸挖泥船舱内泵的模型泵为研究对象,研究泥泵泵轴上梯形螺纹根部的应力集中情况,在ANSYS 中建立泵轴梯形螺纹的参数化简化模型,计算在轴向拉伸载荷作用下螺纹根部的应力集中系数,并分析螺纹根部倒角尺寸、螺纹牙高、螺距、螺纹位置等因素对应力集中系数的影响。本文计算所得应力集中系数可用于修正材料的S-N曲线,从而提高泵轴疲劳寿命预报的精确度,各因素的影响规律可为泵轴结构优化设计提供参考。
1 几何模型
1.1 泵轴几何模型
3 500 m3/h绞吸挖泥船舱内泵的模型泵泵轴整体示意图如图1所示。泵轴右端最外侧为梯形螺纹,用以和叶轮进行联接。螺纹左侧轴径渐变,与轴肩以圆弧连接,保证平滑过渡。
轴肩和右侧第一个梯形螺纹之间的区域应力集中情况较为严重,在工作交变应力的作用下,容易发生疲劳破坏,是需要重点关注的区域。泵轴右侧局部结构放大图及相关尺寸如图1所示,可知,左侧轴径D= 187 mm,右侧最小轴径d= 160 mm,轴肩过渡圆弧半径为R=24 mm,右端轴上车有梯形螺纹,圆弧与小轴的切点到第一个螺纹根部的距离L=12.4 mm。

图1 泵轴几何模型Fig.1 Geometrical model of pump shaft
1.2 梯形螺纹几何模型
梯形螺纹代号为Tr180×72P18,其中,Tr表示梯形螺纹,180表示螺纹公称直径,螺纹牙高为H=10 mm,72表示螺纹导程,轴端螺纹为四头螺纹,螺距P= 18 mm。螺纹牙的具体尺寸按照GB/T 5796.1—2005设计,如图2所示。螺纹牙型角为30°,螺纹根部倒角半径为r= 1 mm。
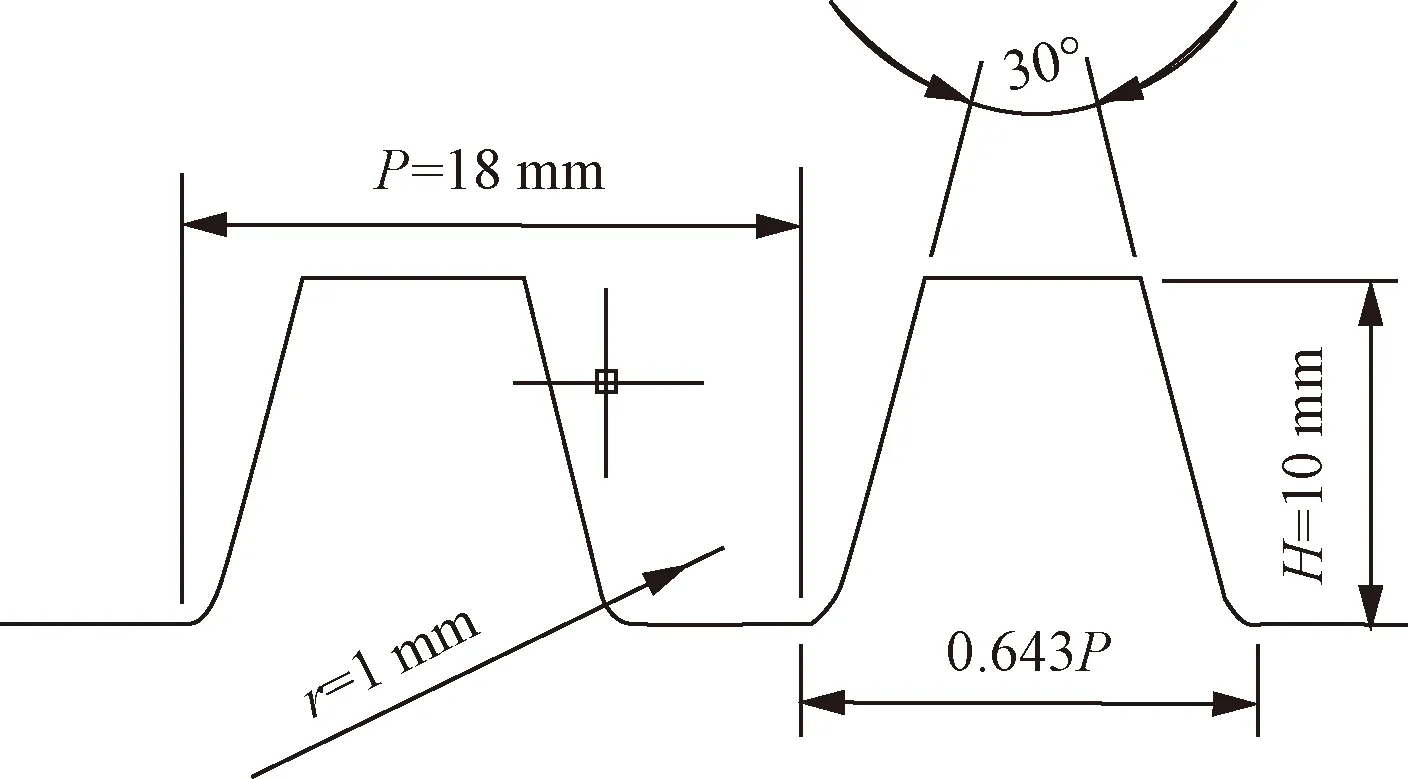
图2 梯形螺纹牙型参数示意图Fig.2 Schematic drawing of the trapezoidal thread
2 应力集中系数Kt
2.1 Kt的基本概念
在等截面的构件中,应力分布均匀,当构件上有沟槽、孔、缺口、台阶等形状急剧变化的结构时,这些地方由于截面尺寸突变,应力不再是均匀分布,在四周小范围内,将产生局部的高应力区,应力最大值远大于由基本公式计算得到的应力值,这种由于构件的截面尺寸突变而引起应力局部增大现象称为应力集中[6]。应力集中系数Kt用来表示应力集中的程度,其大小,只与结构的外形和尺寸有关,与材料的属性无关。应力集中处的局部应力值,有时可能很大,能使物体产生疲劳裂纹,也可能使脆性材料结构发生静力破坏,是结构损坏的重要原因之一。
2.2 泵轴螺纹Kt的定义
应力集中处的最大值σmax与适当选取的基准应力σn的比值,定义为应力集中系数Kt,表达式为
(1)
基准应力可以人为规定,取值的方式并不唯一,一般选择变截面结构最小截面段上远离应力集中区域的截面平均应力[11]。对于图1所示泵轴结构,选取右端小轴上的距离螺纹较远处的平均应力为基准应力。
实际工程中,局部应力可以采用光弹性法等试验方式测得。有限元技术的发展,使得科研工作者可以以较小的成本准确求得复杂结构的局部应力。本文采用有限元建模求出轴肩-螺纹局部区域的最大应力σmax,从而求出应力集中系数Kt。
3 有限元计算
3.1 有限元模型
通过有限元方法计算研究该模型泵轴端螺纹在轴向拉伸载荷作用下螺纹根部的应力集中系数。在ANSYS中进行参数化编程建立有限元模型,采用数值模拟的方法求解应力集中系数。参数化建模可以方便修改模型尺寸等参数,以讨论模型尺寸等因素对计算结果的影响。考虑以下三个因素对模型进行简化。
(1)当螺纹升角较小时,应力沿螺纹的分布情况与没有螺纹升角时基本相同[12]。因此建立螺纹模型时不考虑螺纹升角。
(2)轴向拉伸载荷作用下,各个螺纹牙的受力不均衡,一般螺纹啮合的第一圈螺纹的牙根处应力值最大,该处也最容易发生疲劳破坏[13]。因此取第一圈螺纹,建立泵轴单螺纹模型。
(3)忽略螺纹升角后,模型泵局部结构为轴对称结构且轴向拉伸载荷也为轴对称载荷,因此将三维实体模型简化为二维轴对称模型,可以减小模型中单元数量从而减小计算量。
论坛期间,内蒙古自治区水利厅农牧处处长王向东针对“内蒙古的节水灌溉发展前景和展望”进行了全面介绍,他介绍说内蒙古农牧业节水灌溉形势非常严峻,干旱缺水问题十分严重,威胁到农业乃至整个内蒙古经济发展。当前内蒙古农牧业灌溉发展面临的一些突出的问题亟待解决:一是农牧业用水比例大,用水效率低;二是用水结构不合理,水资源分布与利用地区不均衡;三是灌溉工程老化失修,节水灌溉发展滞后;四是灌溉发展缺乏刚性约束,资源浪费问题突出。
根据泵轴轴肩-螺纹局部几何尺寸和梯形螺纹牙型尺寸,在ANSYS 中建立泵轴螺纹结构的简化轴对称有限元模型,模型采用PLANE82轴对称单元,为8节点16自由度单元。对于四边形和三角形的混合网格,该单元计算精度较高,可以适应不规则形状而计算精度损失较少。对于PLANE82单元,建立轴对称模型时需保证Y轴为对称轴,且轴对称截面在XOY平面内;模型单元面积为正,即在X>0区域建模,如图3所示。

图3 轴对称有限元模型Fig.3 Axisymmetric finite element model
模型泵的材料采用高强钢42CrMo,对单元赋予材料属性:弹性模量E= 2.06×105MPa,泊松比为0.3。对轴肩-螺纹局部结构网格进行细化,单元大小为0.1 mm,采用三角形网格进行自由划分;两侧轴的单元尺寸为4 mm,采用四边形单元进行自由划分,共生成32 435个单元,节点数68 988。重点关注中间轴肩-螺纹局部结构的应力状态,两侧轴计算域取适当长度以减小对中间区域的干扰。如图3所示,在泵轴左侧端面施加固定约束,右侧端面施加压强为p= 10 MPa的轴向拉伸载荷,则计算应力集中系数时的基准应力σn=10 MPa。
3.2 计算结果
在ANSYS中进行求解,后处理得到结构的变形示意图和轴向(Y方向)应力云图,分别如图4、图5所示。图4重叠显示了泵轴变形前后的形状,黑色的几何模型边界为泵轴变形前的形状,蓝色的网格模型为变形后的形状,可以看出结构有Y方向的应变。在对称轴边界上,即Y轴上的节点,没有径向的位移,说明 加正确。

图4 结构变形图Fig.4 Structural deformation diagram

图5 轴向应力云图Fig.5 Axial stress contour
由图5可以看出在轴肩-螺纹区域,应力较大,最大应力点出现在螺纹根部,为23.992 5 MPa,即σmax=23.992 5 MPa,由式(1)可以求得应力集中系数Kt= 23.992 5/10 = 23.992 5。
图6(a)为轴肩圆弧处的局部应力云图,轴肩处最大应力出现在过渡圆弧与小轴径的切点附近,值为16.354 5 MPa,由式(1)求得此处应力集中系数为1.635 45,小于螺纹根部的应力集中系数,所以螺纹根部处更易发生破坏。图6(b)为截取的小轴上远离螺纹的局部应力,由于单元形状不规则,截取部分形状不规整,但并不影响云图的查看。由图6(b)可以看出,最大应力为10.02 MPa,最小应力为9.98 MPa,与10 MPa的基准应力基本相等,验证了有限元模型的正确性。
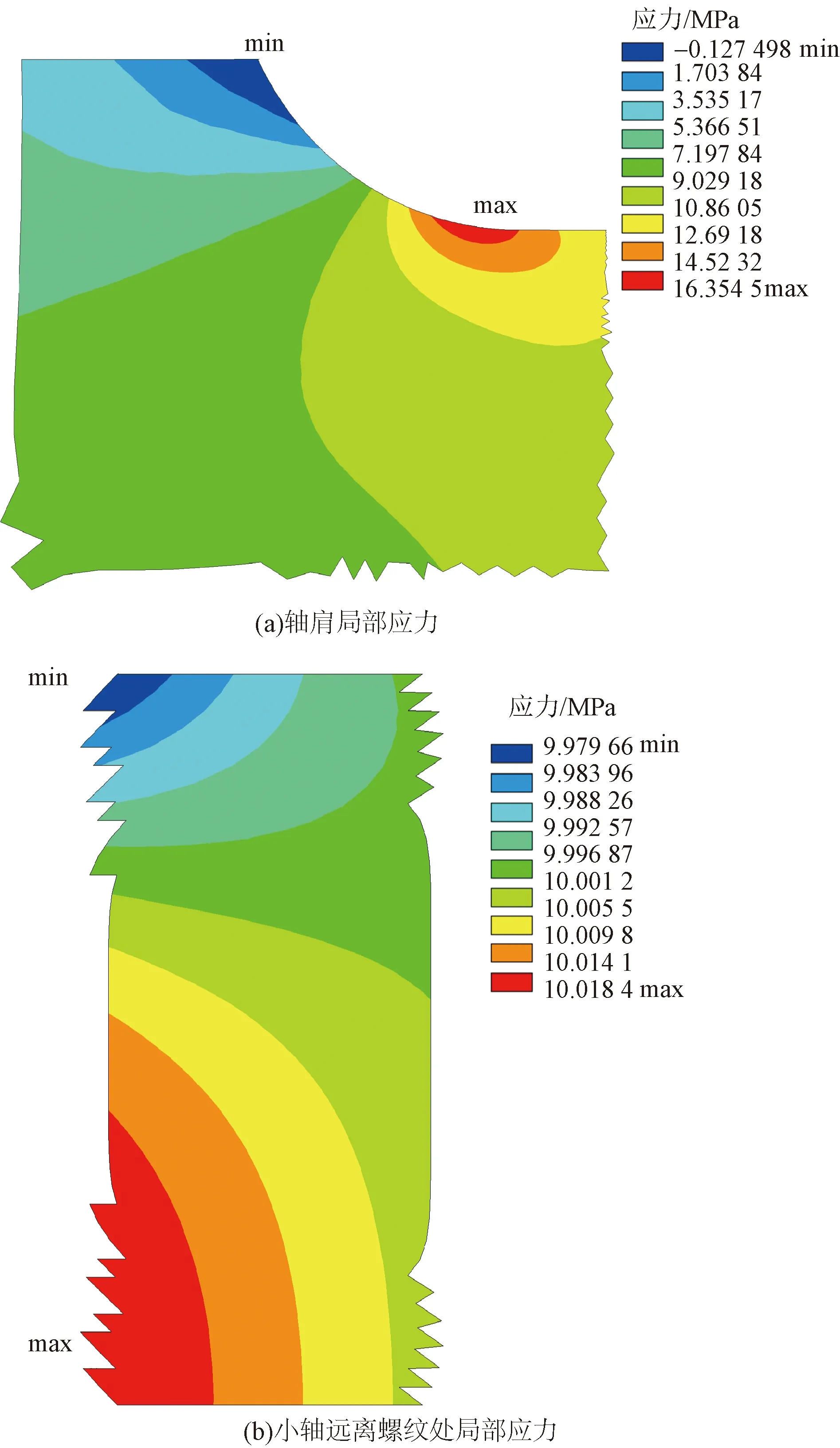
图6 轴向局部应力云图Fig.6 Local axial stress contour
3.3 网格无关性分析
为了保证有限元计算结果的准确性和高效性,改变轴肩圆弧和螺纹附近的单元尺寸,计算得到如图7所示结果。横轴为轴肩和螺纹局部区域的单元尺寸,纵轴为基于局部最大应力计算得到的应力集中系数Kt。随着单元尺寸的减小,网格精度提高,Kt逐渐增大且趋于稳定。单元尺寸为0.1 mm时,继续加密网格,Kt变化不大,说明有限元计算结果已逐渐收敛,此时得到的结果已经非常精确。网格越密,计算效率越低,综合考虑有限元的计算精度和计算效率,本研究中选择0.1 mm的单元尺寸较为合适。3.2节中轴肩和螺纹区域的单元尺寸为0.1 mm,因此可以认为计算得到的局部最大应力和应力集中系数结果可靠。下文各影响因素的计算过程中,单元尺寸都取0.1 mm。

图7 单元尺寸对应力集中系数的影响Fig.7 Influence of element size on stress concentration factor
4 影响因素分析
实际结构中泵轴的轴径大小由多种因素决定,一般难以改变,然而螺纹的布置和螺纹牙的尺寸参数相对容易修改,且对泵轴应力集中系数有较大影响。本节分别改变螺纹根部倒圆角半径、螺纹牙高度、螺距和轴肩与第一圈螺纹之间距离的大小,研究螺纹根部应力集中系数的变化情况。
4.1 螺纹根部倒角半径
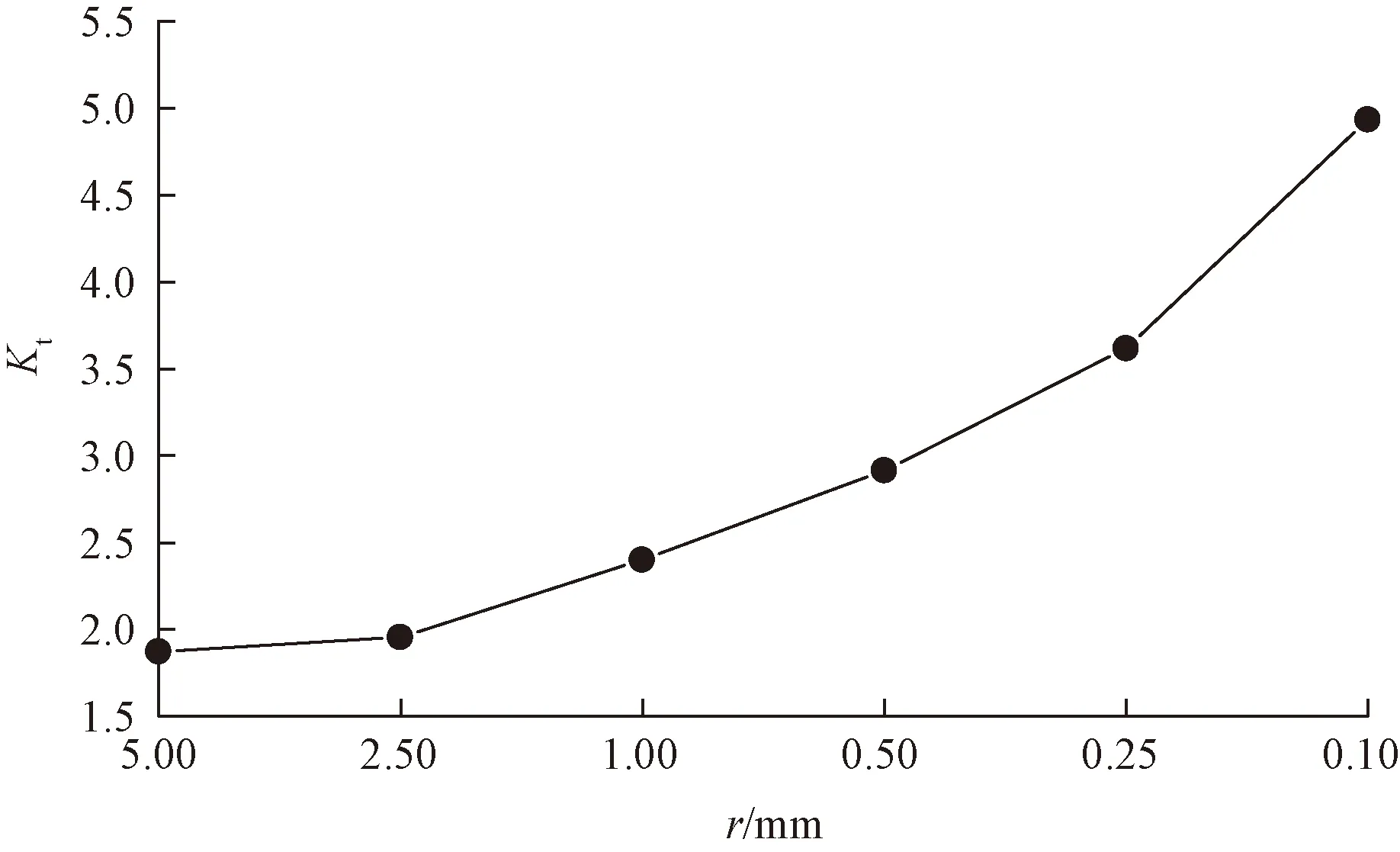
图8 应力集中系数随倒角半径变化曲线Fig.8 Stress concentration factor-fillet radius curve
4.2 螺纹牙高
其他螺纹参数不变,改变螺纹牙的高度H,计算得到表1所示结果。可以看出,随着牙高H的增大,最大应力和应力集中系数增大。但是增大的幅度较小,H从6 mm增大到16 mm,Kt值仅增加了0.019 27,说明螺纹牙高度对应力集中系数的影响不大。

表1 螺纹牙高的影响Table 1 The effect of thread height
4.3 螺距
仅改变螺距P,其他螺纹参数不变,计算结果如图9所示。随着螺距P的增加,Kt逐渐增加,拟合相关数据得到Kt和P的关系式为:Kt= 0.034P+ 1.781 2;线性相关系数R的平方为0.997 7,说明两者有良好的线性相关关系。具体设计时螺距可根据相关规范和此结论在一定范围内选择,或对选定的螺距进行微调。
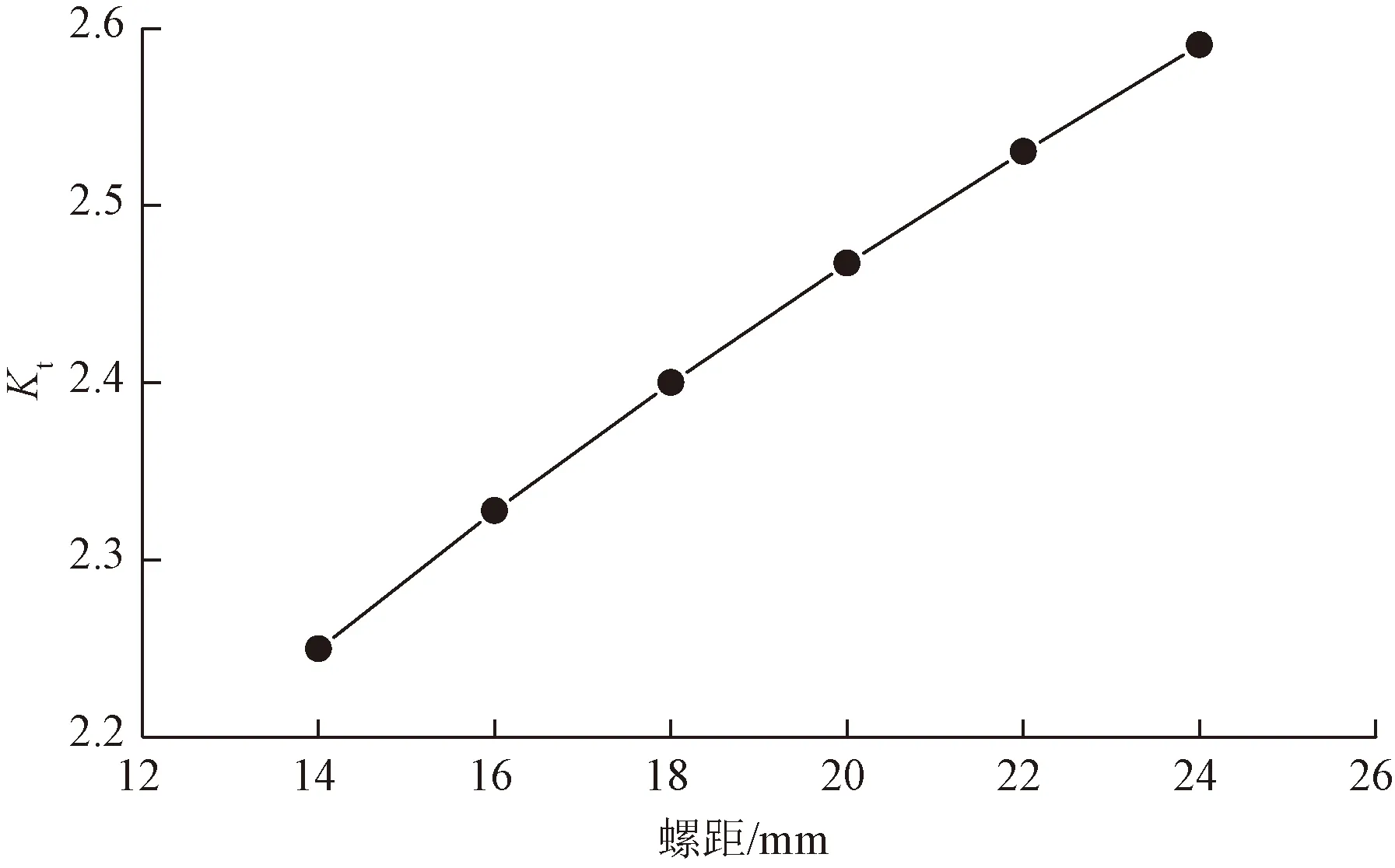
图9 应力集中系数随螺距变化曲线Fig.9 Stress concentration factor-pitch curve
4.4 螺纹位置
螺纹尺寸参数保持不变,改变轴肩圆弧与小轴切点和螺纹根部之间的距离L,计算得到图10所示变化趋势。随着L的增大,螺纹距离轴肩越远,螺纹高应力区和轴肩高应力区的相互影响逐渐减弱,应力集中系数逐渐减小,到达一定距离后减小的趋势减缓。
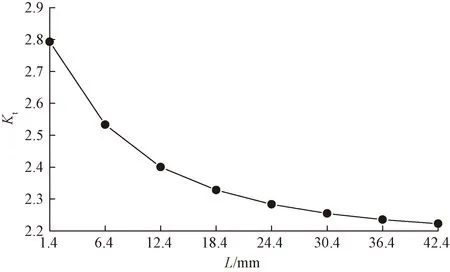
图10 应力集中系数随螺纹位置变化曲线Fig.10 Stress concentration factor-thread position curve
图11所示为L=1.4 mm时,轴肩和螺纹区域的应力云图。可以看出当螺纹距离轴肩圆弧较近时,两者的应力集中区域部分重合,相互影响,局部应力叠加使得此时螺纹根部的应力集中系数变大。因此,在螺纹的布置上,应适当使其距离轴肩一段距离,避免两者的高应力区重合,以减小应力集中系数。

图11 轴肩-螺纹应力云图(L=1.4 mm)Fig.11 Stress contour at the area between shaft shoulder and thread(L=1.4 mm)
5 结论
以3 500 m3/h绞吸挖泥船舱内泵的模型泵的轴端梯形螺纹为研究对象,在ANSYS中建立了泵轴端部二维轴对称参数化模型,采用有限元方法计算了在轴向拉伸载荷作用下螺纹根部的应力集中系数,分别讨论了螺纹根部倒角半径r、螺纹牙高H、螺距P以及螺纹位置对螺纹根部应力集中系数Kt的影响,主要得到以下结论。
(1)泵轴梯形螺纹根部应力集中系数比轴肩处大。对于有较大安全系数的结构而言,局部最大应力一般不会超过其屈服强度,即不会产生静力破坏;但对于承受交变载荷的结构,该处容易产生疲劳破坏,需对其疲劳寿命进行预报。
(2)在本文所研究的影响因素中,螺纹根部倒角半径对应力集中系数的影响最大,应力集中系数随倒角半径的减小而增长较快,建议螺纹根部要尽可能设置较大的圆角;螺距对应力集中系数具有线性正相关影响,应在设计规范要求范围内尽量减小螺距;螺纹牙高度对应力集中系数的影响较小,基本可以忽略。
(3)螺纹与轴肩各自产生的高应力区会相互叠加,随着两者距离的增大,相互影响减小,应力集中系数逐渐减小且趋于稳定,实际设计中可结合泵组安装尺寸要求而综合考虑、确定二者间距。
