基于EMD-LS-MFDFA法的离心泵异常振动识别

2022-12-18罗远兴胡凤城

南昌工程学院学报 2022年4期

梁兴，罗远兴，邓飞，胡凤城

(南昌工程学院江西省精密驱动与控制重点实验室，江西南昌 330099)

离心泵异常振动不仅会降低设备运行效率，缩短设备零部件使用寿命，严重时甚至迫使水泵停机。离心泵异常振动诱因较多，且大多呈现非线性非平稳特性，为离心泵故障诊断带来了一定困难。如何从异常振动信号中提取其故障特征，向来是科研人员研究的热点问题之一。譬如，尹江南[1-2]等采用时域和频域分析方法提取离心泵故障特征并证明了其有效性；周云龙[3-5]等分别针对离心泵、混流泵振动信号进行EMD分解，进而提取了水泵振动信号的特征向量；佟延文[6]对离心泵地脚螺栓松动进行频谱分析，并成功提取出相应的故障特征信息。

上述非线性分析方法在提取离心泵振动特征研究中取得了一定的成果，但随着监测水平及故障诊断要求的提高，探索并改进信号提取方法，排除实测信号不规则性和局部趋势项影响，越来越受到重视。而多重分形去趋势波动分析法[7](MFDFA)就是新出现的处理方法之一。林近山[8-9]等采用MFDFA方法有效提取出旋转机械、地震动信号的特征，李洋[10-11]等证明了MFDFA方法能够有效获取风力机组轴承、切削工具在故障状态下信号的多重分形特征；但典型的MFDFA存在局部趋势项不能准确移除的问题，为此，本文以典型的离心泵地脚螺栓松动振动信号为例，融合自动判定EMD趋势项法和最小二乘法(LS)，提出一种EMD-LS-MFDFA的多重分形分析方法，以准确提取地脚螺栓松动故障下的信号特征。

1 EMD-LS-MFDFA方法

EMD方法在理论上处理非线性非平稳信号具有非常明显的优势[12]。本文综合利用一种自动判定EMD趋势项方法[13]并结合LS拟合趋势项，使其解除EMD完全分解的限制，同时克服模态混叠和端点效应的缺陷以及有效避免原始信号对LS拟合精度的影响。

针对原始信号x(i)(i=1，2，…，N)，可用EMD法进行分解：

(1)

式中n为EMD根据自身尺度特征将x(i)分解为本征模函数(IMF)的个数；cj(i)为第j个IMF分量(j=1，2，…，n)；rn(i)为信号残余分量。

对理想信号，趋势项主要存在于rn(i)中。对实际信号而言，一些低频IMF分量也含有部分趋势项信息。因此，假定残余分量为第n+1个IMF分量，若认为原始信号的趋势项是第T个IMF分量到最后一个IMF分量的和，则其可表示为

(2)

为确定T值，引入EMD趋势项自动判定准则，可由下式表示：

(3)

理想状态下，Z=1，实际中常取Z=0.95。设自动判定后的趋势项M(i)为以f为采样频率的数列(i=1，2，…，N)，则趋势项可表示为

(4)

式中a=i/f；bk为趋势项系数，系数bk可依据最小二乘法求解。

在此基础上，可利用EMD-LS提取最终信号x′(i)为

x′(i)=x(i)-(M(i)-w(i)).

(5)

进而则针对信号x′(i)，依据MFDFA法[7]进行特征提取，即信号可表示q阶波动函数：

Fq(s)=ash(q)，

(6)

其中s为x′(i)的累积离差所划分的等长子区间长度；a为常数；h(q)为广义Hurst指数；最小二乘法拟合Fq(s)与尺度s所得斜率即为其值。h(q)随q值变化时，则是多重分形过程。

根据Legendre变换，广义Hurst指数h(q)与多重分形中的质量指数τ(q)、奇异指数α和多重分形谱f(α)有如下关系：

τ(q)=qh(q)-1，

(7)

(8)

f(α)=q[α-h(q)]+1.

(9)

2 实验装置及实验条件

实验在型号为IS50-32-125离心式循环水泵装置上进行，实验装置如图1所示。在离心泵壳和电机外壳垂直布置型号为xz860A-20振动传感器，在离心泵和电机之间分别布置型号为TH4803A扭矩传感器和XZ11转速传感器，在离心泵的前后方向各安置一个型号为ZWP-L61-K压力传感器。离心泵转速为2900 r/min，流量为11.2 m3/h，扬程为16 m，离心泵驱动机转频为50 Hz。

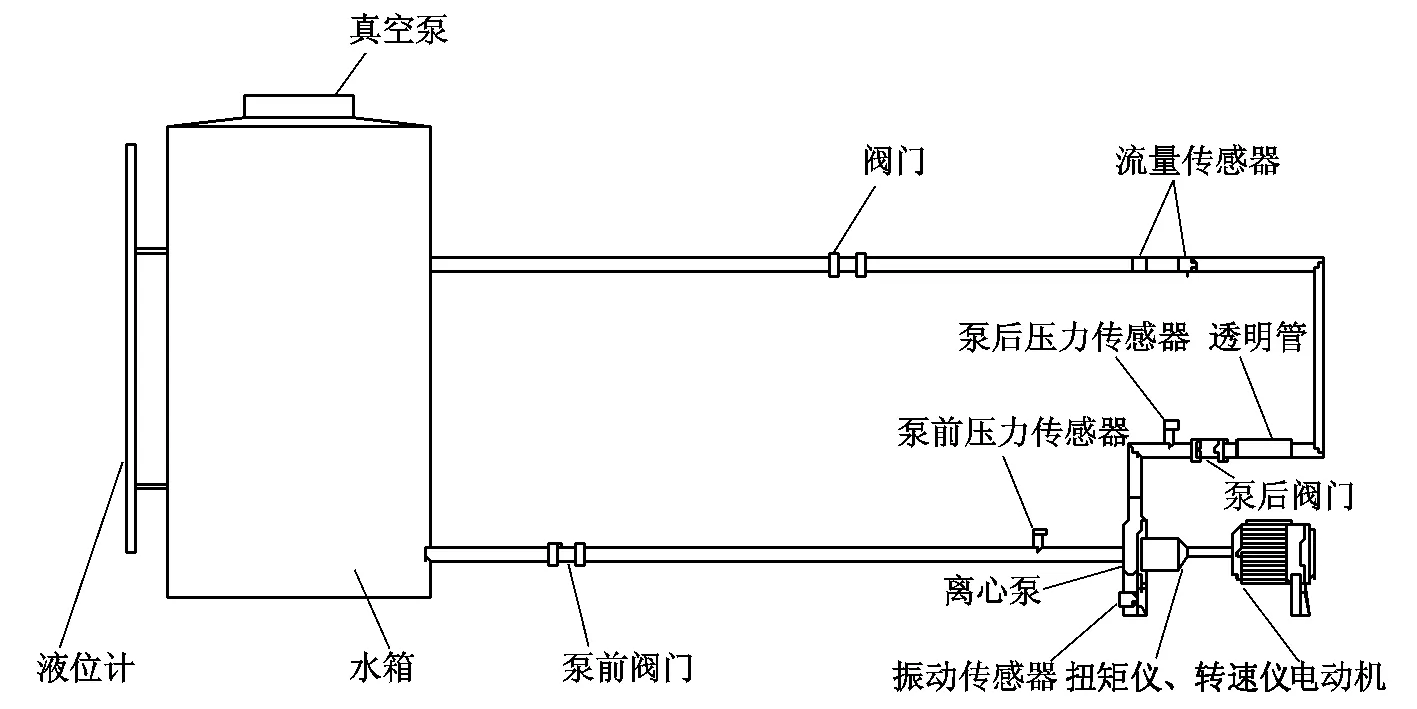
图1 实验室循环水泵装置

本次实验在离心泵正常状态和地脚螺栓松动的情况下(泵与电机固定于同一底座，松动底座AZ-70型地脚螺栓)，通过PXI-4472B型动态信号采集仪，将采样频率设为1 kHz，实测泵壳振动信号、电机振动信号、扭矩信号、转速信号以及泵进出口压力信号。图2为各类信号正常状态与螺栓不同松动状态时信号波形图。

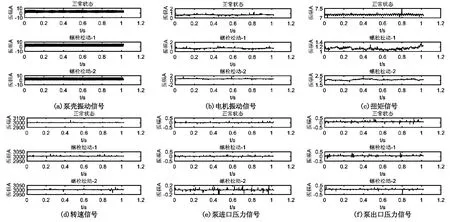
图2 各类传感器信号时域图

3 地脚螺栓松动的实例分析

以离心泵振动信号为例，选取两组地脚螺栓松动程度不同的数据，利用HHT进行时频分析如图3所示。由于内在动力学机制的不同，不同故障信号拥有不同的频率范围，其能量分布也各有不同，而从图3(a)和图3(b)两组螺栓松动故障的时频图可知，故障信号经HHT变换后虽能在一定程度上分离出信号的频率且能量值有部分差异，但两组信号能量值整体差异不明显且频率接近，区分度较差，并且HHT的核心部分为故障信号的EMD分解会存在模态混叠现象，导致时频图不能够准确表示信号随频率的不同变化，不利于准确诊断其故障。

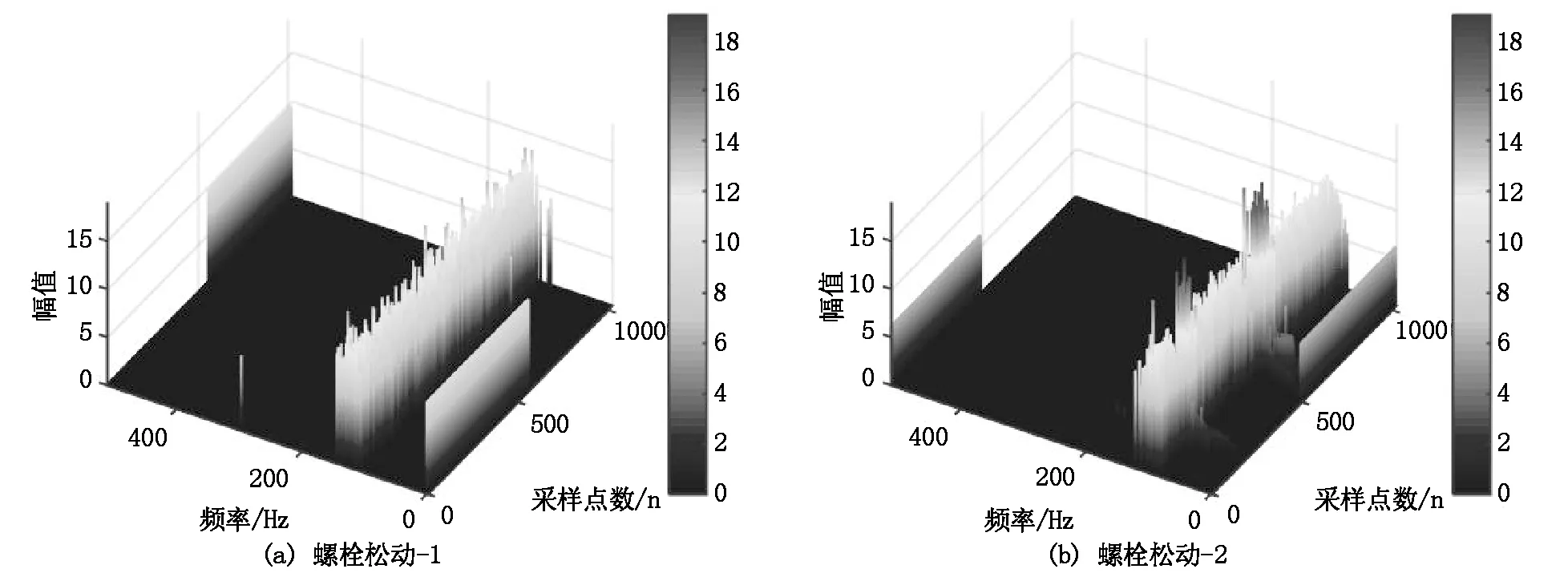
图3 螺栓不同松动故障信号HHT三维时频图

为此，仍以离心泵振动信号为例，以一组离心泵正常状态、两组地脚螺栓松动程度不同的离心泵振动信号进行EMD-LS-MFDFA方法分析。设定数据长度，参数s最小值为4，最大值为256，以8为间隔取32个值，参数q最小值为-10，最大值为10，采用EMD-LS-MFDFA方法进行分析，分析结果如图4所示。

图4(a)为不同状态下的离心泵振动信号q阶质量指数关系图。从图4(a)可知，当离心泵处于正常状态时，质量指数τ(q)与q之间呈近似线性关系，而离心泵地脚螺栓松动时，质量指数τ(q)与q之间存在转折点，呈典型非线性关系，说明地脚螺栓松动状态下引起的离心泵振动信号的多重分形特性强于正常状态，而地脚螺栓不同松动状态下的多重分形特征也有明显区别。因此EMD-LS-MFDFA方法能够分辨离心泵的运行状态。

图4 EMD-LS-MFDFA方法处理不同状态下离心泵振动信号的结果图

图4(b)为不同状态下的离心泵振动信号q阶广义Hurst指数关系图。从图4(b)可知，因内在动力学机制的不同，离心泵处于正常和地脚螺栓松动两种状态下的广义Hurst指数具有极大的差异。离心泵地脚螺栓松动时，广义Hurst指数h(q)是一条随q增大而减小的函数。

图4(c)为不同状态下的离心泵振动信号多重分形谱的关系图。从图4(c)可知，离心泵运行的状态不同导致的多重分形谱曲线明显具有不同的形状、位置和值域，但多重分形谱曲线均是一条随奇异值α变化的单峰曲线，说明离心泵不同状态下的振动信号具有不同的多重分形特性。根据α和f(α)，获取离心泵两种状态下的多重分形谱参数即多重分形谱宽度Δα、多重分形谱差值Δf以及对应fmax(α)时的奇异值α0，其结果如表1所示。其中，Δα越大，表明信号的多重分形特征越明显，信号波动越剧烈；Δf能反映信号波动剧烈峰值与波动平稳峰值所占比例，比例越大，信号波动性越大；α0越大，信号的不规则程度越高。因此分析表1可知，两组离心泵地脚螺栓松动状态时的多重分形谱特征参数Δα、Δf和α0均大于正常状态值，表明EMD-LS-MFDFA提取的特征参数对地脚螺栓松动状态的变化非常敏感，能够区分正常和故障状态。

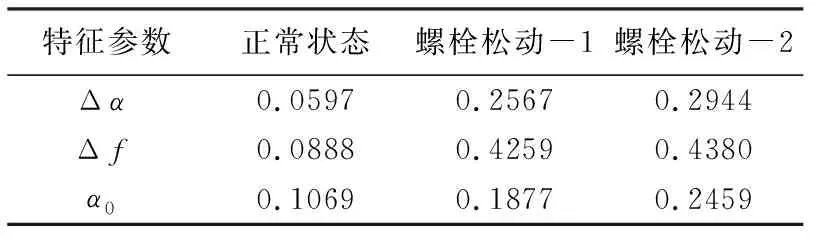
表1 离心泵振动信号特征参数

为验证EMD-LS-MFDFA法信号分析的稳定性，将不同状态下的离心泵振动信号各自选取10段，每段的数据长度为1 024，运用EMD-LS-MFDFA获取每一段离心泵振动信号的特征参数，如图5所示。显然，正常状态和螺栓松动的离心泵振动信号明显分布在不同的区域内，表明本文方法所提取的特征参数Δα、Δf和α0能够有效的区分正常信号与故障信号，具有较好的稳定性。

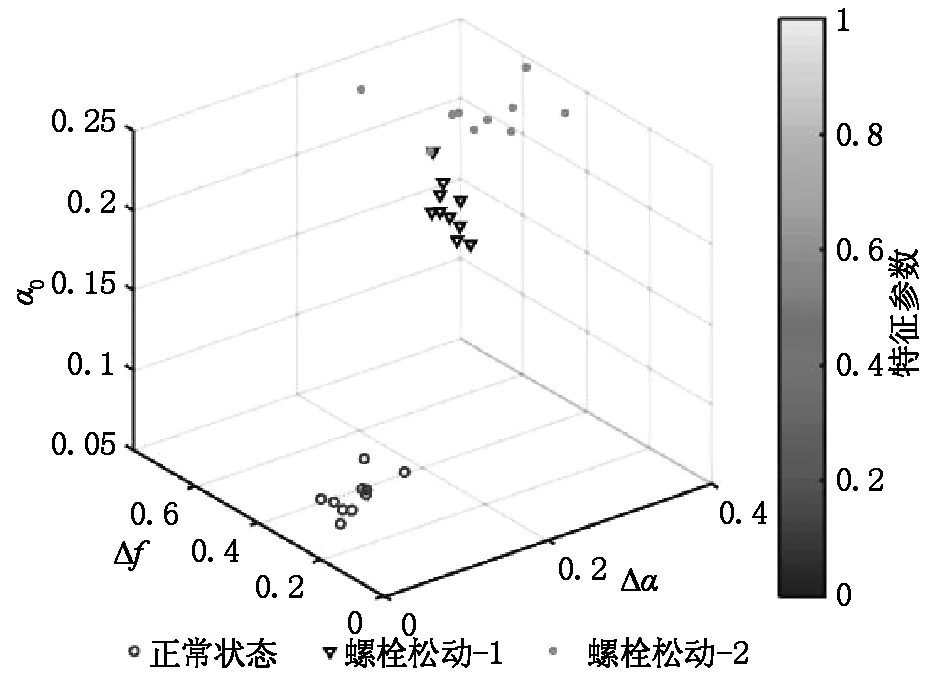
图5 不同状态的离心泵振动信号Δα-Δf-α0图

利用同样的方法，对一组正常状态和一组螺栓松动的离心泵振动信号、电机振动信号、扭矩信号等各自分成4段进行处理，每段数据长度为1 024。通过分析可知，EMD-LS-MFDFA法能够准确处理离心泵振动信号、电机振动信号、扭矩信号，信号的特征参数值如表2所示，由此获取的信号均值以及均方差列于表3。

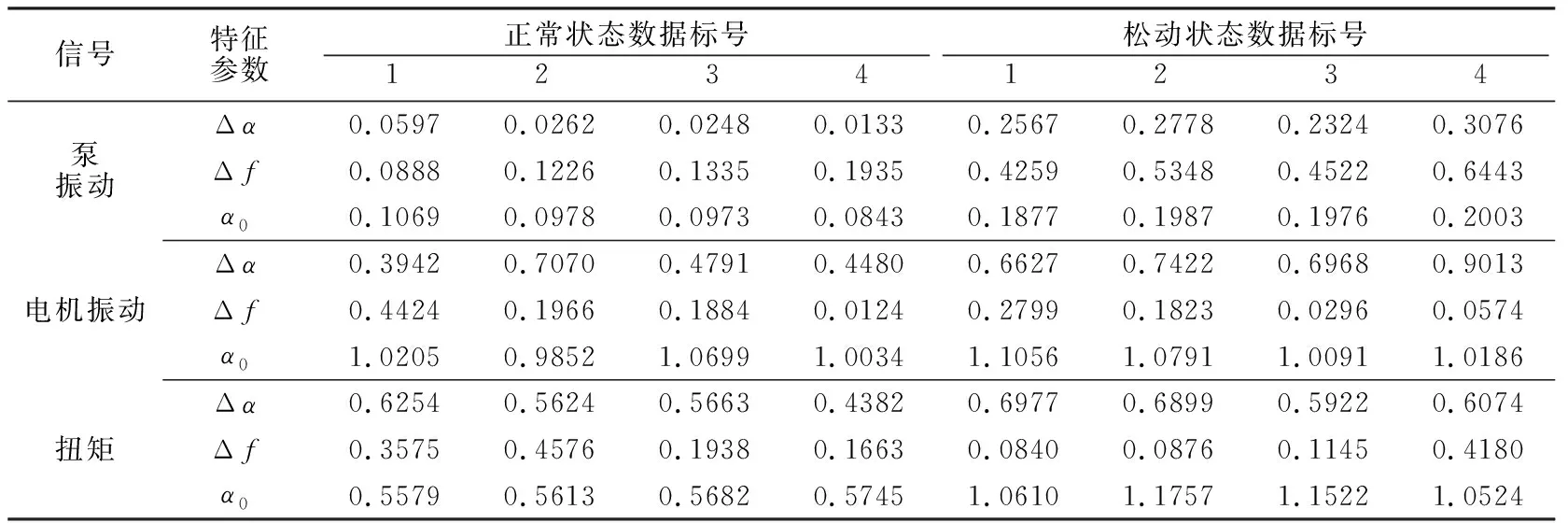
表2 不同信号类别特征参数

由表2～3可知，正常状态下的离心泵振动信号、电机振动信号、扭矩信号的Δα和α0值总体小于松动状态值。特征参数Δα和α0的均方差较之Δf而言更小，说明Δα和α0具有较好的稳定性，并且除离心泵振动信号外，余下2类信号的Δf值存在多处交叉的情况，因此Δf值区分度较差。综合分析可知，地脚螺栓松动对离心泵造成较大的影响，对电机、扭矩仪等测点位置的影响相对较小。