面向碳中和的电力系统复杂谐波信号检测方法

刘雪强, 焦雅琼

(国网西藏电力有限公司，西藏 拉萨 850000)

0 引 言

自2021年以来，“碳中和”一直被视为年度重点任务，为电力资源的合理配置提出新的依据[1-3]。国家电网贯彻落实了该项发展理念，启动了首个绿色技术交易中心，实现面向碳中和的电力系统变革[4]。但此背景下的电力系统产生了大量复杂谐波，干扰电力系统的正常运行。

针对这一问题已有相关学者进行了研究，文献[5]利用经验小波变换预处理信号，通过分离各次谐波与基波信号，利用正负成对的高斯白噪声抑制模式的混叠现象，获取各次谐波的幅值、频率以及扰动起止时刻，有效实现了多频谐波信号的自适应分解。文献[6]采用FFT算法确定小波分解的频带和层数；利用小波变换分解信号；采用小波重构的算法检测电力系统中的谐波、间谐波的详细参数。

以上方法只适用于背景均匀的检测环境，针对复杂谐波信号的位置预测不到位，非均匀背景下的检测结果依旧被背景信号覆盖。基于此，研究全新的电力系统复杂谐波信号检测方法。基于压缩感知重构谐波信号数学模型，采用扩展卡尔曼滤波器求解最优权值，检测均匀背景中的谐波信号，构建Hankel矩阵；采用非递归型滤波器，检测非均匀背景中的谐波信号。设计对比试验证明本文方法能够清晰检测非均匀背景下的微弱谐波信号，保证检测方法适用于均匀和非均匀背景。

1 电力系统复杂谐波信号检测方法

1.1 基于压缩感知重构谐波信号

在正交变换域中，电力系统的谐波信号具有稀疏性特征，设配电网构建电力系统的谐波信号数学模型为：

(1)

式中：x为谐波信号；N为模型中包含的谐波分量总数；Ki为第i次谐波的幅值；fi为谐波频率；λi为基波的初始相位。提取上述公式中的谐波分量fi(x)，利用离散傅里叶变换(DFT)进行变换，得到：

(2)

(3)

(4)

式中：ε为偏移量，取值在-0.5～0.5之间；o为幅度谱线数量。基于上述过程，描述信号的稀疏性，根据该结果进行信号重构。

将谐波信号设置为x=(x1,x2,…,xn)，利用测量矩阵W采集其中的m个值，该过程通过下列公式实现：

y=Wx

(5)

式(5)为线性测量结果，利用矩阵实现对信号的降维采样。根据式(4)对信号稀疏性特征的描述，对上述公式进行转化，实现基于压缩感知的谐波信号重构。

y=Wx=Wμφ=Wμ·φ

(6)

式中：Wμ为感知矩阵。利用测量矩阵获取观测向量，得到公式(5)的计算结果。在重构谐波信号以获得矢量后，生成新信号以完成原始信号的重构，得到压缩后的复谐波信号，公式为：

x′=arg min‖x‖

(7)

式中：‖x‖为向量的范数，也就是非零元素的个数。将式(6)作为信号重构算法的运行约束条件，利用上述计算过程得到重构的原始信号。

1.2 检测复杂谐波信号

1.2.1 检测均匀背景中的谐波信号

针对均匀背景中的谐波信号，采用扩展卡尔曼滤波器(EKF)求解最优权值，实现对目标信号的检测。

首先，计算最优滤波器输出与0信号之间的均方误差，得到：

MSE=E(0-yω(n)2)

(8)

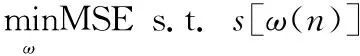
ω(n)=θω(n-1)+α(n)

(9)

式中：θ为≤1的常数值；α(n)为噪声向量；s为设置的检测条件。

其次，根据上述公式建立测量方程为：

(10)

式中：α1(n)、α2(n)分别为剩余误差和与约束条件相关的误差。

最后，以保证待检测信号不失真为前提，将滤波器输出调整到最小，得到协方差。将式(9)代入式(8)，得到协方差公式为：

(11)

根据式(10)和式(11)，让算法反复迭代更新滤波器权值，实现对信号与干扰加噪声比(SINR)结果的输出，公式为：

(12)

根据式(12)结果，从均匀背景中检测复杂谐波信号，得到目标信号。

1.2.2 检测非均匀背景中的谐波信号

针对非均匀背景中的谐波信号，假设观测信号x中包含弱谐波信号和强谐波信号，则构建Hankel矩阵输出待检测信号的值，公式为：

y=[y(A),y(A+1),y(A+n)]T

(13)

式中：n为待检测信号尺寸；A为滤波器阶数。在非均匀背景中利用上述公式将观测信号拆分成多个字段，建立全新的数据序列。在此环境中使用的滤波器为非递归型滤波器(FIR)，该滤波器根据谐波信号的幅度和相位得到谐波的幅度值，公式为：

(14)

式中：β为谐波复幅度；γ(y)为目标值；H(y)为非均匀背景信号的协方差矩阵；p(y)为待检测信号的谐波成分；q(y)为信号频率向量。根据上述结果计算FIR的SINR，得到：

(15)

根据式(15)输出结果，检测出目标谐波信号。

至此，在均匀背景、非均匀背景中，实现面向碳中和的电力系统复杂谐波信号检测。

2 实例测试

2.1 采集复杂谐波信号

选择A市目前应用于配电网的电力系统作为测试数据来源。构建一个电力系统复杂信号模型，如式(16)所示，基于该电力系统中存在的基波、稳态谐波、间谐波和高频暂态衰减谐波，设置复杂谐波环境。设置稳态谐波的频次为2、4、6以及10次，基波和稳态谐波对应的比例为100 ∶50 ∶50 ∶20 ∶20。设置间谐波幅值比为10 ∶8 ∶5 ∶1，设置高频暂态衰减谐波的初始位置在0.04 s处，且最大幅值为60 V。模型可以通过式(16)描述：

(16)

式中：f为信号；d为时间参数。根据上述模型模拟电力系统的复杂谐波信号，得到的信号原始波形如图1所示。

图1 电力系统复杂谐波信号波形仿真结果

国际检测要求谐波检测次数要达到60次，因此将检测方法的采样频率设置在3～5 kHz之间，检测不同背景中的复杂谐波信号。

2.2 重构谐波信号

本文检测方法与基于经验小波变换的检测方法分别按照各自的手段描述谐波信号稀疏性特征，根据得到的结果重构谐波信号。图2为两组方法对复杂谐波信号的重构结果。

图2 复杂谐波信号重构结果

由图2所示，传统方法的高频暂态衰减谐波检测结果存在误差，尽管最大幅值满足60 V，但起始时刻不是0.04 s。本文检测方法对高频暂态衰减谐波信号的重构效果较为精准，高频暂态衰减谐波检测结果的最大幅值为60 V，且谐波的初始位置在0.04 s处。

2.3 结果分析

2.3.1 均匀背景中的检测

均匀背景即电力系统处于非线性状态，更改电力系统复杂信号模型如下：

(17)

图3 复杂谐波信号检测结果

令式(17)中的参数σ为10、参数r为30、参数k为2.66。设置a、b、c的初始值为0.1。分别利用两组检测方法进行复杂谐波信号检测，测试结果如图3所示。

由图3可知，传统方法与本文检测方法均得到了复杂谐波信号当中的1组弱信号，说明在均匀背景中，两组方法均有较好的检测效果。

图4 复杂谐波信号检测结果

2.3.2 非均匀背景中的检测

非均匀背景即电力系统处于线性状态，更改电力系统复杂信号模型如下：

(18)

令式(18)中的参数σ为0.2、参数r为0.4、参数k为5.8。同样设置a、b、c的初始值为0.1，得到非均匀测试背景。分别利用两组方法在非均匀背景下检测复杂谐波信号，测试结果如图4所示。

由图4可知:在非均匀背景中传统方法检测的弱谐波信号，在0.100 7 Hz处，被大量的谐波信号所覆盖，因此在这种环境下，传统的检测方法可能无法检测到复杂谐波信号中掺杂的微弱信号；而本文检测方法得到的微弱谐波信号为0.087 3 Hz，微弱谐波信号检测清晰，背景中的复杂信号不覆盖微弱谐波信号，保证其适用于均匀和非均匀背景。

3 结束语

针对谐波信号的多样化特征，设置均匀背景和非均匀背景两个条件。利用扩展卡尔曼滤波器和非递归型滤波器，输出重构后的电力系统复杂谐波信号。提出电力系统复杂谐波信号检测方法，获得更准确的谐波信号。为复杂谐波信号检测提供更准确的数据，检测复杂谐波信号中夹带的弱信号，从而为电力系统的使用提供更科学的检测方案，实现碳中和背景下电力工业发展的技术支持。