考虑DG与负荷时变性的配电网分时段动态重构

黄曜，林凌雪，管霖

(华南理工大学 电力学院，广东 广州 510640)

0 引 言

配电网重构通过改变开关状态来调整网络的拓扑结构，完善功率传输，是配电系统降损有效的方法之一。由于配电网合环转供电方式的逐渐普及与分布式电源(distributed generators，DG)的大量接入，重构操作须考虑开关的动作限制及网络节点功率的时变性，尽量减小合环冲击与功率波动对配电网带来的影响。配电网动态重构通过时段划分，将动态问题转化为不同时间段的静态重构问题进行求解[1],避免开关的频繁开闭，更能体现负荷与DG的时变性,更符合工程实际。

目前已有大量基于时段划分的配电网动态重构求解方法。文献[2]以递归聚类方法遍历时段划分方案，再利用“拐点法”确定最优时段划分数，但方法本身会使时段划分数过多。文献[3]以马氏DTW距离为衡量时段间负荷相似程度的依据，并依此进行时段划分，但缺少一种最优时段数的确定方法。文献[4]用模糊C均值聚类法进行时段划分，但该方法无法按时序进行划分，会使初始分时段数过多，需要进行类别融合，导致过程繁琐，且最优类别数需预先给定。文献[5]先对单位时段作静态重构，再根据降损参数合并时段，但该方法需要大量重复运算。总体而言，主流重构时段划分方法较为繁琐且效果欠佳。

区间数能反映DG及负荷的不确定性，文献[6]用仿射数表示区间数，并将仿射潮流方程进行泰勒展开，使复杂的仿射方程转为确定性潮流求解。

本文依据DG和负荷的时变性，建立等值负荷预测曲线，利用垂线测距法确定最优分时段方案。构造以区间网损最低为目标的重构优化模型，采用仿射方程表示不确定量，以仿射泰勒扩展的潮流计算方法进行潮流计算，并采用改进十进制粒子群算法求解重构模型。

1 基于垂线测距法的重构时段划分

1.1 损失函数与相似度指标

1) 相似度指标

预测DG出力，负荷功率大小，以“负的负荷”表示DG出力，叠加并构造等值负荷曲线。将单位时段功率值抽出，构成以时间数为行，节点序号为列的数据矩阵，矩阵元素对应于不同时段各节点的功率。将全时段划为N个单位时段，构成矩阵H=[H1,H2, …,HN]T。单位时段i下各节点功率Hi=[hi1,hi2, …,hin]。式中：n为节点数；hij为第i个单位时段下节点j的复功率。定义相邻时段间负荷值的欧式距离为段差，并以此作为“相似度指标”，计dpi(i=1,2,3,…，N-1)为第i+1时刻与第i时刻所构成的段差值。

(1)

段差值dpi即相似度指标大小能够反映单位时段间负荷的变化程度，遍历所有段差值构成一个段差列向量D。

D=[dp1,dp2, …,dp(N-1)]T

(2)

2) 优势性分段准则

相似度值越大，越应该进行重构操作；定义优势性分段准则，令Dmax.k(k=1,2,…，N)为D中最大的部分元素所对应的段差集，k值对应分时段数，决定了Dmax.k中的元素数量。当k=1时，Dmax.k为零集，有：

Dmax.k∈D

(3)

时段划分以Dmax.k中所对应各元素的相关时段为分时段点，分时段操作后Dmax.k归零。遍历所有可能的分段方案，并将每次D中的所有元素相加得到总段差；形成N个分段方案，不同分段方案的总段差形成一个损失函数列向量S：

S=[s1,s2, …,sN]T

(4)

1.2 基于垂线测距法的最优时段划分

以图1为例对垂线测距法进行步骤分解。

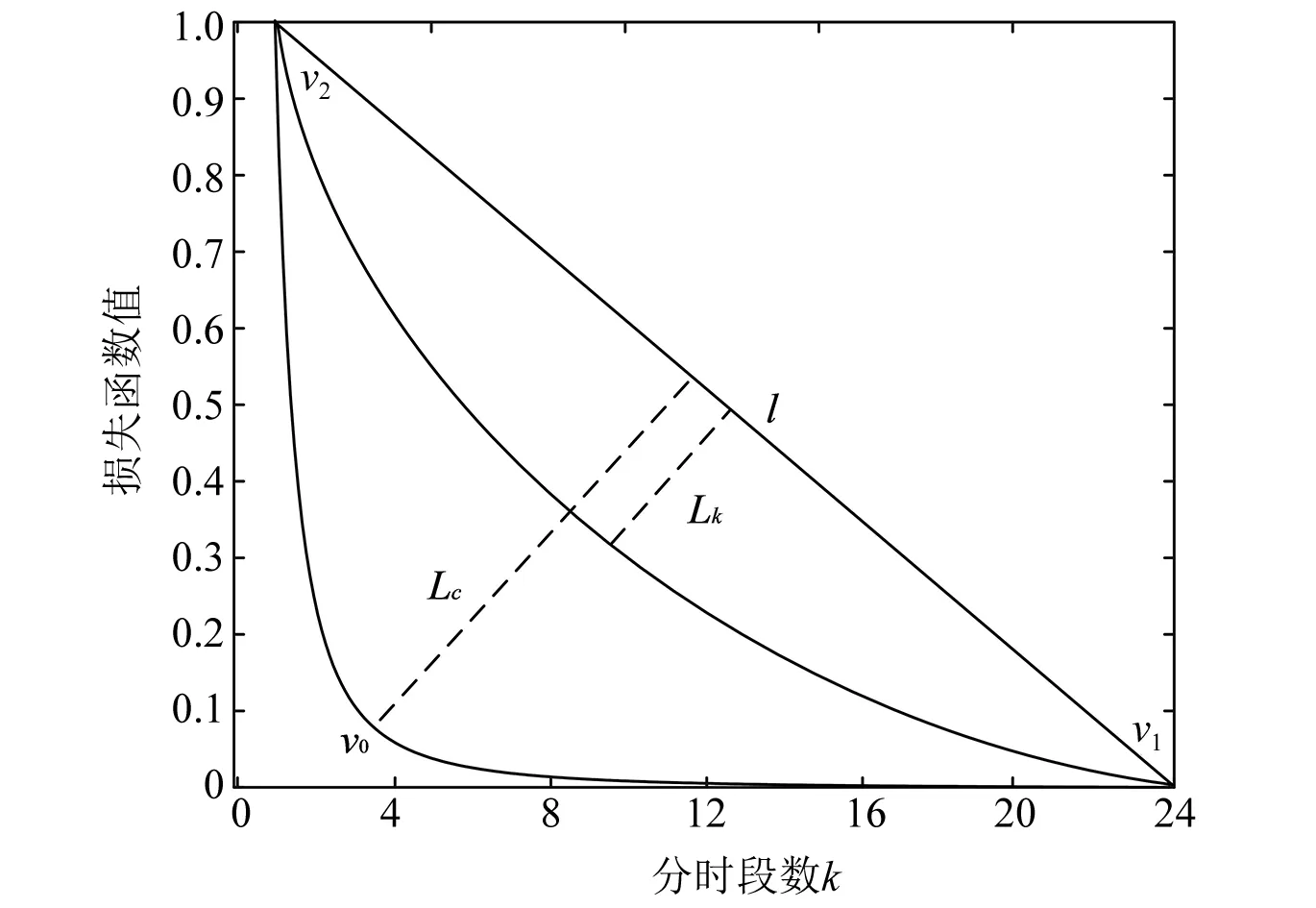
图1 垂线的渐进收敛过程

步骤一，设分时段的总数为24，横轴对应分时段数k，纵轴为以优势性分段准则所得损失函数S对应的元素Sk，可得S[si(N,k)]关于分时段数的近似曲线。

步骤二，连接最大损失函数值对应的点v2与最小损失函数值对应的点v1，得到一条直线l。选择曲线的拐点v0作为局部最优分段点，并记录该点对应的最大垂线距离Lc，由于横轴的单位步长量相同，可通过纵坐标损失量大小的比较找到该点的位置。

步骤三，由步骤二所得拐点v0对应的相似度值可能为“相对接近”非“最接近”，从而导致时段划分数过多。拐点到直线l的垂直距离能够反映曲线的均匀度，将其作为评价指标，找到该垂线距离随分时段数减小过程中变化幅度刚好变小的拐点并将其作为最优分时段点。按步骤二继续进行分段，使分时段数向1逼近，并记录每次的局部最优分段点到l的垂线距离Lk，当分段数为1时停止分段，此时L0=0。

以图1为例的垂线距离Lk可通过公式表示为：

(5)

式中:Sk为分段数k对应的损失函数值。

步骤四，将所遍历的垂线距离表示为一个向量集合：

LK=[L0, …,Lc]

(6)

将LK中的元素从大到小排序并按步骤一、二作出LK关于排序号的变化曲线，以相同方法连接首序号与末序号坐标点，构成直线l′,再找到此时垂线变化曲线上距离l′最远的点，此点便为最优时段划分点。

2 重构模型的建立及算例分析

为表达DG与负荷的不确定性，建立所有时段区间网损最小的目标函数：

(7)

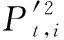
以仿射值替代区间数表示DG和负荷的不确定性出力，即：

(8)

(9)

式中:PDG.r、QDG.r及PL.r、QL.r分别为DG有功、无功出力及负荷有功、无功大小的区间半径；PDG.c、QDG.c及PL.c、QL.c分别为DG有功、无功出力及负荷有功、无功大小的区间中值；ε为噪声项。

重构过程除必要的电压、DG出力、馈线功率及辐射状网架约束外，还加入了开关的动作次数上限约束：

Ntotal≤Ntotal.max

(10)

式中：Ntotal为开关动作总次数。

仿射变量直接代入潮流会造成大量冗余项，采用仿射泰勒扩展的潮流计算方法防止仿射方程迭代，增加求解效率与求解精度。最后，用改进十进制粒子群算法[7]进行重构求解。

图2为网络重构流程。

3 算例验证

3.1 时段划分

通过如图3所示的IEEE 33节点系统进行仿真，设基准电压为12.66 kV，基准功率为10 MW。将整时段划分成24个单位时段，以垂线测距法得最优划分时段数为4；将等值负荷曲线以时段数求平均值并叠加DG出力得到单位等值负荷曲线，如图4所示(虚线对应时段划分点)。

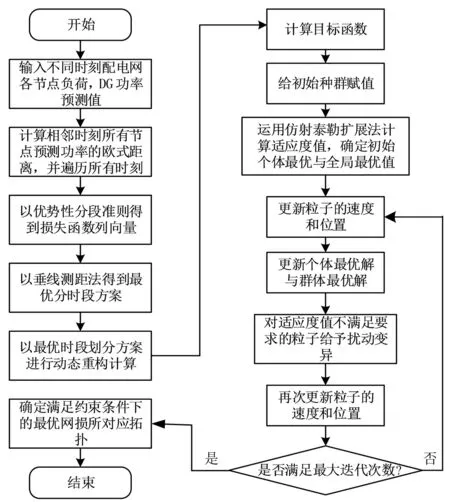
图2 重构流程图

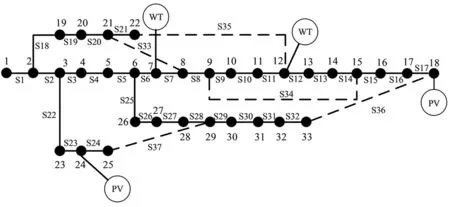
图3 IEEE 33节点系统

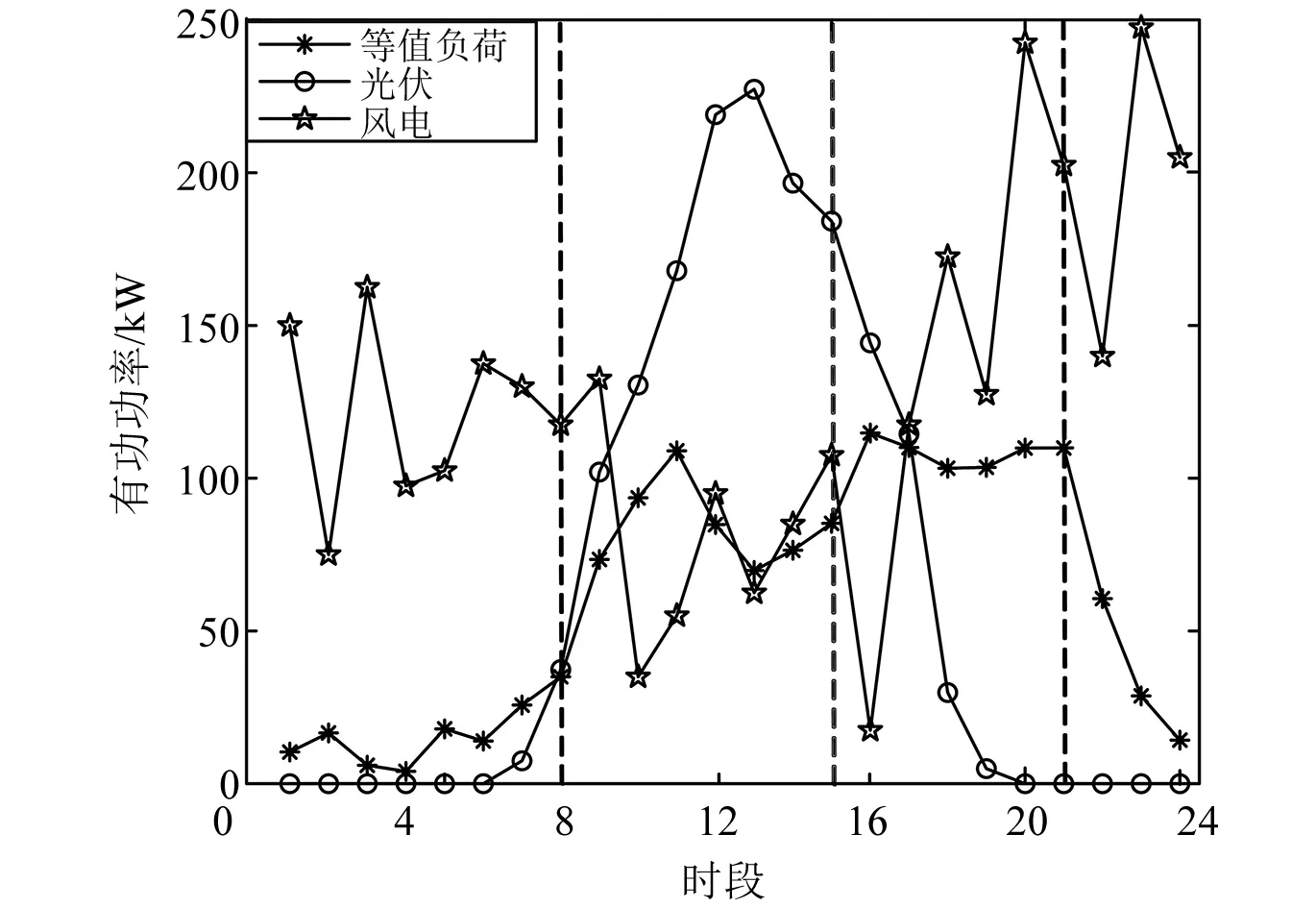
图4 单位等值负荷曲线

3.2 最优重构方案

以改进十进制粒子群算法做动态重构计算，以联络开关为起点构造基本环代入重构解集进行回路寻优，避免盲目搜索；引入扰动变异，防止陷入局部最优；最大迭代次数设210次，开关上限18次，DG与负荷预测误差±10%。分别以三种方法进行重构计算并通过表1来表示计算结果。方法一对每个单位时段作全时段静态重构；方法二采用文献[2]中方法进行动态重构；方法三为本文垂线测距法时段划分的动态重构。

由表1可知，未重构网络的整体网损值最高。全时段静态重构使得整体网损值最低，但开关开断频次最高，由于未进行分时段操作，因此其时段划分耗时为0。方法二、方法三均进行了时段划分，从而减少了开关动作次数与重构计算,并得到了重构最优解。

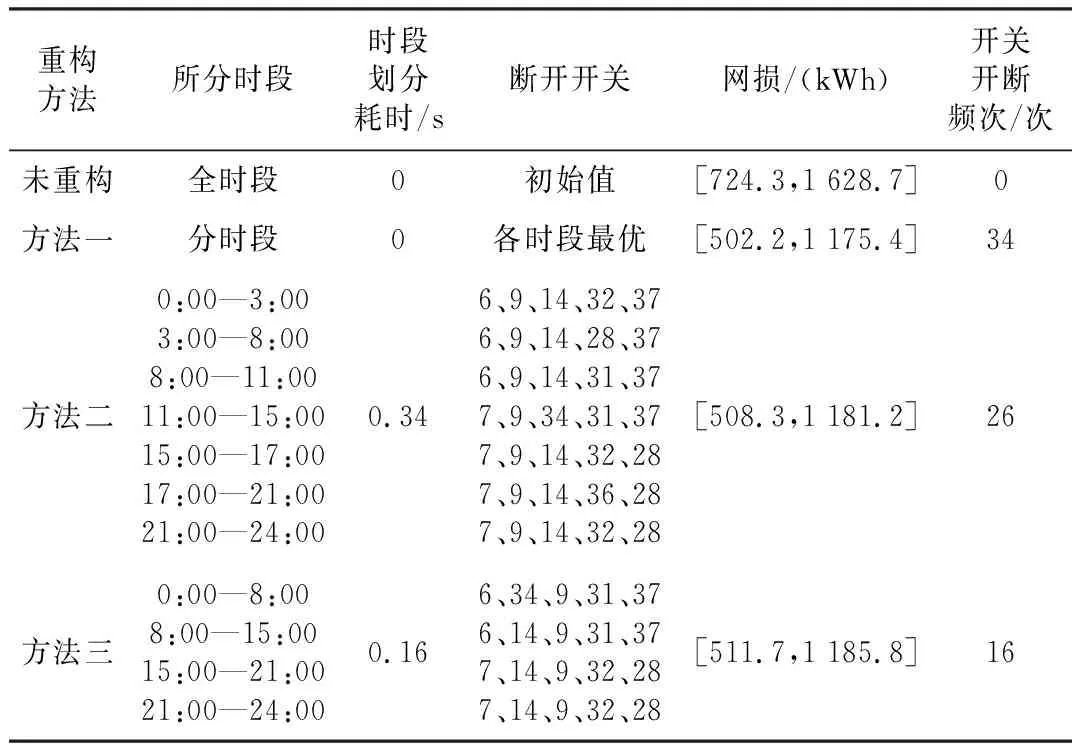
表1 不同方法比较

方法二、方法三的时段划分数分别为7与4；重构次数分别为7与3。方法二相比方法三，网损仅有略微降低，然而开关动作次数过高，重构次数过多；方法三分段少，耗时小，并大幅降低了网损与开关动作频次。

图5为分别以基本环为解域寻优的改进粒子群算法与随机初始解寻优的改进粒子群算法进行迭代所得曲线收敛图，可以看出前者的收敛速度远快于后者。

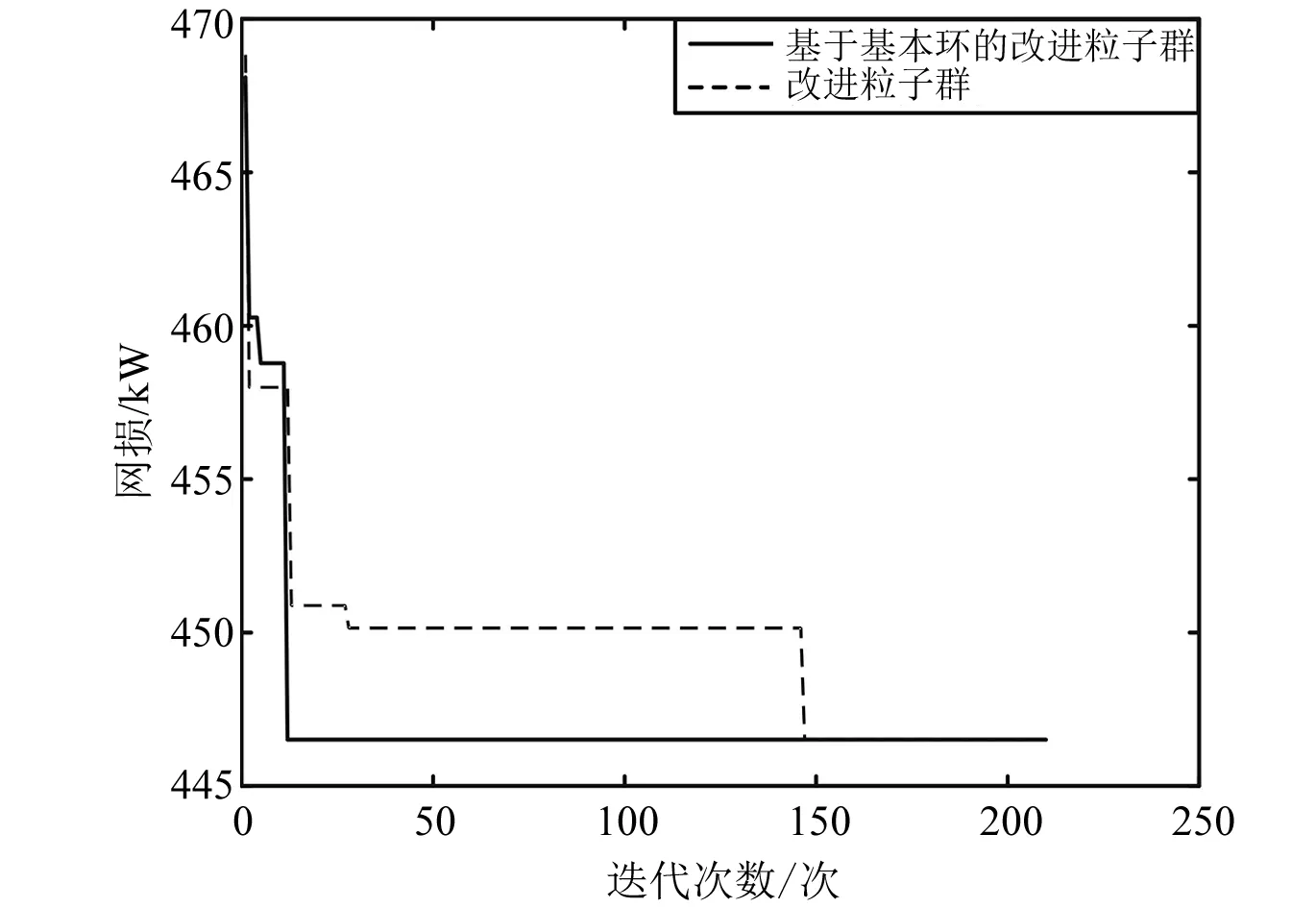
图5 算法对比

抽取单时段用Krawczyk迭代法进行一次潮流计算。如图6所示，利用本文方法所得电压区间比Krawczyk迭代法所得区间更小，但又严格包络了蒙特卡洛法所得区间。说明本文方法减小区间保守性同时保持了区间的完备性。

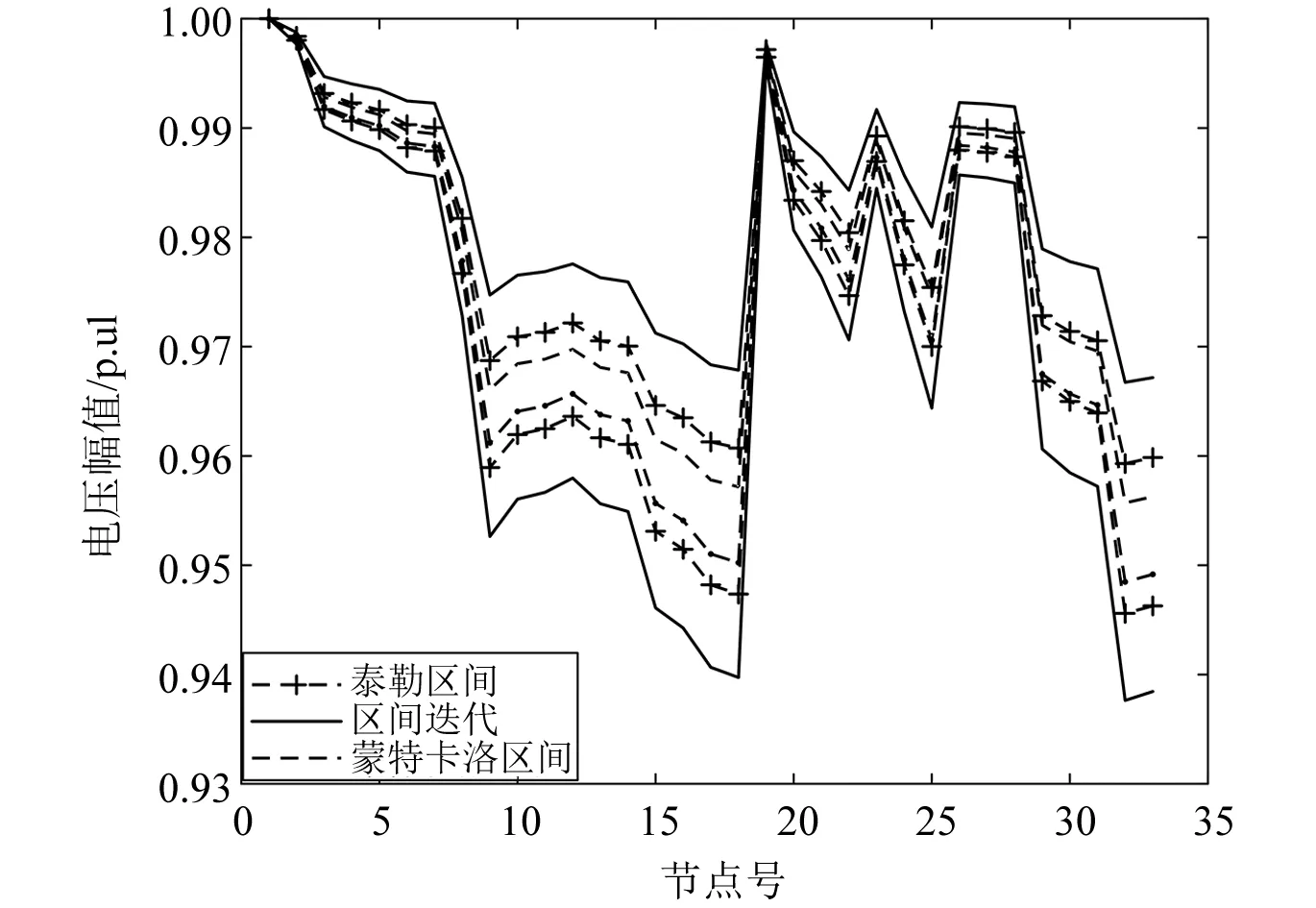
图6 不同方法区间电压幅值对比

4 结束语

本文考虑负荷功率与DG出力的时变性进行配电网多时段动态重构，相比只计及单时间断面的静态重构，更加贴近工程实际；提出垂线测距法进行动态重构时段划分。通过对比验证，证明了所提方法更加简便易行，且能更好把握时段划分的“度”，在尽可能减少重构次数的前提下大幅降低了配电网运行网损与开关〗动作频次；同时，以区间值表示功率预测误差，利用泰勒仿射扩展潮流法进行计算，使所得网损区间更加贴近实际区间。因此，本文方法具有较好的实用价值。

未来将结合需求侧响应、分时电价等因素，研究更为复杂情形下的网络动态重构策略。