基于改进风力驱动优化算法的最大功率点跟踪控制研究
2022-12-17时语欣刘鸿鹏张伟
时语欣, 刘鸿鹏 ,张伟
(东北电力大学 电气工程学院 现代电力系统仿真控制与绿色电能新技术教育部重点实验室,吉林 吉林 132012)
0 引 言
为了充分利用光能,需要研究最大功率点跟踪(maximum power point tracking,MPPT)技术,有效预测和跟踪光伏阵列的最大功率点,使光伏系统工作在最大功率点处[1-2]。
传统MPPT方法有扰动观察法(perturbation and observation,P&O)和电导增量法,虽然可以成功跟踪最大功率点,但跟踪速度和精度无法兼得,且存在振荡和误判问题[3-4]。因此,设计合理的步长是优化传统MPPT方法的关键。文献[5]提出了分区定步长的P&O法,将输出电压-功率特性曲线分为四个区域,可以有效改善跟踪速度,同时降低稳态后的功率波动。文献[6]提出了基于模拟退火和混沌理论改进的粒子群算法,结合模拟退火算法可以快速跳出局部最优解。文献[7]提出的混合MPPT法,可以有效减少搜索区域,得到更快的收敛速度。上述的混合MPPT方法解决了跟踪精度问题,但是实现复杂。
针对跟踪速度和精度的权衡问题,本文将风力驱动优化(wind driven optimization,WDO)算法与MPPT控制结合,针对光照条件突变的情况,解决MPPT算法跟踪精度差、跟踪速度慢以及适应性不强等问题。
1 光伏阵列的输出特性分析
光伏阵列的输出特性是非线性,且温度和光照强度是影响其输出的两个重要因素。为了研究温度和光照强度对光伏阵列输出特性的影响规律,可以先保持一个影响因素不变,而不断改变另一影响因素,观察其对输出特性的影响来进行研究。
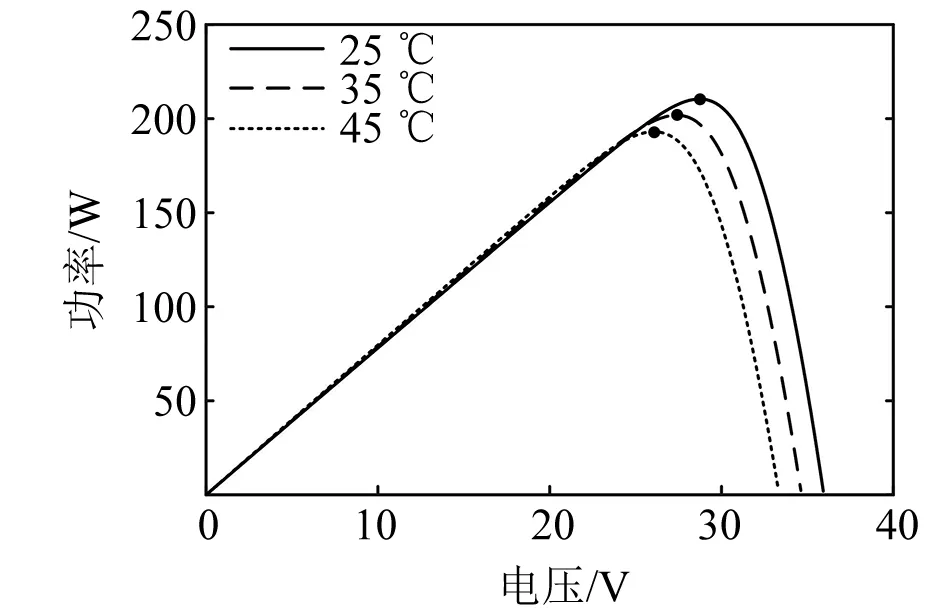
图1 不同温度下的U-P特性曲线

图2 不同光照强度下的U-P特性曲线
不同温度与不同光照强度下的U-P特性曲线如图1、图2所示。由图1和图2可知,当温度不断升高时,功率输出特性曲线有向下的移动趋势,即温度升高,光伏阵列输出的最大功率减小,但变化较小;当光照强度不断增强时最大功率输出特性曲线有明显向上的移动趋势,即光照强度增大,光伏阵列输出的最大功率也明显增大。由上述分析可知,光伏阵列的输出功率受光照强度的影响较大,而受温度的影响较小。
2 MPPT控制算法
光伏阵列最大功率点会随着温度和光照强度的变化而变化,且始终是唯一的。系统可以通过MPPT控制技术,在外界条件变化下,使系统始终工作在最大功率点处。
2.1 WDO算法
WDO算法是一种新兴的基于群体迭代的启发式全局优化算法[8]。该算法来源于对空气质点在大气中运动过程的模拟,空气质点在大气中会受到不同力的作用,开始时由于受力不平衡导致其不断地流动,最终受力平衡保持在一个稳定状态。
在WDO算法中,空气质点主要受到以下四个力的作用:重力(FG)、气压梯度力(FPG)、科里奥利力(FC)和摩擦力(FF)。其中,FG始终指向坐标原点,FPG由高压指向低压,FC指在当前维度空气质点受其他维度的影响。
由牛顿第二定律得:
ρa=∑Fi
(1)
式中:ρ为空气质点密度;a为加速度;Fi为作用在空气质点上的力。
由理想气体定律得:
P=ρRT
(2)
式中:P为空气压力;R为理想气体常数;T为温度。
空气质点在运动过程中所受四种力作用:
FG=ρδVg
(3)
FPG=-∇PδV
(4)
FC=-2Ω×u
(5)
FF=-ραu
(6)
式中:δV为空气质点的有限体积;∇P为FPG;Ω为旋转体系的角速度;u为空气质点的速度;α为摩擦因数。
由速度与加速度关系得:
(7)
将式(3)~式(7)代入式(1)得:
(8)
设定Δt=1,且设定空气质点的有限体积为1,则:
ρΔu=ρg+-∇P+-2Ω×u+-ραu
(9)
根据式(2),将密度ρ用压力方程进行替换得:
(10)
式中:Pcur为当前位置空气质点的压力值。
式(10)可进一步化简:
(11)
式中:unew为下一次迭代空气质点速度;ucur为当前位置空气质点速度;Popt为当前最优压力值;xopt为当前最优空气质点位置;xcur为当前空气质点位置。
将式(11)代入式(10)得:
(12)
xnew=xcur+unew×Δt
(13)

2.2 AWDO算法
FG和FC在寻优初期可提高空气质点的多样性和收敛速度,而寻优后期始终指向坐标原点的FG会给寻优结果带来一个向下的分量影响收敛精度,同时FG和FC也会加大最大功率点处的振荡问题。因此,本文提出自适应风力驱动优化算法(AWDO),将自适应权重加入FG和FC表达式,自适应权重为:
(14)
则,改进AWDO算法的速度更新为:
(15)
AWDO算法流程如图3所示。可知在寻优初期空气质点所受FG和FC都较大,寻优速度较快,可以快速搜索全局,而在寻优过程中随着空气质点不断接近最优结果自适应权重λ1和λ2值不断减小,空气质点所受FG和FC不断减小,更有利于寻优后期达到更好的精度,减小振荡幅值。

图3 AWDO算法流程
3 仿真结果和分析

图4 基于Boost电路光伏发电系统结构图
在标准温度下,即T=25 ℃时,在光照强度由1 000 W/m2突变到800 W/m2的情况下对P&O方法、WDO方法和AWDO方法进行仿真对比分析。基于Boost电路光伏发电系统结构如图4所示。表1为仿真模型参数。

表1 光伏发电系统仿真模型参数
光照强度将在1 s时发生突变,仿真的输出电压和功率如图5(a)和图6(a)所示。图5(b)和图6(b)、图6(c)和图6(c)为初始和突变时刻的放大图。可知,WDO法和AWDO法初始跟踪时间仅需P&O法的4.3%,且突变后的跟踪时间仅需P&O法的30%。同样情况下,WDO方法会使其输出电压向下偏离,输出功率也向下偏离。而AWDO法可以应对这种情况,且跟踪精度较高。同时,AWDO法的电压纹波为P&O法的20.13%,为WDO法的28.74%;AWDO法的功率纹波为P&O法的7.90%,为WDO法的3.66%。同样的AWDO法大幅减小了电压纹波和功率纹波,增强系统稳态。

图5 光照强度突变输出电压
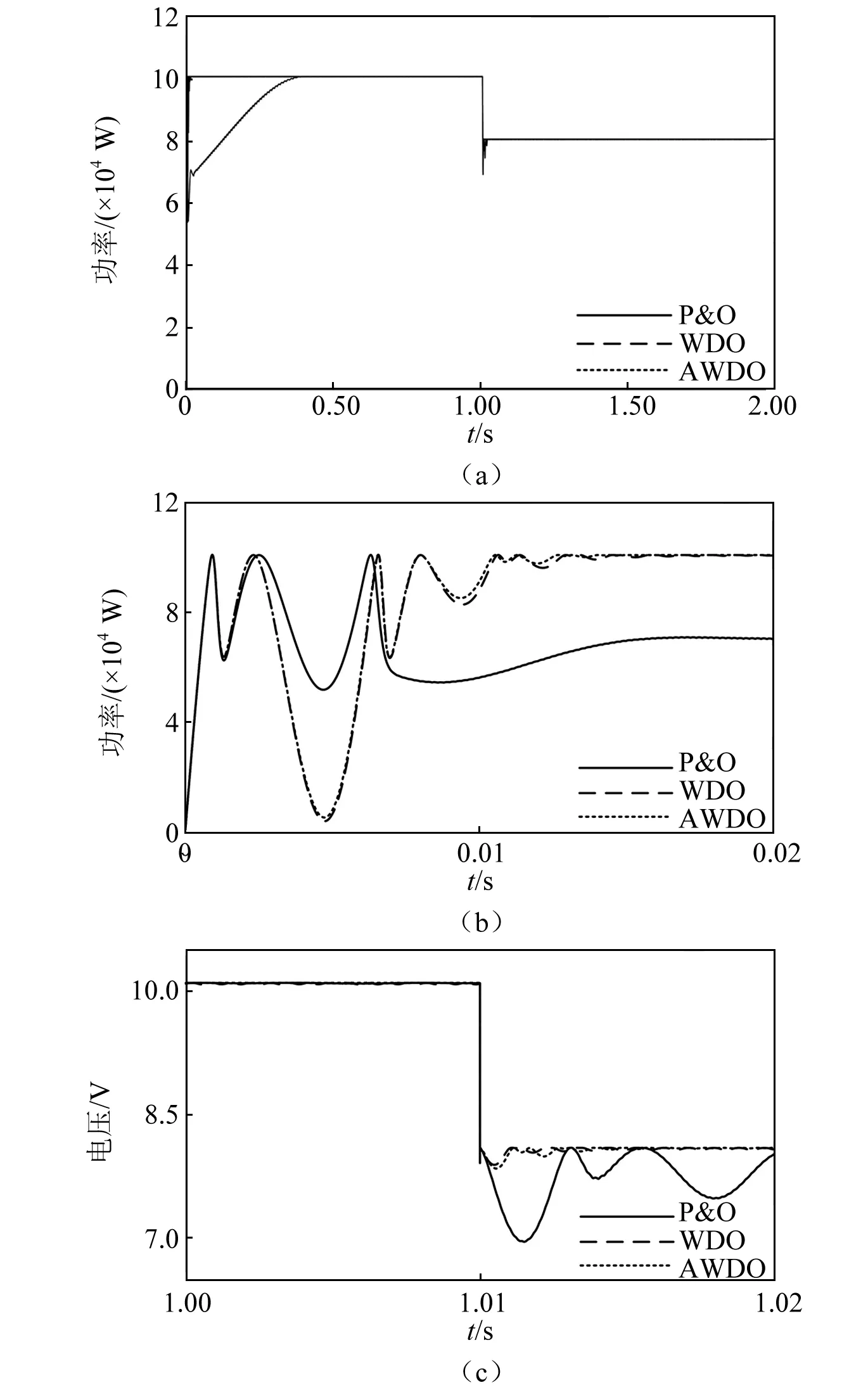
图6 光照强度突变输出功率
4 结束语
WDO是一种全局群体智能优化算法,具有实现简单、搜索效率高和收敛速度快等优点。本文提出了一种改进的自适应权值WDO算法,解决了重力和科里奥利力引起的负偏差问题。仿真结果表明,WDO算法和AWDO算法能够解决传统P&O方法无法兼顾跟踪速度和跟踪精度的问题。与WDO算法相比,AWDO算法明显改善了优化后期的振荡问题,有效保证了跟踪速度,提高了跟踪精度,具有良好的稳态响应。
