基于负载观测器的永磁同步电机模型预测控制

刘晨曦， 董学育， 朱建忠， 王健， 沈加政

(南京工程学院 电力工程学院，江苏 南京 211167)

0 引 言

永磁同步电机(permanent magnet synchronous motor, PMSM)因其功率密度大、运行高效、功率因数高而被广泛用于电梯牵引、电动汽车和航天智能等现代工业领域，其高效运行依赖于先进的控制策略。传统矢量控制法虽然易调整、易实现，但其电流响应速度慢、抗干扰能力差以及超调大，很难适应现代工业控制的发展[1]。

模型预测控制(model predictive current control, MPCC)在改善电机动态响应等方面有着广阔的应用前景，是目前国内外研究热点之一。其中控制变量是有限离散电流量的MPCC被称为有限集模型预测电流控制(finite control set model predictive current control, FCS-MPCC)。FCS-MPCC不需要调制单元，简化了电流内环设计，省去了复杂的参数调整，动态响应优越，并且容易实现非线性约束[2]。

为改善MPCC对电动机的控制性能，目前已开展较多研究工作。文献[3-4]利用无差拍和双矢量控制对电机的定子电流进行了预测，但没有考虑到外部负载干扰，电机的鲁棒性和稳定性差。文献[5]基于无差拍的电流预测控制，提出一种基于扰动观测器的方法来估计和补偿负载突变，但无差拍预测控制需要对运算单元进行调制，因此控制过程比较复杂，操作效率不高。

针对负载扰动对预测控制的影响，提出了一种基于永磁同步电机模型的电流预测控制策略，并在此基础上引入龙伯格(Luenberger)负载观测器，实现对转矩参考电流的前馈补偿。该方法可以有效改善负载干扰影响，从而使动态响应性能得到提高，系统鲁棒性得到加强。

1 PMSM的数学模型

假设磁路呈现非饱和状态，不考虑磁滞和涡流损耗等因素。基于此，永磁同步电机在同步旋转轴系下的电压方程[6]为：

(1)

式中：Ψd为d轴磁链，Ψd=Ldid+Ψf；Ψq为q轴磁链，Ψd=Lqiq；Ψf为转子永磁体磁链；Ld、Lq分别为d轴、q轴电感；ud、uq、id、iq分别为d轴、q轴电压和电流；ωe为转子电角速度；R为定子电阻。

电磁转矩方程为：

Te=1.5Pn(ψdiq-ψqid)

(2)

机械运动方程为：

(3)

式中：Te为电磁转矩；Pn为电机极对数；ωm为电机转子机械角速度；TL为负载转矩；B为电机黏滞摩擦因数。

2 有限集模型预测电流控制

本文以电流为控制对象，实现有限集模型预测电流控制。

2.1 预测模型

近似认为表贴式永磁同步电机有Ld=Lq=Ls。通过式(1)得到系统状态空间表达式，如式(4)所示。

(4)

在采样时间t足够小的前提下，利用一阶欧拉法[7]建立电流预测的离散模型。将电机d、q轴电压矢量u=[ud(k)uq(k)]T作为输入变量，d、q轴电流矢量i=[id(k)iq(k)]T作为输出变量和状态变量，并以离散状态空间函数的形式表达该预测模型。

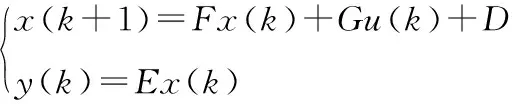
(5)

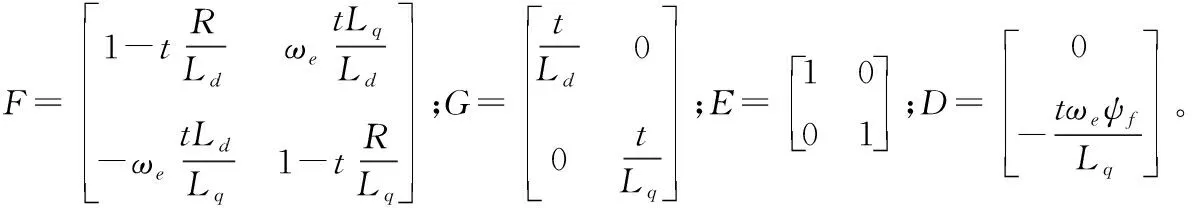
2.2 评价函数

电机控制系统通过逆变器输出控制电机运行,在建立预测模型后，为得出逆变器输入端的电压控制矢量，以上标“*”表示参考电流与预测电流之间的跟踪误差为控制项构造评价函数。

(6)

式(6)表明:评价函数g值越小，电机电流控制的跟踪性能越好。以上PMSM预测控制系统建模依赖于规定的数学模型，并未提及不可避免的外部负载扰动对控制性能的影响。

施药后，试验全程调查杂草5次，分别为药前调查基数，药后5天调查药剂防效药；10后天调查药剂防效；药后15天调查药剂防效；药后20天调查最终药剂防效，调查时小区对角线选取5点，每点（1m×1m）。目测试验药剂对水稻的安全性。

3 负载扰动观测器

为了消除负载扰动对控制系统的影响，采用基于电流环的预测控制方法，在系统转速环中加入龙伯格状态观测器[8]，以估计和补偿电机的转矩变量，增强系统抗扰性。

为了提高运算效率，本文将参考文献[8]的全阶龙伯格观测器设计降阶龙伯格观测器。利用观测到的电机转速误差作为反馈变量，在转速环对负载转矩进行校正。

(7)

构建龙伯格观测器状态空间表达式为：

(8)

若系统速度环按Tω周期采样，则通过离散化方程(7)，得出转速和负载观测值之间的递推关系式为：

(9)

图1 基于负载观测器的永磁同步电机有限集模型预测电流控制系统

4 系统仿真试验分析

4.1 试验条件设置

根据图1所示控制方案，采用id=0的控制策略，在MATLAB/Simulink环境下搭建基于负载观测器的模型预测电流控制仿真试验。电机模型采用Simulink/Simscape内置的模块。电机参数如表1所示。

表1 永磁同步电机参数

4.2 基于负载观测器的预测控制分析

为验证基于负载观测器的FCS-MPCC(简称MPCC+O)控制效果，将其与传统矢量控制(简称PI)以及不加观测器的FCS-MPCC(简称MPCC)进行对比分析。仿真条件为：电机以给定2 000 r/min阶跃转速空载启动，0.03 ms时突加额定负载10 N·m，并带载运行到0.06 s时将负载全部卸下，仿真时间设置为0.08 s；基于PI控制的速度环比例因数Kp=11，积分因数Ki=82，电流环比例因数Kp=4.23，积分因数Ki=500；基于预测电流控制的计算频率为10 kHz。首先按照试验条件，验证龙伯格观测器的估计值，如图2所示。

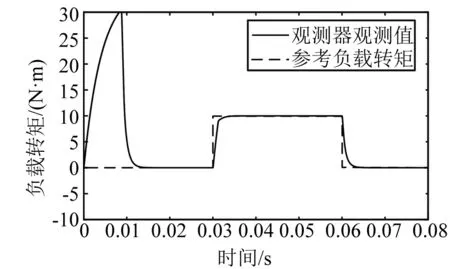
图2 龙伯格观测器的估计值

从图2可知，龙伯格观测器可以快速精确估计负载变动且无超调，说明观测器对实际负载扰动具有较好的跟踪特性，可以对负载突变进行准确估算和补偿。

图3 三种控制系统下的电机转速响应曲线

图3为三种控制系统下的电机转速响应曲线。在初始启动过程中，“PI”系统控制下电机转速的超调量和响应速度较慢。与常规“MPCC”系统相比，由于观测器对负载转矩电流的补偿作用，“MPCC+O”系统响应速度得到了提高，动态响应时间约为13 ms。与其他方法相比，该方法控制精度较高，响应速度较快，调整时间较短。在0.03 s和0.06 s引入10 N·m负载扰动时，“MPCC+O”系统输出的扰动补偿信号有效地抑制了负载突变引起的转速波动。与其他两系统相比，能更快恢复到参考转速，表明了扰动观测器的可行性。

图4 两种控制系统下定子相电流仿真曲线

图4为传统PI控制和基于负载观测器的电流预测控制系统下定子电流的变化曲线。与PI控制系统相电流波形相比，后者定子相电流具有更好的正弦性，再结合图2所反映的负载观测曲线，发现该系统下的定子电流随负载转矩波动实时变化，表明其具有良好的动态响应性能和稳态运行特性。

5 结束语

上述验证表明，

基于负载观测器的有限集模型预测电流控制系统适用于永磁同步电机的控制，在系统动态响应速度、稳态控制精度以及鲁棒性能等方面均优于传统矢量控制和常规模型预测控制。在转速跟踪、电流跟踪以及抗干扰性能等参数上都有较好的控制效果。由于模型预测控制的思路简单，适应性强，同时负载观测器可以实现对外部扰动及时的精确补偿，因此有广阔的应用前景。由于本文所述只对电机电流环应用预测控制，因此对包括速度环的电机整体控制系统研究也将是今后工作重点。