基于因子分析对大学数学公共课考试成绩的研究
2022-12-17顾海燕于芊竹蓝飞宏
顾海燕,于芊竹,蓝飞宏
(东北林业大学 理学院,哈尔滨 150040)
《概率论与数理统计》是各大高校普遍设置的一门公共基础课程,对培养学生的或然性思维的过程中占有重要作用,同时也是统计分析的一门基础课程,在数学、大数据、自动化等方面的研究作用显著,《概率论与数理统计》课程的开设旨在培养学生的应用数据分析的方法解决实际问题的能力,对培养学生数据分析具有核心作用,而该课程由于其自身的抽象性特点以及与确定性量化分析方法具有本质的区别,所以导致学生们往往在学习过程中产生较多的困难,使得最后的考试成绩参差不齐,难尽人意.从成绩的角度倒推学生们学习该门课程的影响因素,并在实际教学中加以适当处理,对于改善目前该门课程的教与学的活动无疑会有重要意义.
因子分析方法在对于成绩的分析过程中应用及其普遍,付政庆,郭兰兰,赵文才等人在职业教育培养中利用因子分析方法完成了各科成绩的评价并得到相关联的专业课程成绩彼此间的影响强弱[1];俞群俊,杨庆婷,李雅琳借助因子分析法研究了昆明医科大学2017级劳动与社会保障专业53名同学的18门课程期末考试成绩[2];廖羽祥,王海洋,王帅等采用因子分析对体育课平时成绩评价指标进行分层,确定了5个公共因子并对其命名释义,最终建立评价指标体系[3];黄嘉文,陈丹婷,温永仙利用因子分析对学生综合素质与能力进行客观评价的综合分析方法对具有相同学习特征的学生进行分组和聚类,得出本科学生存在各科类课程不均衡发展,缺乏创新实践能力等问题的结论[4];王小丽,曹雅妮,简太敏利用因子分析方法提取出五个影响学生成绩的潜在因子,并构建学生综合成绩的数学模型,在此基础上利用系统聚类分析法对学生成绩进行分类,客观地评价了各类学生的课程成绩,进而提出该校GIS专业建设的具体措施[5]; 雷玲,刘昭君结合疫情期间线上教学质量现存问题,以某高等院校为例,从四个层面设计了多个影响因素变量以及线上教学质量满意度变量,并利用障碍度诊断分析模型,实证分析了新冠肺炎疫情期间线上教学质量影响因素与障碍因子[6]; 目的分析预防医学专业学生课程成绩,综合评价不同学生的能力差异.许小琴,陈礼彬采用因子分析法和聚类分析法对福建医科大学2015级预防医学专业175名学生的47门课程成绩进行研究[7]; 武秋月在因子分析模型的基础上,提出了计算自驱力指数α的因子分析改进模型[8]; 钱芳斌,丁海洋提出了多维度、多阶段的在线开放课程效能评价指标和影响因素,并尝试构建了在线开放课程的效能评价体系模型,以保障在线开放课程的可持续性健康发展[9].由此可见,在高校课程成绩分析及教学质量的提升中,因子分析方法是一有力工具.
1 模型介绍
因子分析最早由英国心理学家C·E·斯皮尔曼提出,本质上是一种降维过程,而降维得到的公共因子称为“潜变量”,通常用于心理学、社会学和行为科学等领域的研究[10-12].用少数几个公共因子去描述许多指标或因素之间的联系,就可以相对运用较少的因子反应大部分的原数据所包含的信息.运用该项技术可以帮助我们应用于生活中的实际问题的分析.
1.1 因子模型
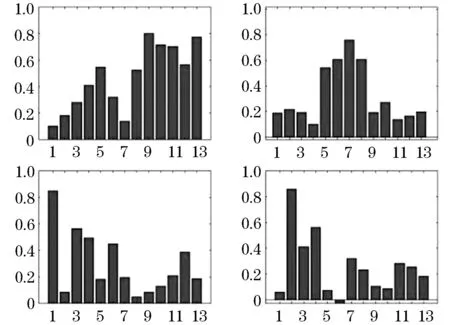
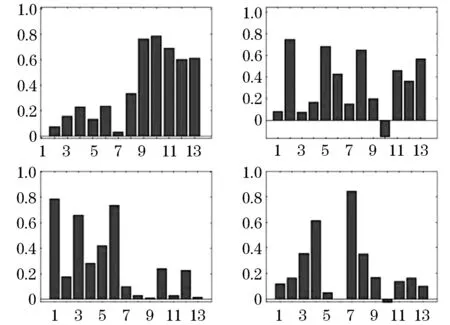
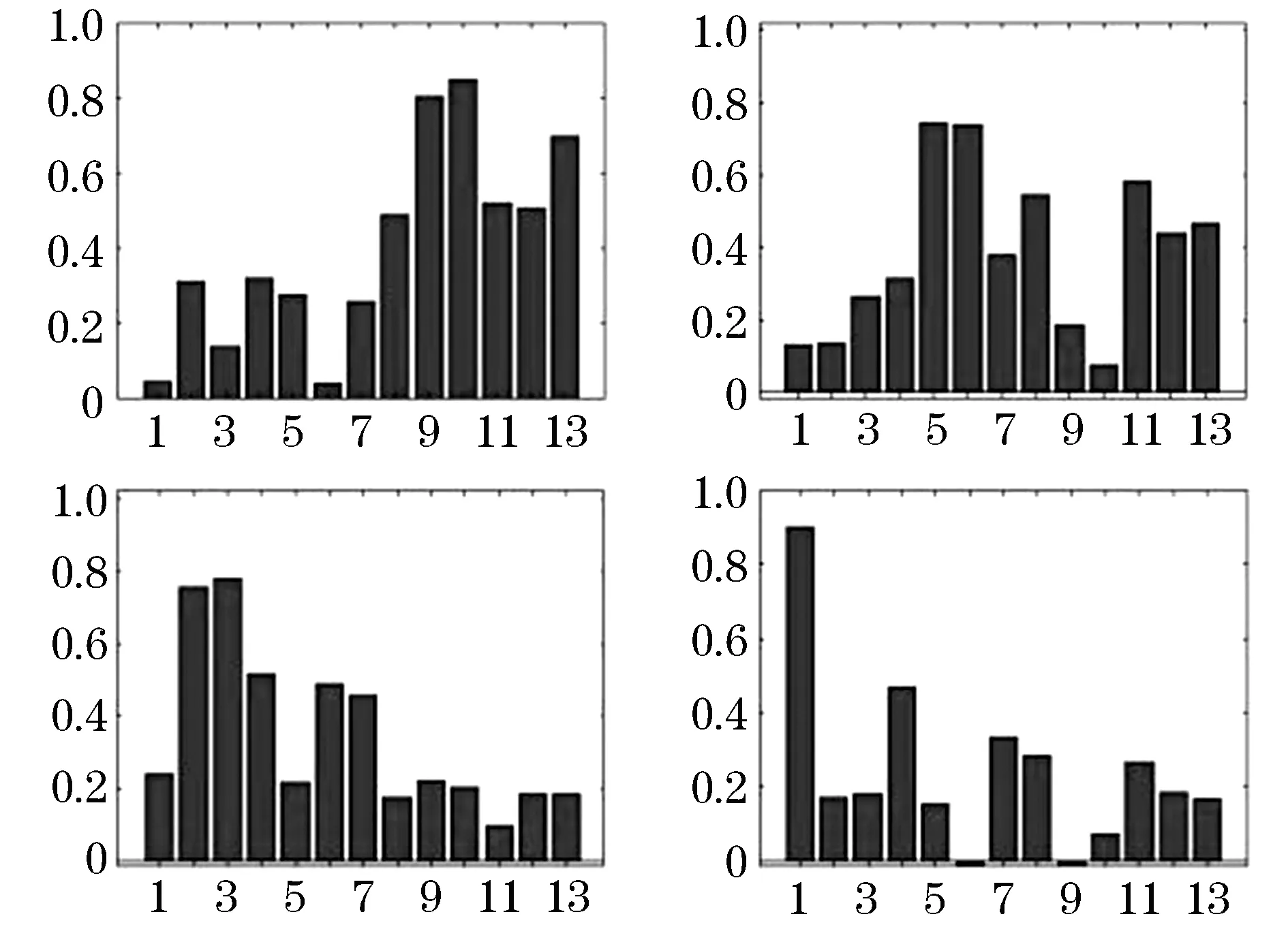
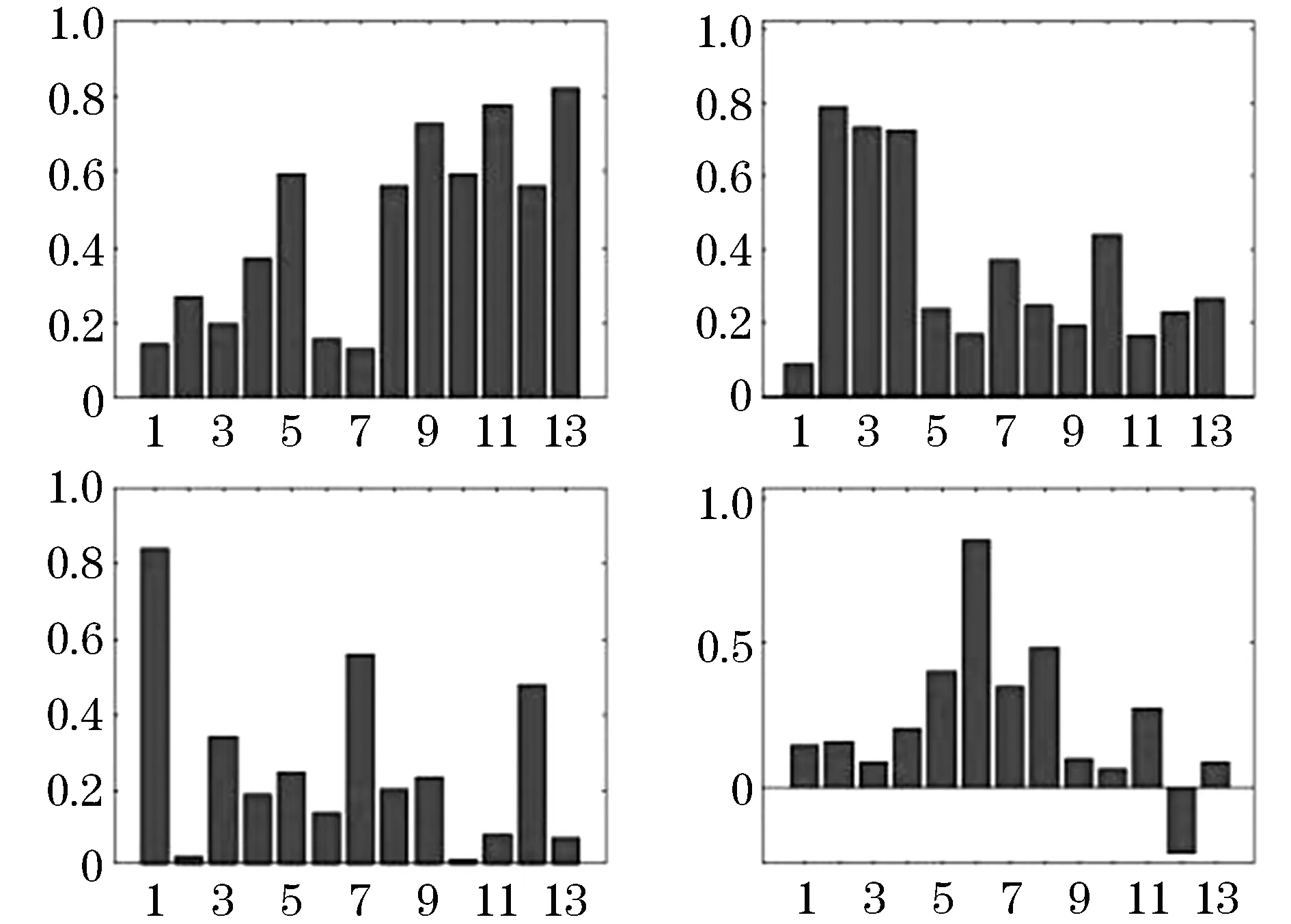
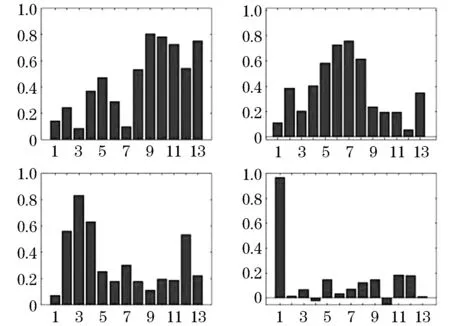
假设可观测随机向量y=[Y1,Y2,…,Yp]′的均值为μ,假定y线性依赖于m个不可观测的公共因子f=[F1…Fm]′和p个不可观测的特殊因子ε=[ε1…εp]′,通常m 其中:ljk为第j个变量在第k个因子上的载荷,体现了公共因子对此变量的解释能力[13].ljk表示公共因子对原始变量的解释能力,当因子载荷矩阵各列上的元素的绝对值越分散,说明该公共因子更易于解释. 因子分析的目的不仅是得到公共因子,更重要的是知道各个公共因子的实际意义,即突出各个公共因子的典型代表原始变量,为此可以对因子载荷矩阵施行正交旋转变换,使得因子载荷矩阵各列元素的平方两极分化,要么接近0,要么接近1,该方法称为最大方差正交旋转. 设T是一个正交矩阵,延用上面的因子载荷矩阵Lp×m,则最大方差正交旋转的因子载荷矩阵为[14] B=Lp×m×T. 有时需要把公共因子表示成原始变量的线性组合,或对每个样品计算公共因子的估计值,即因子得分.因子得分用于模型诊断,或进一步分析原始数据,比如排序、分类等.可表示为 Fi=si1y1+si2y2+…+sipyp,i=1,2,…,m 可以利用不同方法估计出sij的值,最后计算出Fi的值,称之为公共因子Fi的得分[15]. 本次分析数据来源某高校《概率论与数理统计》阶段一二和期末成绩.数据经过了简单处理,剔除了缺考学生成绩,包括阶段一4道主观题分数、阶段二4道主观题分数和期末5道主观题分数,去掉了选择题和填空题分数,公选用13道题的分数作为原始变量,样本容量为3 206人. 如表1所示,利用处理过的所有数据采用主成分分析法得到的KMO检验值为0.942,较大,巴特球度检验显著性水平小于0.001,结果说明这组数据适合进行因子分析. 表1 KMO检验和巴特利特球度检验结果 采用处理过的3 206个数据进行因子分析,选取了前4个公共因子,因为这4个公共因子有鲜明的实际意义,且反映原始变量的信息已占总信息的67%以上,虽然所占总信息的百分比不是那么高,但前4个公共因子已充分反映了学生答题的情况,对教师的后续教学已起到启示作用.见表2. 表2 公共因子贡献率及累积贡献率 由于利用主成分法得到的公共因子不利于解释,因此对因子载荷矩阵进行了最大方差因子旋转.见表3,第一个公共因子对t9~t13的载荷较大,t9~t13是期末试题的所有主观题,主要考察的知识点为:假设检验、区间估计、点估计、连续型二维随机变量等.第二个公共因子对t5~t8的载荷较大,t5~t8是阶段二试题的所有主观题,主要考察的知识点为:离散型二维随机变量、连续型二维随机变量、中心极限定理等.第三个公共因子对t2~t4的载荷较大,t2~t4是阶段一试题的除了第一道主观题的所有主观题,主要考察的知识为一维随机变量.第四个公共因子对t1的载荷要远远高于其他的原始变量,这道题考察全概率公式和贝叶斯公式. 表3 最大方差正交旋转后的因子载荷矩阵 将13道题利用四个因子的概括,实现了降维的效果,使其可以在低维度上对考试成绩进行研究,分析学生的知识掌握情况、逻辑思维能力、记忆能力等方面的信息.教师可以利用这些信息针对学生欠缺部分进行专门的训练,来达到提高教学质量的效果. 把处理过的数据按学院(分别为理学院、林学院、土木工程学院、经济管理学院、交通学院、工程技术学院、信息与计算机科学学院、机电工程学院)分成8组数据,对这8组数据分别建立因子模型. 图1~8为8个学院的可视化因子载荷图,这8个学院的因子模型均选取前4个公共因子,横坐标表示题目标号,表示公共因子对各道题的因子载荷. 从图1~8可以看出,各个学院的因子模型的第一个公共因子都是对期末试题的载荷较大,其中t9、t10的因子载荷明显比其他的变量要大,不分学院的因子模型的第一个公共因子反映的信息是一致的.工程技术学院、经济管理学院、林学院、信息与计算机科学学院的因子模型的第二个公共因子对t5~t8的载荷较大,与不分学院的因子模型的第二个公共因子反映的信息是一致的,但是其他学院的因子模型的第二个公共因子没有反映此信息,如对于机电工程学院和土木工程学院,第二个公共因子主要解释原始变量t2和t3,由此可见不同学院的学生对本课程的掌握具有明显的差异性,因此教师应该结合学院专业不同调整上课进度、方式、着重哪些的知识点讲解等.第三个公共因子只对交通学院的试题t7和t9分数有负向的影响,说明第三个公共因子得分越低学生成绩越高.8个学院的因子模型的第四个公共因子出现了负数的载荷,且多数学院的因子模型的第四个公共因子对t1的因子载荷很大,这与部分学院的因子模型一致. 工程技术学院、机电工程学院和信息与计算机科学学院的因子模型的前四个公共因子对原始变量的解释较为相似,可见这三个学院对本课程的学习有一定的共通性,这3个学院都是工科学院,因此学生逻辑思维能力较强,体现了工科学生的特点. 图1 可视化因子载荷(工程技术学院) 图2 可视化因子载荷(机电工程学院) 图3 可视化因子载荷(交通学院) 图4 可视化因子载荷(经济管理学院) 图5 可视化因子载荷(理学院) 图6 可视化因子载荷(林学院) 图7 可视化因子载荷(土木工程学院) 图8 可视化因子载荷(信息与计算及工程学院) 针对全校本课程的各道主观题分值建立的因子模型,用前4个公共因子反映出学生学习本课程的各方面能力,以此调整教学方法. 针对8个学院学生的本课程的各道主观题分值建立的8个因子模型,也选取前4个公共因子,不同学院表现出不同的结果,因此提示教师在教学中应该结合专业进行讲解.1.2 最大方差的正交旋转
1.3 因子得分
2 模型建立
2.1 数据来源及数据处理

2.2 不分学院的因子模型

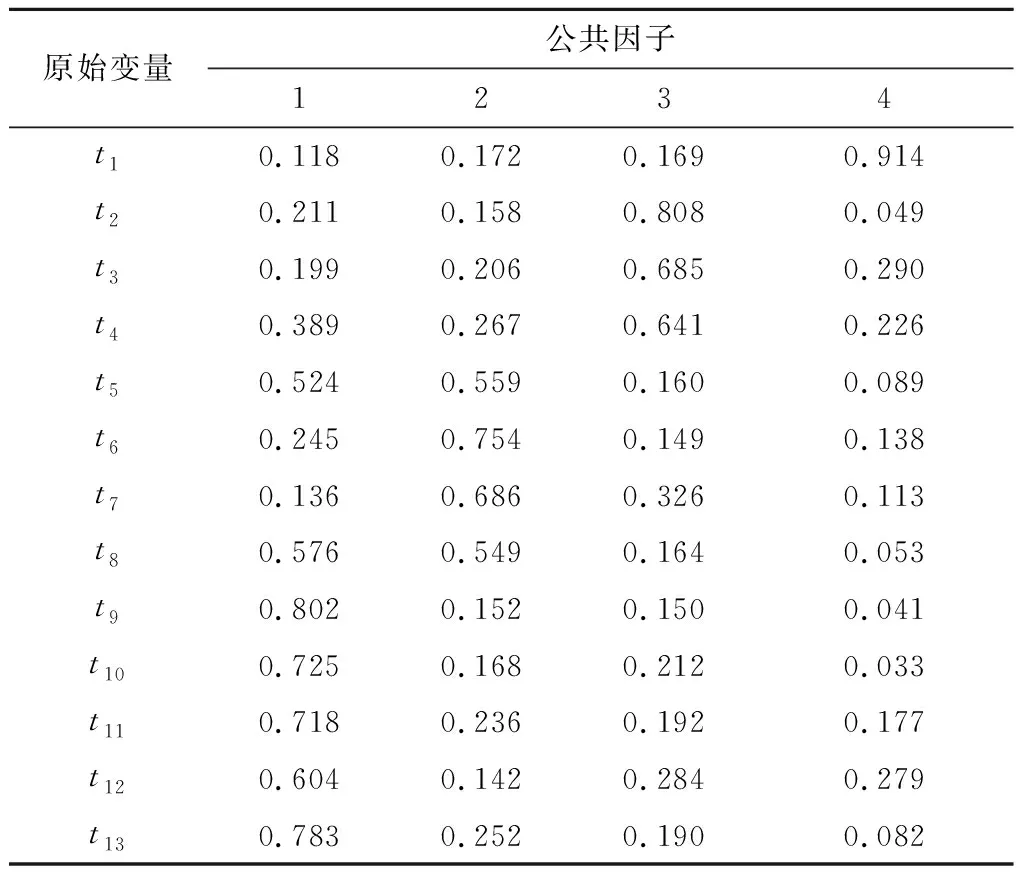
2.3 各个学院的因子模型
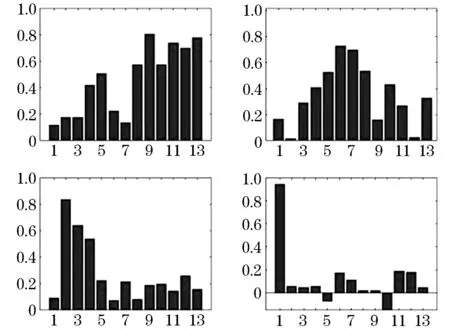
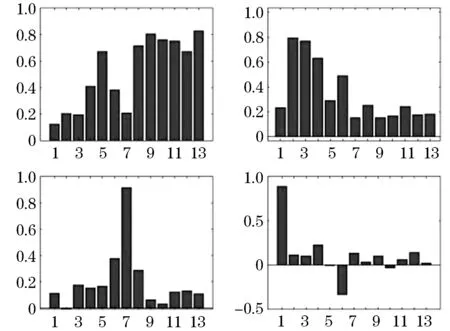
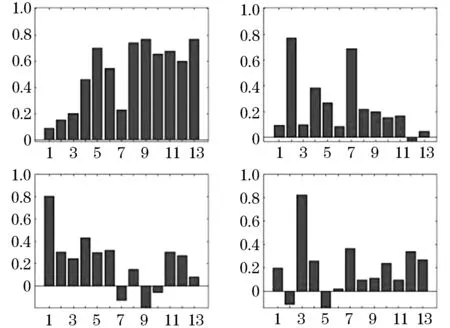
3 结 语
