钢纤维增强高性能混凝土弯曲疲劳寿命预测研究

李 晨,陈思可,方兆麟

1. 广东粤海珠三角供水有限公司，广州 511455；2.广东省水利水电科学研究院，广州 510635；3.广东省水利新材料与结构工程技术研究中心，广州 510635；4. 广州市花都区灌区管理中心，广州 510800)

1 概述

钢纤维增强高性能混凝土(Fiber Reinforced High-performance Concrete，FRHPC)是一种具有高强度、高韧性和优异耐久性的水泥基复合材料[1-2]。近年来，FRHPC因其突出的力学性能和耐久性，逐渐应用于道路、建筑、核电、海洋和军事等工程领域[3]。同时，FRHPC工程应用节能减排效果显著，贴合“绿水青山就是金山银山”理念，符合社会可持续性发展要求，蕴含巨大工程应用价值。FRHPC为主体的建筑结构在服役过程中常受到循环荷载作用(如车辆、行人、地震等)的影响，产生疲劳损伤。随着服役周期的增长，FRHPC疲劳损伤逐渐累积，导致其力学性能和耐久性降低，甚至影响建筑结构安全性和可靠性[4]。因此，开展FRHPC疲劳损伤研究具有重要的工程意义。

目前，对混凝土疲劳性能的研究，集中利用经验公式(见表1所示)[5-6]，建立应力水平(S)和疲劳寿命之间的关系，预测混凝土在服役过程的疲劳寿命。Wholer建立了单对数疲劳方程，研究纤维掺量对普通混凝土疲劳寿命的影响，其中A=1.436和B=-0.105，并提出疲劳极限强度位于0.55-0.65之间[7-8]。文献[9]引入应力比R(=fmin/fmax)，模拟了实际结构工程中最小循环荷载不等于零的实际加载情况；文献[10]探讨了不同应力水平下纤维增强混凝土疲劳寿命，并对Wholer提出的单对数方程进行改进，引入材料系数β，定量预测纤维增强混凝土的疲劳寿命；文献[11]通过FRC弯曲疲劳试验，建立了存活率P=50%时的双对数疲劳曲线方程，A=0.339，B=0.138，得到了用于工程实际中不同存活率的S-N曲线方程。文献[12]考虑混凝土结构疲劳寿命的离散型，所以在S-N曲线中引入失效概率Pf表征疲劳寿命的离散型，预测了纤维增强混凝土疲劳寿命(见表1)。

表1 混凝土疲劳经验公式总结

由上述可知，应力水平S与疲劳寿命N之间的关系可以通过不同的经验公式和误差分析方法表征。目前，多数经验公式集中于建立应力水平(S)和疲劳寿命(N)数学关系式，然而疲劳寿命影响因素众多，即使在试验条件完全相同的情况下，试件的疲劳寿命也存在着很大的离散性，想要在实际应用中用结构材料的物理量定量的分析疲劳寿命具有一定难度。为了正确反映在不同纤维掺量下FRHPC疲劳寿命的变化规律，运用概率理论对混凝土疲劳寿命与可靠性进行宏观分析和估计就显示出逻辑上、理论上和实质上的必要性和合理性。

因此，本研究针对FRHPC疲劳寿命的分散性，采用Weibull分布函数对其分布规律进行表征；通过图像法、矩量法和极大似然估计法定量评价了威布尔分数函数中形状参数α和特征疲劳寿命u，并结合Kolmogorov-Smirnov验证Weibull函数的可靠性；在此基础上，建立了FRHPC疲劳寿命方程，确定方程中参数，量化应力水平S和疲劳寿命N的关系，进一步引入失效概率Pf，建立具有一定存活率的Pf-S-N方程。

2 原材料与试验方法

2.1 原材料

试验采用珠江水泥厂生产的PII 42.5硅酸盐水泥，山东盈润智能新材料有限公司生产的平均粒径为0.2 μm硅灰和一级粉煤灰，河源万川公司生产的粒径范围为0.9 mm～2 mm的石英砂和5 mm～20 mm连续级配碎石；减水剂为广东瑞安高性能混凝土用Ls-PC(A)型减水剂，固含量为33.0%。钢纤维采用赣州大业金属纤维有限公司生产的WSF0206(B)型钢纤维，长度为13 mm，直径均为0.2 mm，抗拉强度为2 850 MPa。FRHPC配合比为水泥：硅灰∶粉煤灰∶细骨料∶粗骨料∶水=460∶100∶40∶626∶1 021∶168，钢纤维占总体材料的体积分数掺量为0.5%，1.0%，1.5%。

2.2 试验方法

FRHPC弯曲疲劳试验在MTS Landmark 370.25 动态疲劳试验机上进行。MTS高性能动态疲劳测试系统为250 kN全数字轴向电液伺服测试系统，集成MTS伺服液压、多功能FlexTest控制器和成熟可靠的MTS应用软件和全套附件，可为混凝土提供高精度、良好重复性的动静态测试。MTS测试系统自动采集疲劳循环次数、荷载变化过程及峰值荷载等基本参数。

FRHPC疲劳寿命样本容量确定为8个。为了消除试样受力面不平整而造成的试验误差，在试样上表面受压部位，涂抹上一层高强石膏，然后对FRHPC梁进行预加载(0.5 kN)，反复几次，确保高强石膏压实，并与疲劳试验机加载点完全接触。

FRHPC采用力控制模式。疲劳荷载历程先以10 kN/min的加载速率至平均荷载(最大应力值σmax和最小应力值σmin的平均值)，然后以正弦波的形式等幅值加载(最大应力值σmax和最小应力值σmin保持不变)，加载频率为8 Hz(常用加载频率为5～15 Hz)。循环特征值r(最小应力值σmin和最大应力值σmax的比值，r=σmin/σmax)取0.1，应力水平S(最大应力幅值σmax和静载抗折强度fr的比值，S=σmax/fr)取0.65、0.70、0.75和0.80。

3 试验结果与讨论

3.1 疲劳试验结果

为了确定循环荷载应力水平，需要首先评价FRHPC抗折强度，随着纤维掺量的增加，FRHPC抗折强度随着增大。当纤维体积掺量Vf=0.0%时，FRHPC基体抗折强度为5.8 MPa，当纤维体积掺量为0.5%、1.0%、1.5%和2.0%时，其抗折强度分别提高了44.20%、85.68%、99.21%。

不同应力水平(S=fmax/fr；fmax=最大疲劳应力；fr=静态弯曲强度)作用下，掺入不同体积掺量(Vf=0.5%、1.0%和1.5%)钢纤维的FRHPC疲劳寿命如表2～表4所示。从表2～表4可以看出，相同应力水平作用下，随着纤维体积掺量的增加，FRHPC的疲劳寿命逐渐增大；纤维掺量相同时，随着应力水平降低，FRHPC疲劳寿命逐渐增大。如应力水平S=0.65时，FRHPC疲劳寿命随着纤维掺量的增加，最大疲劳寿命由282 145次增大到1 020 000次；当纤维体积掺量为0.5%时，随着应力水平的减小，最大疲劳循环次数由344增加到282 145次。文献[13]研究了钢纤维增强混凝土(Steel Fiber Reinforced Concrete，SFRC)弯曲疲劳性能，同样发现SFRC的疲劳寿命随着纤维掺量的增加而增大。

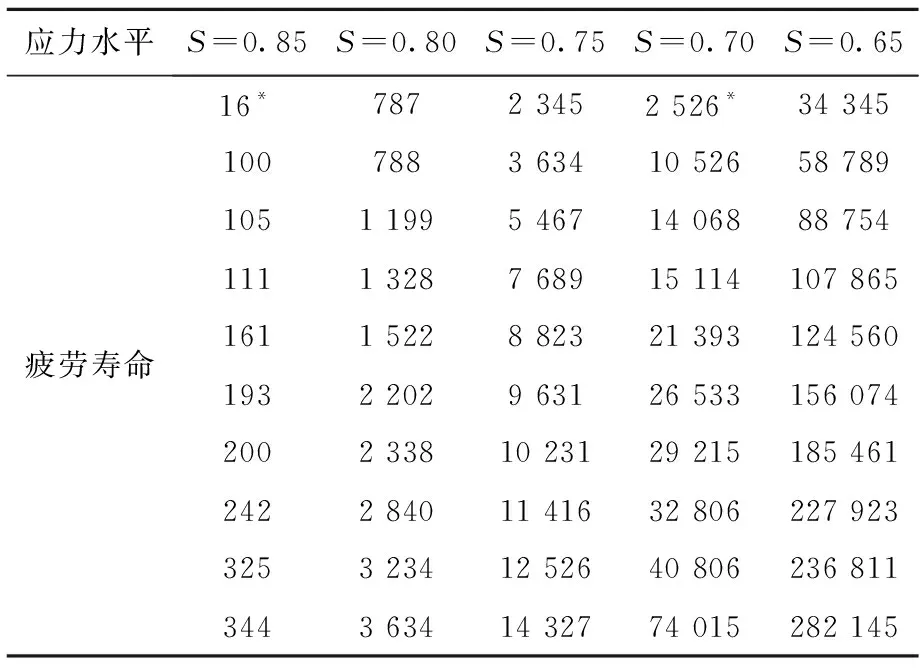
表2 FRHPC疲劳寿命(Vf=0.5%)

应力水平S=0.85S=0.80S=0.75S=0.70S=0.65疲劳寿命40*1 75114 84325 57835 3591431 86915 16030 42676 2182262 91718 64544 672108 2362473 40425 18455 622144 4962704 40626 40076 218189 7823245 67933 52791 246207 4364266 94142 345105 376242 4965377 65451 640134 984289 2126818 91261 616179 240365 78983410 24576 117207 856420 385

表4 FRHPC疲劳寿命(Vf=1.5%)

3.2 疲劳寿命分析

3.2.1威布尔函数分布

由于混凝土结构内部缺陷的不确定性和纤维分布的不均匀性导致FRHPC疲劳寿命分散性较大，所以研究者提出各种数学概率模型用于统计分析混凝土疲劳寿命分布情况。目前，常用于分析混凝土疲劳寿命分布的数学概率统计模型为威布尔分布函数(Weibull distribution)。

威布尔概率分布函数f(n)和累积分布函数Pf(n)如下式所示：

(1)

(2)

n≥no,s>0；α>0；且u≥no,s。

式中：

n——随机变量N的具体数值；

α——特定应力水平S作用下，威布尔分布的形状参数；

u——疲劳寿命的特征值；

no,s——位置参数或疲劳寿命的最小值。

根据等式(2)可以得到疲劳寿命的生存函数即可靠性函数LR(n)：

(3)

对于SFRC而言，文献[14]认为可以假设威布尔分布函数在实际应用中其最小疲劳寿命no,s=0，则可靠性函数LR(n)可以简化为两参数威布尔函数分布：

(4)

等式(4)两边取2次对数可得：

(5)

图1利用图像法对不同应力水平作用下FRHPC的疲劳寿命进行线性回归分析。由图1可知：两对数疲劳寿命基本呈线性分布，其最小相关系数为90.74%，即FRHPC的疲劳寿命符合威布尔参数分布。

Vf=0.5%

Vf=1.0%

Vf=1.5%图1 图像法分析分析FRHPC疲劳寿命示

3.2.2威布尔分布函数参数

利用图像法不仅可以判断FRHPC的疲劳寿命是否符合威布尔分布函数，而且可以根据线性回归分析得到形状参数α和特征疲劳寿命u。

利用矩量法评估威布尔函数分布参数需要适当的样本矩,威布尔函数分布的样本矩可用下式表达[13]：

(6)

式中：

T(x)——伽马函数；

E(n)——平均期望值。

极大释然估计法在迭代过程中，以图像法或矩量法得到的形状参数α作为第一个估计值，然后逐步迭代出极大似然估计值α*；把形状参数的极大似然估计值α*代入等式估计等式，可以计算得到θ*：

(7)

(8)

其中:α*和θ*分别为α、θ的极大似然估计值。

利用图像法、矩量法和极大似然估计法所求FRHPC威布尔函数参数见表5～表7中。

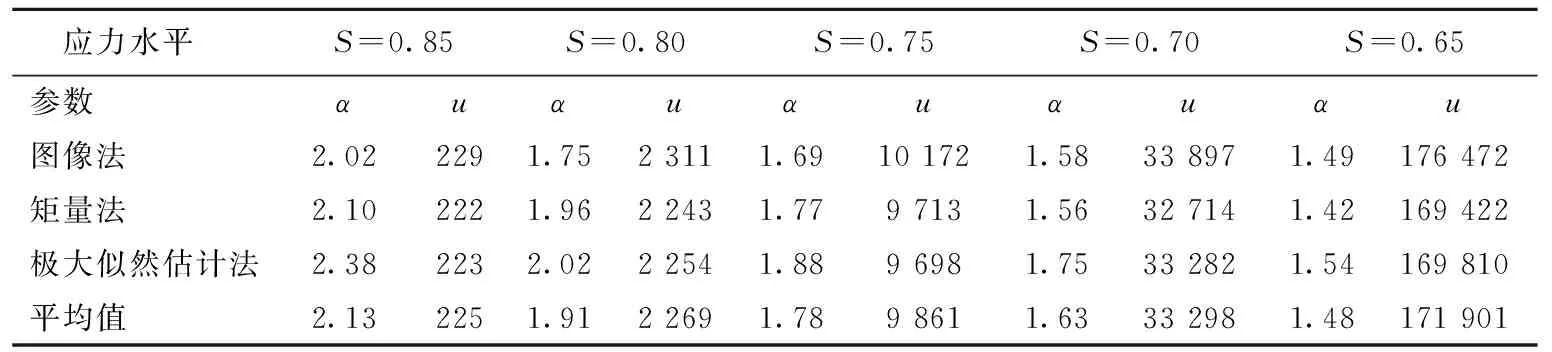
表5 FRHPC的疲劳寿命威布尔函数分布参数(Vf=0.5%)

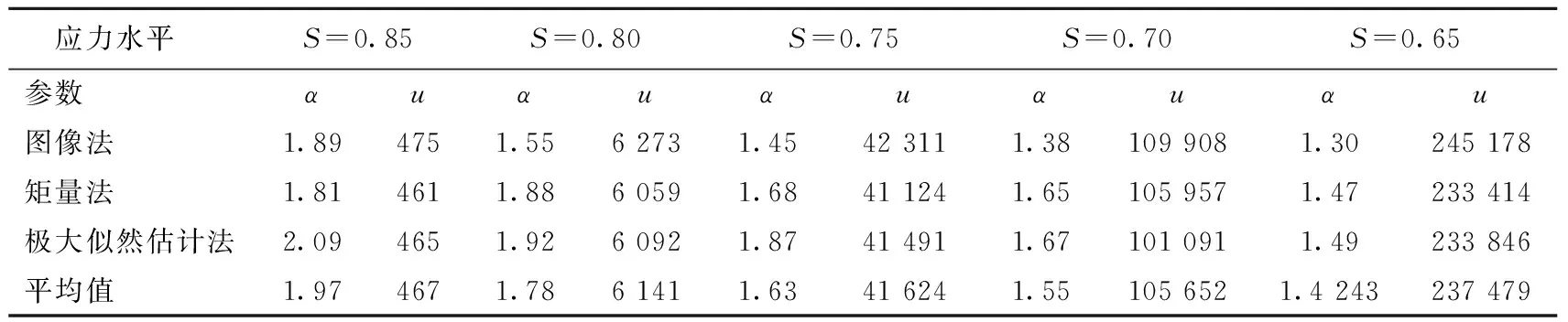
表6 FRHPC的疲劳寿命威布尔函数分布参数(Vf=1.0%)

表7 FRHPC的疲劳寿命威布尔函数分布参数(Vf=1.5%)

从表5～表7中可以看出，纤维体积掺量相同时，形状参数α随着应力水平的减小而降低。对于表中的形状参数而言，当应力水平较高时，形状参数α减小的幅度较大；当应力水平较低时，形状参数α减小的幅度降低。由此可以推断出，高应力水平作用下，FRHPC疲劳寿命的分散性较小；低应力水平作用下，FRHPC疲劳寿命的离散型较大。纤维掺量相同时，随着应力水平的降低，FRHPC特征疲劳寿命增加；当应力水平相同时，随着纤维掺量的增加，FRHPC特征疲劳寿命增加。

3.2.3引入失效概率Pf表征S-N关系

早期有关SFRC的S-N关系的研究，并没有引入失效概率Pf的概念。威布尔分布函数被用于表征SFRC疲劳寿命以后，开始用于计算不同应力水平下SFRC疲劳寿命的失效概率Pf。首先，不同应力水平下的疲劳寿命由大到小依次排列。然后，利用计算不同应力水平下FRHPC疲劳寿命所对应的失效概率。根据上述步骤，绘制出失效概率Pf和FRHPC疲劳寿命关系图(Pf-N)；然后计算失效概率Pf所对应的不同应力水平作用下FRHPC的疲劳寿命(S-N)；最后，在S-N回归直线的基础上，计算疲劳寿命相同时，不同应力水平S对应的失效概率Pf的数值(S-Pf)。图2～图4为一定失效概率下不同应力水平下FRHPC疲劳寿命分布的S-N-Pf曲线族。

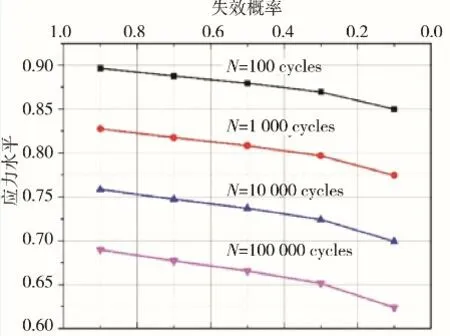
图2 弯曲荷载作用下FRHPC的S-N-Pf示意(Vf=0.5%)

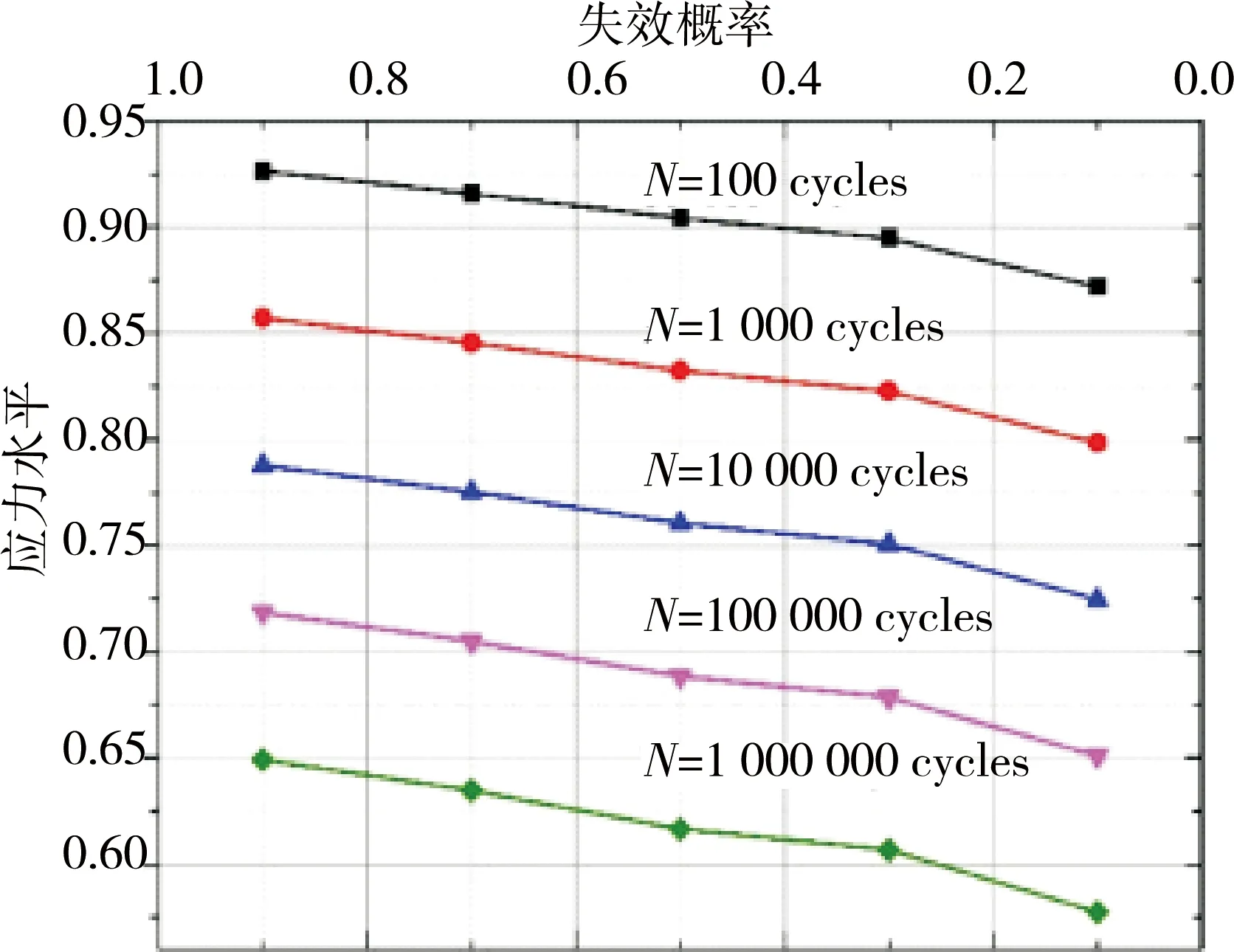
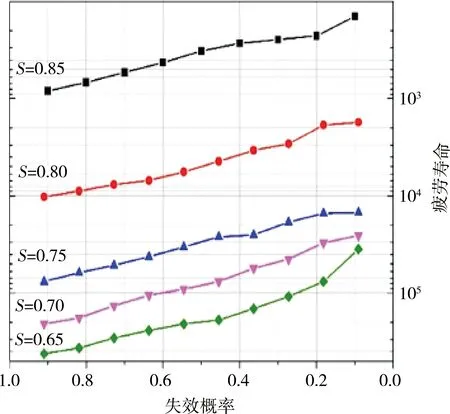
图3 弯曲荷载作用下FRHPC的S-N-Pf示意(Vf=1.0%)

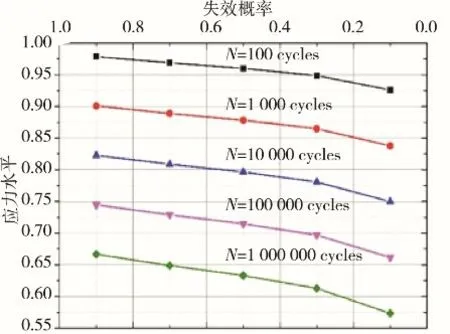
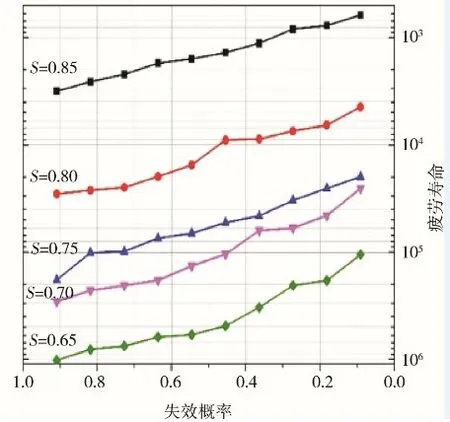
图4 弯曲荷载作用下FRHPC的S-N-Pf示意(Vf=1.5%)

(9)

(10)

上述分析一定失效概率下不同应力水平下FRHPC疲劳寿命分布的S-N-Pf曲线族。但是，并没有给出定量预测不同失效概率下FRHPC的定量评价公式。

另一种描述S-N-Pf关系的方法是基于文献[14]提出的数学等式：

L=(1-Pf)=(10)-a(S)b(logN)c

(11)

式中：

a、b、c——试验常数；

S——应力水平；

L——生存概率函数，L=1-Pf，其中Pf为失效概率。

式(1)为生存概率函数L、应力水平和疲劳寿命的关系式。为了准确表征S-N-Pf的数学关系，首先根据FRHPC的疲劳寿命计算出试验常数a，b和c的值。

等式(11)两边取2次对数：

log(-logL)=log(a)+blog(S)+clog(logN)

(12)

上述等式可以简化为：

Y=A+bX+cZ

(13)

其中，Y=log(-logL)；A=log(a)；X=log(S)；Z=log(logN)。为确定特定应力水平S下，具有一定生存概率L的FRHPC疲劳寿命N，式(13)变换为：

Z=A′+B′X+C′Y

(14)

式中，A′=-A/c；B′=-b/c；C′=-1/c。

基于样本均值中计算试验常数的便捷性，上述表达式可以转化为：

∑Z=∑A′+B′∑X+C′∑Y

(15)

(16)

(17)

等式(17)减去等式(15)可得：

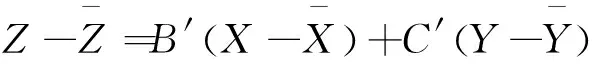
(18)

或者：

z=b′x+c′y

(19)

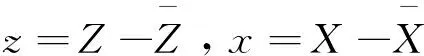
根据FRHPC疲劳寿命试验数据，可以统计计算∑x2、∑y2、∑z2、∑xy、∑xz和∑yz的值(见表8)。

表8 根据不同纤维掺量FRHPC的疲劳寿命统计参数

利用最小二乘法，可以得到以下方程：

b′∑x2+c′∑xy=∑xz

(20)

b′∑xy+c′∑y2=∑yz

(21)

将表8中的统计数据代入等式(20)和(21)可以得到系数b′和c′的值。纤维体积掺量不同的FRHPC的S-N-Pf关系表达式为：

FRHPC(Vf=0.5%)：

L=(10)-1.768 8(S)34.608 2(logN)12.187 7

(22)

FRHPC(Vf=1.0%)：

L=(10)-2.035 29(S)73.526 5(logN)29.411 7

(23)

FRHPC(Vf=1.5%)：

L=(10)-2.692 8(S)30.259 1(logN)15.060 2

(24)

4 结语

1) 相同应力水平作用下，随着纤维体积掺量的增加，FRHPC的疲劳寿命逐渐增大；纤维掺量相同时，随着应力水平降低，FRHPC疲劳寿命逐渐增大。

2) 两对数疲劳寿命基本呈线性分布，其最小相关系数为90.74%，即FRHPC的疲劳寿命符合威布尔参数分布。高应力水平作用下，FRHPC疲劳寿命的分散性较小；低应力水平作用下，FRHPC疲劳寿命的离散型较大。

3) 一定失效概率下不同应力水平下FRHPC疲劳寿命分布的S-N曲线可用下列等式计算：FRHPC(Vf=0.5%):L=(10)-1.768 8(S)34.608 2(logN)12.187 7、 FRHPC(Vf=1.0%)：L=(10)-2.035 29(S)73.526 5(logN)29.411 7、FRHPC(Vf=1.5%)：L=(10)-2.692 8(S)30.259 1(logN)15.060 2。