面向复杂条件的北斗/GNSS数据粗差处理方法
2022-12-16李雪珍章浙涛刘欢袁海军
李雪珍 章浙涛 刘欢 袁海军
0 引言
全球导航卫星系统(GNSS)包括全球的、区域的卫星导航系统以及增强系统,如美国的全球定位系统(GPS)、中国的北斗卫星导航系统(BDS)、俄罗斯的全球卫星导航系统(GLONASS)、欧洲的伽利略卫星定位系统(Galileo)、日本的准天顶系统(QZSS)等.GNSS在全球或区域范围内提供定位、导航和授时(PNT)服务,被广泛应用于自然灾害监测、变形监测、航空运输、防震减灾、车辆驾驶等领域.BDS是中国自主研发、独立运行的卫星导航系统,其发展分为3个阶段:北斗卫星导航试验系统(BDS-1)、区域北斗系统(BDS-2)和全球北斗系统(BDS-3)[1-2].如今BDS-3已经建成,由3颗地球静止轨道(GEO)卫星、3颗倾斜地球同步轨道(IGSO)卫星和24颗中圆地球轨道(MEO)卫星组成,于2020年向全球用户提供导航定位服务[3].BDS-3在继承BDS-2原有B1I和B3I信号的同时,新增了B1C、B2a和B2b频点[4].目前BDS能接收更多的可见卫星信号,得到更优的有效观测数据,实现良好的卫星几何构型,进而提升定位精度.BDS全球服务水平和高程定位精度达到10 m,在亚太地区可达到5 m,系统服务可用性优于95%[5].
GNSS实际应用环境是复杂且恶劣的.在城市峡谷环境中,高大建筑物的表面及街道上的树木和车辆等物体使卫星信号产生一定的反射和折射现象[6].卫星信号的衰减、中断导致可见卫星数量的减少和卫星几何分布不理想,出现较多较为严重的粗差.少量的粗差,能对参数估计的结果造成干扰,进而严重影响GNSS定位的精度和可靠性.目前用户对于定位的实时性、精度、可靠性的需求急速增加.在多频多系统和城市峡谷环境等复杂条件下,如何有效抵御粗差的影响是GNSS数据处理中的棘手问题,更是数据质量控制的关键点.为剔除粗差,提高定位精度,北斗/GNSS数据的粗差处理主要可概括为两大类方法:基于均值漂移的粗差处理方法[7-8]和基于方差膨胀的粗差处理方法[9].
本文以最常用的数据探测及稳健估计为例阐述两类粗差处理方法的流程,并研究给出了适用于复杂条件的阈值方案,最后利用实测数据的GPS+BDS组合定位进行验证.
1 基于均值漂移的粗差处理
GNSS函数模型中的粗差通常会导致最小二乘估计存在偏差.基于均值漂移的粗差处理即粗差纳入函数模型,认为含有粗差的观测值,其期望发生平移[10].最早提出且目前使用最为广泛的基于均值漂移的粗差处理方法是数据探测(data snooping)[7].
具体而言,数据探测依赖于在原假设模型和一组备选假设模型之间进行假设检验,要求检验统计量必须遵循正态分布、τ分布、x2分布和F分布[11-12].此外,由于观测模型的几何形状[11]、假设之间的可分离性[13]、选择的统计量[14]、预先确定的临界值[15]等原因,不可避免地会产生漏检、误报和错误识别,因此并不能完全消除偏差并确保最终参数估计的无偏性.数据探测最初只是针对一个粗差研究的.在复杂条件下,一组观测值包含多个粗差时,数据探测只能一个接一个地探测,难以满足实际的应用需求.而多维粗差的同时定位与定值(ELGE法)不仅能确定多个粗差的位置,还能求出各个粗差的数值大小[16].部分最小二乘平差把观测值是否含有粗差分成两组,在不含粗差的一组里实施最小二乘平差,同样能求出多个粗差的位置与数值[17].与上述以残差为对象的方法不同的是拟准检定法,它依据观测值的真误差判断粗差的位置[18].在观测值相互独立且等权时,以上几种方法可以认为是等价的[19-20].
Baarda[7]最早提出测量系统的可靠性理论.可靠性分析为粗差探测提供了相应的理论基础.可靠性分析的3项重要指标分别是最小可检测偏差(MDB)、内部可靠性和外部可靠性[21].其中MDB指在一定正确检验概率条件下可被检测到的最小偏差的绝对值.内部可靠性指的是发现粗差的能力,外部可靠性是指不可发现粗差对平差结果的影响程度[22].对于多个备选假设的情况,最小可分离偏差(MSB)和最小可识别偏差(MIB)被研究和定义,它们可衡量与另一个备选假设成功分离或在多个备选假设中以一定的概率正确识别的最小偏差的大小[13,23].将MDB代入参数解得到外部可靠性,以衡量未检测到的粗差对估计结果的影响显著性.其他相关的可靠性测量也被研究,如可靠性数据指标[24]和可控性(区域三角)[25].目前,基于均值漂移的粗差处理方法已被广泛应用于各种领域,如大地测量网的质量控制和完好性监测等.
2 基于方差膨胀的粗差处理
另一类基于方差膨胀的粗差处理方法认为含有粗差的观测值的方差发生变化,但期望不变[5].基于方差膨胀的粗差处理方法的研究主要集中在稳健估计(抗差估计)[22,26].稳健估计将粗差纳入随机模型,通过逐次迭代平差结果,不断改变观测值的权,最终使含有粗差的观测值权为零.稳健估计主要依赖等价权函数来检测和排除GNSS观测数据中的粗差[27].稳健估计主要包括M估计(广义极大似然估计)[28]、R估计(秩检验估计)[29]、L1范数估计[30]、最小截平方和估计[31]、符号约束的稳健估计[23].M估计的抗差性和有效性主要取决于所采用的参数的可靠性、等价权函数及其临界值的合理性[32],因此不同权函数消除或减弱粗差影响的能力不尽相同.已有许多不同的权函数能高效和准确处理独立观测值和相关观测值,如双重法[33]、Huber法[27]、Hampel法[34]、Danish法[35]、IGGI法[36]和IGGIII法[9,37].其中IGGI作为国内早期经典的质量控制算法,它依据残差的假设检验结果调整权阵来减弱含粗差的观测值对定位的影响.在IGGI的基础上,利用等价权原理,进一步发展到相关观测值的IGGIII方法.同样基于等价权,Yang等[38]利用方差分量的稳健估计来减弱粗差的影响.早期,在随机模型中的观测值的方差被认为是相等的[39].后来采用异方差假设来代替GNSS观测的不切实际的同方差.通常采用卫星高度角和载噪比作为观测值异方差假设的两个主要指标.其中高度角和观测值精度之间的关系可以用余弦函数或指数函数来充分描述[40].由于载噪比与GNSS观测值记录在同一个跟踪环路中,因此载噪比与GNSS观测值精度高度一致[41].
此外,双因子方差膨胀模型和双因子等价权模型同样有效地控制粗差对参数估值的影响[42].可从污染误差模型入手,研究最小均方差准则的参数稳健估计[43].杨元喜[44]根据多种抗差滤波及其性质构建抗差自适应滤波理论体系.同样地,基于方差膨胀的粗差处理方法经常被用于大地测量数据处理,例如变形分析[29]、基准变换[45]、GNSS完好性监测[46]、卡尔曼滤波[47].但是它们在模型结构不强、粗差较多的情况下,并不能完全消除粗差的影响.因此在多系统多频和城市峡谷环境等复杂条件下,对粗差处理方法的研究显得尤为重要.
3 两种粗差处理方法
3.1 数据探测
在复杂条件下,GNSS观测值通常不可避免地包含粗差.采用数据探测的方法对粗差进行后验处理,具体分为以下3个步骤[7-8]:
1)探测
采用整体检验,构造Tq统计量:
(1)

2)识别
采用标准化残差构造wi检验统计量:
(2)

3)调节
最后利用剩余的观测值重新进行最小二乘估计得到可靠的结果,并将其输出.

3.2 稳健估计
选权迭代法作为M估计的重要方法,同时是稳健估计中最为常用且计算简便的方法,其基本步骤如下:
1)建立数学模型
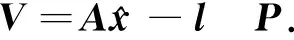
(3)
2)按最小二乘法求解参数估值及其残差
(4)
(5)
3)求解观测值的等价权矩阵,应用抗差最小二乘迭代计算,即
(6)
选定某一值ω作为迭代阈值(后续实验所讨论的阈值),当第k次与第k-1次迭代所得的估值之差的绝对值小于等于该值,则停止迭代.
(7)
4)最后求解
(8)
(9)
选权迭代法的关键在于选择权函数,最经典的是IGGⅢ方法.IGGⅢ方法的权函数pi确定如下:
(10)

(11)
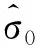
(12)
式中,q为多余观测数.
本文中讨论了面向复杂条件时ω、k0、k1的选取,由于过多地剔除观测值,会导致定位精度降低,因此可以通过迭代阈值(ω)来控制迭代次数,使稳健估计既具抗差性,又高效.
4 实际数据分析
为验证本文提出的粗差处理方案的有效性并评价定位精度,本文选取2021年年积日第288天24小时的5组西南地区滑坡监测数据进行实验.5组数据分别命名为Test1、Test2、Test3、Test4和Test5,其基线长度分别约92 m、143 m、53 m、133 m和75 m.实验主要利用GPS的L1+L2观测值和BDS的B1+B2 观测值进行处理,电离层延迟和对流层延迟分别利用Klobuchar模型和Saastamoinen模型进行改正,模糊度固定采用最小二乘模糊度降相关平差(LAMBDA)方法.具体的解算策略如表1所示.

表1 解算策略


表2 粗差处理方案


表3 观测数据的模糊度固定
限于篇幅,本文仅给出Test1的详细数据处理结果分析.在卫星定位中,可视卫星数越多,卫星几何构型越稳定.图1为Test1观测数据的GPS+BDS的可视卫星数和定位精度因子(PDOP).可以看出,观测数据的可视卫星数平均值为21,但卫星数存在明显的波动,接收卫星信号不太稳定,表明观测质量不佳.所有历元的PDOP值都大于1,其PDOP均值约1.6,有些历元的PDOP值超过3,因此整体看卫星的空间几何分布良好,但有时存在较差的空间结构.从整体看,随着卫星数的减少,PDOP的值随之增加.图2为Test1观测数据的卫星天空视图.可以发现GPS和BDS存在部分低高度角卫星,导致卫星信号存在反射、衍射和被阻挡的现象.因此在数据处理过程中设置了截止高度角为15°,剔除了不符合要求的卫星.
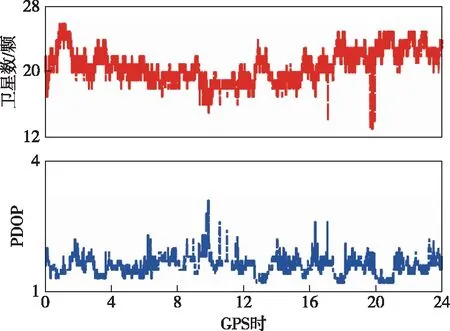
图1 Test1数据的卫星数和PDOP值Fig.1 Satellite number and PDOP value of Test1

图2 Test 1数据的卫星天空视图Fig.2 Skyplot of Test 1
图3和图4分别给出了A方案的双差伪距残差和双差载波残差.由图3可知,GPS和BDS的伪距残差绝大多数集中在10 m之内,其中GPS L2的伪距残差较大,可以看到在某些历元存有伪距粗差.由图4可看出,GPS和BDS的载波残差绝大多数集中在0.1 m之内.其中载波粗差没有完全剔除,而且较大的载波粗差会影响历元其他观测值,对定位结果产生严重影响.总之,需要加入合适的粗差处理方法来提高定位精度.
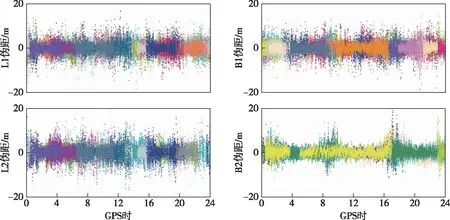
图3 A方案的双差伪距残差Fig.3 Double-differenced pseudorange residuals of scheme A
图5、6、7分别描绘了各个方案的定位误差结果.需要说明的是,定位结果中包含了固定解和浮点解的结果,以进一步整体评估其定位性能.由图5可以看出,无任何粗差处理方法的A方案定位结果是不太理想的,尤其是U方向的波动较为明显.对比图5,图6的3个数据探测方案都能探测到观测值的粗差,并进行粗差剔除,其中B方案在U方向上绝大多数历元的定位误差都比其他两个方案小.图7中大迭代阈值(ω)的稳健估计方案比小迭代阈值(ω)的稳健估计方案在相同的阈值(k0、k1)下有更为明显的收敛.其中在小阈值(k0、k1)时,E1方案在U方向上明显比E方案的误差小.同样E1方案对比其他稳健估计方案有更为明显的粗差处理效果,在卫星定位中表现了更好的定位性能.因此小阈值(k0、k1)结合大迭代阈值(ω)的稳健估计方案更适用于复杂条件的粗差处理.

图4 A方案的双差载波残差Fig.4 Double-differenced carrier residuals of scheme A

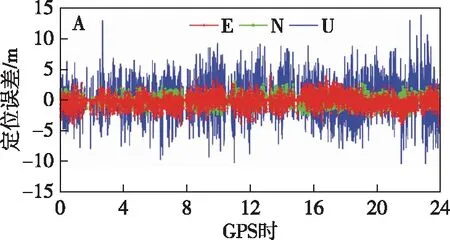
图5 A方案的定位误差Fig.5 Positioning error of scheme A

图6 数据探测方案的定位误差Fig.6 Positioning error of data snooping
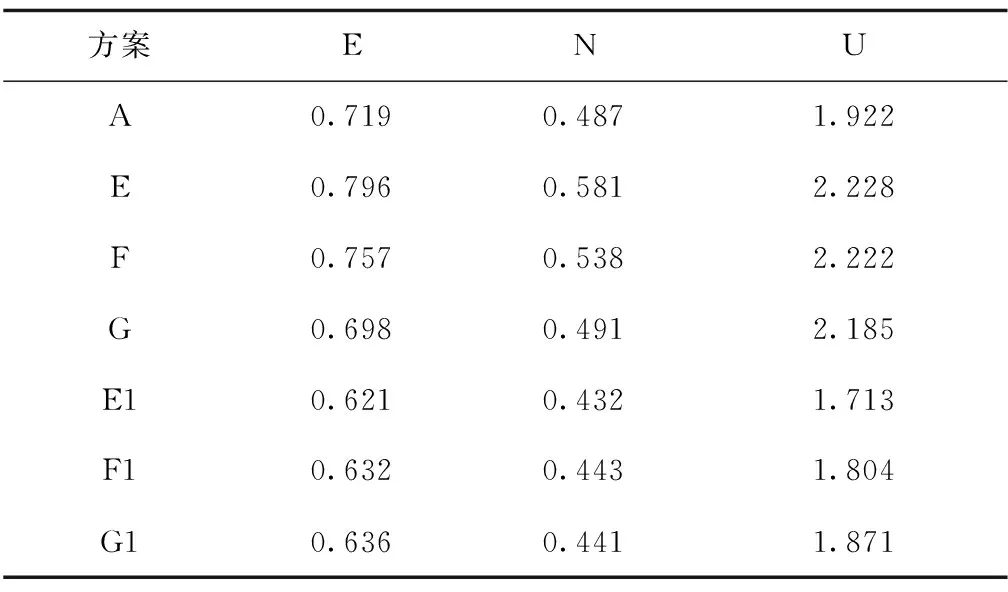
表5 稳健估计方案的定位RMSE统计
为验证各方案粗差处理的有效性,表6和表7分别列出数据探测与稳健估计的定位可用性,可以看到数据探测方案的可用性在任何的水平分量都优于A方案.同样稳健估计的E、F方案的定位可用性略差于A方案,但其他方案的定位可用性比A方案有所提升,其中E1方案在水平分量为2.0 m时,定位可用性达到96.50%.上述结果同样证明大迭代阈值(ω)配合小阈值(k0、k1)的稳健估计方案可以更好地识别粗差,对观测值权重的调整更为合理.
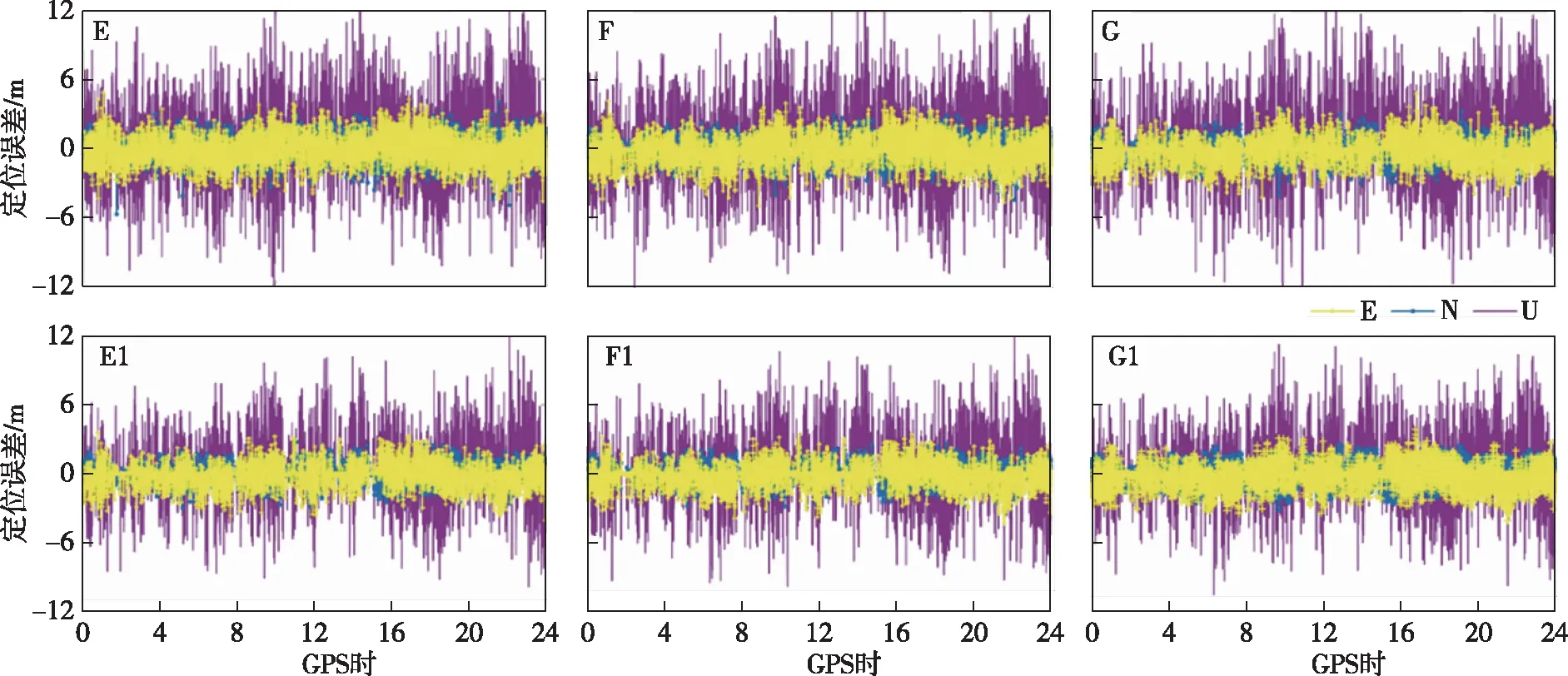
图7 稳健估计方案的定位误差Fig.7 Positioning error of robust estimation
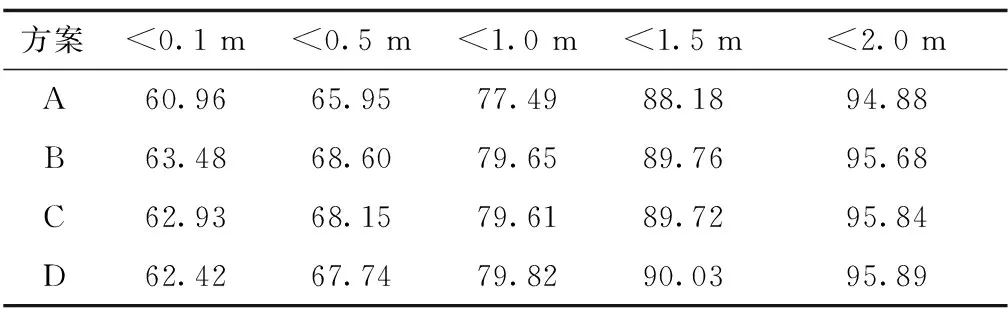
表6 数据探测方案的定位可用性

表7 稳健估计方案的定位可用性
5 结语
观测数据中含有异常粗差时,会对定位的精度和模糊度收敛产生严重的影响.本文系统研究了面向复杂条件时粗差处理的方法,针对复杂条件下的北斗/GNSS数据提出多种粗差处理方案,并以五组实验数据分析各方案的模糊度收敛速率,着重以一组数据对比分析各方案的粗差处理效果和定位性能.

综上,数据探测和稳健估计的处理粗差效果相当,但由于数据探测的粗差处理相对更精细化,因此在本文实验中数据探测可以表现出更好的适用性.
