线性非局部Drude模型的一种解耦格式的稳定性和收敛性分析
2022-12-16夏泽宇李茂军
徐 倩,夏泽宇,李茂军
(电子科技大学 数学科学学院,成都 611731)
纳米光子学是结合新兴纳米科技与光子学的一门学科,主要研究在纳米尺度上物质与光的相互作用[1],其中,金属纳米材料由于其独特的表面等离子体的振荡现象[2]成为研究的重点对象之一,在生物传感、癌症治疗、超材料、新型存储媒介等多个领域都有着重要作用[3-4]。
在纳米光子学中,常采用Drude模型来描述电子在金属中的输运性质[5],近几十年来,许多学者致力于研究该模型的空间离散化[6]。有限差分法(Finite Difference Method,FDM)由于其简单、易实现的特点被初步应用于求解Drude模型[7],在此基础上,Shibayama等[8]利用时域有限差分(Finite Difference Time Domain,FDTD)方法求解非线性Drude模型,通过对金属超材料中光脉冲传播和二次谐波的模拟,证明了该算法的可行性。此外,Hiremath等[9]采用有限元方法(Finite Element Method,FEM)基于弱形式进行了求解。Prokopeva等[10]利用有限体积法(Finite Volume Method,FVM)对Drude模型进行求解,以及对周期性超材料进行二维模拟。
对于Drude模型的数值计算方法,间断伽辽金(Discontinuous Galerkin,DG)方法是另一种可行的方法。Hesthaven[11]提出一种求解Drude模型的低存储高精度DG方法。Stannigel等[12]推动了Drude模型DG方法的发展。在此基础上,文献[13]提出利用时域间断伽辽金(Discontinuous Galerkin Time Domain,DGTD)方法来求解Drude模型。Fezoui等[14]设计了一种能够处理金属结构局部色散模型的DGTD方法,并给出了稳定性和收敛性分析。Li等[15]设计了一种用于求解超材料的时域麦克斯韦方程的节点DGTD方法。文献[16]与文献[17]针对非局部Drude模型分别提出了采用中心数值通量和迎风数值通量的DGTD方法。
本文针对线性非局部Drude模型,基于二阶向后差分(BDF)间断伽辽金(DG)方法提出了一种解耦的能量稳定格式,以期证明半离散格式和全离散格式的能量稳定性,以及全离散格式的最优收敛速率。
1 线性非局部Drude模型
考虑在凸域Ω×[0,T](Ω⊂3)上的一个线性非局部Drude模型,表示如下:
∂tH+∇×E=0,
(1)
∂tE-∇×H=-J,
(2)
∂tQ-∇·J=0,
(3)
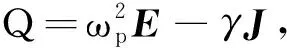
(4)
其中,未知量H,E,J和Q分别表示磁场、电场、电流密度和电荷密度,常数β是金属等离子体频率,γ是阻尼系数,ωp是金属等离子体频率。为了求解模型,给出初始条件和边界条件[18]:
H|t=0=H0,E|t=0=E0,Q|t=0=Q0,J|t=0=J0,n·J|∂Ω=0。
将公式(1)—(4)分别与H,E,Q,J做内积,可以得到:
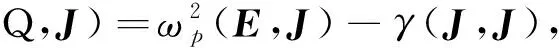
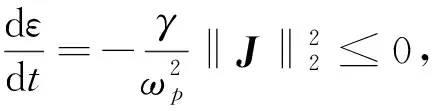
在TE模式下,E=E1e1+E2e2,H=H3e3,其中em,m={1,2,3}为笛卡尔基向量。记H=H3,从而在TE模式下式(1)—(4)可以改写为如下系统:
∂tH+(∂xE2-∂yE1)=0,
(5)
∂tE1-∂yH=-J1,
(6)
∂tE2+∂xH=-J2,
(7)
∂tQ-∂xJ1-∂yJ2=0,
(8)
(9)
(10)
为方便讨论,考虑二维矩形区域[a0,a1]×[b0,b1]以及周期边界条件:
u(x,y,t)=u(x+Δa,y,t),u(x,y,t)=u(x,y+Δb,t),
(11)
其中,Δa=a1-a0,Δb=b1-b0,u∈{H,E1,E2,Q,J1,J2}。接下来,将对系统(5)—(10)进行研究。
2 数值能量稳定性分析
2.1 半离散的DG格式
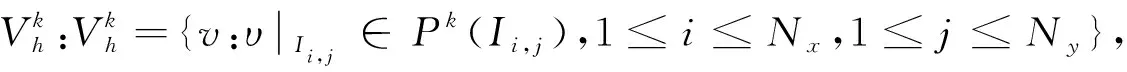
(12)
且满足边界条件:uh(x,y,t)=uh(x+Δa,y,t),uh(x,y,t)=uh(x,y+Δb,t),其中Δa=a1-a0,Δb=b1-b0,uh∈{Hh,E1h,E2h,Qh,J1h,J2h}。为证明(12)的能量稳定性,先证下面的引理。
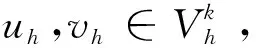
证明对等号右侧直接进行计算,可以得到
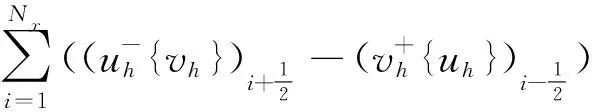
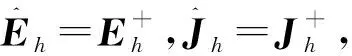
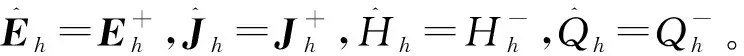
(13)
在所有单元Ii,j,i=1,2,…,Nx,j=1,2,…,Ny上把上面的6个式子累加,可得
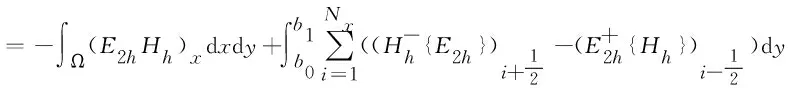
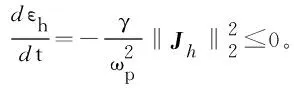
2.2 BDF-DG的全离散格式
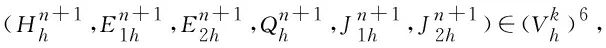
(14)
仍然满足边界条件:
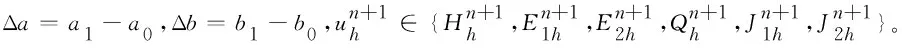
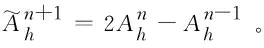
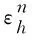

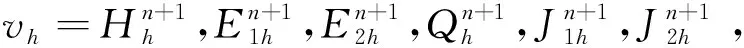
(15)
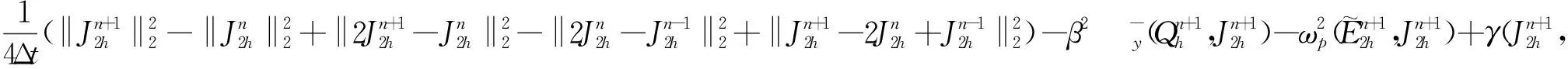
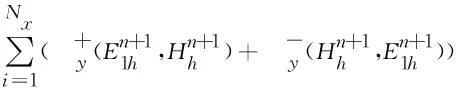
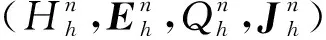
注2 为了求解二维系统(5)—(10),本文设计了一种解耦的BDF-DG格式,将(5)—(10)的6个方程简化为2个小系统。第一部分为(5)—(7),其未知量为磁场H和电场E,第二部分为(8)—(10),其未知量为电荷密度Q和电流密度J。即在(5)—(7)中,显式处理电流密度J,而在(8)—(10)中,显式处理电场E,因此这两个子系统是独立求解的。
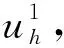
3 全离散格式的误差估计
3.1 投影算子及其估计
在本节将给出全离散格式(14)的误差估计。在此之前,介绍2个重要的投影算子。
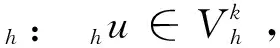
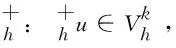
(16)
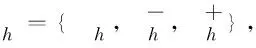
(17)
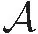
(18)
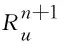
由于上式中所有项都是线性的,所以利用投影误差估计(16)和(17),可以得到
其中,时间误差是利用泰勒展开和柯西不等式得到的。
3.2 全离散格式的最优误差估计
在对全离散格式进行最优误差估计之前,需要对正则性做如下的假设:当k≥1 时,有
‖u‖l∞([0,T];Hk+1(Ω))+‖ut‖l∞([0,T];L2(Ω))+‖utt‖l∞([0,T];L2(Ω))+‖uttt‖l∞([0,T];L2(Ω))≤M,
(19)
其中u∈{H,E1,E2,Q,J1,J2},M是一个正常数,同时,用eu=hu-u来表示投影解与数值解的误差。
定理3 在满足式(19)的前提下,由全离散格式(14)得到的数值解(Hn,En,Qn,Jn)是唯一的,且当h 其中h0和Δt0是2个较小的正常数,C是与h和Δt的选取无关的正常数,n=2,3,…,Nt。 证明对于全离散格式(14)解的存在唯一性,直接通过方程的线性性,即线性方程组对应的齐次方程只有零解就能够证明。接下来证明误差估计,将投影格式(18)与全离散格式(14)作差,可以得到误差方程为: (20) (21) 由投影估计(17)与正则化假设(19) ,可以得到截断误差有如下估计 这并不满足PDE系统(5)—(10),因此必须加上源项f=7t6sin2(x)sin2(y),h=7t6sin2(x)sin2(y), 固定Nx=Ny=128,使空间误差可以忽略,分别取时间步长为Δt=1/16,1/32,1/64。此外为了简便起见,将原方程中的所有常数均设为1,得到解耦的BDF-DG法在h=π/64时的时间误差与收敛阶(表1)。由表1的数值结果可以看出,当Δt变小时,误差也会变小,数值格式在时间上是收敛的,并且可以得到数值格式的时间精度近似为2阶,与误差的理论分析一致。 表1 解耦的BDF-DG法在h=π/64时的时间误差与收敛阶 同时,取Nx=Ny=150,使空间误差可以忽略,分别取时间步长为Δt=1/16,1/32,1/64,得到解耦的BDF-DG法在h=π/75时的时间误差与收敛阶(表2)。由表2的数值结果可以看出,对于不同的h,当Δt变小时,误差也会变小,在时间上数值方法是收敛的,并且同样可以得到数值方法的时间精度近似为2阶,与误差的理论分析一致。 表2 解耦的BDF-DG法在h=π/75时的时间误差与收敛阶 固定Nt=1 000,分别取空间步长为h=π/5,π/10,π/20,π/40,得到解耦的BDF-DG法在Δt=1/1 000时的空间误差与收敛阶(表3)。由表3的数值结果可以看出,当h变小时,误差也会变小,在空间上数值方法是收敛的,并且可以得到数值方法的空间精度近似为2阶,与误差的理论分析一致。 表3 解耦的BDF-DG法在Δt=1/1000时的空间误差与收敛阶 为验证能量稳定性,选取计算区域为Ω×T=[0,2π]×[0,2π]×[0,30],初始条件为: 为了求解线性非局部Drude模型(5)—(10),本文采用了一种解耦的二阶BDF-DG方法对其进行数值离散,即用解耦的二阶BDF方法进行时间离散,结合DG方法进行空间离散,构造相应的解耦BDF-DG数值格式。从理论角度分别证明了DG空间半离散格式和全离散格式的能量稳定性。在全离散格式中,将整个系统解耦成2个较小的部分,即采用电流密度函数在电场方程中显式,且电场函数在电流密度方程中显式。这种“解耦”技术在系统较大的时候可以提高计算效率。此外还给出了全离散格式的最优收敛速率的分析。最后,通过一些数值算例进一步验证了该理论分析,即解耦的BDF-DG格式具有二阶时间和空间精度,且能量函数是递减的。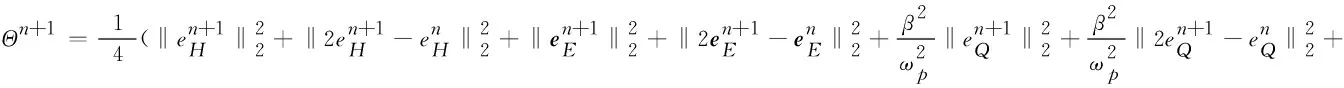

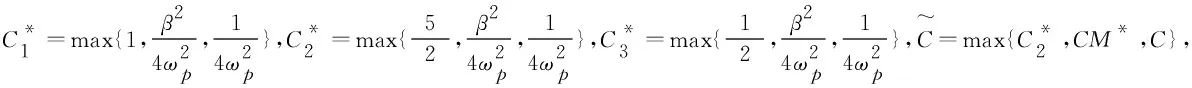
4.1 收敛性验证
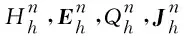



4.2 能量稳定性
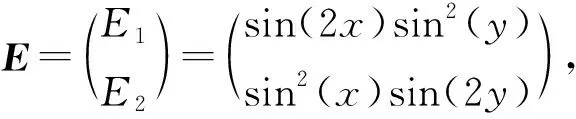
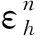
5 结 论
