双线隧道施工开挖错距对地表沉降的影响研究★
2022-12-16秦明泽曹文豪张学宇张申源
韩 驰,秦明泽,曹文豪,石 杰,陈 凯,张学宇,张申源
(1.南阳理工学院土木工程学院,河南 南阳 473000;2.枣庄职业技术学院 组织人事部,山东 枣庄 277000)
双线隧道进行开挖会造成隧道周围的地面严重松动变形,危及周围建筑物和居民安全。双线隧道的开挖一直被国内外业界人士所看重,降低开挖时对地表沉降的影响更是其中的难点。1806年,英国工程师布鲁尔于首次提出盾构法的施工原理,后经过改进,在气压的辅助下,完成了第一条盾构施工法的隧道[1]。自19世纪初以来,通过对国内外研究成果的总结可以分为经验公式法、模型试验法和数值模拟法。1969年,Peck发现隧道水土流失量基本等于开挖时地表水平沉降值,且地表沉降相似于呈现正态分布,并将隧道地表水平沉降曲线设置为沉降槽形式,后发现其沉降曲线呈现正态分布[2]。国内学者[3]对Peck公式进行了优化,并准确地预测了地表下沉量。在1984年Mair在参照盾构开挖监测数据的同时采用了离心模型来模拟软土地层隧道从而提出了盾构隧道施工造成地面沉降公式[4]。2005年,朱伟等研究盾构在穿过砂土层时运用了FLAC 3D软件,对隧道的埋深做出了分析、掌子面支撑力大小和砂土内摩擦角以及直径与地表沉降关系[5]。上述众多理论的提出也进一步发展和完善了双线隧道盾构施工的理论,同时国内学者对双线隧道开挖及稳定性[6-11]进行了较为深入的研究,为减小地表沉降影响的理论迈下了坚实的一步。
本文以洛阳地铁二号线某一区间隧道工程为背景,用FLAC 3D进行具体隧道的数值模拟并对圆形隧道断面及地表进行监测分析。对双线隧道开挖后、支护后的位移收敛进行检测和研究,科学的对隧道稳定性做出客观实际的规律总结,进而指导实际施工。
1 某隧道工程概况
洛阳轨道交通2号线(Luoyang Metro Line 2),是位于河南省洛阳市的一条标准地铁线路,工程的隧道位于该路段的LY45+000~LY47+980段内,该隧道为双线隧道,隧道采用双线四车道,左、右线分别长约1 830 m,2 170 m。工况地处中原,地质状况较好,地下水系较为简单,因此可以忽略地下水对施工进度的正常进行影响。
该隧道的断面为圆形断面,隧道的直径为8 m,埋深为44 m,地层标高为143 m~155 m。断面面积为50.27 m2。根据表1判断,该隧道为大断面隧道。

表1 按净空面积划分的隧道断面分类
2 支护方案及参数
隧道施工方式采用盾构法,隧道的支护方式采用盾构支护,首先,盾构机沿着目标线路分段,从启动井开始开挖土方。盾构机在前方土压力、盾构机内摩擦、千斤顶推力和侧向土摩擦阻力的作用下向前移动,随着盾构机向前推进,开始着手在盾构机尾部安装管片,盾壳在管片安装完成后将会从衬砌管片中脱出,且在盾尾脱空后立即开始注浆。其工程地质具体各土层数据以及支护结构参数(地质和支护参数)如表2所示。

表2 地质和支护参数表
3 模型建立
利用FLAC 3D对双线隧道进行开挖和支护模拟,针对岩土力学中材料的多样性和各种材料之间异同性,FLAC软件可择的本构模型可以简单的概括为以下几种:一种空模型、三种弹性模型、七种塑性模型此次采用摩尔-库仑模型(Mohr-Coulomb Model),该模型适用于普通土壤和岩石的力学行为(如边坡稳定和地下开挖),对应的材料特征为:松散胶结的颗粒材料、土壤、岩石、混凝土等。
FLAC 3D数值模拟过程中,有三部分需要严格制定,第一步是有限差分网格;第二步是选择本构模型并且输入材料特性即对材料进行赋值;第三步则是确定模型的边界和初始条件,数值模拟大概流程如图1所示。
模拟过程分为:数值模型建立、本构模型的选择、设置边界条件、初始条件施加、材料参数进行赋值、开挖、初次支护、设置监测点结果输出。本次建模尺寸为:X×Y×Z=114 m×100 m×42 m,最终得出模拟的完整图如图2所示。

建立初始应力状态的岩体结构模型后,把结果进行保存,开始进行隧道的开挖,本次采用每5 m一开挖一支护的方式,开挖时需要构建空洞模型。
确定边界时,将模型Z轴下端固定,上端无需固定,Z轴为-24 m,X轴左右边界均需要固定,X左端为-69 m,右端为45 m,Y轴前后两端均需固定,Y轴前端为0 m,后端为100 m。重力加速度的大小为10 m/s2,方向铅锤向下。本论文主要用的材料的物理参数有密度、内聚力、内摩擦角、体积模量、剪切模量、抗拉强度,具体如表2所示。
本次隧道开挖共设有五个错距方案:错距0 m、错距10 m、错距20 m、错距30 m、错距40 m。具体开挖示意图如图3所示。

4 结果分析
4.1 隧道的地表沉降和围岩的变形情况
以错距为0 m的隧道为例,隧道的竖直方向和水平方向位移云图如图4所示。
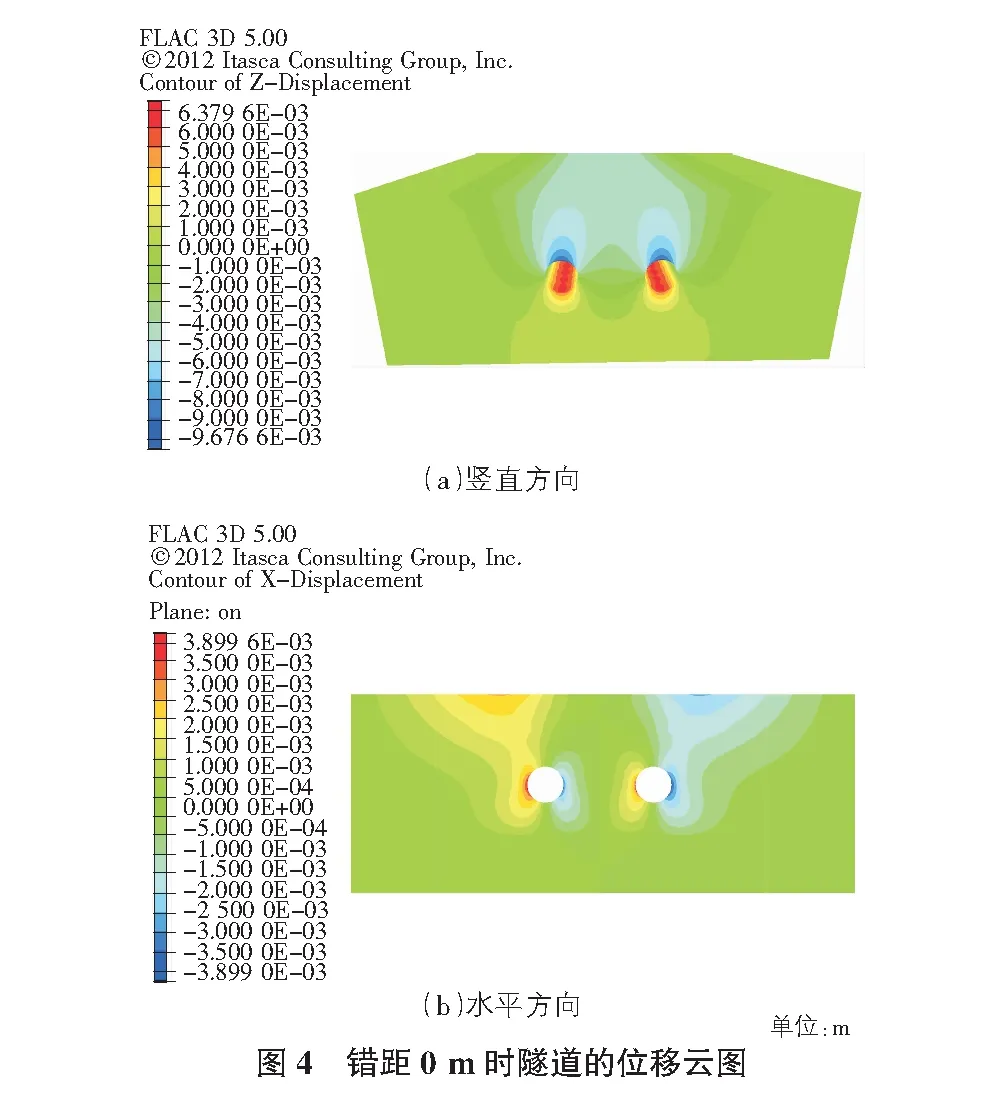
水平竖向位移变化进行横向、纵向对比情况具体见表3。
由图4,表3可知,错距为0 m时,两隧道位移基本沿中心线处于对称状态,其中仰拱最大下沉量为8.3 mm,拱顶最大隆起值为4.6 mm,横向断面收缩量(左右腰之和)为5.87 mm。

表3 水平和竖向方向位移收敛值
4.2 不同错距隧道的变形情况分析
错距为0 m~40 m时,双线隧道的断面变形情况如图5所示。由图5知,隧道最大变形量随错距先增大后减小,当错距为30 m时,隧道的变形量最大,其中竖向最大收缩量为14.3 mm,横向最大收敛值为6.3 mm。

4.3 不同错距隧道地表沉降变形对比分析
当错距为0 m,10 m,20 m,30 m以及40 m时,拱顶最大沉降量分别为50.3 mm,49.4 mm,48.0 mm,47.0 mm,46.3 mm。最大的沉降量出现在错距为0 m时,随着错距增大,地表下沉量逐渐减小,当错距大于20 m后,地表下沉趋于稳定。因此,在该地质和开挖条件下,20 m的错距是最有利的错距。不同错距双线隧道地表下沉情况如图6所示。

5 结论
1)通过FLAC 3D数值模拟对比可得:错距为0 m,10 m,20 m,30 m以及40 m时,隧道竖向收缩量分别为14.39 mm,14.2 mm,13.6 mm,13.4 mm,13.3 mm;横向收缩量分别为6.3 mm,6.2 mm,5.8 mm,5.7 mm,5.68 mm,均呈现递减趋势。
2)随着开挖错距的增大,双线隧道的地表下沉量逐渐减小,这与实际情况是相符的。
3)通过地表下沉及断面收缩情况的模拟发现,当错距为20 m时,为该地质及开挖条件下的最优错距。
