浅谈高校数学教学过程中应强化的几个方面
2022-12-16于勇
于 勇
(攀枝花学院数学与计算机学院(大数据学院),四川 攀枝花 617000)
高校数学教育教学随着高校人才培养目标的不断调整正在逐步由早期基础理论知识体系的学习向加强数学创新及应用能力培养方向转变。国家在部分高校实行强基计划,要求在本科阶段培养并夯实基础学科能力素养,并注重培养学生综合素质,加强科技创新能力的培养。实现这一目标,高校数学教育教学应当以新时期社会发展对数学专业人才的需求为出发点,对教学内容和教学方式进行改革,最直接、根本的方式就是从数学教学环节上进行优化,不断丰富教学内容,创新数学教育教学方式,在日常教学活动中应强化以下几个方面。
1 强化课题内容的延伸和拓展
高校数学教育教学的资源多来自教材,各门课程自成体系,课程内容多以理论为主,缺少应用方面的案例以及各知识点的拓展,同时缺少学科之间知识点的过渡,使得学科之间联系脱节,导致教学内容的适用性不断降低,学生对知识点的认识相对狭隘,只能机械地运用公式、定理、结论去解决相对固定的一些题型,严重影响了学生对所学知识的灵活掌握和运用以及运用所学知识分析、解决实际问题的能力,阻碍了学生对数学知识认识的整体性以及数学知识的运用能力。同时大多数学生在学习过程中感到数学知识枯燥乏味,认为所学数学知识没有用处,逐渐失去了对数学学科学习的兴趣。
作为数学教师,首先应在备课环节强化教学课题涉及内容的丰富和完善,根据相应的知识点,深入剖析知识点所涉及问题的本质,适时对课题内容进行延伸和拓展,同时注重强化不同课程知识点的衔接,努力拓宽学生的知识宽度和认识深度[2];其次,要在教学内容中有意识地增加与知识点相关的案例,引导学生用所学的数学知识、方法去分析、解决这些案例,这样不仅提高了学生分析、解决实际问题的能力,而且能够有效提高学生学习数学的信心,激发学生学习数学的兴趣和热情,从而达到提高学生能力素养,增强学生创新及应用能力的目的。
例如在常微分方程教学过程中,教师可以适时引入捕食者-被捕食者系统的Volterra模型:

通过对建立数学模型的思路进行分析,引导学生将所学知识运用于实际问题,不仅可以巩固和拓展学生对知识点的理解,而且可以极大提高学生的学习热情和主动应用数学知识的意识和能力。
又如,在线性代数课程教学中,由于该课程大量的知识点均缺乏与其他课程知识点的衔接,显得孤立、无用,学生学习积极性不高。针对问题,教师在教学中就应当主动将知识点与其他课程知识点进行衔接,梳理知识点内在的联系。
如向量内积的教学,我们可以通过物理学中力的做功以及解析几何中几何向量的数量积进行引入,定义数组向量和的内积,并且有与正交。此时我们可以进一步将知识点拓展到高等数学中傅里叶级数部分的三角函数系
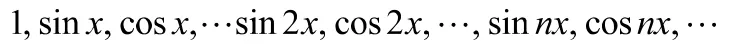
2 强化数学原理的证明和理解
目前很多高校的数学教学淡化了一些重要定理、性质的证明,目的是为了提高教学内容的效率,这样的教学只会使学生机械地掌握数学理论和方法,失掉了数学教学的本质,致使学生对教学内容感到枯燥无味、毫无兴趣,失去了学习的动力,失去了灵活掌握和运用数学知识的能力,并严重阻碍学生后期的发展,严重影响了学生数学能力的提高[1]。
数学是自然科学,根植于自然,知识体系的形成和发展就是一个不断发现的过程,有着深厚的理论背景。数学原理的背景、发现的过程、理论体系的形成体现了数学发现的过程[1],对这一过程进行探索,就是探索数学本身。
人们如果要深刻地认识事物就要认识事物的内在规律,而原理是对事物间内在联系和基本规律的科学表述[4],所以,想让学生学好数学,运用好数学知识,数学的基本原理应该成为学生学习数学的核心内容。
数学教学中我们不能面面俱到、循规守矩,只有抓住教学课题的核心内容,才能纲举目张。而核心内容其实就是我们要讲的数学原理,整个知识体系就是围绕着这一原理展开的。
数学知识来源于生活,经过高度抽象形成的数学原理主要包括数学概念以及由此产生的性质和定理[2]。在数学教学中对原理的理解是灵活掌握运用数学知识的基础,当学生理解了这些定理、公式的来龙去脉,学生就可能会想出更新的东西。数学原理的深入理解是证明或计算的前提,会使学生在解决问题过程中目的明确,思路清晰,对数学方法的使用更加得心应手,可以根据其所掌握的数学基本原理去解决实际生活中的数学问题。
教学中发现学生普遍惧怕证明题,惧怕综合性的题目,解题方法普遍较单一、缺少灵活性,解题过程中畏手畏脚,不敢创新,就是缺乏对数学基本原理理解掌握的表现。
教师应当从自己的学习、从事研究的经验中不断地去总结、归纳、剖析对数学理论掌握理解的途径,抓住问题的本质并结合学生的认知过程,制定教学方案,并付诸教学实践。
3 强化学生主动思考和探究环节
主动思考和探究问题的能力是一种综合能力,表现为当个体面对不同的实际问题时,能主动运用不同的思维方式、方法和技巧去探索和解决所面临的问题。庞加莱说,“我们用逻辑进行证明,凭直觉创造”[1],在数学教学中,教师引导学生主动思考和探究应贯穿于整个教学过程,教师针对教学内容适时提出问题,创设环境,积极引导学生进行思考,主动寻求解决问题的途径和方法,充分发挥学生学习的主动性和创造性,能够有效地培养学生的直觉思维和逻辑思维能力[5]。在解决数学问题的过程中,直觉思维是数学发现的方法,而逻辑思维则是解决问题的方法,因此,在具体的数学教学过程中,应加强这两种思维的互补作用。
首先,为了更好地激发学生的主动思考和探究问题的积极性,数学教学应重视学生的“学前准备”。在进行教学之前,教师应根据课题内容以及学生现有的知识水平,结合学生认知问题的一般规律以及课题内容涉及的知识体系,构造出相应的问题,提供丰富的背景材料,作为学生课前的学习任务,充分挖掘学生的潜力。这样才能让学生更多地参与到具体的教学活动过程中来,使每一个学生都能在原有的认知水平上得到最大限度的发展[5]。
其次,在教学过程中,始终围绕知识体系,恰当地设置教学环境,促使学生作整体性思考,让他们在面临问题时,注意首先从整体上考虑其特点,着眼于从整体上揭示出数学对象的本质及内在联系,对各种信息作综合性考虑。同时创设问题情境,以激发学生的好奇心和发现欲,使学生在发现问题和探索问题的过程中进行积极的思维[3]。通过适当推迟做出结论的时机,留出足够时间让学生们自己去认真地思考一下问题,给学生留下直觉思维的空间,其间通过条件的设置对学生进行引导,去探索问题的内部规律[4]。
教师还可以根据教学内容,为学生提供一些未来的探究空间。如我们在讲授数理统计课程时的两个重要的抽样分布分布和分布,我们可以告诉学生:这些重要的抽样分布是人们在研究随机变量的函数的分布时得到的结论,在掌握随机变量的函数的分布的方法的基础上是有可能获得更多有用的抽样分布的。
通过激发学生主动思考和探究问题,可以有效地增强学生的主体意识,从而达到开拓思维、提高创新能力的目的[3]。
任何形式的教学理念的创新都需要付诸实践,实践是检验真理的唯一标准,对于数学教育教学实践中发现的问题,则是推动高校数学教育教学持续创新的动力[3],数学教师应通过不断丰富数学教育教学内容,创新高校数学教育教学方式,最终实现高校数学教育教学质量的全面提升。
