适用于任意多进制的DAC通用结构

刘 超,陶 敏,宿 刚,李德辉,郑 伟,石景龙

(吉林大学 电子科学与工程学院,长春 130012)

0 引 言

DAC(Digital-to-Analog Converter)作为沟通数字和模拟的桥梁,其在远程通信、发光二极管驱动、扫频仪、密集波分复用、低功耗蓝牙设备和信号调制器等需要将数字信号转换成模拟信号时,具有重要的应用价值[1-7]。在一般的DAC结构中,输入数字量都是二进制逻辑的。一位二进制数只能表示一比特的信息量。而多进制逻辑与二进制逻辑相比,在相同的位数下携带有更大的信息量。由于多进制逻辑信息具有密度大的优点,使其在诸如电信号和光信号调制、信号传输等方面得到了广泛的应用[8-13]。将多进制逻辑引入DAC结构设计中,将使DAC在相同位数下,得到更高的分辨率。三进制DAC作为多进制DAC中结构最简单的一种,目前已有许多对其研究报道。Choi等[14]设计了一个4位的电流舵结构三进制DAC,不仅具有更佳的分辨率,还具有功耗低和尺寸小的优点。但该基于电流舵的三进制DAC结构中,一个N位DAC需要N个不同大小的参考电流源,并且这N个参考电流源的电流大小呈现指数级递增,这导致参考电流源的个数和匹配度同时制约了位数N的增加。

笔者提出了一种适用于任意多进制数字输入的电压输出型DAC结构。对N位三进制的DAC,只需要两个参考电压源；对N位M进制的DAC,只需要M-1个参考电压源,并且参考电压源的电压大小是线性增长的。这种DAC结构采用了电阻网络结构,其想法来源于传统的二进制R-2R梯形电阻网络结构的DAC[15]。通过对R-2R梯形电阻网络结构电压输出型DAC进行改进,使该DAC结构通过简单的改变就可以适用于任意的M进制数字输入DAC的设计。

1 DAC结构

1.1 二进制R-2R DAC结构

传统N位二进制R-2RDAC结构[15]原理如图1所示。图1a所示的电阻网络中只含有阻值R和2R两种电阻,电压源标号dxVREF(1≤x≤N-1,输入数字量dx取值为0或1)为图1b所示的单刀双掷模拟开关(SPDT：Single-Pole Double-Throw Analog Switch)与参考电压源VREF组合结构的简化形式。如图1b所示,dx对SPDT进行控制：当dx=0时,SPDT接通到地,则dxVREF=0；当dx=1时,SPDT接通到VREF,则dxVREF=VREF。因此SPDT输出的电压可统一表示成dxVREF。

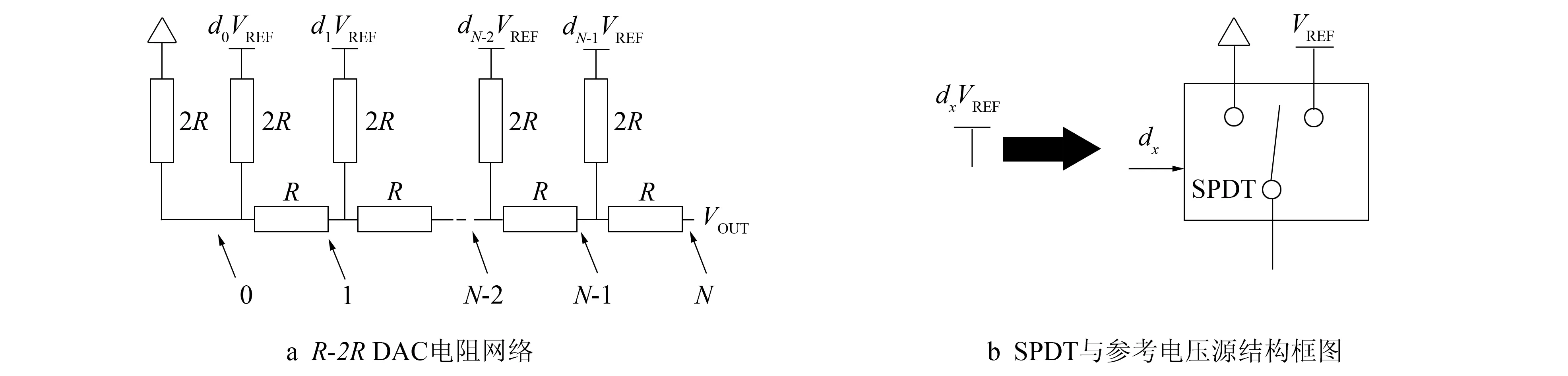
图1 R-2R DAC原理图Fig.1 R-2R DAC Schematic diagram

根据戴维南定理,从图1a中箭头指向的0～N中任意一点的左侧等效电阻均为2R。从1～N-1点中任取一点k(1≤k≤N-1),得到如图2a所示的第k点局部等效电路。如图2a所示,k点左侧等效电阻为2R。再假设图2a中的k点左侧等效电压为Vk。

图2 R-2R DAC等效电路Fig.2 R-2R DAC equivalent circuit

根据线性叠加定理,得到第k+1点左侧等效电压Vk+1与第k点左侧等效电压Vk、第k个电压源dkVREF的迭代关系

(1)

根据式(1),得到图1a中箭头所指的输出电压VOUT所在的点N处左侧等效电压为

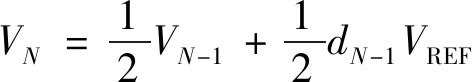
(2)

对式(2)进行多次迭代,得到图1a中输出点N处左侧最终的等效电压为

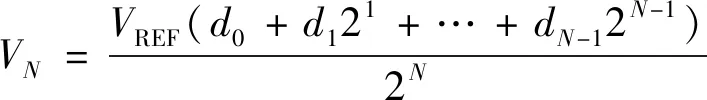
(3)

图1a中的DAC输出点N处左侧的等效电压为VN,等效电阻为2R。因此,R-2RDAC输出端的等效电路如图2b所示,从输出电压VOUT处向左边看,电路由电压源VN和电阻2R串联组成。式(3)描述了二进制R-2R梯形电阻网络电压输出型DAC由数字量到模拟电压的转换函数关系。

1.2 任意多进制的DAC结构

对任意多进制的电压输出型DAC一般结构根据二进制R-2RDAC结构进行改进,其原理图如图3所示。其基本结构与二进制R-2RDAC相比添加了一组电阻RC，并且对M进制的电压输出型DAC,输入数字量dx(0≤x≤N-1)取值为0～M-1。因此,对应的参考电压为M-1个,模拟开关为单刀M掷模拟开关(SPMT：Single-Pole Muti-Throw Analog Switch)。电压源标号dxVREF为图3b所示M-1个电压源和SPMT结构的简化形式。如图3b所示,dx对SPMT进行控制,当dx为i(0≤i≤M-1)时,SPMT与iVREF接通。例如,当dx=2时,SPMT接通到2VREF。因此SPMT的输出电压可统一表示成dxVREF。不同的参考电压组合,经过电阻网络后,在图3a中箭头所指向的N点产生输出电压VOUT。

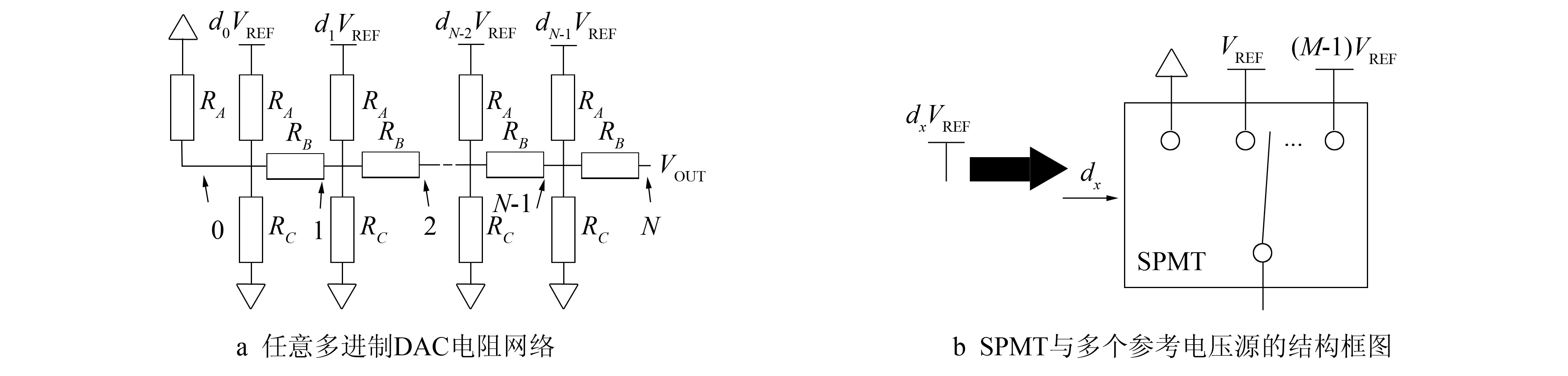
图3 多进制DAC原理图Fig.3 Schematic diagram of DAC suitable for arbitrary radix

选取特定的RA、RB和RC电阻阻值使其满足：从图3a中箭头指向的0～N中任意一点左边的等效电阻均为RA。因此,如果从1～N-1中任取一点k(1≤k≤N-1),则其左侧等效电阻为RA。任意M进制DAC等效电路如图4所示。

图4 任意多进制DAC等效电路Fig.4 DAC suitable for arbitrary radix equivalent circuit

图4a为第k点局部电路原理图。根据线性叠加定理,k+1点处左侧等效电压由第k点左侧等效电压Vk与第k个参考电压dkVREF加权组成

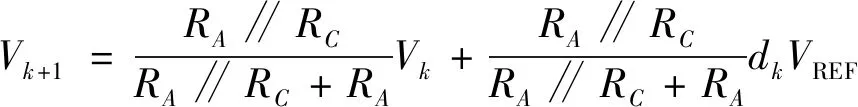
(4)

对M进制数字输入的DAC,在Vk和dkVREF的作用下,k点处的电压应等于Vk衰减1/M与dkVREF衰减1/M的和。此外,根据戴维南定理,图4a中k点处的加权电压等于k+1点左侧等效电压。因此,k+1点处左侧等效电压Vk+1应该满足

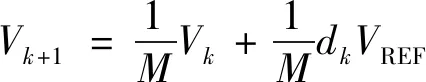
(5)

对比式(4)和式(5),可得到RA与RC满足

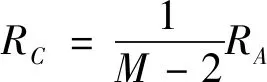
(6)

考虑到k+1点处左侧的等效电阻应等于RA,因此有

RA=RA∥RA∥RC+RB

(7)

将式(6)代入式(7),化简得到

(8)

根据式(6)和式(8),得到RA、RB和RC的数值关系。当M=2时,由式(6)可知RC的值为无穷大,相当于不连接RC；由式(8)可知RB=0.5RA。根据图3a、式(6)和式(8),容易发现在M=2的特殊情况下,任意多进制DAC结构即为二进制R-2RDAC结构。因此,任意多进制DAC结构为传统R-2RDAC结构的拓展。

对M>2时的一般情况,根据式(5)迭代计算得到图3a中N点左侧的等效电压为

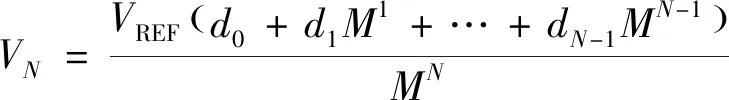
(9)

式(9)描述了M进制的电压输出型DAC结构由数字量到模拟电压的转换函数关系。其中M可为任意大于1的整数。式(9)表明,N位M进制数字输入的DAC可以实现分辨MN阶不同的电压。相比于二进制数字输入的DAC只能分辨2N阶不同的电压,任意多进制DAC的分辨率随着进制数M的增大而显著提高。而且该DAC结构简单,设计难度不随位数N和进制数M的增加而增大。由于每一级电阻网络和参考电压的结构都相同,拓展位数时仅需简单地对相同结构的电阻网络和参考电压结构进行相应个数的拓展。而拓展进制数时,仅需要对模拟开关的输入通道数和参考电压进行相应个数的拓展。在进行位数拓展和进制拓展时,结构也没有明显变复杂。因此,可以方便地利用该结构设计多进制和高位数的DAC。

2 三进制电压输出型DAC实验

2.1 电路设计

选取N=8、M=3,对笔者提出的DAC结构进行功能验证。利用分立元件和集成电路芯片设计8位的三进制电压输出型DAC电路模块。当M=3时,根据式(6)和式(8),RA、RB和RC满足RB=2/3RA以及RC=RA的数量关系。选取RA=30 kΩ,则RB=20 kΩ,RC=30 kΩ。设计的电路原理如图5所示,该电路有两个参考电压源VREF和2VREF。选取VREF=1.25 V,2VREF=2.5 V。

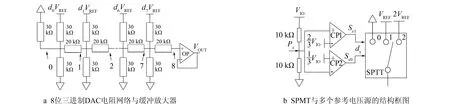
图5 8位三进制DAC原理图Fig.5 8-trit ternary DAC schematic diagram

为使微控制器和可编程门阵列等具有三态引脚的控制电路能对该DAC进行控制,输入接口进行了

特殊设计,使三态引脚Px(1≤x≤7)输出的电平与三进制DAC的数字输入量dx取值一一对应。如图5b所示,每个三态引脚连接到10 kΩ上拉电阻和10 kΩ上拉电阻中间。上拉电阻的另一端接高电平VIO,下拉电阻的另一端接地。三态引脚Px的输出状态与DAC的输入端dx的对应关系如表1所示。三态引脚Px同时连接到两个比较器CP1和CP2的输入端。当三态引脚Px输出为低电平时,CP1的输出端Sx1为低电平,CP2的输出端Sx0为高电平,则dxVREF=VREF。当三态引脚Px输出为高阻态时,两个比较器CP1和CP2输出均为低电平,则dxVREF=0。当三态引脚Px输出为高电平VIO时,CP1的输出端Sx1为高电平,CP2的输出端Sx0为低电平,则dxVREF=2VREF。

由于图5a中的箭头所指向点8处左侧的等效电阻的30 kΩ电阻不可忽略,因此连接一个缓冲用的放大器OP,使电压从图5a的VOUT点处输出。将N=8、M=3和VREF=1.25 V代入式(9),得到8位三进制的电压输出型DAC的数字量到模拟电压的转换函数

实际制作的8位三进制DAC电路模块如图6所示。其大小紧凑,长为54 mm,宽为27 mm。

图6 8位三进制DAC实物图Fig.6 Picture of the 8-trit ternary DAC

2.2 数据与分析

对实际DAC电路静态数据进行测试。8位三进制DAC理论上可分辨多达6 561个不同的电压值,因此选择性地等间隔选取243个点的电压进行测量。电压测量仪器选择吉时利公司的六位半高精度万用表,保证测量数据的可靠性和准确性。该DAC的测试结果曲线如图7所示。

图7a给出了实际测试输出模拟电压值随输入数字量的变化关系,以及理论输出模拟电压值随输入数字量的变化关系。由图7a可看出,实际测试电压值与理论电压值在整个数字输入量变化范围内随输入数字量变化的总体趋势一致,从而验证了笔者提出的DAC结构的正确性。图7b给出了模拟电压实测值与理论值的误差随输入数字量的变化关系,可看出最大误差接近33 LSB(Last Significant Bit)。图7b中出现的误差,主要有3个来源：由电阻网络中的电阻值误差、模拟开关的导通电阻和参考电压源内阻等电阻原因间接导致误差；缓冲放大器输入失调电流和缓冲放大器输入偏置电流等电流,间接导致误差；参考电压源的电压值存在误差和缓冲放大器输出失调电压等电压,直接导致误差。可以采用集成电路设计该DAC降低误差。

此外,从图7b中可看到,误差随输入数字量呈现阶跃变化现象。前两次阶跃现象出现在DAC的MSB(Most Significant Bit)发生切换时。这是由于MSB的权重最大,其对电阻值误差较敏感,导致其对电压误差的影响较大。从图7b还可看到,还存在第3次误差的阶跃变化,其原因是电阻网络型DAC本身存在的本征非单调特性。与图7对应的部分数据,如表2所示。

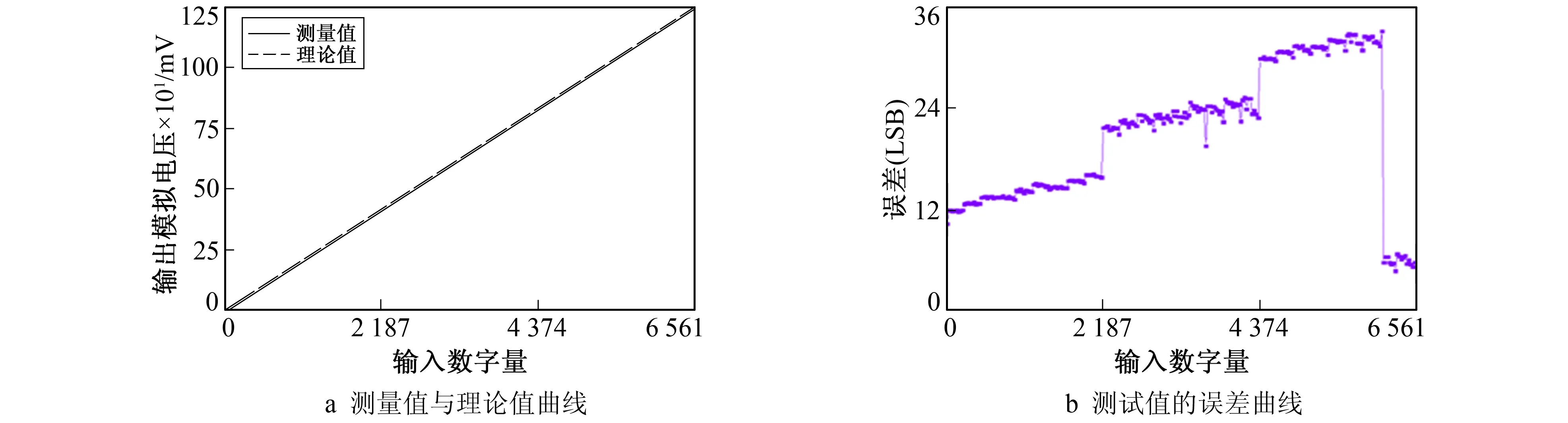
图7 数据曲线Fig.7 Data curve

3 结 语

笔者根据传统的二进制R-2R电阻网络型DAC,提出了一种新的DAC结构,并逐步推导出各个电阻阻值应该满足的关系,使其能推广到任意的多进制DAC。对不同进制的DAC,其结构基本相同,区别主要在于电阻网络中电阻值和参考电压源的个数不同。为验证该DAC结构的基本功能而构建的8位三进制DAC电路可产生38种不同的模拟电压值。而8位二进制DAC只能产生28种不同的模拟电压。因此,8位的三进制DAC的分辨率相当于8位二进制DAC的 25.6倍。该结果显示了多进制逻辑在DAC结构设计方面的应用潜力。