多次冲击波作用下加筋板动态响应数值模拟研究

2022-12-14张劲夫翟红波田魏婧刘永寿

兵器装备工程学报 2022年11期

崔皓,张劲夫,翟红波,田魏婧,刘永寿

(1.西北工业大学力学与土木建筑学院，西安 710129； 2.西安近代化学研究所，西安 710065)

1 引言

加筋板作为常见的防护结构，在各类装甲车辆的车门结构、防护结构中拥有广泛的应用。在复杂的战场环境中，装甲车辆可能受到地雷、炸弹等多次爆炸载荷冲击而形成损伤甚至破坏。研究结构受多次爆炸载荷的动态响应有助于装备的防护设计和提高人员在危险的爆炸环境中的生存力。从20世纪60年代至今，有大量学者开展了有关爆炸载荷下结构的动态响应研究。Menkes等[1]首先提出了在脉冲载荷作用下固支梁结构的失效模式，并总结为：塑性大变形(mode Ⅰ)、支撑处的拉伸撕裂(mode Ⅱ)、支撑处的横向剪切破坏(mode Ⅲ)。Teeling-Smith等[2]率先采用试验的方法，观察得到了固支圆板结构的变形历程，并细化了失效模式。侯海量等[3]研究了加强筋的相对刚度对加筋板变形模式的影响，并给出了加筋板处于塑性大变形(mode Ⅰ)阶段时，塑性变形量随脉冲载荷变化的经验公式。李帅等[4]通过数值仿真的手段，探究了不同加强筋平板结构在一次爆炸冲击载荷下的动态响应，发现加强筋数量越多，加筋板的抗冲击能力就越强。Langdon等[5]采用试验和数值仿真相结合的手段，研究了一次冲击下加筋板的动态响应，并观察到了局部拉伸撕裂的失效模式。Zhao等[6]利用仿真与试验联合的方法，研究了外加筋板与内加筋板在相同载荷条件下的动态响应，发现外加筋板的极限挠度小于内加筋板，外加筋表现出整体弯曲变形的失效模式，内加筋板则表现为腹板失稳的失效模式。代利辉[7]研究了水下爆炸载荷下固支方板的动态毁伤模式，证明了固支方板临界破裂压力与平板自身几何尺寸和炸药距平板的距离有着直接关系。梁浩哲[8]采用试验与仿真结合的方法，研究了一次深水爆炸下凸型加筋锥柱壳结构的破坏模式，获得了3种不同的破坏模式，并揭示了不同破坏模式之间的演变与转换机理。琚泽宇[9]开展了一次爆炸载荷下加筋板的抗爆性研究，明确了不同构型加筋板在一次爆炸载荷下的动态响应特点，研究结果对金属板的抗爆性设计具有参考价值。沈晓乐等[10]采用试验手段研究了加筋板结构在冲击波和气泡联合作用下的动态响应，发现纵向加强筋能够很好地反映加筋板结构受冲击的动态响应特性。苗润等[11]研究了复合材料加筋板的抗侵彻能力，指出复合材料加筋板具有加筋结构和复合材料的优势，可以很好地降低半穿甲弹体的侵彻能力。赖鸣等[12]研究了不同加筋结构在水中接触爆炸下的破损规律，发现增加加强筋的高度能够有效地降低破口面积，且接触爆炸时局部破坏先于整体破坏。Mohammad等[13]利用数值模拟的方法研究了多次冲击载荷下多层板结构的动态塑性响应，发现M-Ar组合材料的抗爆性低于M-Al和DM-AlAr-1/2。Yao等[14]将无量纲分析方法引入爆炸载荷下的板的动力响应研究中，提出了一种爆炸载荷作用下固支板的无量纲数，并给出了预测不同爆炸载荷条件下板动态响应的经验表达式。

学者们已经对一次爆炸冲击载荷下加筋板的动态响应开展了广泛的研究，但是对其在多次冲击波作用下动态响应的研究却相对较少。目前多次冲击下加筋板累积损伤机理不清，累积损伤表征手段不足。同时，结构受多次冲击导致失效的问题在工程实践中十分常见，因此亟需深入研究结构在多次冲击作用下的动态响应规律。此外，本文中还讨论了加强筋构型、边界条件对加筋板毁伤效应的影响。

2 模型建立及计算

为验证数值模拟的准确性，分别采用Conwep算法和ALE算法分别进行多次冲击波作用下加筋板的建模及动态响应计算。

2.1 Conwep算法

2.1.1Conwep算法载荷条件

典型的TNT爆炸冲击波曲线如图1，在冲击波抵达前，压强等于大气压强P0，当冲击波接触结构表面时，与结构接触处的压强会阶跃达到峰值Pmax，随后迅速以指数形式衰减，直至出现负压峰值，在此后的一段时间，负压会逐渐衰减至大气压强。

图1 爆炸冲击波曲线

Conwep算法使用关键字*LOAD_BLAST_ENHANCE和*LOAD_SEGMENT_SET进行加载。该方法不需要炸药模型和介质模型即可进行计算，极大地提高了计算效率。

2.1.2Conwep算法模型建立

选取双十字加筋板为研究对象，其几何参数为长l=90 mm，宽b=90 mm，板厚H=3 mm，加强筋高h=7 mm，加强筋厚t=3 mm。由于防护结构常常采用焊接等方式固定在装甲车辆上，故采用四端固支的边界条件进行数值模拟。加筋板采用Shell单元，如图2所示。炸药设置在加筋板正上方150 mm处，每次爆炸的TNT质量为120 g，共设置4次爆炸。

图2 双十字加筋板有限元模型示意图

在不同冲击次数间利用关键字*STRESS_INITIALIZATION进行重启动分析，实现应力、应变、残余挠度等状态参量在不同冲击间的传递。因为现实中结构受冲击能够在极短时间内完成自由振动的卸载，且结构在极短时间内受到多次冲击的可能性较小，所以在每次冲击后结合重启动技术,利用关键字*DAMPING_GLOBAL、*DEFINE_CURVE添加阻尼，实现冲击后振动的卸载，使结构处于稳定状态，并将每次冲击后的稳定状态作为下次冲击的初始状态，图3为多次冲击数值模拟流程框图。

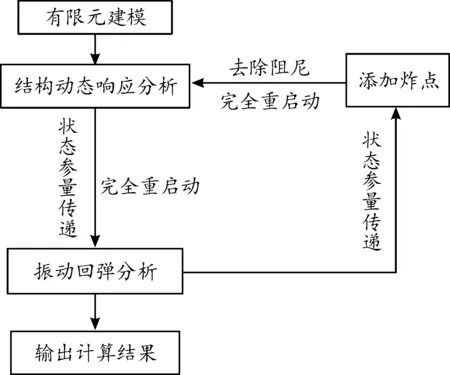
图3 多次冲击数值模拟流程框图

2.1.3材料模型

(1)

式(1)中：A为材料的屈服应力；B与n为材料的应变硬化系数和应变硬化指数；m为温度软化指数；C为应变率硬化系数。

Johnson-cook失效模型包含应力状态项、应变率状态项和温度状态项。其中，失效应变可表示为：

(2)

式(2)中：D1～D5为材料常数；p为压力；其他参数物理意义同式(1)。

(3)

当损伤量D>1时，出现破坏且单元被删除。

采用4340钢的材料参数及破坏参数进行多次冲击计算[15]，如表1所示。

表1 4340钢的材料属性及失效参数

2.2 ALE算法

2.2.1ALE算法模型建立

TNT质量、炸点位置、加筋板几何尺寸、材料属性及边界条件与Conwep算法保持一致。在ALE算法中加筋板采用Lagrange网格，TNT与空气域均采用Euler网格建模，采用流固耦合算法进行计算。ALE算法有限元模型的示意图如图4。

图4 ALE算法有限元模型示意图

炸药采用关键字*MAT_HIGH_EXPLOSIVE_BURN定义，选用*EOS_JWL状态方程描述爆炸过程中轰爆产物的体积与压力的变化关系，该状态方程的函数表达式为：

(4)

式(4)中：P为爆炸压力；E为单位体积炸药的初始内能；V为轰爆产物的体积；A、B、R1、R2、ω为炸药特性参数。

P=C0+C1μ+C2μ2+C3μ3+(C4+C5+C6μ2)E

(5)

流固耦合关系采用关键字*CONSTRAINED_LAGRANGE_IN_SOLID定义。

仍采用重启动实现状态参量在不同冲击次数间的传递，每次冲击后，利用重启动添加阻尼实现自由振动的卸载，使结构处于稳定状态后再次进行冲击波加载。每次冲击后，对TNT及空气域重新进行建模并赋予属性，实现多次冲击波的加载。

3 多次冲击模拟结果及分析讨论

3.1 失效模式分析

图5为不同算法下每次冲击后加筋板处于稳定状态的残余挠度云图，由图5可以清楚地看到，在不同算法下，加筋板受到初次冲击波作用，永久塑性变形首先发生在加筋板的中心处，随后向边界方向发展，加筋板进入塑性大变形(mode Ⅰ)的失效模式；加筋板受到第2次冲击后，失效模式仍表现为塑性大变形(mode Ⅰ)，残余挠度增加；加筋板受到第3次冲击后，局部的撕裂率先发生在加强筋所在的边界处，这是由于加筋板中心发生较大塑性变形，导致加筋板所在边界位置的拉伸应变率先达到了极限状态，发生了失效，失效模式由局部塑性大变形(mode Ⅰ)失效模式向局部边界处拉伸撕裂(mode Ⅱ)失效模式转化；加筋板受到第4次冲击，边界的撕裂会由加强筋所在的边界向两端延伸且伴随有加强筋撕裂的现象，随着冲击次数的增加，最终将会导致沿边界的完全撕裂失效，发生脱落。

图5 残余挠度云图

可见，Conwep算法和ALE算法都能够描述加筋板受多次冲击波作用的动态响应，并揭示不同次数冲击波作用下加筋板的失效模式及失效模式的转化历程。

3.2 板中心挠度分析

图6为采用不同算法的加筋板中心挠度随时间变化的历程曲线，加筋板的残余挠度随冲击次数的增加也逐步增加。在加筋板受到爆炸冲击后，能量由冲击波传入加筋板，并转化为加筋板的塑性变形能和动能，由于边界条件为完全固支，加筋板结构的动能具体表现为自由振动。由于在每次冲击后利用重启动添加阻尼的原因，加筋板的自由振动得到了很好的消除，最终进入稳定状态。加筋板受到第4次冲击后残余挠度产生了较大变化，这是因为第3次冲击后加筋板在边界上已经出现局部的撕裂，边界对加筋板的约束能力减弱。此外，随着冲击次数的增加，加筋板的损伤也在增加，导致其抵抗冲击的能力下降。最后，不同算法下加筋板的中心挠度变化趋势也具有一致性。

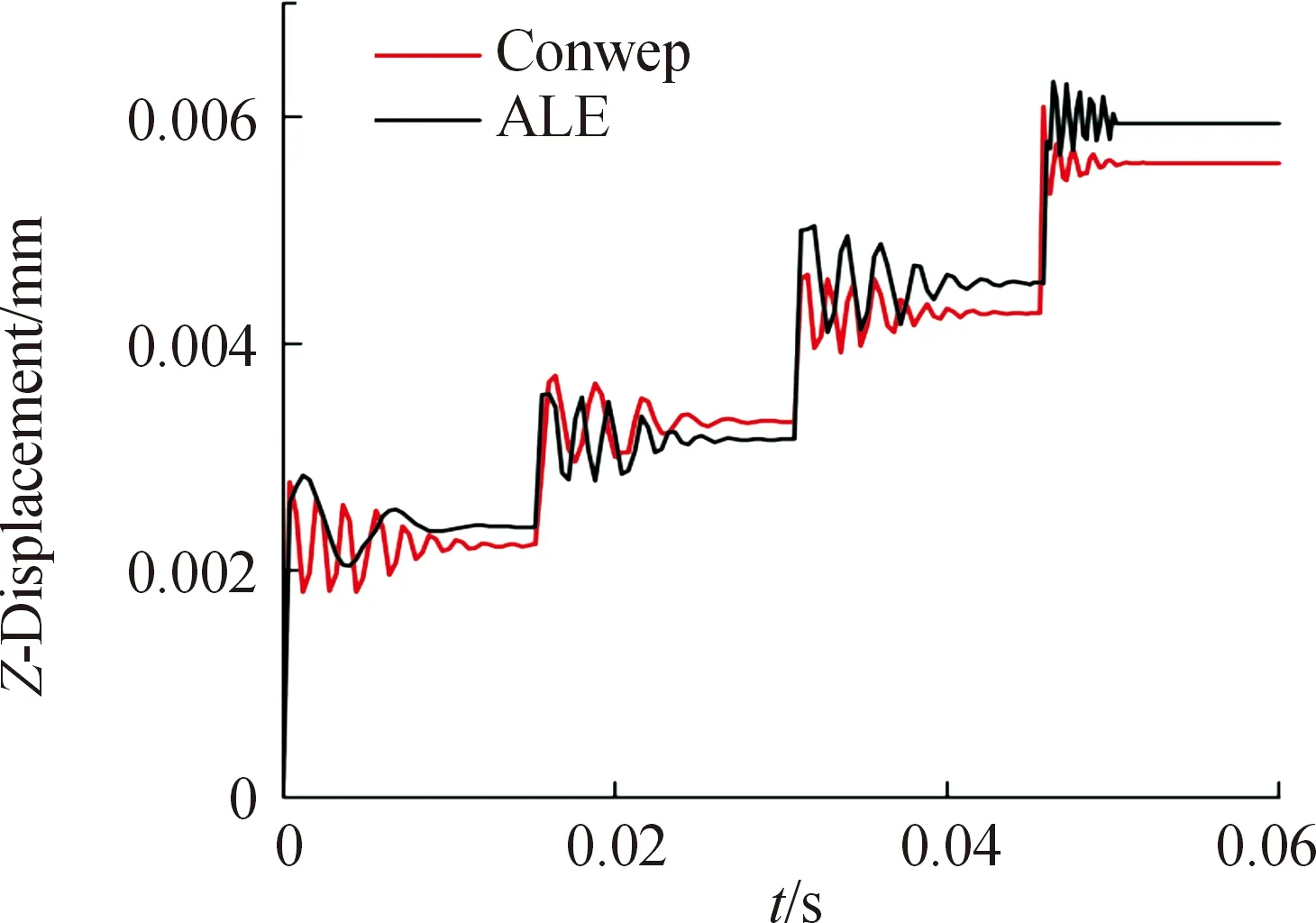
图6 加筋板Z方向位移时程曲线

提取不同算法下加筋板受冲击后稳定状态的最大残余挠度值，并计算相对误差，如表2所示。

表2 不同算法残余挠度对比表

相比于Conwep算法，ALE算法能够考虑复杂的流固耦合关系，将会导致相对误差的产生。此外，采用ALE算法时，因为流固耦合关系需利用关键字*CONSTRAINED_ LAGRANGE_ IN_SOLID定义，所以加筋板需采用Solid单元，而采用Conwep算法时，加筋板采用Shell单元，这将进一步导致误差的产生。但考虑到ALE算法及Conwep算法都能够揭示多次冲击波作用下加筋板不同的失效模式及失效模式的转化历程，且板中心挠度的变化具有相同的趋势，每次冲击后残余挠度的相对误差均小于10%，可认为2种算法都适用于加筋板多次冲击的数值模拟。相比于ALE算法，Conwep算法更为高效，更适用于本文中的大量计算，因此后续讨论采用Conwep算法进行模拟。

煤矿GIS“一张图”，是煤矿空间环境数据组织集成的统一框架，是2DGIS或2D+3DGIS一体化的服务平台，是基于统一地理信息平台的煤矿安全生产大数据集成和展示平台，其核心理念是“综合、集成”统一管理、“随时、随地”访问使用，“持续、及时”协同、动态更新，服务于技术、生产、安监、防灾应急等煤矿大数据分析展示等。

4 不同因素对加筋板动态响应的影响

本节将分别讨论在多次冲击波作用下加强筋的构型、边界条件对加筋板毁伤效应的影响。

4.1 加强筋构型的影响

图7为常见的加强筋构型：单条加强筋(S)、2条加强筋(D)、单十字加强筋(C)、双十字加强筋(DC)。炸药质量仍为120 g，爆距150 mm，进行4次爆炸冲击模拟。

图7 常见加筋板结构示意图

图8为不同结构形式的加筋板受4次爆炸冲击的残余挠度云图，不同结构形式的加筋板受到首次冲击后都进入塑性大变形(mode Ⅰ)的失效模式，最大残余挠度分别为3.19 mm(S)、2.73 mm(D)、2.46 mm(C)，可见在加强筋数量相同条件下，十字形构型的加筋板比单向构型的加筋板有着更好的抗爆性。不同构型加筋板受到第2次冲击后，单条加强筋的加筋板率先在加强筋所在边界处出现拉伸撕裂，撕裂总长度为20 mm，占全部边界尺寸的5.56%。其余构型的加筋板仍处于塑性大变形失效模式(modeI)，最大残余挠度为：4.03 mm(D)、3.88 mm(S)；受到第3次冲击后，所有构型的加筋板都进入局部撕裂的失效模式，总撕裂长度为：156 mm(S)、96 mm(D)、64 mm(C)，占全部边界尺寸的43.3%(S)、26.7%(D)、17.8%(C)。受到第4次冲击后，单条加强筋的加筋板发生边界的全部拉伸撕裂，其余构型加筋板拉伸撕裂的尺寸为：236 mm(D)、208 mm(C)，占全部边界尺寸的65.6%(D)、57.8%(C)。经过4次爆炸冲击载荷作用，所有构型的加筋板都已完成失效模式的转化，进入拉伸撕裂的失效模式(mode Ⅱ)。

图8 多次冲击下不同构型加筋板残余挠度云图

4.2 边界条件的影响

改变边界条件为四端简支和两端简支两端固支，研究边界条件的约束能力对双十字加筋板(DC)毁伤效应的影响。

图9为不同边界条件下加筋板受4次冲击后的残余挠度云图。当边界条件为四端简支时，加筋板没有在边界处出现大尺寸的拉伸撕裂，而是在第3次冲击后发生加强筋的断裂，在第4次冲击后面板中心处出现破口。这是因为边界约束的减弱使加筋板出现更大的残余挠度，板中心受拉伸程度大于边界处，所以率先引起加强筋的断裂。当边界条件为两端简支两端固支时，第3次冲击后边界的拉伸撕裂仅发生在固支边界上，这是因为固支边界具有更强的约束能力，在相同载荷条件下，边界处受拉伸产生的塑性应变更大，最终导致了拉伸撕裂的发生。