多轴数控系统在曲面加工中的应用

谭伟美 刘燕萍 凌海全

（广西玉林农业学校，广西 玉林 537000）

制造业的集成化水平、自动化水平，已经成为衡量一个国家科技实力的重要标准。我国是制造业大国，涵盖了世界上绝大多数的机械加工门类[1]，其中的数控技术和数控系统发挥了非常重要的作用。对各种复杂类型的机械加工任务，只有具备更多轴数联动的数控加工技术和方法，才能更高效率地将其完成[2]。因此，多轴联动数控系统的设计以及多轴联动的数控加工方法已经成为判断机械加工制造行业竞争力的核心内容[3]。目前，我国在5轴及5轴以上的联动数控系统研制和数控加工方法方面与世界先进水平存在一定差距，这也成为制约我国机械加工行业深度发展的瓶颈问题。为此，该文以5轴联动的数控系统为研究对象，通过数学模型分析和控制过程研究，给出其在曲面加工中的具体应用。

1 多轴数控系统位姿的数学模型

多轴联动的数控系统，其控制功能和加工效果实现的关键在于位置和姿态的准确刻画与合理动态连接。为此，该文先以齐次坐标的形式对多轴联动数控系统的位置和姿态进行数学建模。

多轴联动数控加工系统一系列动作的完成，在三维空间中表现为各个关节、各个轴的旋转运动和平移运动的累加效果。因此，要从数学角度刻画多轴联动数控系统，就依赖于对旋转矩阵和平移矩阵的刻画。

如果空间中任意一点A，通过平移变换变成A'点的位置，并且它在x、y、z这3个坐标轴上分别平移了a、b、c个单位，那么存在如公式（1）所示的平移关系。

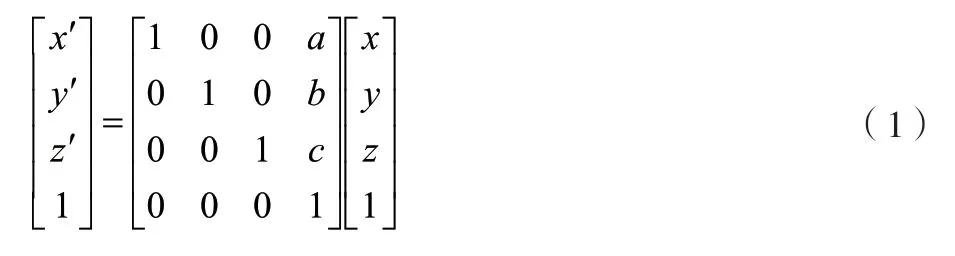
如果空间中任意一点A，通过旋转变换变成A'点的位置，并且它绕z旋转的角度为θ，那么存在如公式（2）所示的旋转关系。

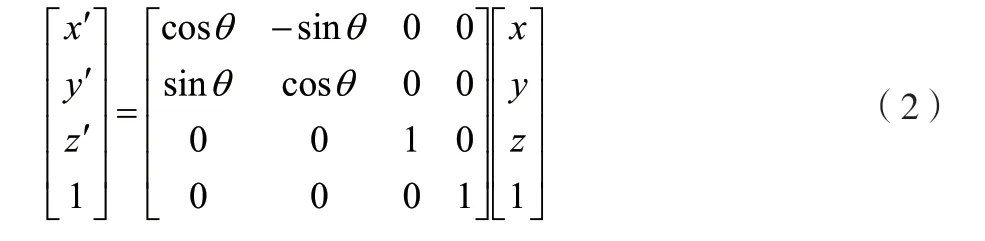
同理，还可分别得到任意一点绕y轴和绕x轴的旋转矩阵，以及这2个矩阵的齐次表达。进一步推广这个做法，可以得到任意一点绕空间任意轴线的旋转矩阵，它也将体现为绕x、y、z轴做旋转运动的组合形式。

得到了空间任意一点位置变化的平移矩阵和旋转矩阵，就可以建立这一点位置变化的数学模型。这样的思路同样适用于空间任意一个坐标系和空间任意一个物体。多轴联动的数控加工过程就是承担加工任务的操作端，进行多个平移运动和绕多个轴线做旋转运动的组合效果。

假设多轴联动系统的末端操作装置的位置变换如图1所示。

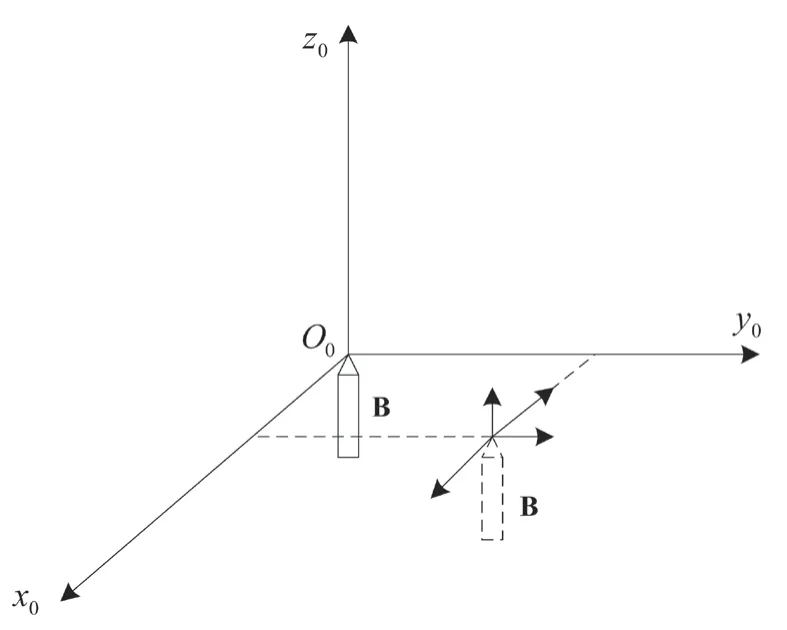
图1 多轴联动系统的末端操作装置的位置变换

如图1所示，多轴联动系统的末端操作装置一共进行了2次变换，一次是分别沿x轴和y轴进行了2次平移运动，一次是绕z轴做了90°的旋转。

可见，有了上面的建模方法，就可以对多轴联动系统任意关节、任意动作进行平移运动和旋转运动的组合描述。

2 多轴数控系统的加工过程控制

能够通过数学模型对多轴联动的数控系统进行描述以后，如何设定数控程序，让系统按照既定的路线完成加工任务，是整个数控过程的难点。该文为多轴联动数控系统的加工过程设计了一个具有较好实时性的脉冲控制算法，简称RTPA（Real time pulse algorithm）算法。

数控加工的过程一般是通过插补算法来实现和完成的，而数控加工中的每个轴的控制是根据步进电机的脉冲来实现的，这就需要形成插补过程和脉冲生成时序之间的对应关系。但是，传统的根据脉冲频率进行插补过程的设计的实时性并不理想。为此，该文从V-F变换算法（电压-频率）的角度出发，设计了一个新的具有更好实时性的脉冲生成算法。通过这个算法所产生的脉冲序列可实现对多轴联动数控系统更有效的控制。

这个算法使用了比较器组件、计数器组件和生成器组件共同产生具有较好实时性的脉冲序列，其算法的原理框图如图2所示。

根据图2可知，多轴联动系统某一关节或末端装置的位移经过采样以后作为RTPA算法的输入，采样频率是f。采样位移值输入以后，与反馈支路上根据脉冲计数器形成的脉冲当量进行比较，二者比较之后的差异进入脉冲生成器作为脉冲序列产生的判断依据。脉冲生成器会形成2个输出，分别是正向脉冲和反向脉冲，这也分别对应于步进电机的正转和反转。

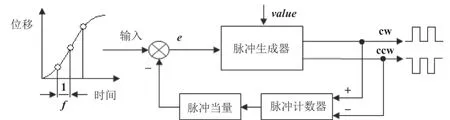
图2 多轴联动系统RTPA控制算法的原理框图

对脉冲生成器产生正向脉冲还是反向脉冲的判断，取决于输入与反馈支路比较的累积误差和设定域值（value）之间的比较，比较规则如下。规则一：如果输入与反馈支路比较的累积误差之和大于设定域值，则脉冲生成器生成正向脉冲并输出。规则二：如果输入与反馈支路比较的累积误差之和小于设定域值的相反数，则脉冲生成器生成反向脉冲并输出。

决定该文算法的关键参数还有位移作为输入前的采样频率f。为了判断采样频率f对RTPA算法性能的影响，该文分别设置采样频率为5 kHz和20 kHz，绘制其位移响应曲线和速度响应曲线，结果如图3所示。

图3（a）图左侧代表了采样频率为5kHz时RTPA算法的位移响应曲线，右侧代表了采样频率为20kHz时RTPA算法的位移响应曲线；图3（b）图左侧代表了采样频率为20kHz时RTPA算法的速度响应曲线，右侧代表了采样频率为20kHz时，RTPA算法的速度响应曲线。

从图3（a）可以看出，采样频率越大，采样周期越小，RTPA算法的位移响应速度越快。从左、右图的对比可以看出，采样频率为5kHz时，RTPA算法的位移响应经过0.58s，多轴联动系统的实际位移才能和理想位移吻合；采样频率为20kHz时，RTPA算法的位移响应经过0.16s，多轴联动系统的实际位移就和理想位移吻合。这表明，采样频率为20kHz时的位移响应比采样频率为5kHz时的位移响应足足快了0.42s。

从图3（b）可以看出，采样频率越大，采样周期越小，RTPA算法的速度曲线响应越快。从左、右图的对比可以看出，采样频率为5 kHz时，RTPA算法的速度响应经过0.5 s，多轴联动系统的实际速度才能和理想速度吻合；采样频率为20 kHz时，RTPA算法的速度响应经过0.13 s，多轴联动系统的实际速度就和理想速度吻合。这表明，采样频率为20 kHz时的速度响应比采样频率为5 kHz时的速度响应足足快了0.37 s。

3 多轴数控系统的曲面加工仿真试验

在前面的工作中，分别针对多轴联动数控系统进行了位置姿态建模和RTPA控制算法设计，并通过关键参数的影响分析确定了多轴联动数控系统的有效控制策略。接下来将进行仿真试验，以验证该文所提出的多轴联动系统的RTPA算法控制性能。

仿真试验选择曲面加工作为多轴联动数控系统的加工对象。曲面在各种加工单元中具有一定的复杂性，并且对控制算法有比较精细的要求。而整个曲面的加工完成是通过连续的曲线加工轨迹来完成的。该文要加工的曲面的仿真结果如图4所示。

从图4可以看出，该文要加工的曲面是在x方向上形成轴向宽度、在y方向上形成径向宽度的一段曲面，曲面的曲率半径则位于z轴方向。图4中还给出了刀具的初始位置即起刀点，曲面上的平行曲线则表明在RTPA算法控制下的加工轨迹。

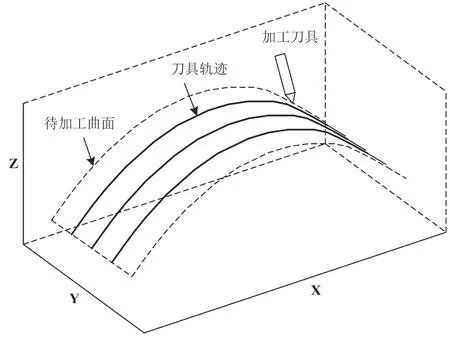
图4 该文要加工的曲面的仿真结果

曲面的数控加工方法有很多种，例如基于轨迹生成参数的加工路线法、基于CC路径的截面数据加工路线法以及基于CL路径的截面加工路线法等。该文选择了基于CC路径的截面数据加工路线法，同时结合Z字形走刀完成加工。

加工过程中，RTPA算法在x轴方向上、y轴方向上和z轴方向上，根据RTPA算法得到的位移和速度曲线的控制效果如图5所示。

从图5（a）中可以看出，RTPA算法在x轴方向上对位移的控制形成了三角波的曲线形式。受到加工任务的限制，RTPA算法在x轴方向上的位移最大值为0 mm，最小值接近-150 mm的位置，位移曲线的三角波周期4.17 s。RTPA算法在x轴方向上对速度的控制形成了矩形方波的曲线形式，但因为加工过程的影响出现了一定的抖动。RTPA算法在x轴方向上的速度最大值接近80 mm/s，最小值接近-80 mm/s，速度曲线的矩形方波周期4.17 s。

从图5（b）中可以看出，RTPA算法在y轴方向上对位移的控制形成了阶跃波的曲线形式。受到加工任务的限制，RTPA算法在y轴方向上的位移最大值为0 mm，最小值接近-6 mm的位置，位移曲线的阶跃波周期4.17 s。RTPA算法在y轴方向上对速度的控制形成了脉冲波的形式。RTPA算法在y轴方向上的速度最大值为0 mm/s，最小值为-10 mm/s，速度曲线的矩形方波周期4.17 s。

从图5（c）中可以看出，RTPA算法在z轴方向上对位移的控制形成了正弦半波的曲线形式。受到加工任务的限制，RTPA算法在z轴方向上的位移最大值为6.2 mm，最小值为0 mm的位置，位移曲线的正弦半波周期2.08 s。RTPA算法在z轴方向上对速度的控制形成了锯齿波的曲线形式。RTPA算法在z轴方向上的速度最大值接近15 mm/s，最小值接近-15 mm/s，速度曲线的锯齿波周期2.08 s。

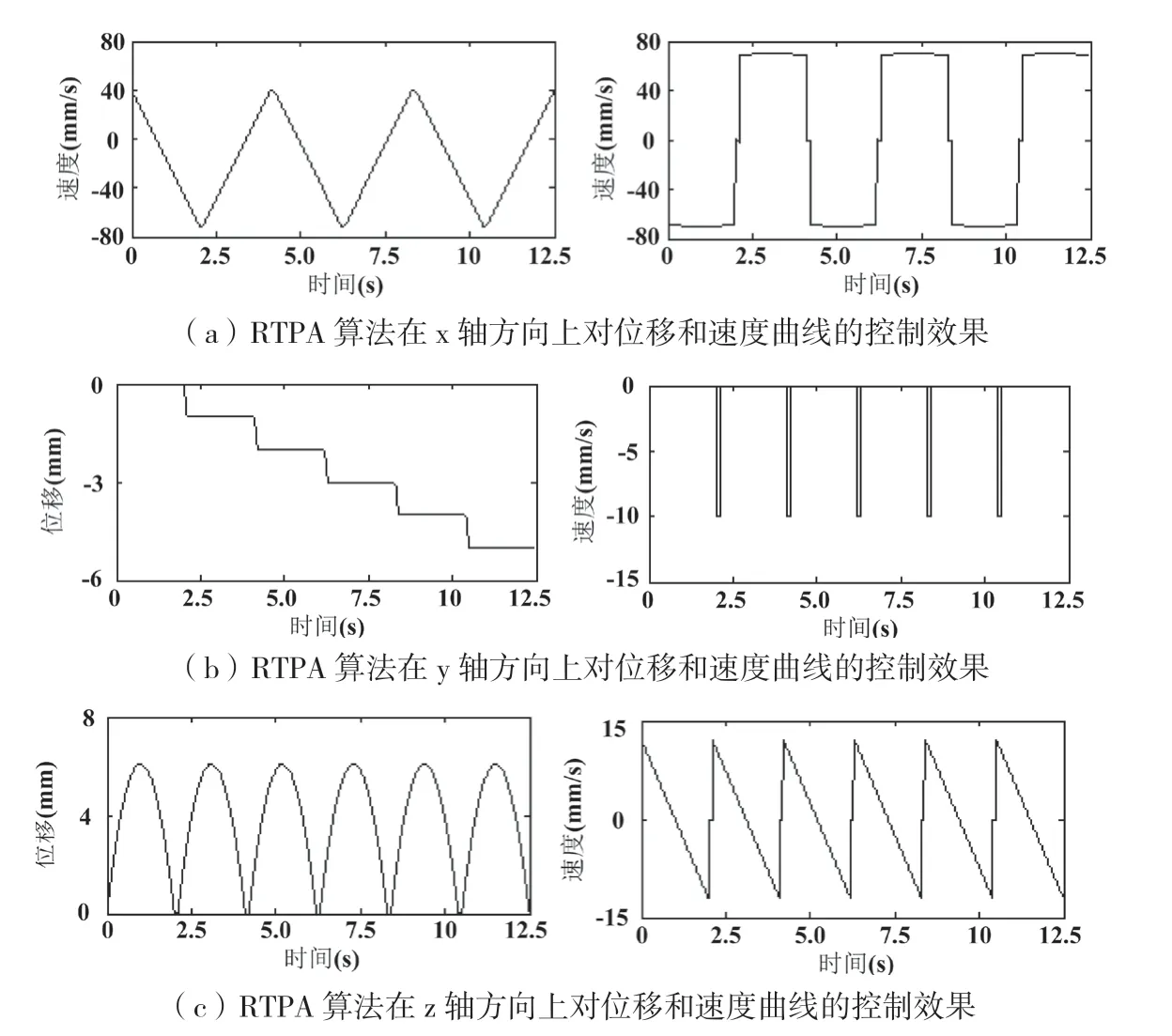
图5 RTPA算法在3个方向上对位移和速度曲线的控制效果

4 结论

该文对多轴联动的数控系统进行了研究。首先，在齐次坐标的形式下，对多轴联动系统任意关节处的位置和姿态变化进行数学建模，推导了平移矩阵和旋转矩阵的产生过程。其次，基于比较器组件、计数器组件和生成器组件构建了反馈形式的RTPA算法，用于多轴联动数控系统加工过程中的实际控制，并对采样频率的影响进行了分析。最后，以曲面仿真加工为例进行了验证性试验，试验结果表明：该文采用的基于CC路径的截面数据加工路线法，同时结合Z字形走刀可以顺利完成加工。同时，RTPA算法在3个坐标轴方向上对位移和速度都进行了有效的控制。