基于不平衡数据与集成学习算法的信用评价模型
2022-12-13王灿
王 灿
(上海邮电设计咨询研究院有限公司,上海 200093)
0 引言
个人信用实际是借款人与金融机构或出资方的隐形契约,能降低交易行为的成本[1]。但是当信贷交易完成后,借款人未按期履约,将给贷款机构造成损失。美国次贷金融危机以及国内2018年以来多起P2P平台“暴雷事件”,导致国内外对个人信贷业务的开展越发慎重。为了降低信用风险,一套有效的个人信用评价体系及方法显得尤为重要[2]。
与西方发达国家相比,我国个人信用评价体系、技术起步较晚,传统人工经验打分法已无法满足迅猛发展的信贷业务。中办国办印发《关于推进社会信用体系建设高质量发展促进形成新发展格局的意见》(2022)指出:支持金融、征信和评级等机构运用大数据等技术加强跟踪监测预警。同时,在业界和学术界,构建既符合信贷业务特点又高效可行的机器学习方法逐渐成为热门研究课题。
该文以个人贷款业务为背景,将信用风险评估抽象为监督学习下2类分类问题,采用EasyEnsemble方法解决个人信用数据普遍存在的数据不平衡问题,对多种单一模型集成进行模型融合,采用准确率、召回率等指标对模型进行评价,以验证集成学习方法的有效性。
1 不平衡数据处理
1.1 数据不平衡问题分析
对监督学习下的2类分类问题来说,当2种类别样本数量差别较大时,被称为“数据不平衡”,即某一类样本数远小于另一类样本数,可能会导致分类边界受多数类样本的影响[3]。
实际上,银行、信贷机构多数类数据样本是非逾期客户的信息,而逾期客户占比大约为10%,存在严重的正负样本不平衡问题,例如在一个信用数据集中,多数类(非逾期)样本有90个,少数类(逾期)样本只有10个,将所有样本都归为非逾期,识别准确度可达到90%,这时,准确率虽然高,但是对贷款业务来说,其结果的意义不大。当面对数据集不平衡时,以SVM、LR等为代表的机器学习方法仅能得到次优结果。
1.2 数据不平衡处理
目前,有2个主流方法可以处理数据集不平衡问题,即抽样技术和代价敏感学习[4]。其中,抽样技术可利用欠采样方式进行数据重构,使数据分类能达到平衡,即选择少量的多数类样本与少数类样本构成新的训练集,这种方法虽然使样本整体比例均衡,但是该方法会使样本数减少,导致信息缺失,让某些特征不能较好地显现,最终使分类模型欠拟合。
为了避免欠拟合技术的缺陷,该文采用EasyEnsemble方法对不平衡数据进行处理,该算法类似于随机森林(Random Forest, RF)的Bagging方法。首先,将数据集划分为多数类和少数类2个部分。其次,对多数类样本进行不放回抽样,经过n次操作后,生成n份子集。再次,将n份样本子集分别与少数类样本合并训练一个模型。最后,可以得到n个模型,以n个模型预测结果的平均值作为最终模型。进行EasyEnsemble处理后,如果每组多数类与少数类样本比值约为3∶1,根据文献[5]可知,该比例适合进行数据集训练。
2 分类器的集成
2.1 Bagging主要思想
集成学习方法是机器学习领域的一个分支,具有一定的理论体系,主要思想为通过一定手段,训练得到多种单一学习模型(基分类器),要求这些基分类器为弱分类器(误差率小于0.5),然后,将多种基分类器进行排列组合,通过融合输出结果来形成分类边界,该分类结果往往比单一学习模型预测结果更好,即融合后的分类边界将更接近真实边界。
常见框架有Bagging模型和Boosting模型,简单来说,这2种方法就是通过“并联”或“串联”的结构将基分类器进行组合,并按照一定规则对最后的结果进行融合,旨在提高模型的稳定性或预测精度。其中,Bagging(Bootstrap Aggregating)由Breiman(1996)提出,主要按一定比例对训练集进行重采样,然后构成不同的分类器,最后再按一定规则对结果进行融合。
为了充分利用信用数据,增强模型泛化能力,该文采用无放回的方式随机抽取训练数据,然后对不同分类器进行集成,包括SVM、LR回归、DT以及k-NN等,最终的分类(或回归)结果是n个单独分类器分类结果的“多数投票”。
2.2 集成模型
该文以4种弱分类器为基分类器,分别是非对称误差成本的核支持向量机(Support Vector Machine,SVM)、逻辑斯蒂回归(Logistic Regression, LR)、C5.0算法的决策树(Decision Tree, DT)以及带有距离加权的k-NN算法(k-Nearest Neighbor,k-NN)。
非对称误差成本的核SVM是在普通SVM模型基础上,通过某些核函数转化提高模型处理非线性问题的能力,该文采用径向基核。同时,考虑信用评价时将逾期误判为非逾期和将非逾期误判为逾期的2种错误分类的成本不同,因此在径向基核SVM的基础上,再引入非对称误差成本,即增加将高风险样本误判为低风险样本的成本。这样虽然降低了分类准确率,但是更符合信贷业务的实际情况。
逻辑斯蒂回归是一种经典的机器学习模型,常用于解决监督学习下的二分类问题,LR模型是在普通线性回归模型基础上引入Sigmoid函数,将线性回归模型产生的数值带入Sigmoid函数,最后输出[0, 1]的结果,以代表对应样本二分类概率。对信贷业务来说,该结果能反映样本的违约概率,因此LR模型及其优化被广泛应用于信贷业务。
C5.0算法的决策树是一种经典的分类方法,C5.0是其常见算法,主要是以信息熵的下降速度作为节点分裂准则来构建整个决策树。同时,为了降低模型过拟合风险,对决策树进行剪枝,该文采用悲观剪枝法,其使用统计置信区间的估计方法,在估计得到误差后,C5.0算法以“减少误差”为依据判断是否剪枝。
带有距离加权的k-NN算法是一般k近邻法算法的改进,k近邻法是通过计算距离得到的,新样本与原数据集最近距离的k个样本,将新样本归集到k个样本中的多数类。但在分类时,某一类样本量远大于其他类别,该算法容易出现误判。为了降低这一类误判的风险,该文在计算欧式距离时,加入距离权重,对离新样本距离更近的数据点赋予更高的权重,以减少数据不平衡对k-NN算法的影响。
对数据集进行基分类器训练,采用不放回Bagging方法,将以上弱分类器以“并联”的方式集成(图1),并在调试参数过程中,给在集成模型中表现较好的分类器赋予更高的权重。其中,每个分类器的参数设置都不相同,形成异构基分类器,保证各单独分类器的分类准确率及召回率的表现不同。因此,该模型将进一步提高表现较好的分类器在集成模型中的权重,使其在投票阶段占比更高,对最终结果影响更显著。
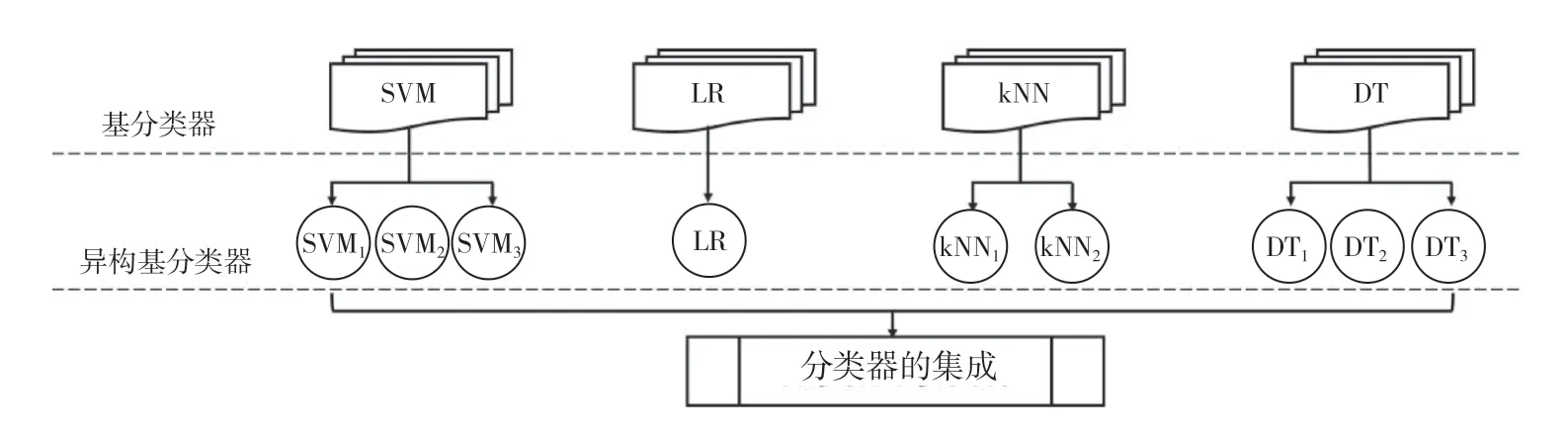
图1 集成分类器示意图
3 实证研究
该文使用某贷款机构提供30 000个贷款报告信息,所有数据来源于某贷款机构经一定处理的数据(非原始数据),使用Python 2.7.12进行求解和检验。
3.1 数据描述与预处理
该文有30 000样本,原有19项具体特征指标。由传统“5C”原则[6]划分指标的中间层,再由6项基本原则[7]确定中间层展开(图2),经多重共线性及显著性检验后,最终选取16个特征指标,包括是否本地籍、教育程度、婚姻情况、收入、贷款逾期笔数、贷款逾期月份数、贷款单月最高逾期总额、贷款最大贷款时长、贷记卡以及准贷记卡相关项等指标,以上16项指标能反映个人自然状况、经济状况和信用情况。
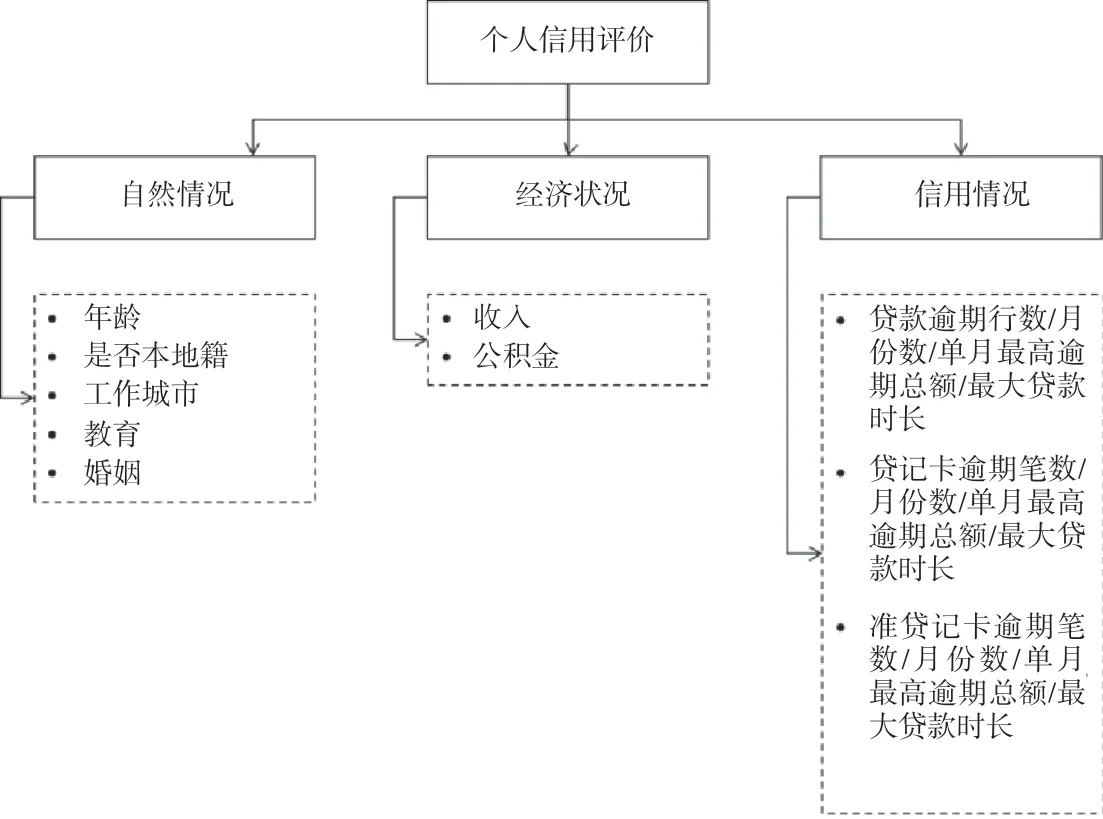
图2 信用评价指标体系图
对16项指标进行数据转换,以便进行后续处理及模型训练。其中,对是否本地籍指标来说,一般本地户籍样本违约成本较高,违约概率较低,对该特征采用布尔值,0表示非本地户籍,1表示本地户籍。对教育程度指标来说,文化程度高的群体信用意识强,违约风险相对较低,对该特性进行离散化处理,依次用1~8表示初中至博士研究生。对婚姻情况指标来说,婚姻状况反映样本所受家庭或社会关系约束的程度,已婚人士违约机会成本高于未婚人士,其违约概率较低,对该特性进行one hot编码处理,即对已婚、未婚以及离异(单身)等状态进行编码。其他指标(例如收入、贷款逾期笔数等)无需转换。
在30 000个样本中,非逾期与逾期数据比达到15∶1,见表1。存在数据不平衡问题,采用EasyEnsemble方法,对30 000个样本进行集成欠采样,将多数类样本(非逾期类)随机不放回地分为5组,再将这5组与少数类(逾期类)进行合并,经过该处理后,每组多数类与少数类样本比值约3∶1,生成易于后续模型学习训练的数据集。

表1 原始数据集基本情况
同时,为了避免EasyEnsemble后,单组数据集样本量减少,增加模型泛化能力,该文运用交叉验证方法(Cross validation)将数据集随机划分为k等份(k-折交叉验证),即将原有训练集随机拆分为k个大小基本相等且互不重叠的区域,选取其中k-1份作为训练模型,剩下1份作为测试集。这样,将进行k次模型训练,通过k个不同结果计算准确率、召回率以及AUC值等平均值,以调整模型合适的参数。根据经验法则,将k值设置为10,该文采用10-折交叉验证进行模型训练与调参。
3.2 数据集求解与检验
将5组欠采样处理后的数据进行10-折交叉验证,依次将这50组数据集代入SVM分类器、LR分类器、k-NN分类器以及DT分类器进行交叉验证。在信用分类器性能评价时,求取准确率和召回率的平均值,将其作为效果评价指标。各分类器求解及验证结果见表2~表5。
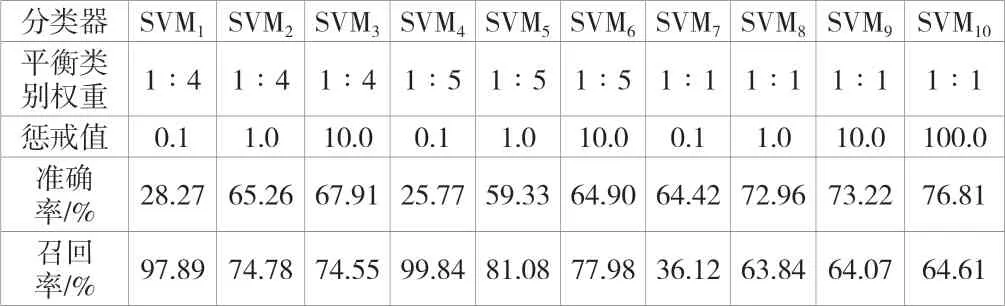
表2 SVM 分类器参数设置及模型验证
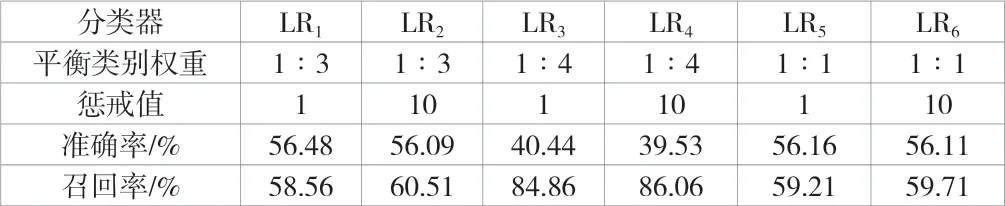
表3 LR分类器参数设置及模型验证

表4 DT分类器参数设置及模型验证
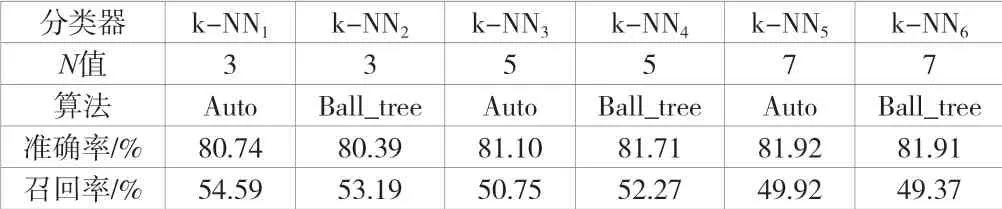
表5 k-NN分类器参数设置及模型验证
单个分类器训练学习完毕后,通过并行Bagging集成的方法完成最终集成模型,集成分类器的模型检验结果见表6。由表6可知,集成后的准确率达到73.94%,召回率达到81.21%,其结果整体优于单个分类器的分类效果。同时,模型检验结果较差的是LR分类器。
在对每个分类器进行参数优化后,通过集成算法将弱分类器组合在一起,以增加模型的稳定性和鲁棒性,然而不同的分类器组合带来的分类效果也不相同,该文分别对比了三分类器组合、五分类器组合、七分类器组合及九分类器组合,得出各AUC(Area Under Curve,受试者工作特征曲线下面积)值,见表7。经比较,九分类器(表6中9个单一分类器)的组合效果为最好。

表6 集成分类器模型验证

表7 AUC值
4 结语
该文根据个人信用数据的特点,引入EasyEnsemble方法进行多数类与少数类数据比例平衡,并基于集成学习方法提出了一种可通用于个人信用评价的集成学习算法,对Bagging主要思想进行统一和推广。在一定程度上解决了信用评价的2个问题(数据不平衡和对少数类(逾期类)的识别),旨在识别逾期风险较大的借款人,以降低信用风险。
在实例分析时,以某贷款公司个人贷款业务为背景,依次完成信用指标体系构建、原始数据处理以及模型选取等工作。其中,针对信用数据不平衡的问题,在运用EasyEnsemble方法后,每组多数类与少数类样本比值由15∶1降为3∶1,再以SVM模型、Logistic回归、k-NN算法以及DT模型进行并行集成,通过九分类器组合得到最终模型,与单一分类器相比,集成分类器可以提高逾期样本的识别效果。
