基于改进差分进化算法的Ⅱ型频率采样法FIR数字滤波器设计

胡仕兵, 聂 喜, 陈子为

(成都信息工程大学电子工程学院,四川 成都 610225)

0 引言

频率采样法是设计FIR数字滤波器的常用方法之一[1-2],分为Ⅰ型和Ⅱ型两种,对应的滤波器频率响应Hd(ejω)的 N 点采样值分别为和。对Ⅰ型频率采样法应用和研究较广泛,而对Ⅱ型频率采样法很少述及。实际上在对FIR滤波器频率响应拟合程度要求较高的场合,可以将Ⅰ型频率采样法和Ⅱ型频率采样法交替使用,以获得更精准的边界频率,两种采样法的边界频率拟合误差曲线如图1所示。

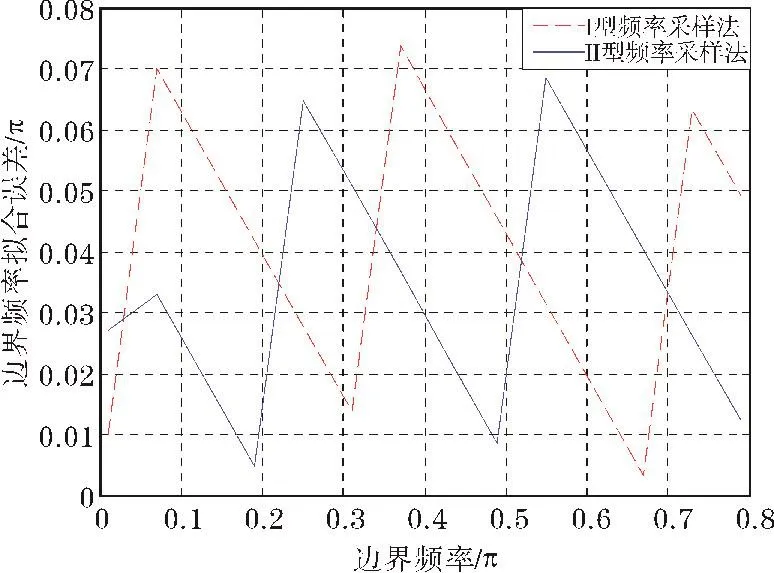
图1 Ⅰ型和Ⅱ型频率采样法FIR低通滤波器边界频率拟合误差曲线(过渡带宽0.15 π、过渡带内1个样点)

在确定FIR数字滤波器的过渡带样点值时,采用了查表(look-up table,LUT)法[3]、遗传算法(genetic algorithm,GA)[4-7]、模拟退火算法(simulated annealing algorithm,SAA)[8]、蚁群优化算法(ant colony optimization algorithm,ACOA)[9]、粒子群优化算法(particle swarm optimization algorithm,PSOA)[5,10-12]、免疫算法(immune algorithm,IA)[13]、克隆选择算法(clonal selection algorithm,CSA)[14-15]、自由搜索算法(free search algorithm,FSA)[16]、水循环算法(water cycle algorithm,WCA)[17]、人工鱼群算法(artificial fish swarm algorithm,AFSA)[18]等,这些方法在一定程度上存在求得最优解的偏差过大、算法群体多样性较小、算法控制变量多、结构较复杂、寻优精度不高、收敛速度较慢、易于出现早熟收敛(易陷入局部最优解)和程序运行时间较长等缺陷。差分进化(differential evolution,DE)算法是由Rainer Storn等[19-21]于20世纪末提出的一种基于模拟自然界生物的进化过程、求解连续空间上优化问题的高效、强大的随机种群搜索算法,由于其控制参数少、计算简单、易于实现等特点,引起广泛关注和研究。但是对于特定的优化问题,DE算法也表现出对控制参数的设置敏感、收敛速度慢、种群搜索停滞和早熟收敛等问题[21]。本文对DE算法进行改进,增加缩放因子自适应生成策略、交叉概率抛物线式动态产生策略和基因边界检查和处理方法,提出一种新的改进差分进化(modified differential evolution,MDE)算法并且应用于采用Ⅱ型频率采样法设计FIR数字滤波器时过渡带样点值的优化中,取得了良好的实验效果。

1 MDE算法

对于待优化的问题函数f,寻找参数x1,x2,…,xD使f达到最小值:

其中:D是解空间的维数,Uj和Lj分别是第j个分量xj取值范围的上界值和下界值。MDE算法包括4个基本操作:初始化种群、变异、交叉和选择。在初始化种群后,算法循环执行变异、交叉和选择操作,直到计算结果在预期的误差精度内或达到最大进化代数;最后获得最优解。

1.1 种群初始化

设进化代数为 G∈{0,1,…,Gmax}时的种群为P(G)={X1(G),X2(G),…,XM(G)},其中:M为种群规模大小,Xi(G)={xi,1(G),xi,2(G),…,xi,D(G)}(i=1,2,…,M)表示第G代中的第i个个体(染色体),xi,j(G)表示第 G代中第 i个个体的第 j个分量(基因)。每个个体代表解空间内的某一个解,而基因代表解的各个分量。种群初始化就是在解空间范围内随机均匀地产生M个个体,每个个体由D维向量组成,取值方式如下:

其中,rand(0,1)表示在(0,1)区间均匀分布的随机数。

1.2 变异运算

传统差分进化算法通过差分策略实现个体变异。对于每个个体Xi(G),从种群中随机选择3个不同的个体 Xp1(G)、Xp2(G)和 Xp3(G)(i≠p1≠p2≠p3)生成变异向量Hi(G+1):

其中:F∈[0,2]为缩放因子(常数),用于控制差分向量Xp2(G)-Xp3(G)的影响力。

F值较大时能使算法在全局范围内搜索到有效解,但会降低收敛速度;F值较小时会降低种群的多样性,导致陷入局部最优解,收敛性能差。本文提出改进方法:将Xp1(G)、Xp2(G)、Xp3(G)按照适应度值优劣进行排序得到个体向量Xbest(G)、Xmiddle(G)和Xworst(G),且有为计算个体适应度值函数,采用以下的自适应调整策略生成变异向量Hi(G+1):Fi的取值根据生成差分向量的两个个体适应度值作自适应变化。式(5)中,FL和FU分别是缩放因子的下限和上限,取FL=0.1,FU=0.9。自适应变异可以加快算法的收敛速度,避免有时陷入局部最优点的缺陷。

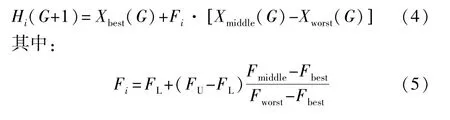
1.3 交叉运算

引入交叉运算可以增强种群的多样性。对于每个目标个体Xi(G)及其生成的变异个体Hi(G+1)进行个体间的交叉操作生成实验向量Vi(G+1),即按照一定的概率CR选择Hi(G+1)或Xi(G)的等位基因作为Vi(G+1)的等位基因。为保证变异中间体{Hi(G+1)}的每个染色体至少有一个基因遗传给下一代,需要随机取出Hi(G+1)中的第jrand位基因作为Vi(G+1)的第jrand位等位基因。Vi(G+1)的基因计算方式如下:

其中:CR∈[0,1]为交叉概率(常数),jrand为{1,2,…,D}间的随机整数。

常数CR值较大时,试验个体中的信息大多来自于变异个体,使种群的多样性越来越好,但容易忽略掉全局最优解,算法容易出现早熟收敛现象;CR值较小时,试验个体中的信息大多来自目标个体,会使种群性降低,导致种群进化出现停滞现象。故提出如下抛物线式动态CR策略:

其中,CR(G)为第G代的交叉概率,CRU和CRL分别是交叉概率的上限值和下限值,一般取CRU=1.0、CRL=0.9。这样CR在0.9处缓慢增长,可以减小固定参数带来的不足。

1.4 选择运算

采用贪婪算法从实验向量Vi(G+1)和原向量Xi(G)中选择出适应度值更高的个体作为下一代种群的个体,计算方式为

选择操作保证了个体Xi(G+1)一定优于或持平于Xi(G),使算法最终一定会收敛到某个最优点(可能是局部最优)上;而变异、交叉操作有助于解跳出局部最优达到全局最优。

1.5 边界检查和处理

为确保在进化过程中解的有效性,必须判断染色体中各基因是否超出边界,如果超出,则基因用随机方法重新生成或取边界值。假设是经过变异或者交叉操作后所得某个新个体的第j个基因,边界检查和处理算法为

2 Ⅱ型频率采样法设计FIR数字滤波器的原理

设待设计的理想滤波器频率特性为Hd(ejω),对其在ω的一个周期[0,2π)等间隔地抽样N个点(第一个抽样点在ω=π/N处),得

以上便是Ⅱ型频率采样设计法的原理,H(ejω)即为设计出的滤波器频率响应。

3 线性相位FIR数字滤波器的Ⅱ型频率采样设计公式

FIR数字滤波器具有线性相位的约束条件是h(n)是实序列且满足h(n)=±h(N-1-n)。将Hd(ejω)表示成幅度函数Hdg(ω)(可正可负的实函数)和相位函数θ(ω)的形式,即 Hd(ejω)=Hdg(ω)ejθ(ω)。 从而有

将式(18)和式(19)分别代入式(13)中,经化简后得频率响应H(ejω)的表示式为

与理想频响 Hd(ejω)严格相等;在抽样点之间,H(ejω)为 Hd(k)的加权内插函数的延伸叠加;Hd(ejω)变化越平缓,内插越接近理想值,逼近误差越小。图2的仿真曲线证实了这一结论,其中Hg(ω)是实际滤波器频响函数H(ejω)去掉相位特性后的幅度响应函数。通常设计出的滤波器的通带最大波动Rp为1.2 dB左右,阻带最小衰减As为18 dB左右,不能满足一般工程上的要求[1-2];可以在滤波器过渡带内增加一些样点,以达到提高阻带最小衰减As和减小通带最大波动Rp的目的。本文就是采用MDE优化算法寻找出这些样点的最佳值。

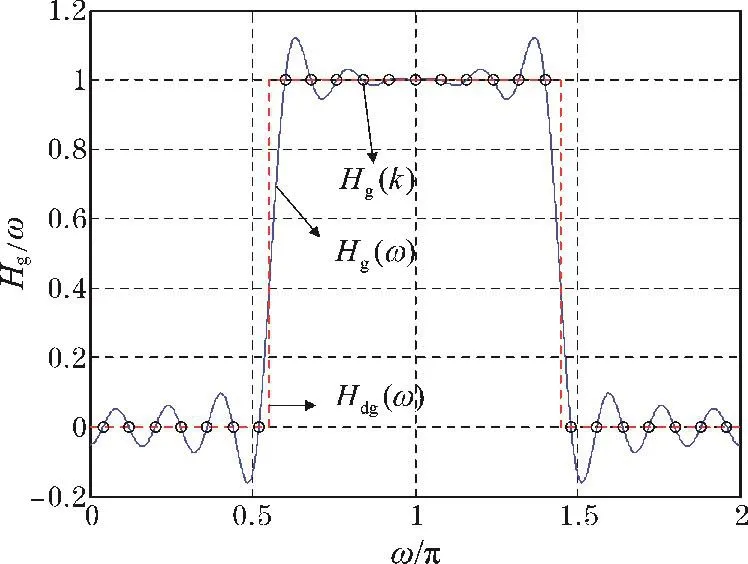
图2 Ⅱ型频率抽样法设计的FIR高通数字滤波器幅度响应(N=25、ωp=0.55π)

4 实验与结果分析

4.1 FIR高通数字滤波器设计实验

用Ⅱ型频率采样法设计一个第一类线性相位FIR高通数字滤波器,要求理想频率响应为陡变矩形,通带截止频率ωp=0.43π,阻带最小衰减As≥40 dB,过渡带宽度Δω≤0.08π。

解:由于要求As≥40 dB,确定滤波器过渡带样点数为m=1。FIR滤波器长度为N≥2π(m+1)/Δω=50,因为设计的是高通滤波器,N必须为奇数,取N=51。通带范围 k的取值为「ωpN/(2π)-1/2」≤k≤N-1-「ωpN/(2π)-1/2」(表示对 d朝+∞方向取最小整数),即11≤k≤39,故过渡带的样点值D1在k=10、40处,全部频率响应的样点值如下:

本文以获得最大的滤波器阻带最小衰减值为优化目标,因此计算个体适应度值函数为

其中:DFT(·)和IDFT(·)分别为离散傅里叶变换和离散傅里叶逆变换运算,为节省计算时间,采用快速的FFT和IFFT算法。为了只保留滤波器频谱函数中幅度特性部分,式中乘以以抵消相位特性信息,min(·)为取最小值运算。

在安装有Windows10 64位操作系统的Intel(R)Celeron(R)N3350@1.10 GHz CPU、4.00GB RAM 的PC机上用MATLAB7.0编写程序实现本例的MDE算法。其中算法参数设置为:种群规模大小M=250,解空间维数为D=1,寻优范围上界值U1=1和下界值L1=0,最大进化代数Gmax=100。实验结果如图3和图4所示,可见采用LUT法和MDE算法设计的FIR高通滤波器都达到了设计指标,但LUT法设计的滤波器通带最大波动值(0.5202 dB)大于MDE算法(0.4721 dB),且阻带最小衰减值(40.1331 dB)比MDE算法(43.0613 dB)小,所以MDE算法效果优越。该例MDE算法在经过22代的进化搜索后获得最佳解D1=0.38324,对应的适应度值为1.4226×102;程序运行的平均时间(取10次运行的平均值)为53.3141秒。

图3 Ⅱ型频率抽样法设计的FIR高通数字滤波器幅频响应曲线(N=51、ωp=0.43π、D=1)

图4 设计FIR高通数字滤波器时MDE算法适应度进化曲线

4.2 FIR低通数字滤波器设计实验

利用Ⅱ型频率采样法设计一个第一类线性相位FIR低通滤波器,理想通带截止频率ωp=0.35π,允许过渡带宽Δω=0.12π,阻带最小衰减As=60 dB。

解:因为阻带最小衰减As=60 dB,过渡带样点数取为m=2,FIR滤波器长度为N=2π(m+1)/Δω=50。通带范围0～ωp相当于k的范围为0≤k≤表示对 d 朝 0 方向取最大整数),即0≤k≤8,故过渡带的抽样值D1、D2应分别选在k=9、40和k=10、39处,写出频率响应的抽样点值为

在用MATLAB7.0编程实现该算法时,计算个体适应度值函数与式(23)相同,只是min函数操作的对象是设计出滤波器幅度函数Hg(ω)的前512个样点值(因为第一类线性相位FIR数字滤波器在单位脉冲响应长度N为偶数时,Hg(ω)关于ω=π奇对称);算法参数与4.1节完全相同,不同的是解空间维数D=2,寻优范围上界值U1,2=1,下界值L1,2=0。实验结果如图5和图6所示,可见MDE算法设计出的FIR低通滤波器通带最大波动值(0.3006 dB)小于LUT法(0.3603 dB),阻带最小衰减值(73.7692 dB)比LUT法(59.8452 dB)大得多,并且LUT法设计的滤波器阻带最小衰减值没有达到设计指标,因而MDE算法效果明显优于传统LUT法。该例MDE算法在经过77代的进化搜索后获得最佳解 D1=0.54297、D2=0.084864,对应的适应度值为4.88139×103;程序的平均运行时间为52.8375秒。

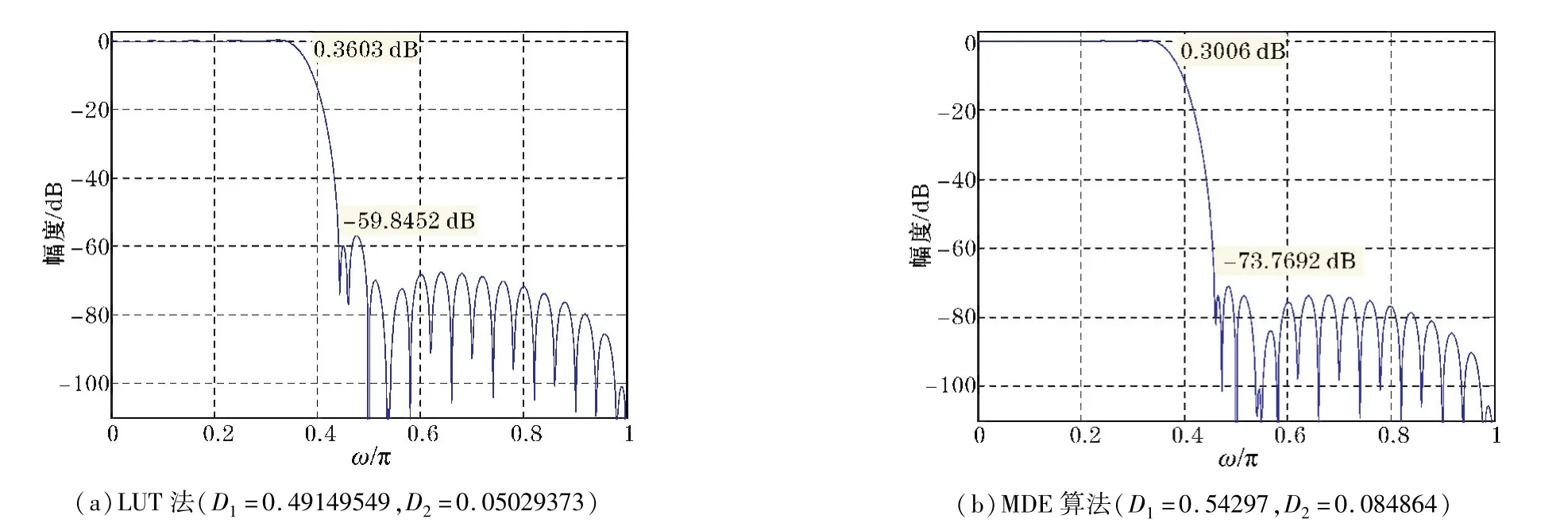
图5 Ⅱ型频率抽样法设计的FIR低通数字滤波器幅频响应曲线(N=50、ωp=0.35π、D=2)

图6 设计FIR低通数字滤波器时MDE算法适应度进化曲线

4.3 FIR带通数字滤波器设计实验

试利用Ⅱ型频率采样法设计一个理想频率响应为矩形的线性相位FIR带通滤波器,技术指标为:通带下边界频率和上边界频率分别为 ωp1=0.35π和 ωp2=0.7π,阻带下边界频率和上边界频率分别为 ωs1=0.25π和 ωs2=0.8π,通带波纹 Rp=0.5 dB,阻带最小衰减 As≥60 dB。

解:需要过渡带抽样点数为m=2,过渡带宽度Δω=ωp1-ωs1=ωs2-ωp2=0.1π,于是滤波器的长度点数为 N≥2π(m+1)/Δω=60,取 N=60,各边界频率的抽样点值 k分别为:。故过渡带抽样值D1、D2应分别位于 k=8、22、37、51 和 k=9、21、38、50处,于是有

在用MATLAB7.0编程实现时,算法参数以及计算个体适应度值函数与4.2节完全相同。实验结果如图7和图8所示,由结果可以看出:采用MDE算法优化设计的FIR带通滤波器通带最大波动Rp和阻带最小衰减As均满足设计要求,且具有比传统LUT法更好的幅频响应性能,即滤波器的通带波动较小、阻带衰减更大。该例MDE算法在经过52代的进化搜索后获得最佳解D1=0.11173、D2=0.59742,对应的适应度值为1.21487×103;程序的平均运行时间为54.1125秒。

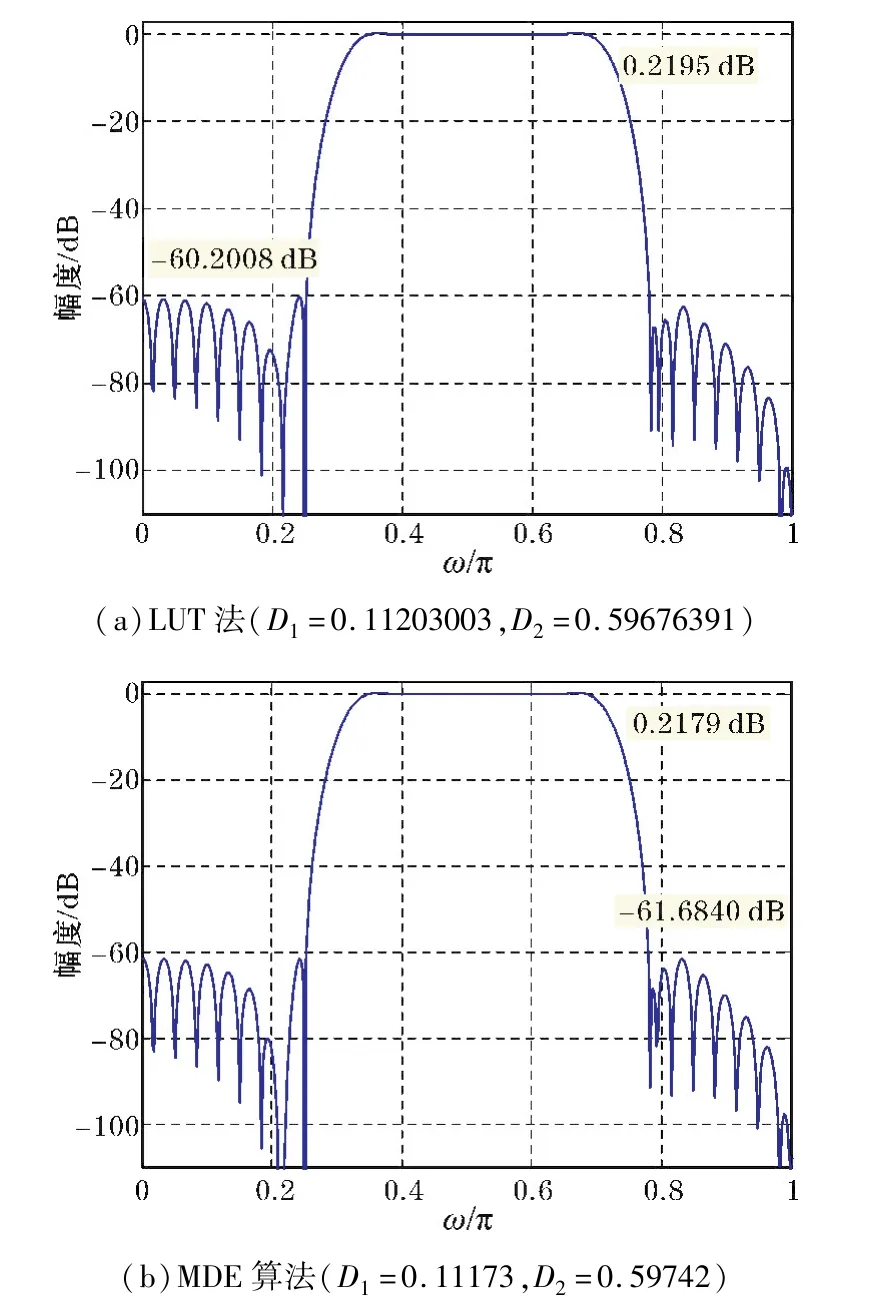
图7 Ⅱ型频率抽样法设计的FIR带通数字滤波器幅频响应曲线(N=60、ωs1=0.25π、ωp1=0.35π、ωp2=0.7π、ωs2=0.8π、D=2)

图8 设计FIR带通数字滤波器时MDE算法适应度进化曲线

4.4 实验结果数据对比分析

表1为实验结果数据对比,其中GA法数据为根据3个不同实验的适应度函数调用MATLAB7.0优化工具箱内置函数[x,fval]=ga(fitnessfun,nvars,options)[22]求得最优解的结果。可以清楚地看出,本文提出的MDE算法设计出的FIR高通、低通、带通数字滤波器各项指标均达到设计要求,具有比传统LUT法和GA法更为优越的性能(通带最大波动Rp更小、阻带最小衰减As更大)。由于MDE算法保留最好的个体到下一代中,所以在进化的过程中,适应度值是一随进化代数增加而单调上升的过程,算法逐渐收敛且收敛精度高。多次运算结果表明:MDE算法能以最短的时间、最为精确地搜索到全局最优解,且算法的健壮性更强。

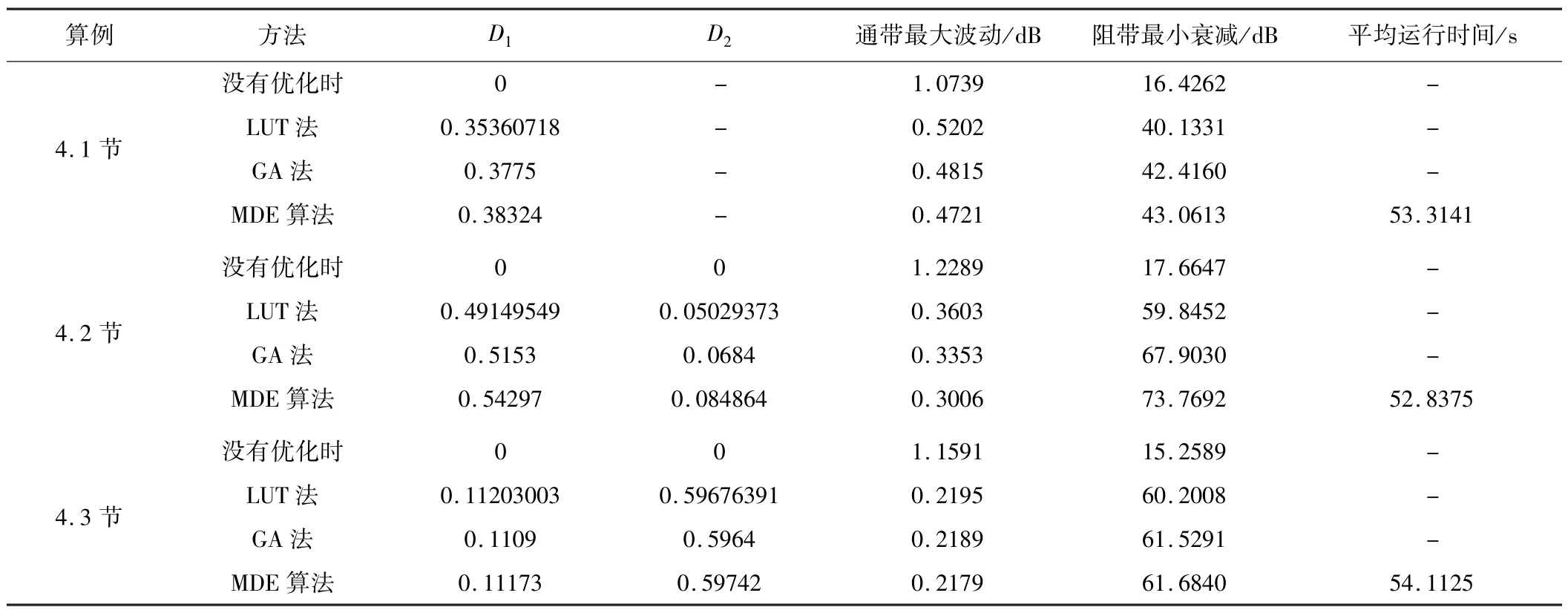
表1 MDE算法与LUT法、GA法的实验结果比较

5 结束语

本文采用Ⅱ型频率采样法设计FIR数字滤波器的基本原理,推导第一类线性相位FIR数字滤波器的Ⅱ型频率采样设计公式;针对传统差分进化算法的特点,提出一种改进的差分进化算法并设计相应的适应度函数,应用于采用Ⅱ型频率采样法设计FIR数字滤波器的过渡带样点值优化中。实验验证了改进差分进化算法控制参数少、结构简单、收敛速度更快、寻优精度更高、稳定性和鲁棒性更好,设计出的FIR数字滤波器性能显著优于传统查表法和遗传算法。若更改优化的目标函数,该改进差分进化算法也可以实现常规计算方法难以求解的高维、多目标、多模型、多峰值、非线性、非凸形等复杂环境中的函数优化问题和组合优化问题等。

致谢:感谢2022年成都信息工程大学大学生创新创业训练计划项目(202210621118);2021年成都信息工程大学电子工程学院教学改革项目对本文的资助