基于改进启发式优化算法的无线网络资源分配

张玉琴，梁 莉，张小洪，张建亮，冯向东

（1.成都理工大学工程技术学院，乐山 614000；2.成都理工大学数理学院，成都 610059；3.西南石油大学计算机科学学院，成都 610500）

引 言

无线网络中的资源优化［1］一直是热门研究课题，例如通过功率分配提升频谱和能量效率，正交频分多址（Orthogonal frequency division multiple access，OFDMA）和多载波非正交多址接入（Multicarrier non⁃orthogonal multiple access，NOMA）中的子载波分配［2］，时分多址（Time division multiple access，TDMA）中的时间分配，多址边缘计算（Multiaccess edge computing，MEC）中的计算迁移［3］，云无线接入网（Cloud⁃radio access network，C⁃RAN）中的远程无线电头选择［4］，以及无线传感器网络中的簇头选择等，通常描述为混合整数非线性规划（Mixed integer non⁃linear programming，MINLP）问题［5］，此类问题（NP难问题）求解难度较大。按照已有研究成果划分，此类问题一般有3类解决方案：博弈论方法、机器学习方法和元启发式算法。

博弈论提供了对独立理性参与者之间交互进行分析的数学工具。博弈论也被用于求解无线通信网络问题。如文献［6］使用联合匹配论和合作博弈来求解包含设备到设备（Device to device，D2D）通信的异构C⁃RAN中的资源分配问题，文献［7］通过对不可转移收益合作博弈的无线信道分配算法进行分析，约束平衡路由协议，且采用极小极大合作纳什均衡信道分配方案，得到了基于不可转移收益合作博弈的簇间公平路由和信道分配模型。但博弈论以理性响应为基础，依赖于可能会影响到参与者的策略和结果的数学模型，因此适用的场景非常有限。

机器学习方法也逐渐被用于在无线通信网络中实现性能和计算复杂度之间的平衡［8⁃9］。但机器学习并不适用于无线网络中的一些任务。例如，针对某个问题生成标准训练数据集并非简单任务，且在有些情况下无法实现。此外，利用非常大的数据集和大量参数对神经网络进行训练极为耗时。

为解决无线通信中复杂的资源分配问题，本文利用元启发式算法，因为任何元启发式算法中均会考虑到探索和开发之间的权衡。常见的元启发式算法有：粒子群优化［10］（Particle swarm optimization，PSO）、遗传算法［11］（Genetic algorithm，GA）、蚁群优化［11］（Ant colony optimization，ACO）算法、狼群优化［12］（Grey wolves optimization，GWO）算法和鲸鱼优化算法［13］（Whale optimization algorithm，WOA）。在这些优化算法中，WOA算法是高效的优化技术，具有较多优点。首先，WOA不需要计算梯度，基于梯度的算法在优化过程的每次迭代中需要计算并更新梯度和步长［13］，计算能力和存储要求极高。WOA能够放宽此类计算。其次，WOA对初始可行解不敏感。且WOA算法结合自适应机制，能够较好地平衡算法的探索和开发行为，由此更好地避免陷入局部最优解。最后，WOA易于实施且较为灵活，其适用于各种情况下的优化问题。

因此，本文利用WOA，通过模仿座头鲸的捕食行为求解无线网络中的各种优化问题。主要工作总结如下：（1）由于原WOA仅适用于连续且无约束的优化问题，提出了WOA的二进制版本（Binary whale optimization algorithm，BWOA），引入惩罚方法以处理优化约束。由此，可以求解各种优化问题，得到高质量解。（2）为分析WOA的适用性，本文分析并求解了无线网络中的资源分配问题，仿真结果表明，WOA算法能够以非常快的速度收敛，并取得与当前先进算法大致相当的性能。

1 基本理念和二进制版本

1.1 鲸鱼优化算法

WOA算法中，假定当前最优搜索代理为目标猎物，座头鲸则在迭代过程中向着最优搜索代理的方向更新位置。该行为可表示为

式中：A和C为系数向量；t为当前迭代；X*(t)为最优搜索代理的位置；|·|为绝对值，“·”表示逐元素相乘。系数向量A和C可计算为［13］

式中：a随迭代过程均从2～0线性递减，r为［0，1］中的随机向量。

式（3，4）旨在平衡探索和开发。式（3，4）中r均为随机数，为种群的位置更新提供随机性。式（3）中，随机数的范围为2～0。当系数向量A的元素值≥1时，探索完成；当系数向量A的元素值<1时，WOA则执行开发。为降低陷入局部解的概率，当WOA在进行开发时，参数C的元素值可以是［0，2］中的一个随机数。由此在优化的任何阶段促进开发探索。

在WOA算法中，气泡网攻击法和猎物搜索分别代表开发和探索这两个阶段。气泡网攻击法通过开发当前最优解来搜索局部区域，通过猎物搜索提升解的多样性以得到全局解。随着迭代次数增加，开发的重要性越来越高；而初始迭代时探索则更重要。研究人员对WOA的改进主要着眼于提高开发能力和探索能力，以及两者的平衡。例如文献［14］则使用莱维飞行轨迹以提升WOA的探索能力。

1.2 二进制鲸鱼优化算法

原始WOA算法针对连续优化问题，然而，很多问题被表述为混合整数规划（Mixed integer pro⁃gramming，MIP）问题，其中每个变量值可能是离散或二进制的。为处理组合优化，本文提出了WOA算法的二进制版本。BWOA算法的伪代码如算法1所示。除了位置向量更新外，BWOA采用了与WOA相同的步骤，BWOA的计算复杂度也是O（NDT）。其中N为鲸鱼种群，D为搜索代理的维度，T为最大迭代次数/代数。

算法1 二进制WOA算法的伪代码

（1）初始化鲸鱼种群Xi，i=｛1，2，…，N｝，迭代t=1，最大迭代次数Imax，并设定终止标准ϵ。

（2）计算搜索代理的适应度，并识别最优搜索代理X*(t)。

（3）repeat

（4）fork←1 toM（鲸鱼数量）do

（5）更新a，A，C，并生成pBWOA。

（6）ifpBWOA<0.5 then

（7）if|A|<1 then

（8）通过式（1）更新D，通过式（5）更新σsem。

（9）基于式（6）更新位置X(t)。

（10）else

（11）选择一个随机的Xrand，并更新D。

（12）通过式（8）更新σsp，通过式（9）更新X(t)。

（13）end if

（14）else

（15）通过式（1）更新D。

（16）通过式（7）更新位置X(t)。

（17）end if

（18）end for

（19）计算每个搜索代理的适应度。

（20）更新最优搜索代理的X*(t)。

（21）增加迭代索引t=t+1。

（22）untilt>Imax或

（23）Output：最优适应度数值和最优鲸鱼位置。

在WOA中，基于最优搜索代理的位置（可以使可行集合内任何连续数值）进行位置更新，BWOA则基于数值1和0之间的切换进行位置更新。根据座头鲸螺旋移动计算出的概率，来决定当前位的变化。此外，传递函数中考虑了一些概念：（1）数值应在［0，1］内，因为传递函数表示了将位置从0变为1的概率，反之亦然；（2）传递函数应该与座头鲸位置和猎物之间的距离成正比，即远离最优搜索代理的搜索代理应该具有较高概率。具体改动解释如下。

缩圈机制：根据以下传递函数计算出步长为

式中D和A分别通过式（1，3）计算得出。可将σsem用于决定是否对位值进行切换的概率。搜索代理的位置被修改为

式中：pBWOA为［0，1］中的一个均匀随机数，C（·）表示补充补运算。为了得到二进制数的补码，可简单地对二进制数中所有位进行取反，即将0换为1，反之亦然。

螺旋更新位置：螺旋更新位置机制中的位置可计算为

式中σsup为步长。

搜索猎物：步长计算为

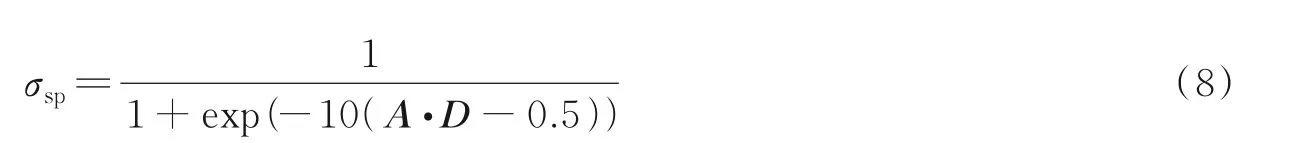
式中A和D分别通过式（3，1）计算得出。由此，搜索代理的位置可更新为

一般可使用不同的传递函数，将连续搜索空间映射到离散动作。本文将具有不同斜率的Sigmoid函数创建为S形传递函数，可表示为Tα（·），其中，α为S形传递函数的斜率。举例来说，T（2）（x）=1/（1+exp（−2x）），T（1）（x）=1/（1+exp（−x）），T（1/2）（x）=1/（1+exp（−x/2））。将座头鲸位置和猎物之间的距离表示为x。对于给定的距离x，随着斜率α的增加，改变位值的概率也会变大。因此，对于相同数值的距离x，T（2）返回的概率高于T（1），T（1/2）则返回最低的概率。从图1中可观察到这一点。高效地利用这些传递函数，能够进一步提升BWOA算法的性能。

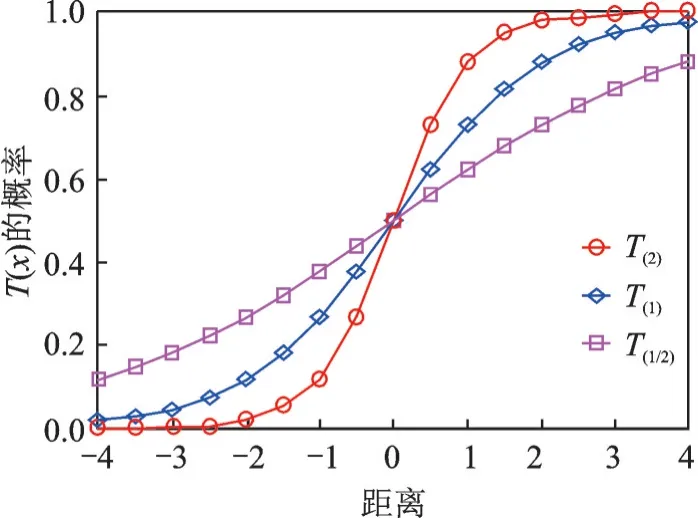
图1 S形转移函数的样例Fig.1 Example of S-shaped transfer function

1.3 算法的约束

由于原始WOA算法针对无约束优化问题，在求解约束问题时，需要采用高效的约束处理技术。一些较好的约束处理方法包括惩罚方法、带容差的等式、可行性规则、目标和约束相分离、随机排序、ϵ约束方法以及多目标方法等。惩罚方法是广为使用的简单方法，其尝试通过合并目标和约束，将约束问题转换为无约束问题［15］。下文将介绍惩罚方法的基本理念。元启发式优化中的其他约束处理技术可参阅文献［16］。

考虑一个使所有可行x中的f0（x）最小化，并满足m个不等式和p个等式约束的问题

惩罚函数可定义为

式中P（x）为惩罚项，其可定义为

式 中：µi≥0，νj≫1为 惩 罚 因 子，为 便 于 实 施，令µi=µ，∀i，νj=ν，∀j。若fi（x）≤0，索 引 函 数Fi（fi（x））=0；若fi（x）>0，F i（fi（x））=1。同 理，若hj（x）≠0，索 引 函 数H j（hj（x））=1；若hj（x）=0，H j（hj（x））=0。扩展目标函数ϕ（x）旨在降低不可行解的适应度，并增加可行解的适应度。如式（11）所示，添加到解的适应度的惩罚值主要由惩罚因子所控制。若惩罚因子过小，可能无法对不可行解作出足够惩罚，由此在优化过程受到影响。若使用过大的惩罚因子，会造成可行解的质量较低。此外，WOA算法鼓励对不可行解的开发，特别对不相连的可行区域更是如此。一般来说，惩罚因子µ和ν为1013～1015。

1.4 复杂度分析

对于有约束问题，WOA的计算复杂很大程度上取决于等式和不等式约束的数量。与p个等式约束和m个不等式约束相对应的索引函数计算复杂度分别为O（Np）和O（Nm）。如表1所示，将这些复杂度与原始WOA复杂度相加，则WOA求解约束优化问题时每次迭代的计算复杂度为O（N（m+p+D）），其中，D为搜索代理的维度。由于WOA最多迭代T次，则WOA求解约束优化问题的复杂度为O（TN（m+p+D））。而所提BWOA则无需处理索引函数的复杂度，复杂度更低，其复杂度为O（NDT）

表1 复杂度比较Table 1 Comparison of complexity

对于无约束问题，WOA与提出的BWOA的复杂度一样。近似凸问题会产生M个优化变量，迭代次数为T次，搜索代理数量为N，因此，其复杂度为O（NMT）。

2 实验案例

本章将分析BWOA在求解无线网络中2个基本优化问题的应用：保密率最大化的功率分配问题；移动边缘计算迁移。第1个案例是无约束连续优化问题中的应用，第2个案例针对MINLP问题。

2.1 保密率最大化的功率分配

2.1.1 系统模型和问题定义

考虑包含M个用户的干扰受限无线网络，每个用户可视为一条通信链路，包含一个单天线发射器和一个单天线接收器。pi表示用户i的发射功率，gij表示从用户j到用户i的信道增益。用户i的数据速率为

在单天线窃听器处用户i的窃听率为

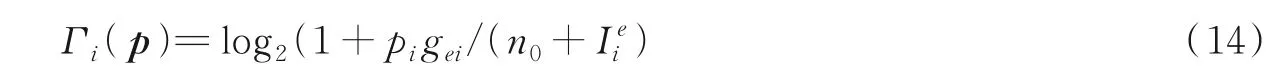
式中pmaxi为用户i的峰值发射功率。

2.1.2 仿真结果分析

本文采用与文献［17］的仿真相同的参数。对路径跟随程序的初始可行点p（0）进行初始化，即

图2给出了随迭代进行，文献［17］的路径跟随方法和本文BWOA算法的收敛演变。如图2所示，两个算法均可快速收敛，路径跟随方法需要12次迭代（如图2，收敛处的迭代次数X为12，频谱效率Y为1.348 b/（s⋅Hz），基于BWOA的算法则需要26次迭代（如图2，收敛处的迭代次数X为26，频谱效率Y为1.347 b/（s⋅Hz）。但路径跟随方法中，每次迭代均会涉及一个凸问题的求解。由于近似凸问题会产生M个优化变量（即pi，i∈｛1，2，…，M｝）和M个线性约束（即0≤pi≤pmax，i∈｛1，2，…，M｝），路径跟随方法的计算复杂度为O（T（M2M2.5+M3.5）），T=12。与文献［17］不同，BWOA算法的每次迭代中，用户在更新其发射功率时会遵循最优搜索代理。对于无约束问题的计算复杂度为O（NMT），T=26，N=30（搜索代理数量）。因此，基于BWOA算法的计算复杂度较小，这对于包含大量连接的实际应用来说非常重要。此外，两种算法几乎得到相同结果，但与文献［17］的算法相比，基于BWOA的算法的计算复杂度较低，并实现了较高性能。

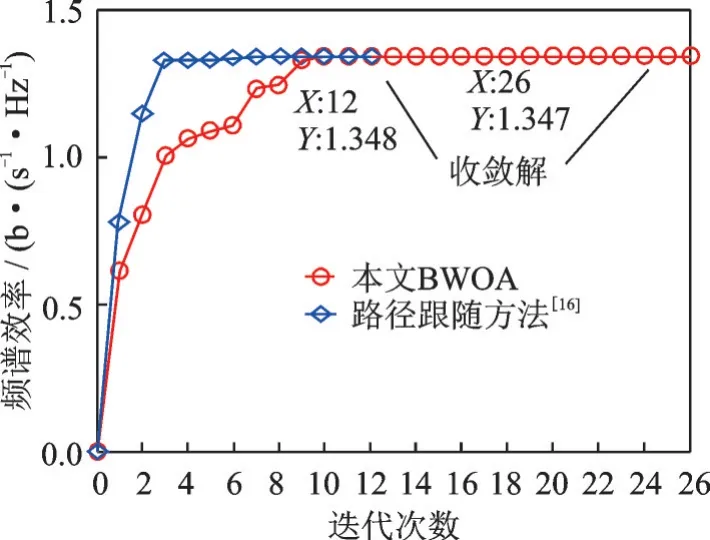
图2 算法的收敛演变Fig.2 Convergence evolution of algorithms

2.2 移动边缘计算迁移

本小节通过实验，比较本文BWOA算法与文献［18］的启发式⁃迁移决策算法（Heuristic offloading decision algorithm，HODA）在系统总计算开销和迁移百分比方面的性能差异。

2.2.1 系统模型和问题定义

考虑一个与eNB位于同处的MEC服务器和M个用户的MEC场景。每个用户的计算任务为Ii=｛Di，Ci｝，其中Di为输入大小，Ci为完成任务所需的CPU周期数。ai为用户i的迁移决策。若任务Ii被迁移，则ai=1；否则，ai=0。用户i的完成时间和能耗分别表示为和其中和分别为本地/远程执行任务Ii式用户i的任务完成时间和功耗。根据文献［18］其中，为用户i的本地计算能力，α=10－11，γ=2，fi为MEC服务器分配至用户i的计算资源，ς为功率放大器效率，Ri为用户i的数据速率。假定子载波分配是正交且预定义的，则数据速率Ri可表示为

式中hi为从用户i到eNB的信道增益。为了通过计算迁移，最大程度改善完成时间和能耗，可将整体效用定义为

式中和分别为完成时间和能耗方面的用户偏好。通过优化计算迁移决策和资源分配，以最大化整体效用的问题可表示为

2.2.2 仿真结果分析

实验使用与HODA相同的仿真参数集。文献［18］将原始问题分解为两个子问题：（1）针对给定的迁移决策，优化计算和通信资源；（2）优化迁移决策。此外，取200次实现的结果的均值绘制图表，且每次实现中随机分配用户位置。

不同用户数量时的系统性能比较如图3所示，由图3可知，随着用户数量增加，用户范围更加广泛，有着各种不同的信道条件、本地计算能力和计算任务，因此两种算法均能够持续改善系统效用。每个用户在计算迁移中需要与更多用户竞争，且子载波数量是有限的，因此一些用户不被允许迁移，虽然事实上这些用户依然可以从远程执行中受益。本文算法的计算复杂度为O（N（1+M）），而HODA和最优解的计算复杂度分别为O（M3）和O（2M）。当用户数量在2～10间变化时的性能比较如图3所示，可以看出，本文算法与HODA的求解性能大致相当。用户数量M=8时，本文算法的系统效用为1.730，HODA的系统效用则为1.731 1。此外，HODA能够通过穷举搜索将其性能保持在最优解的5%范围内。由此，本文算法能够以较低计算复杂度实现良好性能。BWOA在优化过程中涉及探索和开发，因此可将其视为全局优化器。因此，本文BWOA在移动边缘计算迁移中性能更优。

图3 不同用户数量时的系统性能比较Fig.3 Comparison of system performance with different number of users

3 结束语

本文介绍了WOA及其在无线通信网络的资源分配中的应用。为了证明所提WOA适用于无线通信网络，本文分析了两个无线网络资源分配问题：保密率最大化的功率分配问题和移动边缘计算迁移。第1个案例是无约束连续优化问题中的应用，第2个案例是针对MINLP的问题。实验结果表明本文方法具有优秀的计算性能，收敛速度快，能较快达到全局优化。本文针对原始WOA算法难以解决非连续优化问题的缺陷进行改进，但其他更多的离散问题的优化依然有待研究。另外，将所提算法应用到移动边缘计算也是未来研究方向之一。