基于NSGA-II算法的寒区河道清淤工程工期成本优化
2022-12-13丰小华FENGXiaohua
丰小华 FENG Xiao-hua
(中铁十七局集团第三工程有限公司,石家庄 050000)
0 引言
近年来,随着国家对环境治理的重视,河道综合治理工程项目逐渐增多。河道综合治理工程项目涉及水利、水运、环境、生态和城市景观等多个领域,具有规模大、投资多、涉及面广、工序多、周期长、技术复杂等特点,且受到当地气候、施工环境和社会等非技术因素的影响,如何在诸多因素的影响下,组织安排好施工进度计划与资金、机械及人员之间的投入是实现工程建设项目效益的关键。
施工工期和成本的优化主要是通过建立优化数学模型,求得在限定约束条件下的最优解。河道综合整治工程施工的工期-成本优化属于多目标组合优化问题,在保证工程可持续运行,各工序安全有序施工的同时,实现工期最短和成本最优,达到提高施工企业经济效益的目的。
随着优化算法和计算机技术的发展,基于数学模型的多目标优化控制理论,特别是遗传算法以计算速度快、容易求得最优解而在大型工程建设项目中得到广泛应用。胡良明等[1]基于遗传算法对农村供水管网进行了优化设计。游健[2]针对传统大坝安全综合评价指标算法的局限性,提出基于改进的遗传算法建立大坝安全评价模型。李斌[3]以某实际水利工程为研究对象,基于多目标优化遗传算法对工程工期,成本与质量优化的方法,验证了该算法工程实际施工进度计划优化中应用的可行性;李竞克等[4]从投资最少,工期最短和最佳质量三个方面建立多目标工程施工进度目标函数,对某实际工程仿真,进一步验证了多目标遗传算法能较好地求解施工进度目标函数最优解,且能够提供多种优化方案。刘东海等[5]以某高心墙堆石坝为例,运用遗传和声算法对其施工进度进行综合优化,从而实现了工程质量,安全与施工进度的均衡安排。
基于以上分析,本文将改进的GA算法运用到河道清淤工程实例中,通过引入带精英策略的非支配排序遗传算法NSGA-II进行工期-成本的多目标优化和方案优选,实例应用表明本文方法的有效性与合理性,可为实际工程施工进度优化控制提供一定指导和借鉴。
1 工程概况
伊通河北北段南起四化闸,北至万宝拦河闸,河道长度约13公里。通过现场调查研究,发现河道上游及支流来水水质较差为劣五类水质,周围还存在多处点源污染、面源污染、内源污染汇入量大,同时全河段还存在不同程度的淤积情况,造成河道内大量底泥淤积的堆积,污染状况的恶化,严重影响了周边环境,给社会经济、环境的可持续发展带来严峻挑战。
2 工期-成本数学优化模型的建立
2.1 优化原理概述
本文确定以河道清淤施工进度最快,施工成本最低为目标,以每个工序的工作持续时间和消耗的成本上下限为约束条件,建立一种基于多目标优化的数学模型,并采用多目标遗传算法NSGA-II进行求解,实现河道清淤工程工期-成本的优化,从而尽可能的提高施工质量,加快施工进度,降低施工成本。
2.2 目标函数
以清淤施工工期最短,成本最低为优化目标,构造如下目标函数:
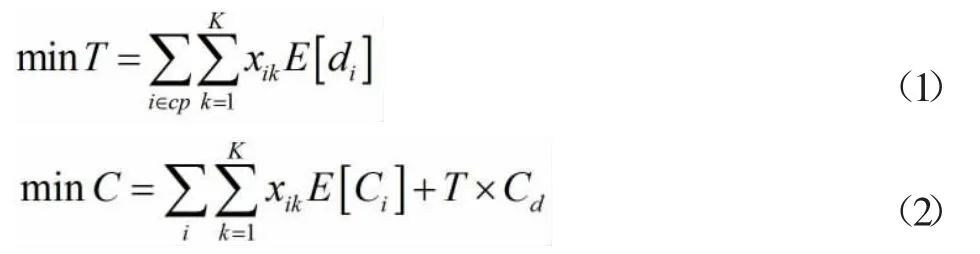
式中,T为优化工期;C为优化成本;i为工序;k为每个工序的选择方案;xik为0-1二元决策变量;di为作业i的工作时间;Cd为间接成本。
2.3 约束条件
以各工序的持续时间和消耗的费用上下限为约束条件,建立如下约束方程:

式中,i为工序;k为每个工序的选择方案;K为总方案的数量;xik为0-1二元决策变量;j为作业i的紧后作业;ti为作业i的工作开始时间;tj为作业的开始时间;IC为间接成本;di为i作业的工作时间;B为成本预算。
3 带精英策略的非支配排序遗传算法
3.1 算法原理
NSGA-II算法自2000年被Deb K等[6]提出以来,广泛应用到工程的各个领域解决多目标优化问题,它是在遗传算法实现选择交叉变异的基础上加入非支配排序,降低了计算非支配序的复杂度,扩大了采样空间,以此保留种群中好的个体,利用适应度函数保持群体父代的多样性,尽量缩短目标函数的个数。该算法的核心就是协调各个目标函数之间的关系,找到使得各个目标函数都尽可能达到期望值的最优解集。
3.2 算法设计
根据上节所描述的目标函数和约束条件,对于工期-成本多目标优化问题,一般情况下需要对算子进行设计。因组合方案多为非支配解,如果利用非支配排序的方法进行计算,计算效率极低还不利于算法收敛。本文在此以传统遗传算法为基础,引入精英策略算子,扩大采样空间,同时进行拥挤度和拥挤度比较算子计算,提高计算效率,加快算法收敛速度,提高算法的鲁棒性,保证了计算结果的稳定性。NSGA-II算法的流程图如图1所示。其中gen为进化代数,N为种群数量。
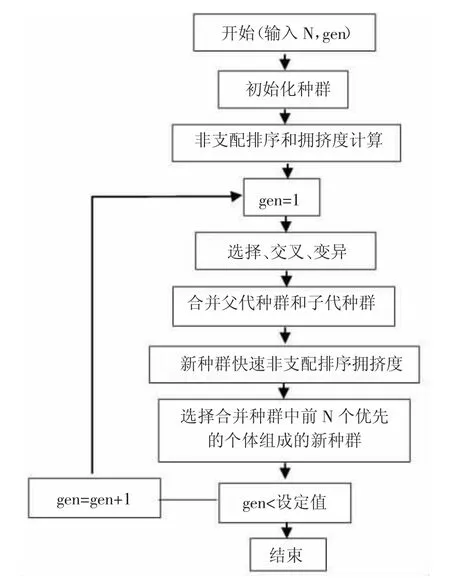
图1 NSGA-II算法的流程图
4 工程实例
根据方格网布置勘探点,经计算,四化闸至万宝闸段水利高程以上淤泥量约240万m3,采用干式清淤+半干式清淤结合的方式,总体施工工序分为施工准备、施工围堰、排水导流、淤泥开挖、淤泥倒运、外运处置、工程验收等,计划投资7600万,工期365天。结合施工组织安排以及业主对现场的一些相关节点要求,同时综合考虑进度、成本、工期要求,进行不同条件下的人员、设备、材料、机械的投入的推演,得到不同工期下的成本,形成表1所列的相关施工参数。
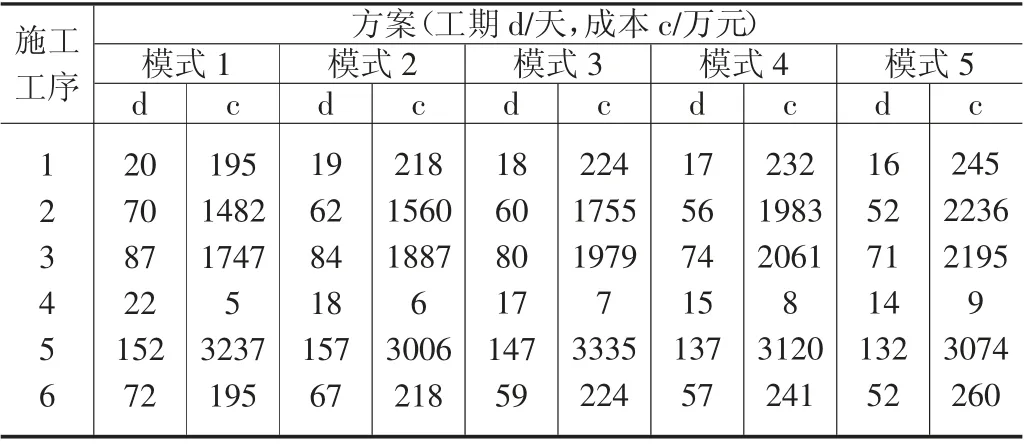
表1 伊通河北北段清淤施工相关参数
4.1 优化目标
优化问题三要素是决策变量、目标函数、约束,单目标和多目标和优化问题的不同之处是单目标的解是单一的是可明确的,得到的最终解能够达到最值,而对于多目标优化,目标函数和约束条件可能存在多个共存,且相互之间会存在冲突,它的解并非唯一,无法直接比较优劣性,最优解是一组由众多Pareto最优解组成的最优解集合,工期和成本在一定意义上就是相互矛盾的,要使两者同时达到最优几乎不存在,很难找到一个最理想的解。在面对实际的工程情况下,我们的决策方案要结合实际,不能脱离现实环境,因此最终求解的工期和成本不一定是最优,还要面临很多实际存在一些问题,所以我们要合理的决策工期和成本之间的关系。针对伊通河北北段清淤施工问题,更是会受到诸多因素的影响,因此我们采用多目标优化数学函数,将工期最短,成本最低设定为优化的目标。
4.2 优化原理
对于本清淤工程项目的工期是各个施工工序所持续时间之和。在整个河道生态治理工程中,清淤工程是首当其冲的一个施工任务,是后续各项工程展开施工的基础,其进展快慢将直接影响项目总工期。清淤工程的施工能直接解决淤泥引起的一系列环境问题,对于生态环境的治理能达到立竿见影的效果。我们希望用最短的工期完成清淤工程的施工,从而降低各种施工成本,创造更大的综合经济效益。
按照工程成本构成划分,将河道清淤工程成本分解为直接成本和间接成本,直接成本包括人工费、材料费、施工机械使用费和其它费用等,间接成本包括施工管理成本和其它成本。
构成施工成本的各项工作内容,完成任务的工期越短,直接成本与之对应增加;间接成本则随着工期的延长相应增加。工期和成本之间相互影响,互相制约,存在一定的联系,直接费和工期呈现反比例关系,间接费和工期呈现正比例关系,因此两者之间必存在一个点使得直接费和间接费之和达到最低谷,这就是我们要研究的工期和成本的优化,在实际施工中,如何通过合理的施工组织安排,配置资源,确定各工序的施工时间,从而找出工期和成本的均衡点。在构建的工期成本模型中,利用遗传算法,进行非支配排序,对伊通河清淤施工的工序各个模式进行了筛选,在巨大的搜索空间内寻找这个最佳点,图2中所示的A点即为要优化求解的点。
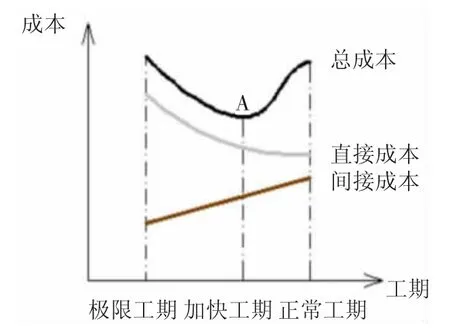
图2 工程项目施工成本的构成
4.3 优化结果
以表1中所列数据为基础,应用MATLAB软件编制NSGA-II相关算法程序,最终所得优化结果如图3~图5所示,工期成本综合优化的满意解部分的结果见表2。
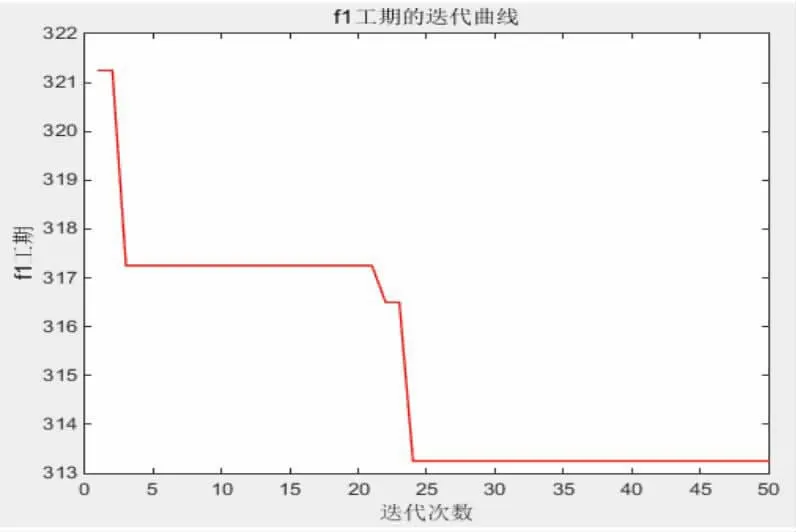
图3 工期-迭代曲线

图5 多目标算法优化得到的作业甘特图

表2 工期-成本优化计算结果(部分)
从NSGA-II算法优化计算所得的工期-迭代曲线结果可知,在资源配置均衡条件下,工期随着迭代次数的增加最终趋于稳定,说明该算法能搜索到工期的最小值。
图4和图5分别为工程-成本权衡图和多目标算法优化得到的作业甘特图。从工期成本的权衡图可看出工期与成本二者之间呈反比,缩短工期则会引起费用增加,这个结论是符合工程实际情况的。从解得搜索效率可知,搜索空间中有56个可行解,NSGA-II算法能够得到一系列分布均匀、多样性较好的最优解集,最优解为工期315天,相比较计划工期节省56天,优化后的成本为6801万元,相比较计划投资节约了11%费用。由此可见,运用NSGA-II算法进行河道清淤工程工期-成本的多目标优化求解,具有可观的经济效益和实用性。
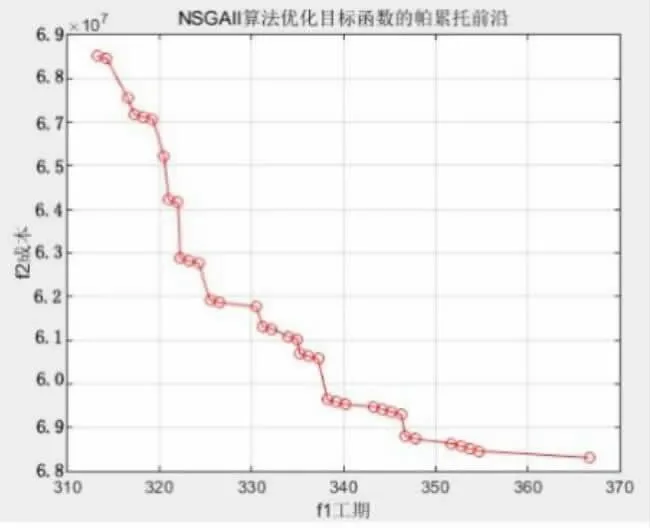
图4 工期-成本权衡图
5 结论
本文将NSGA-II算法应用到河道清淤施工工期和成本优化中,优化结果符合工程实际,解决了工程的工期和成本的优化问题,NSGA-II算法的应用提高效率,同时也验证了工期-成本均衡优化模型的合理性和可操作性,可为实际工程提供理论的依据和较好的指导作用。
