高中学生计算思维水平现状调查与分析*
2022-12-13孙爽魏文清赵瑞陈莹
孙爽 魏文清 赵瑞 陈莹
(1.吉林师范大学 计算机学院,吉林 四平 136000;2.四平市第一高级中学,吉林 四平 136000)
一、引言
计算思维最早由麻省理工学院的西蒙·派珀特(Seymour Papert)教授于1996 年首次提出[1]。2006 年,周以真教授发表了题为《Computational Thinking》的文章,并对计算思维进行了系统的论述[2]。自计算思维概念提出以来,就受到各国的广泛关注和高度重视。我国《普通高中信息技术课程标准(2017 年版)》也将计算思维列为信息技术学科核心素养之一,并且是该学科核心素养培养的核心议题[3]。
计算思维的评价是培养学生计算思维能力水平至关重要的一环,它不仅是开展教学活动的依据,还是检验计算思维培养成果的重要手段[4]。国际上有关计算思维评价工具的类型有多种,基于量表的评价,如Korkmaz 等学者设计开发的计算思维量表(Computational Thinking Scale,简称CTS[5]);基于试题的评价,如Bebras Tasks;基于系统环境的评价,如Dr.Scratch 编程软件[6][7]。CTS 与其他类型工具相比更关注对学生计算思维观念方面的评价,并且在学界获得了较高的认可。因此,本文采用Korkmaz 等学者根据国际教育技术协会(ISTE)定义的计算思维理论框架设计开发的,包含创造力、算法思维、批判性思维、协作学习、问题解决五个维度的计算思维量表。并通过相关性分析和探索性因素分析来检验量表的合理性,利用单因素ANOVA检验探究计算思维能力在性别、年级、生活环境等方面的差异。根据分析得到的结果提出相应建议,为一线教师在信息技术课程教学中培养学生的计算思维提供参考。
二、调查问卷的设计
(一)问卷各部分说明
问卷第一部分为学生基本信息,共3 道题,了解学生的性别、年级、生活环境等方面情况。第二部分为计算思维量表,包含创造力、算法思维、协作能力、批判性思维和问题解决五个维度,共29 道题。量表采用Likert 五点计分法,每题五个选项,包括非常符合、基本符合、有点符合、基本不符、非常不符,分别赋分5 分、4 分、3 分、2 分、1分。计算思维量表各维度题目与描述如表1 所示。

表1 计算思维量表各维度与描述
(二)问卷的预测与调整
本次预测共回收有效问卷314 份,利用SPSS21.0 软件对回收的有效问卷数据进行统计,并对量表进行相关性分析,以相关性分析为基础对量表的信度、效度进行验证,进而检验量表中的各个题项是否符合要求,将不符合要求的题删除,最后形成一份科学严谨的问卷。
1.相关性分析
笔者对量表进行项目分析,首先求出该量表中各题项的决断值(CR 值),再考察各题项与量表总分的相关性是否显著,将未达到显著水平的题项给予删除。具体操作是:将314 名学生所得的总分计算出来,由高到低进行排序,把成绩中的前27%作为高分组,组别为1,后27%作为低分组,组别为2,再求出高、低两组学生在各题项得分的平均值的差异显著性,利用独立样本T 检验的方法进行检验。若有题项未达到显著水平,应将其删除。本调查问卷第二部分各个题项得分与量表总分的相关性如表2 所示。

表2 各题项得分与量表总分的相关性
从表2 可以发现,问题解决维度中的PS1 题和PS2 题不能反映出被测试学生的计算思维能力水平(P>0.05),这两道题均未达到显著性差异,因此应删除问题解决维度中的这两道题,删除后,笔者又对该量表进行重新编号。
2.量表效度检验
通过KMO 和Bartlett 的球形度检验来判断量表的有效性。检验得到KMO=0.923,x2=6861.277,p<0.001,说明本量表数据适合进行探索性因子分析。
借鉴阿科约尔探索性序贯设计研究思路[8],对样本数据进行探索性因子分析。采用主成分分析法提取因子,选取最大方差法进行旋转,以特征值大于1 作为提取因子的标准,对低载荷值(小于0.40)进行忽略。经检验,共提取5 个主成分因子,累积解释方差为73.013%,各题项的因子载荷系数均大于0.4,但CA8 和AT1 题项均出现了交叉载荷现象。经讨论分析后,决定删除这两个题项,最终形成共有25 个题目的计算思维能力调查量表。
3.量表信度检验
在进行效度分析后,为进一步验证量表的可靠性,通常采用克隆巴赫α系数(Cronbach’s α)对量表进行信度检验。结果显示:总调查量表Cronbach’s α 系数为0.917,各维度系数依次为αCA=0.901、αAT=0.933、αCL=0.936、αCT=0.875、αPS=0.909,量表不管是总信度系数还是各维度信度系数的结果均在0.8 以上,这说明该调查量表的可靠性很好。
“互联网+”亲职教育这一新兴领域,是时代变革的产物,是对传统教育的颠覆,深刻影响了教育的各要素,倒逼教育改革。这一艰巨的任务,呼唤强有力的主导者来组建活力、规范、系统的发展格局,而政府具有义不容辞的责任。
(三)问卷的正式发放与回收
根据前面预测问卷结果的分析,将原始问卷中不合理的题项删除,形成本研究的正式调查问卷,包括学生的基本信息和计算思维能力两部分,共28 道题。本研究的被试对象为某省普通高中一、二年级的学生,调查对象共有310 人,回收有效问卷290 份,其中男生110 名,女生180 名。高一年级学生152 人;高二年级学生138 人。城市学生177 人;农村学生113 人。
三、调查结果分析
(一)计算思维水平的总体现状
本研究通过描述性统计对学生计算思维及各维度能力情况进行了分析,其分析结果如表3 所示。
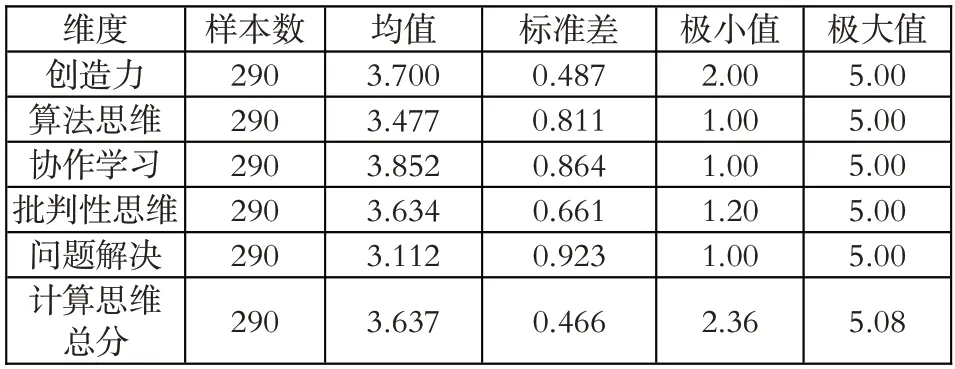
表3 计算思维能力描述性统计分析表
由表3 可知,计算思维能力的平均分为3.637,而量表中3=有点符合,这表明学生的计算思维处于中等水平。就计算思维的各维度而言,学生从高到低的得分依次为:协作学习、创造力、批判性思维、算法思维和问题解决维度。结果表明高中学生的协作学习能力较高,可以相互配合开展合作学习,这可能是由于近年来基础教育中各学科都强调应用小组合作探究的学习模式,学生在学习过程中已经养成了基本的沟通合作能力。但是学生的问题解决能力较低,这可能是因为2003 版课标下,教师在教学过程中虽然注重了三维教学目标的培养,常见以任务驱动法进行课堂教学,但是缺乏对教学内容的整体考虑,仍然是以课时为单位进行教学设计,学生基础知识比较牢固,但是缺乏应用情境下的自主计划、探究和实施过程,不能把所有学科知识灵活整合用以解决问题。这一点也反映了学生计算思维能力的不足,在今后的教学中需要培养学生界定问题、抽象问题、分析问题、建立结构模型、运用合理的算法解决问题的能力,实现计算思维培养的终极目标。
(二)计算思维水平与学生基本情况的差异性分析
1.计算思维水平与性别的差异性分析
本研究通过单因素ANOVA 检验,了解学生性别对计算思维及其各维度的影响,其分析结果如表4 显示。不难发现,男生的计算思维平均分为3.711,女生的计算思维平均分为3.591,即男生的整体计算思维水平高于女生。由P=0.034<0.05 可知,学生的计算思维水平与性别之间存在显著差异。在各维度方面,除协作学习能力之外,男生在其他维度上的得分均高于女生,尤其是问题解决能力更为显著,算法思维和批判性思维的差异性基本相当。由此可以看出,学生的计算思维在性别上确实存在较为明显的差异,这就需要教师在教学过程中对任务分配、内容安排进行有目的的规划和调整。
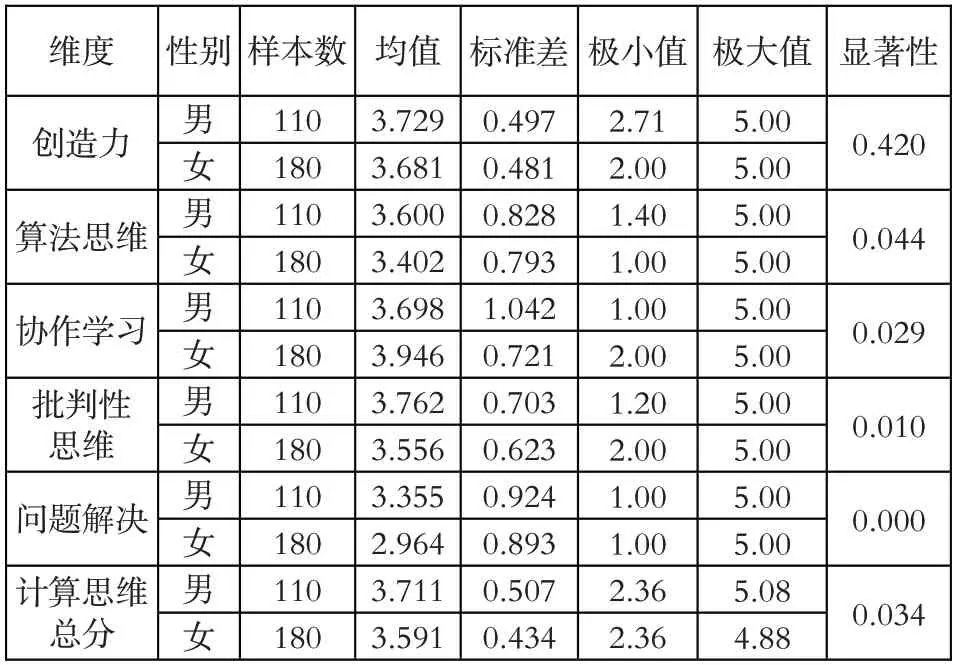
表4 计算思维水平与性别的差异性分析
2.计算思维水平与年级的差异性分析

表5 计算思维水平与年级的差异性分析

(续表)
由表5 可知,高一、高二年级学生的计算思维平均分分别为3.700 和3.567,即高一学生计算思维水平略高于高二学生。由P=0.015<0.05 可知,不同年级学生的计算思维水平存在显著差异。在各维度方面,除创造力之外,高一学生在其他维度上的得分均略高于高二学生,且在算法思维和问题解决能力上存在较明显差异。这可能是因为高中信息技术课程一般都在高一开设,在必修课结束后,高二一般就不再进行信息技术课程的学习,导致学生的整体水平稍有下滑。
3.计算思维水平与生活环境的差异性分析
本研究采用单因素ANOVA 检验的方法,探究生活环境对计算思维水平及其各维度的差异,其分析结果如表6 所示。
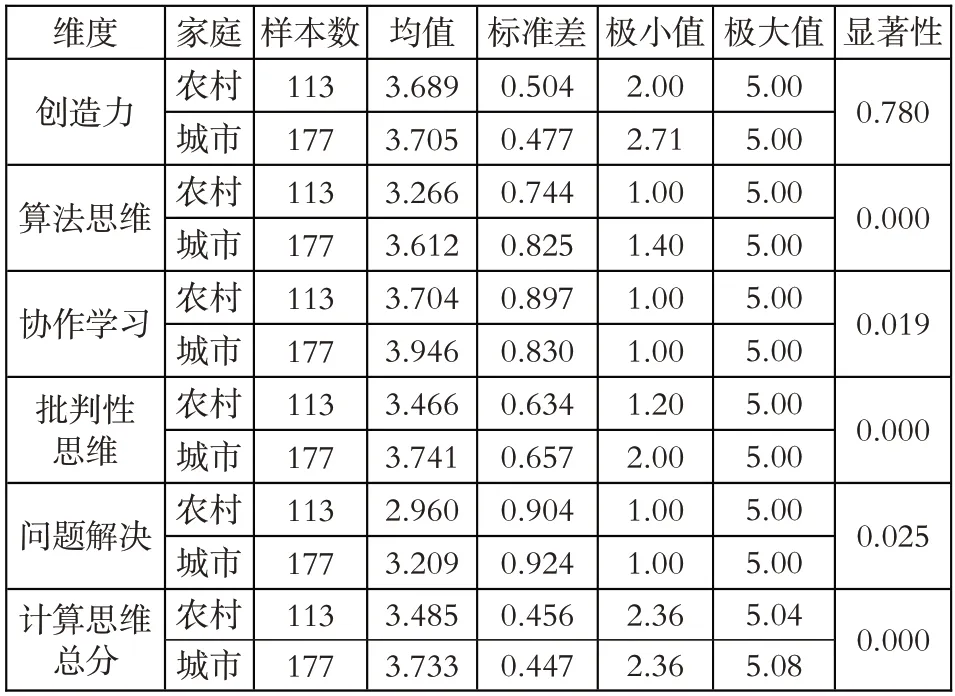
表6 计算思维水平与生活环境的差异性分析
由表6 可知,城市学生与农村学生的计算思维平均分分别为3.733 和3.485,即城市学生的计算思维水平明显高于农村学生。由P=0.000<0.05 可知,不同生活环境下学生的计算思维水平存在显著差异。在各维度方面,除创造力之外,城市学生在其他四个维度上的得分均明显高于农村学生,且存在显著性差异,尤其是算法思维的差异性最大。这也表明创造力是一种原动力,受学生的生活环境影响不大,但是其他方面的维度受学生的视野大小、教学环境、信息素养、培养模式等因素的影响较多。
四、研究结论与建议
(一)切实落地新课改,全面提升学生的计算思维水平
整体上,目前高中学生的计算思维水平处于中等程度,在各维度方面,学生的协作能力较高,创造力和批判性思维能力次之,而算法思维和问题解决能力较低。究其原因,笔者认为是近年来各学科都强调应用小组合作探究的学习模式,大大提高了学生的协作能力。目前,高中信息技术课程考核方式仍然以会考为主,过程性考核并没有真正落地。教师在教学中虽然注重了三维教学目标的培养,但缺乏对教学内容的整体考虑,仍然以课时为单位进行教学设计,学生缺乏应用情境下的自主计划、探究和实施过程,导致问题解决能力没有得到充分锻炼。这也充分说明新课程标准建议高中信息技术课堂采用基于项目的学习是切实有效的。教师在教学中通过创设真实的问题情境,调动学生学习的积极性,按照“学主教从、以学定教、先学后教”的专业路径,把项目整合于课堂教学中,引领学生解决生活中的实际问题。学会分析问题、批判问题、合理计划、主动探究,从而有效提高学生解决问题的能力。
(二)重视影响计算思维的差异性因素,提高学生在项目活动中的有效参与
学生的计算思维水平与性别、年级、生活环境等方面均存在显著差异。在性别方面,男生整体的计算思维水平略高于女生。就各维度而言,女生的协作能力明显高于男生,男生则在问题解决能力上显著高于女生。这可能是男生相较于女生更具有好奇心,愿意尝试新事物;更善于发散思维,寻求解决问题的不同方法。这也启示教师应重视对女生计算思维的培养,教学中可以根据学生的个性差异以及知识水平,将男女生混合分成若干小组,共同开展探究活动,充分发挥女生的协作能力,让学生通过合作发散思维,促进学生在学习上的互相帮助和共同提高。
在年级方面,高一学生的整体计算思维水平高于高二学生,尤其是算法思维和问题解决能力最为显著。这可能是因为高一学生经过一学年信息技术课程的学习,在算法思维、批判性思维、问题解决能力上有明显的提高。进入高二后学生各科学习任务不断加重,而且大多数学校不再开设信息技术课,这也导致高二学生的计算思维水平明显低于高一学生。因而,建议学校可以通过STEAM 课程或者其他校本课程的形式提高学生的信息技术学习机会和使用机会,并在学校大力倡导信息技术与其他学科的深度融合,鼓励教师在教学中尽可能地为学生提供参与问题解决的各种机会和真实情境。并引导学生对遇到的问题提出不同的解决方案,让学生通过批判性的思考,从多种解决方案中找到最佳方案,进而提高学生的批判性思维和问题解决能力。
在生活环境方面,城市学生的计算思维及各维度能力均高于农村学生。这可能是城乡家庭之间具有一定的经济差距,每个家庭为学生提供的信息化设备和应用环境有所差距,影响了学生计算思维的发展;城市学校与农村学校在师资力量的配备、信息技术课程的开设、现代教育技术的应用、教育教学的理念和模式等方面都存在较大差距,这也是导致城市学生与农村学生计算思维水平存在显著差异的原因。从这些影响因素的分析中不难发现,学生初始的创造力并没有明显的差异,其他四个维度的能力更容易受后期学习环境的影响,这也启示教师在教学过程中要充分考虑这些因素,利用小组合作探究学习、生活化的项目场景、更合理的技术手段、先进的教育理念提高学生的计算思维能力,缩小城乡学生的差距。
