基于速度优化与粒子群优化算法的插电式燃料电池有轨电车能量管理策略*
2022-12-13张爱军方陆文胡后征
张爱军 方陆文 胡后征
(1. 中铁建云南投资有限公司, 650220, 昆明; 2. 中国铁建昆仑投资集团有限公司, 610040, 成都;3. 昆明理工大学, 650500, 昆明∥第一作者, 高级工程师)
插电式燃料电池有轨电车以其无接触网化、零CO2和其他有害气体排放低、能源效率高及噪声低等特点受到了交通运输行业的高度关注[1]。与传统的燃料电池有轨电车相比,搭载小型燃料电池堆和配备大容量动力电池的插电式燃料电池有轨电车由于初始成本低、动力系统动态响应好、系统运行效率高,更适合应用于公共交通市场[2]。
插电式燃料电池有轨电车中,燃料电池和动力电池单独或联合地驱动列车行驶。因此,如何分配两者的功率,设计合理的能量管理策略,成为了插电式燃料电池有轨电车节能的关键[3-4]。基于模糊控制的燃料电池有轨电车能量管理策略使得氢燃料电池工作在高效率区域,且动力电池荷电状态(SOC)维持在合理的范围之内[5]。燃料电池有轨电车的能量管理策略主要分为基于规则和基于优化两大类。基于规则的能量管理策略结构简单,适用于实时控制,但规则动态特性较差[6];基于优化的能量管理策略分为全局优化和瞬时优化,全局优化以动态规划(DP)最为典型,但必须以得知全局的工况信息为前提,难以实现在线应用[7-8]。文献[9]以混合储能有轨电车为研究目标,设计了基于粒子群优化(PSO)算法和庞特里亚金极小值原理(PMP)的能量管理策略。仿真结果表明,相比优化前的能量管理策略,优化后的控制策略下有轨电车的能耗降低8%左右。恰当的瞬时优化能量管理策略可以在线实现全局最优的燃油经济性,大量学者对此进行了广泛的研究[6, 10]。文献[11]提出了基于模型预测控制(MPC)的燃料电池有轨电车能量管理策略,并通过实车验证了所提策略的实时性和节能效果。
混合动力有轨电车能量管理高度依赖于速度规划。随着智能化交通系统的发展,列车与交通设施之间的通信(V2I)为插电式燃料电池有轨电车获得更优的经济车速提供了更大的可能性[12]。借助V2I获得的交通环境信息,优化有轨电车的速度轨迹以减少其急变速和怠速等行为,并结合动力系统能量管理优化策略,最终实现混合动力有轨电车的节能出行。本文提出了车联网环境下基于列车站台之间速度曲线优化的能量管理策略,基于伪谱法得到最优绿灯通行速度轨迹。采用PSO算法,对目标列车动力系统进行能量的优化分配,可有效提高列车的能耗经济性。
1 插电式燃料电池有轨电车模型的建立
1.1 插电式燃料电池有轨电车整车模型
本文选取插电式燃料电池有轨电车作为目标车辆。插电式燃料电池有轨电车的主要参数见表1,其动力系统简图见图1。

表1 插电式燃料电池有轨电车的主要参数
图1中,燃料电池作为主要的能量源,通过单向DC/DC转换器与母线连接;动力电池则作为辅助能源直接与母线相连,两者共同或单独驱动电机。动力电池与DC/AC转换器之间可以实现能量的双向流动,用于回收列车制动时的能量,并将能量储存至动力电池中。到站停车时,燃料电池还能为动力电池进行充电。
本研究中仅考虑纵向动力学。列车牵引力Ft应满足:
(1)
其中
(2)
式中:
m——列车质量,t;
g——重力加速度,m/s2;
i——道路坡度, ‰;
w0——列车基本阻力,N/kN;
md——包含回转质量在内的列车总质量, t;
γ——回旋质量系数;
v(t)——列车运行速度, km/h;
t——列车运行时间,min;
a、b、c——分别根据经验取值,本文选取a为2.59、b为0.091、c为0.000 775、γ为0.1。
列车需求功率Preq(t)可由式(3)计算得到:
(3)
式中:
ηDC, AC、ηM和ηT——分别为DC/AC转换器、驱动电机及传动系统的效率。
列车的功率平衡关系为:
Preq(t)=Pfc(t)ηDC,DC+Pbat
(4)
式中:
Pfc——燃料电池的功率;
Pbat——动力电池的功率;
ηDC,DC——DC/DC转换器的效率。
当车速已知时,根据式(4)确定Preq(t)。为方便计算,本文将DC/AC转换器、DC/DC转换器及传动系统的效率均取为0.9。采用恰当的能量管理策略对燃料电池系统和动力电池系统功率进行分配,以实现对列车经济性的优化。
1.2 燃料电池模型
燃料电池将化学能转化成电能,其H2的消耗率与功率有关,即:
(5)
式中:
ηfc、LHV——分别代表燃料电池的效率和低热值;
本研究中,为简化计算,不考虑燃料电池内部模型,只考虑燃料电池的功率输出,且燃料电池的最大输出功率选取为150 kW。
1.3 动力电池模型
在本文研究中,采用一种简单的等效电池模型来表达电池内部状态。电池内阻和开路电压的关系式为:
(6)
式中:
OCV——开路电压;
ibat——电流;
Rint——电池内阻;
Cbat——电池容量;
SOC,0——电池的初始荷电状态;
SOC(t)——每一时刻电池的荷电状态。
在该等效电路模型中,开路电压和内阻由电池SOC进行插值得到,如图2所示。
1.4 电机模型
本文对电机建模时,其主要参数见表2。不考虑电机瞬态响应的影响,将电机效率简化为电机转速和转矩相关的函数ηM(ωMG,TMG)。其中,ηM为电机效率,ωMG为电机转速,TMG为电机转矩。

表2 电机的主要参数
电机效率随其转速和扭矩变化曲线见图3。
由图3可见,电机的效率与电机的转速和转矩相关。根据图3中的电机效率分布,为方便本文计算,取电机效率为0.85。
基于上述建立的列车整车和动力系统模型,本文提出了基于速度优化的有轨电车能量管理策略,以实现目标列车燃油经济性的优化。对列车速度优化的范围为两个相邻的站点,且站点之间存在一个红绿灯,其相位和时长可通过V2I获取。在求解列车的经济车速时,需考虑红绿灯对其能耗的影响。
2 红绿灯对列车速度优化的影响

(7)
式中:
Jv——列车的能耗;
Pt——列车的功率;
x0、xtf1、xtf——分别为列车初始时刻、tf1、tf时的状态变量;
amin、amax——分别为列车的最小和最大的速度;
vmin、vmax——分别为列车的最小和最大速度;
sstation——下一个站点的位置,取 2 000 m;
tf——到达下一个站点的时间,取 120 s;
slight——红绿灯位置,取1 000 m;
tf1和vtar——分别表示到达红、绿灯的时间和速度,可通过式(8)求解获得。
(8)
式中:
vlow、vhigh——分别为有轨电车在绿灯相位下不停车通过交叉口的最小和最大速度;
tr和tg——分别代表下一个红灯和绿灯的开始时刻。
本文采用Radau伪谱法求解上述目标函数,以获取两个站点之间列车的最优速度。
3 基于速度优化与PSO算法的有轨电车能量管理策略
本文通过考虑两个站点间红绿灯的影响,得到目标列车的最优速度轨迹。基于此最优速度轨迹,建立基于PSO算法的有轨电车能量管理策略,从而对目标列车燃料电池和动力电池的功率进行优化分配,以实现整车燃油经济性的提高。
对于该能量管理策略,选取SOC作为状态变量,表示为x,即x=SOC;选取燃料电池功率作为控制变量,表示为u,即u=Pfc。将燃料电池H2消耗和动力电池等效H2消耗的总和作为优化目标函数Je。同时,为了将动力电池SOC控制在正常范围内,在优化目标函数中引入调节系数ξ,如式(9)所示:
(9)
式中:
Je——列车的最小能耗;
SOC,min、SOC,max——分别为电池最小和最大的荷电状态。
同时,为了保护有轨电车能量分配中的各个部件,考虑到各个部件的功率限制和性能要求,需满足式(10)的约束:
(10)
式中:
Pfc,min、Pfc,max——分别为燃料电池的最小和最大功率;
Pbat,min、Pbat,max——分别为动力电池的最小和最大功率;
Pmot(t)——电机功率;
Pmot,min、Pmot,max——分别为电机的最小和最大功率。
采用PSO算法,求解上述目标函数,得到最优的燃料电池功率,实现动力系统能量的优化分配。
4 基于速度优化的有轨电车能量管理仿真分析
4.1 有轨电车速度优化结果分析
对列车速度优化算法进行验证和分析。图4描述了两个站点之间列车的速度和距离。由图4可见,列车呈现“加速-巡航-减速”的行驶模式。为了在绿灯窗口内通过路口,列车进行了平缓的减速。列车顺利通行之后,先加速后减速,最终在要求的到站时刻减速停车至下一个站点。上述结果验证了本文所提速度优化策略的可行性,其能保证列车在绿灯窗口内通过路口,并在规定的时刻到达站点。
4.2 有轨电车能量管理策略优化前后结果分析
为了验证所提有轨电车能量管理策略在长工况下的节能效果,将上述两个站点之间的速度组合为长工况。基于长工况,将所提策略与基于规则的有轨电车能量管理策略进行对比和分析。基于规则的有轨电车能量管理策略根据动力电池的SOC来决定燃料电池的输出功率。图5—图6给出了在验证工况下,动力电池SOC、燃料电池H2消耗、燃料电池输出功率和动力电池输出功率在基于速度优化与规则的有轨电车能量管理策略和基于速度优化与PSO算法的有轨电车能量管理策略的变化对比。由图5—图6可见,基于规则的有轨电车能量管理策略在初始阶段主要使用动力电池作为能量源,因此SOC下降迅速,此时的H2消耗低于基于PSO算法的有轨电车能量管理策略的H2消耗。但当SOC下降至0.3后,为了使SOC维持在这一稳定的状态,基于规则的有轨电车能量管理策略使用燃料电池作为主要的能量源并为动力电池充电,此时的H2消耗快速上升并超过了基于PSO算法的有轨电车能量管理策略。经PSO算法优化后,列车动力电池SOC下降缓慢,接近最优的线性变化趋势,且最终的H2消耗低于基于规则的有轨电车能量管理策略下的H2消耗。
表3给出了两种策略下的动力电池SOC始末值、燃料电池H2消耗及燃料电池的经济性改善比例。综上分析,本文所提的基于PSO的能量优化策略可以更加合理地分配燃料电池和动力电池的功率,最终使列车的经济性提高了3.72%。
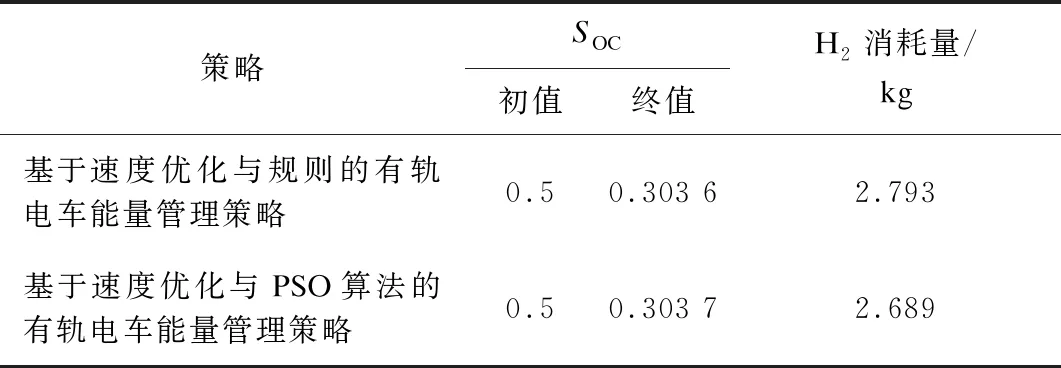
表3 有轨电车能量管理策略优化前后效果对比
5 结语
本文以优化燃料电池有轨电车的能耗经济性为目标,建立了车联网环境下的分层控制框架。上层考虑信号交叉口的影响,将红绿灯的相位和配时转化成终端时刻约束,建立以驱动能耗最小为目标的最优控制框架,并采用伪谱法求解获得最优车速。基于该最优车速,下层建立了基于PSO算法的燃料电池有轨电车能量管理策略,对其动力系统中动力电池和燃料电池功率进行了优化分配。仿真结果验证了所提算法的有效性,保证了列车平缓地在绿灯窗口内通过路口,且相比传统基于规则的有轨电车能量管理策略,列车在基于PSO算法的有轨电车能量管理策略下能耗降低了3.72%。本文只考虑了燃料电池有轨电车在两站台且仅含单个红绿灯轨道上行驶的情况,后续将进一步研究在多站台且含多个红绿灯轨道上的行驶情况。
