基于自回归滑动平均模型的大口径天线风速预测方法*
2022-12-12王文娟连培园王从思何飞龙
李 琳 许 谦 王文娟 李 帅 薛 松 连培园 王从思 何飞龙
(1 新疆大学物理科学与技术学院乌 鲁木齐 830046)(2 中国科学院新疆天文台 乌鲁木齐 830011)(3 中国科学院射电天文重点实验室 乌鲁木齐 830011)(4 新疆射电天体物理重点实验室 乌鲁木齐 830011)(5 西安电子科技大学电子装备结构设计教育部重点实验室 西安 710071)(6 中国科学院大学 北京 100049)
1 引言
大型反射面天线具有高增益、窄波束的特点,被广泛应用于射电天文、深空探测等领域[1].随着引力波探测、恒星形成、星系起源等科学研究的深入,需要进一步提高天线的增益和分辨率,为此需要增大口径或提升工作频段[2].但是天线口径增大会导致天线波束变窄,从而对天线指向精度提出更苛刻的要求.例如我国即将建造的新疆奇台110 m口径全向可动射电望远镜(QiTai Telescope,QTT),为满足科学目标需求,当其工作频率为115 GHz时,指向精度要达到1.5′′(0.000416°)[3].对于大口径天线而言,其工作往往处于露天环境中,面临重力、风扰、温差、积雪等环境载荷导致指向精度下降的问题,尤其是具有随机性和时变性的风扰,是环境载荷中最复杂的问题之一[4–5].
国内外许多学者已经发现风扰对天线指向精度的影响.西安电子科技大学Duan等人利用数值分析对7.3 m天线变形引起的指向误差进行研究,得到天线仰角为0°时,方位轴受到静载引起指向误差为0.0001°,当天线受到20 m·s-1的静态风载时,其指向误差增大为0.0135°[6].美国国家航天局通过对天线伺服系统建模,将风扰动作为干扰力矩进行分析,发现当平均风速为3.47 m·s-1时,编码器检测到34 m天线的指向误差为0.00048°,70 m天线的指向误差为0.0013°[7–8].日本国立天文台研究风致10 m天线指向误差,得到在10 m·s-1的风速下,10 m天线的指向误差达到0.00047°[9].
为降低风扰对天线指向的影响,国内外学者往往采用天线罩、增强天线结构刚度和强度等手段降低天线结构变形,或者通过优化伺服控制器以增强控制系统鲁棒性[9]以及利用固定补偿等方法降低风扰对天线指向的影响.虽然使用天线罩能降低风扰对天线的影响,但制作天线罩的材料会吸收或反射电磁波而降低天线电性能.且天线罩制作、运输安装难度随口径增大而急剧增加,仅适用于小口径天线.伺服控制补偿都是针对静态载荷导致的天线变形或振动.对于时变的风载影响,利用风预测提前得到作用在天线上的风速,为控制系统的计算和执行提供足够时间,才能更好地降低天线在风扰下执行观测任务时风载荷导致的指向抖动.
在风预测领域,Brown等[10]利用自回归模型(Autoregressive,AR)考虑了太平洋西北地区某风场数据的非高斯平稳性和昼夜非平稳性,采用幂变换和标准化进行了建模预测.采用AR(2)模型,Poggi等[11]对法国科西地区的风速数据进行了仿真与预测,结果表明,AR(2)模型能够很好地复现原始序列,反映风场数据的统计特性.丁明等[12]采用自回归滑动平均模型(Autoregressive Moving Average Model,ARMA)对风速进行预测,比较了预测风速和实际风速的分布特性.研究重点关注如何使用时间序列模型模拟风速序列,使其具有风的一般特征,尽管这些模型都涉及到风预测,但在实际预测中,并没有使用单独预测集来验证模型的预测性能.即以上使用滑动自回归模型研究的重点是模型在训练数据上的逼近能力,而非模型预测能力.
本研究以QTT台址的风速预测为目标,通过采集QTT台址风场数据分析台址风场特征,并将不同季度的风场数据划分为训练集和测试集.通过对不同季度训练集数据进行建模,即在训练集数据平稳性检验、模型定阶、参数估计、残差检验的基础上,建立ARMA模型进行风预测,获取台址风速预测值,与测试值比较计算预测精度.
2 台址风特性分析
QTT台址位于新疆昌吉自治州奇台县半截沟镇石河子村,台址海拔约1730–1830 m,位于东天山北麓一处南北约2 km、东西约1.5 km且四面环山的矩形盆地[3].台址特征是盆地东南高西北低,西侧是落差在110 m左右的中葛根河谷,四周分布的山体海拔高度约为1860–2250 m.台址内已建一个60 m高的梯度风塔,台址地形和测风塔的位置如图1所示,图中线框所围区域为QTT台址园区,F为测风塔位置,T为QTT位置[13].

图1 QTT射电望远镜与测风塔位置.(a)测风塔;(b)QTT天线.Fig.1 QTT site and position of anemometer tower.(a)anemometer tower;(b)QTT antenna.
风塔数据采集设备包括2D超声波风速风向传感器和CR3000微型采集器,风塔采集频率为每分钟1次,采集时长为1 s[13],这样按照一定时间间隔采集和记录的风数据构成台址风场的时间序列,该时间序列包含产生该序列系统的历史行为全部信息.研究所用数据为在QTT台址利用测风塔采集的2017年4–12月10 m高度的风数据.通过对4–12月风速时间序列中不同风速出现的频率分析,得出如图2所示台址风速概率分布图以及图3所示风速风向玫瑰图.在图2风速概率分布图中可以看出在2017年4–12月台址风速集中在1–8 m·s-1的范围.

图2 台址2017年4–12月风速概率分布图.(a)时间序列中提取的分布;(b)时间序列中提取的累积分布.Fig.2 Probability distribution of wind speed from April to December 2017 of QTT site.(a)Distribution extracted from the time series;(b)Cumulative distribution extracted from the time series.
在图3风速风向玫瑰图中,每个扇形所指方向表示从外部吹向测风塔的风向,扇形上不同的灰度代表不同风速.例如正南方向的扇形数据显示,正南方向0–2 m·s-1风速所占时间约为6%,2–4 m·s-1风速所占时间约为2%,4–6 m·s-1风速所占时间约为1.5%,6–8 m·s-1风速所占时间约为1%,8–10 m·s-1、10–12 m·s-1风速所占时间均小于1%.从图3风速风向玫瑰图还可以得出QTT台址风在西南、南、东南和西北4个风向出现较多,且高风速在西南风向出现频次更高.

图3 台址2017年4–12月风速风向玫瑰图Fig.3 Wind rose diagram from April to December 2017 of QTT site
为观察台址风数据在不同季度的差异,本研究按照传统四季分布即4、5、6月为夏季,7、8、9月为秋季,10、11、12月为冬季,得到3个季度的风玫瑰图,如图4所示.从3个季度的风玫瑰图可得出风向多集中于南、北两个风向,相较于南向的风,在北向风中4–6 m·s-1风速所占时间较多,但大于6 m·s-1的风速多集中于南向风.夏秋两个季度风速风向特征变化并不明显,冬季台址的风向多集中在东南偏南方向,大于6 m·s-1的风速基本不出现.3个季度的风玫瑰图对比来看,QTT台址的风场数据具有明显季节差异,应按照不同季度数据建立不同风预测模型.

图4 不同季度的风速风向玫瑰图.(a)夏季风玫瑰图;(b)秋季风玫瑰图;(c)冬季风玫瑰图.Fig.4 Wind rose diagram of different quarters.(a)Wind rose diagram in summer;(b)Wind rose diagram in autumn;(c)Wind rose diagram in winter.
3 基于ARMA模型的风速预测方法
根据预测的时间尺度不同,风预测可分为超短期预测、短期预测、中期预测和长期预测[14–15].把提前几分钟至30 min左右的预测定义为超短期预测,而短期预测则是指提前30 min至72 h左右的预测,而把提前几天或数周、数月的预测称之为中期预测,长期预测是以年为预测单位.对于望远镜来说,短期预测可以给望远镜观测任务的规划提供参考,超短期预测可以给望远镜伺服控制提供输入数据,为控制系统的运动机构争取执行时间,在风作用到望远镜时完成姿态调整.以输入数据分类风预测主要包括物理方法和统计方法.物理方法的输入数据通常为各种物理描述量,包括地形地貌特征、气象信息、地表粗糙度、障碍物等地理信息.其优点是不会过度依赖风历史数据,且考虑了气象、地理等复杂物理量,可获得较精确的中长期预测值,缺点是需要建立精确的地理模型,且计算也十分复杂,需借助超算才可能实现.统计方法则是将风场历史数据作为输入数据,通过提取历史数据中的输入输出映射关系构建统计模型,从而对将来的风速进行预测.其优点是不考虑风速产生的复杂物理过程,计算简单[16].故本研究采用统计方法预测超短期风速.
3.1 时间序列模型
经典时间序列模型包括:自回归模型、滑动平均(MA)模型以及自回归滑动平均模型3种.时间序列模型的建模步骤主要包括模型阶次辨识、参数估计与诊断.
(1)AR模型
AR模型的基本思想是当前风速值xt可以通过p个自身的过去值xt-1,xt-2,···,xt-p来解释.其中p表示预测当前值所需要的历史步长,该模型假定序列当前值是过去值的线性函数.阶数为p的AR模型,一般记作AR(p),数学表达式为:

式中φ1,φ2,···,φp是自回归系数,εt是白噪声序列.
(2)MA模型
白噪声的线性组合构成了MA模型假设序列,通常来说,阶数为q的MA模型,记作MA(q),其数学表达式为:

式中,θ1,θ2,···,θq是滑动平均系数.
(3)ARMA模型
ARMA模型假设序列的当前值由其过去值和系统噪声的过去值线性组合而成,即时间序列的当前值,其不仅取决于过去某一特定时间内的历史数据,还取决于当前和过去时刻引入系统中的噪声.ARMA(p,q)的数学表达式为:

其中,p、q分别为自回归阶数和滑动平均阶数.当q=0时,ARMA(p,q)模型转变为AR(p)模型;当p=0时,ARMA(p,q)模型转变为MA(q)模型.
3.2 预测模型的构建
ARMA模型要求风速数据{xt}为平稳、正态、零均值的时间序列,因此在建模之前需要对数据进行预处理,从而得到符合要求的风速时间序列.由图2可以看出台址的风速不具有正态分布特性,但ARMA模型预测主要是利用风速数据的相关性,要求风速时间序列的基本特性不变,对其正态分布特性要求不严格,本文不再对风速数据进行正态化处理,这里只需要对时间序列进行差分处理和零均值标准化处理.但要注意不能过度差分,否则会导致时间序列的方差增大.
(1)风速时间序列的预处理
为验证预测效果,本研究将每个季度风速时间序列分为95%的训练集和5%的测试集.即利用一个季度2052 h的风速数据预测108 h的风速数据,然后将预测数据与测试集数据进行对比验证.3个季度训练集风速数据如图5所示,训练集风速时间序列的自相关函数和偏自相关函数如图6所示,其中自相关函数(Autocorrelation Function,ACF)是表示当前时刻的数值与过去时刻的数值之间的相关程度,包括直接和间接的相关性信息;偏自相关函数(Partial Autocorrelation Function,PACF)是表示当前时刻的数值与过去时刻的数值的直接相关程度.相关函数中自相关系数随滞后值的增加迅速衰减为零的时间序列是平稳序列,反之是非平稳序列.由于ARMA模型要求时间序列数据必须平稳,因此本研究利用ADF(Augmented Dickey-Fuller Test)检验和KPSS(Kwiatkowski-Phillips-Schmidt-Shin Test)检验等单位根检验方法确定训练集风速时间序列的平稳性,自相关函数中相关系数是否衰减为零也可以作为判断时间序列是否平稳的依据,可以与单位根检验平稳性的方法相互验证,增加平稳性检验的准确性.

图5 不同季度的训练集风速时间序列图.(a)夏季;(b)秋季;(c)冬季.Fig.5 Wind speed time series of training set in different quarters.(a)Summer;(b)Autumn;(c)Winter.
图6中自相关系数没有随着滞后值迅速衰减至0,因此可以判定该时序数据属于非平稳序列,需要对训练集数据进行一阶差分,差分公式为Δxt=xt+1-xt,差分后每个季度风数据时间序列的自相关函数和偏自相关函数如图7所示.可以得到每个季度自相关系数随着滞后值增加很快衰减至0,判断3个季度风速时间序列属于平稳序列,故而不再进行差分.

图6 训练集风速时间序列相关函数.(a)夏季自相关函数;(b)夏季偏自相关函数;(c)秋季自相关函数;(d)秋季偏自相关函数;(e)冬季自相关函数;(f)冬季偏自相关函数.Fig.6 Correlation function of wind speed time series of training set.(a)Autocorrelation function in summer;(b)Partial autocorrelation function in summer;(c)Autocorrelation function in autumn;(d)Partial autocorrelation function in autumn;(e)Autocorrelation function in winter;(f)Partial autocorrelation function in winter.

图7 差分后训练集风速时间序列相关函数.(a)夏季自相关函数;(b)夏季偏自相关函数;(c)秋季自相关函数;(d)秋季偏自相关函数;(e)冬季自相关函数;(f)冬季偏自相关函数.Fig.7 Correlation function of wind speed time series of training set after difference.(a)Autocorrelation function in summer;(b)Partial autocorrelation function in summer;(c)Autocorrelation function in autumn;(d)Partial autocorrelation function in autumn;(e)Autocorrelation function in winter;(f)Partial autocorrelation function in winter.
(2)模型识别
模型识别包括类别判断与阶数选取,通常通过风速数据中相关函数的自相关性进行模型类别判断,但实际时间序列数据具有很强的随机性,序列中会随机出现异常值波动从而导致相关系数的截尾性不明显,所以常利用准则函数进行模型阶数选取.常用的准则函数是基于信息论的赤池信息准则(Akaike Information Criterion,AIC)[17]和贝叶斯信息准则(Bayesian Information Criterion,BIC)[18],通过如下公式计算每个模型的AIC值或BIC值:
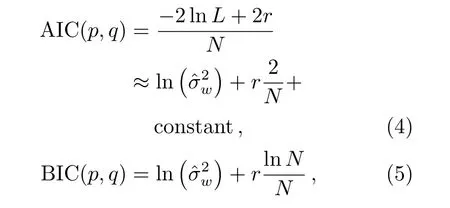
式中,L是模型的似然函数,N是序列的长度,w是噪声误差的参数,ˆσ2w是噪声误差的最大似然估计,r=p+q+1表示模型中待估计参数的数目.AIC和BIC准则的表达式均由两项组成,第1项表示模型的拟合程度,一般模型的阶次越大其值越小;第2项表示对过多参数的惩罚,模型阶次越大其值越大.对各种可能的模型,具有最小值的AIC或BIC即为最终选定的模型,每个季度的不同阶数预测模型的AIC和BIC值如图8所示,每个灰度格子的数值对应不同阶数的AIC和BIC值之和,该数值结果越小说明模型越优异,从而确定预测模型的阶数.其中夏季最佳预测模型为ARMA(5,5),秋季的最佳预测模型为ARMA(5,4),冬季的最佳预测模型为ARMA(3,5).

图8 不同季度风速预测模型的最优阶数.(a)夏季ARMA模型的最优阶数是(5,5);(b)秋季ARMA模型的最优阶数是(5,4);(c)冬季ARMA模型的最优阶数是(3,5).Fig.8 Optimal order of wind speed prediction model in different quarters.(a)The optimal order of summer ARMA model is(5,5);(b)The optimal order of autumn ARMA model is(5,4);(c)The optimal order of winter ARMA model is(3,5).
(3)模型参数估计
模型阶次确定后,可以根据风速时间序列x1,x2,···,xt进行参数估计,得到φ1,φ2,···,φp和ε1,ε2,···,εq的估计值.常用的估计方法如:矩估计、最小二乘估计和最大似然估计.矩估计是让样本矩和相应的理论矩相等,通过求解方程组得到未知参数的估计,对于ARMA模型而言,矩估计计算复杂且无法得到最优估计.最小二乘估计基于误差平方和最小原则得到参数估计值,当时间序列数据数目较大时,使用一些初始值对最终的参数估计影响不大,数目较少时,采用无条件最小二乘或最大似然进行参数估计.最大似然估计通过选取模型参数使得似然函数最大化,似然函数是模型参数的函数,代表了时间序列值出现的可能性.本研究利用estimate函数对3个季度定阶的模型进行最大似然估计,分别得到以下模型:
summer:
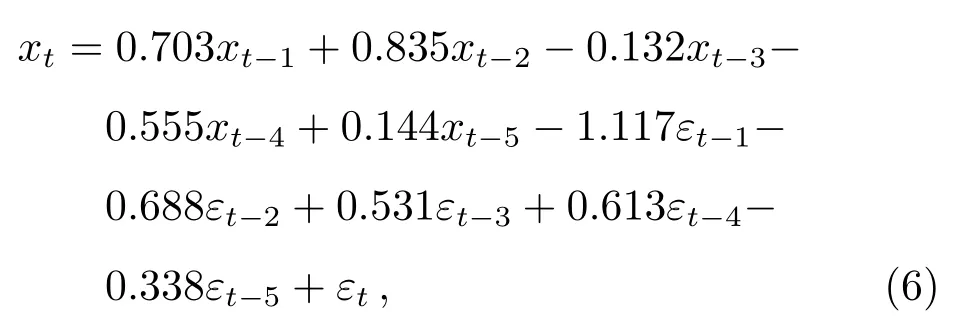
autumn:

winter:

(4)模型诊断检验
经过阶次辨识和参数估计得到的模型,需要进行残差分析.如果分析结果较差,需要重新进入“辨识-估计-诊断”的流程.对于残差分析,残差正态分布的检验通过判断直方图或分位数-分位数(Quantile-Quantile,Q-Q)图中模型的残差分布与标准正态分布的拟合程度来实现;残差随机性检验通过判断样本自相关函数和偏自相关函数中相关系数是否满足截尾来实现.
图9展现了夏季ARMA模型的残差检验,图9(a)是对夏季模型残差进行标准化处理,得到了零均值且方差为一的标准化残差序列;图9(b)是对标准化残差序列求得残差的数值分布,分布呈现正态分布,说明满足残差检验的正态分布;图9(c)中可以看出代表模型残差分布的十字标与代表标准正态分布的虚线拟合效果较好,模型满足残差检验的正态分布;图9(d)自相关函数和图9(e)偏自相关函数中,点表示对应滞后值的自相关系数或偏自相关系数,线表示自相关系数或偏自相关系数满足相关性截尾的95%置信区间上下限,可以看出相关系数在95%置信区间下满足趋近于零的条件,由此说明残差序列无明显相关性且随机性强,模型满足残差检验的随机性.夏季ARMA模型满足模型残差检验的要求,模型的残差序列是白噪声信号,原始风速序列中有用信息已被提取到预测模型中.图10展现了秋季ARMA模型的残差检验,图11展现了冬季ARMA模型的残差检验,从图10和图11中可以看出秋季模型和冬季模型残差也是随机正态分布且不自相关.所以,可以判定3个季度模型类别和阶数选用合适.
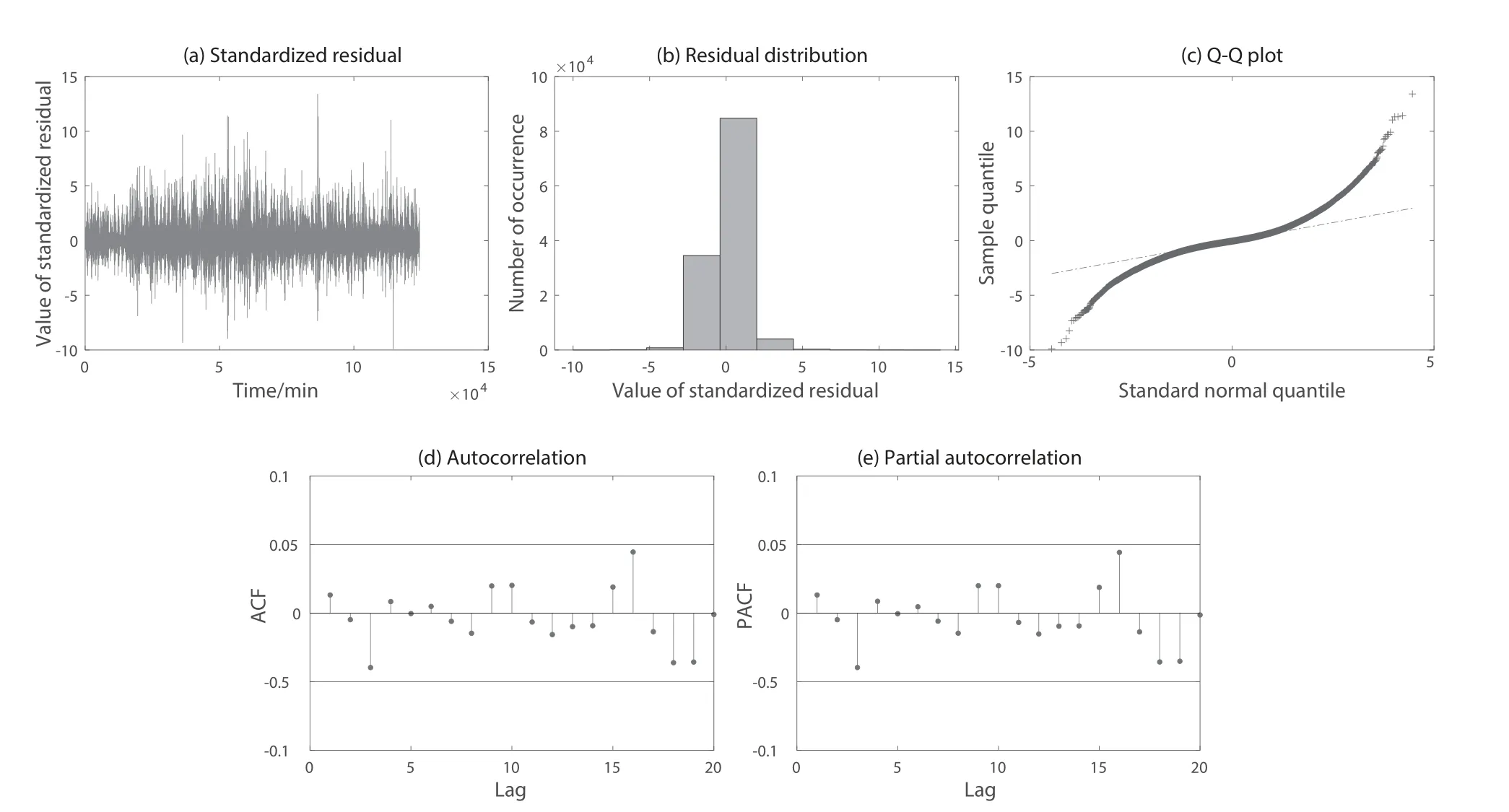
图9 夏季ARMA模型残差检验.(a)标准化残差;(b)残差分布;(c)Q-Q图;(d)自相关函数;(e)偏自相关函数.从图(b)中可以看出模型满足残差检验的正态分布;从图(c)中可以看出模型的残差分布拟合标准正态化分布效果较好;图(d)自相关函数和图(e)偏自相关函数中相关系数在95%置信区间下满足趋近于零的条件,说明残差序列无明显相关性且随机性强,模型满足残差检验的随机性.Fig.9 Residual test of ARMA model in summer.(a)Standardized residual;(b)Residual distribution;(c)Q-Q plot;(d)Autocorrelation function;(e)Partial autocorrelation function.It can be seen from panel(b)that the model satisfies the normal distribution of residual test;It can be seen from panel(c)that the residual distribution of the model fits the standard normal distribution well.The correlation coefficient in the ACF of panel(d)and PACF of panel(e)satisfies the condition of approaching zero under the 95% confidence interval,indicating that the residual sequence has no obvious correlation and strong randomness,and the model satisfies the randomness of the residual test.

图10 秋季ARMA模型残差检验.(a)标准化残差;(b)残差分布;(c)Q-Q图;(d)自相关函数;(e)偏自相关函数.Fig.10 Residual test of ARMA model in autumn:(a)Standardized residual;(b)Residual distribution;(c)Q-Q plot;(d)Autocorrelation function;(e)Partial autocorrelation function.
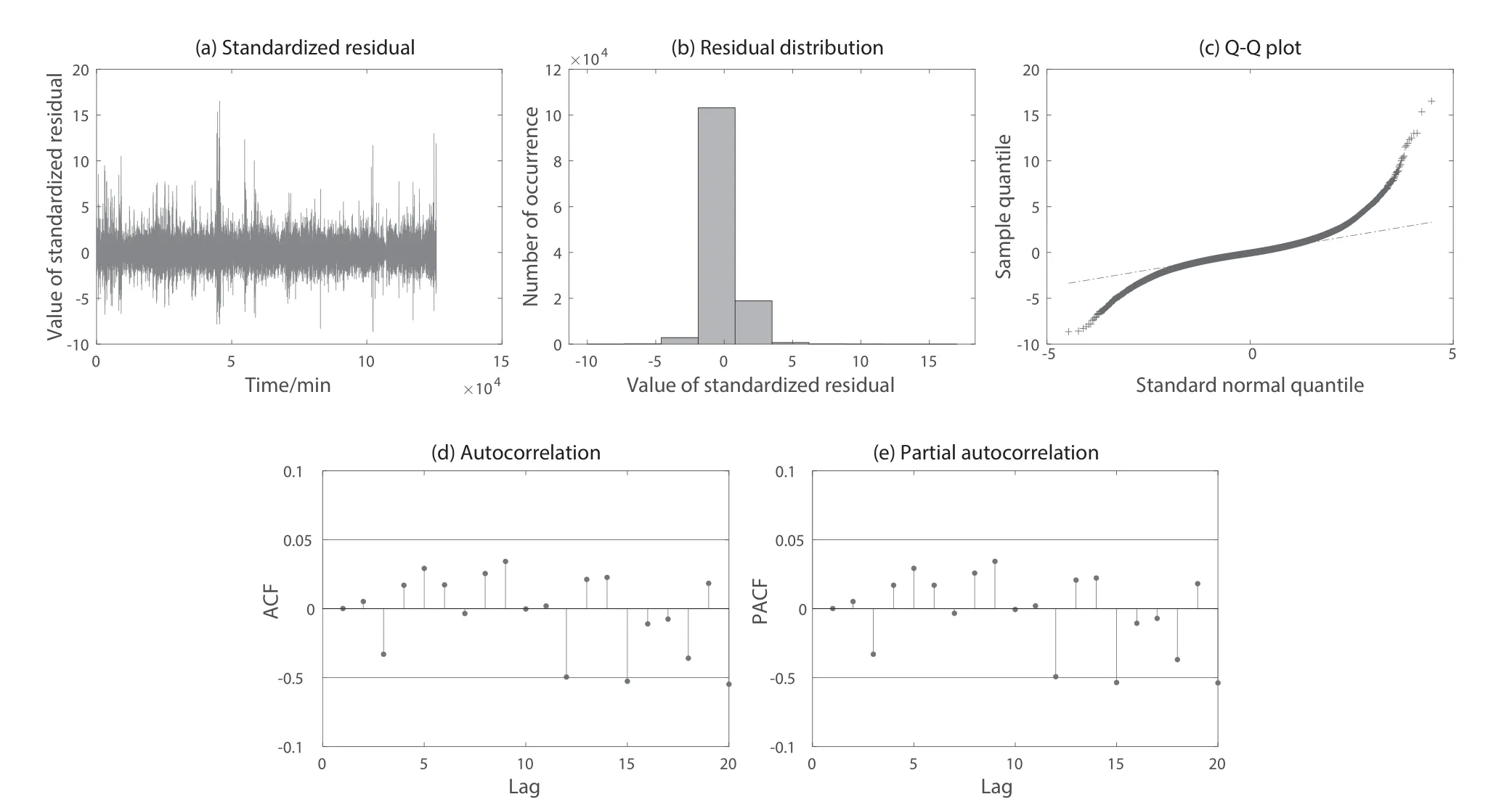
图11 冬季ARMA模型残差检验.(a)标准化残差;(b)残差分布;(c)Q-Q图;(d)自相关函数;(e)偏自相关函数.Fig.11 Residual test of ARMA model in winter.(a)Standardized residual;(b)Residual distribution;(c)Q-Q plot;(d)Autocorrelation function;(e)Partial autocorrelation function.
4 预测结果及分析
利用提出的不同季度ARMA模型进行预测,给出95%置信区间得到预测数据.图12显示了3个季度的预测值与测试值的对比图,图中灰色线代表训练集数据,点线代表测试集数据,黑线代表模型预测值,可得ARMA模型能够很好预测风速.图13选取3个季度部分预测值与测试值,点线为测试值,黑线为预测值,能清晰看出预测值与测试值的吻合程度,证明本研究建立的不同季度ARMA模型能够很好拟合真实值,预测精度较高.但模型对拐点处的值预测还不够准确,还存在一定误差,预测也存在一定滞后现象.
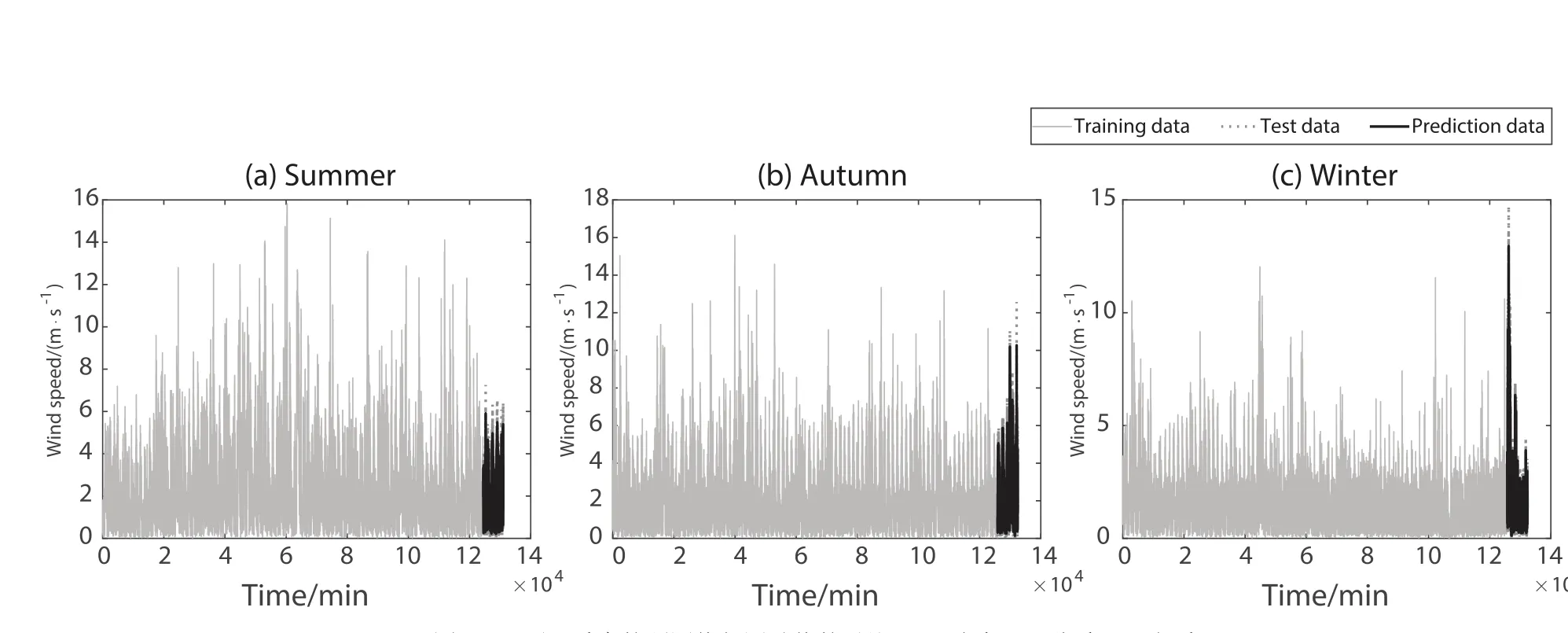
图12 不同季度的预测值与测试值的对比.(a)夏季;(b)秋季;(c)冬季.Fig.12 Comparison of prediction data and test data in different quarters.(a)Summer;(b)Autumn;(c)Winter.
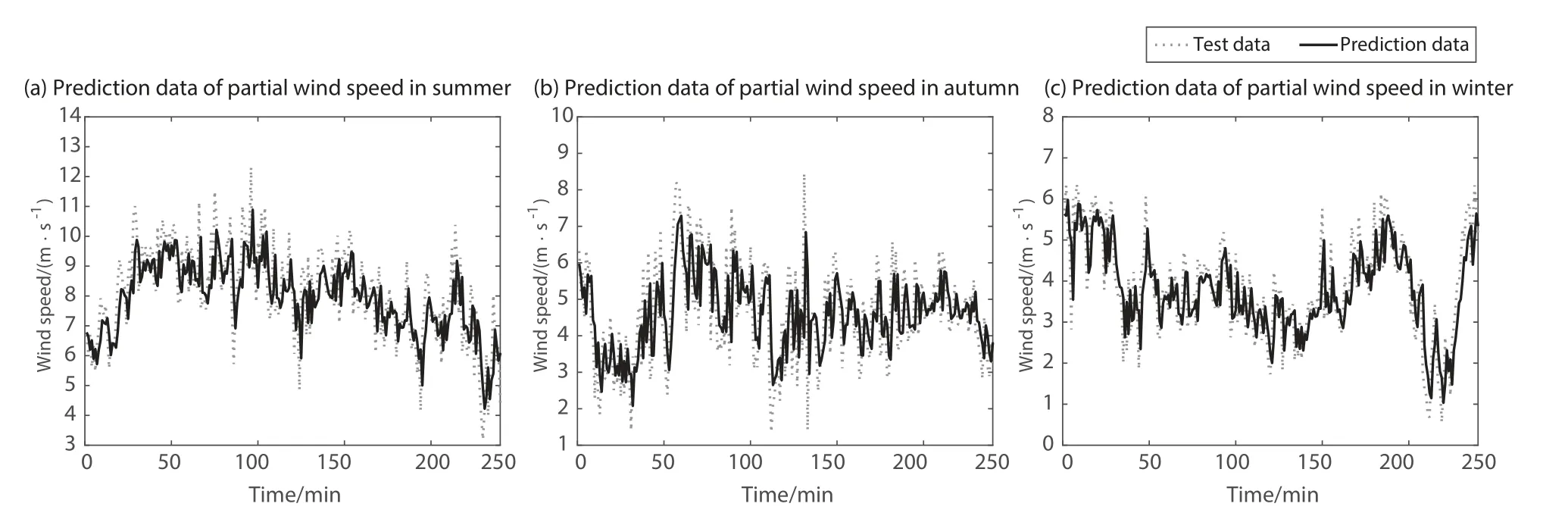
图13 不同季度的部分预测值与测试值的对比.(a)夏季部分风速预测值;(b)秋季部分风速预测值;(c)冬季部分风速预测值.Fig.13 Comparison of prediction data and test data in different quarters:(a)Prediction data of partial wind speed in summer;(b)Prediction data of partial wind speed in autumn;(c)Prediction data of partial wind speed in winter.
为定量比较预测精度,使用均方根误差(Root Mean Square Error,RMSE)、平均绝对误差(Mean Absolute Error,MAE)与平均绝对百分误差(Mean Absolute Percentage Error,MAPE)衡量预测值与测试值之间偏差,这3个指标取值越小代表预测精度越高,他们被广泛用于风速预测领域[19–20].其定义如下:

式中yi和ˆyi分别表示第i时刻风速观测值和预测值.
本文先预测30 min风速数据,将其加入训练集再预测下一个30 min的风速数据,经过多次滚动预测,从而实现108 h风速数据预测.由于误差随时间累积,我们发现4 h后预测数据误差较大,对望远镜控制执行时间来说,4 h完全能够满足,因此选择3个季度预测前4 h风速预测值与测试值的偏差衡量模型精度,结果如表1所示.

表1 不同季度ARMA模型预测效果Table 1 Prediction effect of ARMA model in different quarters
从不同季度ARMA模型预测效果来看,夏季平均绝对误差最小,平均绝对百分误差最大,这是由于夏季的测试集前4 h的平均风速较冬季和秋季小.整体来看,3个季度预测效果较为接近,秋季风速预测精度最高.
为比较本文风速预测精度的优劣,将本文3个季度模型误差值取平均,并选取3篇文献的风速预测精度作为参考.其中Jiang等[21]对山东蓬莱某风电场的风速进行了预测,Song等[22]对中国某风电场的风速短期预测进行了研究,Zhang等[23]对西班牙某风电场的风速进行了预测,以上文献中风速预测精度与本文风速预测精度如表2所示.可以看出本文风速预测的平均绝对误差和均方根误差均优于以上文献.本文的风速预测模型具有一定的优越性.

表2 本文风速预测精度与其他文献中风速预测精度比较Table 2 The accuracy comparison of wind prediction between this article and other work
在时间尺度上,4 h范围的风预测数据能够为射电望远镜控制系统运动机构提供足够的执行时间,并且能指导射电望远镜在此段时间观测任务的安排.故本研究基于不同季度风速数据建立的ARMA模型能够很好地预测台址风速,为射电望远镜的抗风扰控制提供必要数据支撑.
5 结论
风因其间歇性、波动性以及随机性等特点,给大口径射电望远镜的抗风扰控制补偿带来严峻挑战,克服这一难题的有效途径是对台址风场进行预测.本研究根据台址风塔采集到2017年4-12月风速风向数据,分析了台址风场特征,发现不同季度风速风向有较大差异.在此基础上通过对不同季度风速数据的平稳性检验和数据处理,利用AIC准则确定模型阶数,最大似然法估算模型参数,最终建立了不同季度的ARMA模型,并进行了风速预测,从均方根误差、平均绝对误差与平均绝对百分误差的值来看,风速预测取得很好的效果,能够满足大口径射电望远镜抗风扰控制在大多数情况下的使用.
在风速变化较大的拐点处,本研究建立的风速预测模型预测精度不够高,随着预测时间的增加,预测精度也逐渐变低,因此未来还需要对算法进行优化.另外,由于本研究采用统计预测方法,仅利用风速历史数据进行建模预测,预测效果有限.因此与数值天气预报有限结合,进一步提升预测精度是未来研究的一个重点.
台址风场的风速预测不是最终目的,如何利用预测结果和大口径射电望远镜主副伺服控制系统建立联系,共同保障风扰下射电望远镜的观测性能,是下一步的研究工作.
