日月轨道计算对TLE深空编目目标预报精度的影响*

郭效忠 李佳威 沈 鸣 高鹏骐 杨大陶 于欢欢 赵 有

(1 中国科学院国家天文台 北京 100101)(2 中国科学院大学 北京 100049)(3 探月与航天工程中心 北京 100190)

1 引言

双行根数(Two Line Element,TLE)编目是以SGP4(Simplified General Perturbations 4)力学模型为基础的轨道确定结果,由美国SSN(Space Surveillance Network)提供观测数据支持.依赖于美国SSN的强大观测能力和全球站点分布,TLE编目可以实现大部分空间物体的日更新.通常认为,TLE编目具有公里级定轨精度,可以编目管理直径大于10 cm的低轨道空间物体和直径大于1 m的地球同步轨道空间物体.作为一种可公开获取的近地空间物体数据,TLE编目在空间物体观测[1–2]、空间物体交会筛查和碰撞概率计算[3]、太空态势感知[4–6]等多个研究领域都有应用.由于TLE编目对空间物体的覆盖范围广,其在碰撞风险评估过程中有着重要作用.

随着空间编目数量的不断增多,如何保障在轨航天器的运行安全及合理地进行空间物体碰撞风险评估,成为所有航天活动参与者都要面对的重要问题.这其中,基于碰撞概率计算[7–9]的空间物体预警规避方法,成为一种可定量描述潜在风险、辅助决策机动方案的有效方法.准确、有效的碰撞概率计算依赖于交会事件中主从目标的精确轨道预报,包括二者位置、速度和协方差矩阵的结果.美国国家航空航天局(NASA)指出,将TLE编目数据直接应用于空间物体碰撞概率计算,其精度是无法满足规避决策需求的1https://satellitesafety.gsfc.nasa.gov/CARA.html..

针对TLE编目预报精度的评估和改进问题,国内外学者已开展多方面的研究.韦栋等[10–11]以建立数值参考轨道的方式,给出了几类典型轨道的TLE定轨和预报精度评估统计结果.Coughlin[12]用类似方法研究了EGP(Enhanced General Perturbation)方式生成TLE数据的预报精度.Kelso[13]则以GPS星历为基准,发现TLE编目可能存在明显的偏差.利用稀疏光学观测资料,赵广宇等[14]实现了对TLE编目的改进,可以提高其预报3 d、7 d时长的精度.刘卫等[15]和Vallado等[16]则以历史TLE编目作为“观测数据”,考虑更加完整的力学模型进行“二次”定轨以实现预报精度的改进.Li等[17]和Curzi等[18]验证了机器学习和神经网络在预测TLE编目预报误差模式的有效性,并采用模型补偿方式提高预报准确性.针对SGP4模型的限制,许晓丽等[19]指出缺少J22田谐项摄动,使得TLE编目存在无法消除的周期性系统误差,对于500 km高度的低轨卫星会达到千米量级.

由美国太空军下属机构Space Operations Command所主导的Astrodynamics Standards2https://www.space-track.org/documentation#/sgp4.对SGP4模型进行了改进,开发了SGP4-XP(SGP extended perturbations)预报方法.SGP4-XP相比现有SGP4模型的主要区别有:修改了月球摄动和大气密度模型、增加太阳光压摄动、将深空模型应用于全部空间物体等.SGP4-XP声称其精度更加接近SP(Special Perturbation)方法,同时计算时间消耗仅相当于之前SGP4模型的1.5–2倍,但具体实现以及可用的编目数据并未公布.

本文将对TLE编目深空物体的SGP4模型预报方法进行分析,给出SGP4模型实现中日月轨道计算时存在的位置偏差,并给出相应的改进方式,最后采用算例对比分析方式讨论日月轨道计算改进对预报精度的效果.

2 SGP4模型日月轨道计算分析与改进

SGP4模 型 分 为SGP4/SDP4两 部 分,其 中SDP4相对于SGP4增加了第三体摄动中的日月影响和特定轨道田谐项共振修正(深空模型),以提高深空物体(平周期大于225 min)预报精度.实际中SGP4/SDP4模型的使用已融合成统一的计算流程,仅以空间物体的平周期来决定是否加入深空模型计算.因此,本文中不再区分二者,合称SGP4模型.Hoots等[20]总结了美国SSN中所采用编目模型的历史发展,并详细给出SGP4模型的计算过程.而Vallado等[21]整理并维护了SGP4模型的源代码,十分接近于美国SSN编目过程中所采用的SGP4模型.本文对SGP4模型的分析对比即以此二者为具体参考标准.

2.1 SGP4模型的解形式

关于SGP4模型的理论分析,文献[22–25]已给出完整的描述.简单来说,TLE编目是平根数形式的一阶摄动分析解,其解的形式可表示为[25]

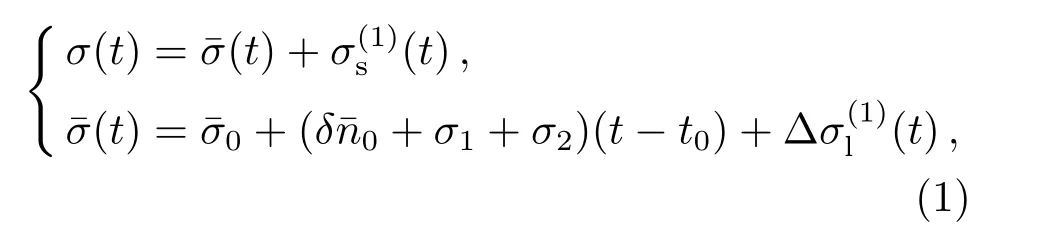
其中,t为预报时刻,t0为历元时刻,可以看作以平根数形式给出TLE编目,为不含短周期项的平根数,σ(t)即为预报结果,0为无摄运动项,σ1为一阶长期项,σ2为二阶长期项,(t)为一阶长周期项,(t)为一阶短周期项.

SGP4模型的具体实现仅包含了主要带谐项J2、J3、J4和大气阻力的摄动影响,另外对深空物体则增加了第三体摄动中的日月影响以及对特定轨道的田谐项共振问题修正.具体来说,SGP4深空模型增加了σ2与两个附加项的计算过程.

2.2 SGP4模型日月轨道计算分析

SGP4深空模型的第三体摄动项计算过程,仅考虑日月的平运动,即以日月在编目历元时刻瞬时根数的无摄运动来近似其真实运行规律.为了更加贴近实际日月轨道的长期变化,SGP4模型[21]以(2)–(3)式的形式给出某时刻的日月瞬时根数,即为所采用日月轨道计算的具体形式.

其中,下标S、L分别代表日、月,平运动速率n、偏心率e、轨道倾角i、升交点经度Ω、近地点幅角ω、平近点角M为地心平黄道下的轨道根数,(2)–(3)式中t1900.0是自1900年1月1日起算的儒略日.可以看出,SGP4深空模型[21]将太阳轨道近似为固定椭圆,仅有平运动的影响;对月球轨道的近似,仅考虑了升交点赤经ΩL,平近点角经度l(mean longitude),近地点经度γ(longitude of periapsis)随时间的变化.这样的近似在构造解析解时可以避免复杂的计算,但也会引入日月轨道计算造成的误差.

SGP4深空模型中日月运动近似引入的误差,可以分为初始偏差,即编目历元时刻的日月位置误差;外推误差,即以平运动近似日月真实运行时的位置误差.将(2)、(3)式的计算结果,与JPL(Jet Propulsion Laboratory)提供的DE432数值精密星历进行对比,转换到J2000地心平赤道坐标下,得到日月在不同时刻的位置偏差与平运动偏差,如图1所示,其中δn为平运动偏差.

从图1可以看出:SGP4模型对太阳轨道的计算以2021年1月至2023年1月之间为例,对太阳位置存在约2°的初始偏差,对平运动的估计比精确值大约0.1′·d-1,且存在周期性;对月球轨道的计算,以2021年8月至2021年10月之间为例,对月球位置存在约1°的初始偏差,对平运动的估计比精确值小约20′·d-1,且存在周期性.以外推10 d估计,SGP4模型日月轨道计算对日月估计存在约为2°–3°的位置偏差,且会随着外推时长不断增大.

图1 续Fig.1 Continued

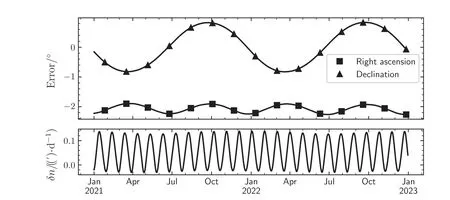
图1 SDP4日月轨道与JPL DE432星历相比的位置和平运动偏差,上:太阳(2021年1月1日—2023年1月1日),下:月球(2021年8月1日—2021年10月1日).Fig.1 Position and mean motion difference between SDP4 solar/lunar orbit and JPL DE432 ephemeris,top panel:solar(Jan 1st 2021—Jan 1st 2023),bottom panel:lunar(Aug 1st 2021—Oct 1st 2021).

2.3 改进方法

在不影响SGP4模型[21]第三体摄动求解过程的情况下,对日月轨道计算改进仍需要编目历元时刻的日月瞬根.由SGP4模型日月轨道计算过程可知,编目历元时刻的日月初始位置及其外推近似,直接决定了二者的位置精度.以卫星轨道预报数值方法为参考,对日月位置的精确计算,一般采用精密星历的方式来获取,如JPL DE系列.考虑到SGP4模型本身精度不是很高,同时为了减少日月位置计算对轨道预报效率的影响,可以采用一些较低精度的方法.

对太阳初始位置的计算,本文选取文献[26]中给出的计算方法,其精度约为0.01°,如下所示:

其中,轨道根数均为地心平黄道下的根数,aS为轨道半长轴,T为自J2000.0起算的儒略世纪数,表达式为

tJD为儒略日,ϵA为平黄赤交角.SGP4模型[21]中采用了固定值ϵA=23.4441°,(4)式同时给出ϵA随时间的变化,可以避免引入额外的坐标转换误差.外推计算时,对太阳运动仍然近似为无摄运动,采用SGP4模型[21]中太阳平运动值nS=0.9856°·d-1.

与太阳相比,月球的运行规律更加复杂,较为准确的月球位置计算通常以级数形式给出[26–27].本文选取SOFA(Standards of Fundamental Astronomy)3http://www.iausofa.org.提供的moon98子程序计算月球初始位置,其精度约为3′′,限于计算过程涉及级数项较多,略去具体公式形式.需要说明的是,moon98计算结果给出的是GCRS(Geocentric Celestial Reference System)坐标系下的位置矢量、速度矢量,需要进行坐标转换,并计算SGP4模型中所需要的平黄经根数.外推计算时,由于月球平运动nL变化较快,不再采用平运动近似方式,本文采用moon98子程序直接计算月球的升交距角uLt和升交点ΩLt,来近似月球的真近点角fL随时间的变化,如下所示:

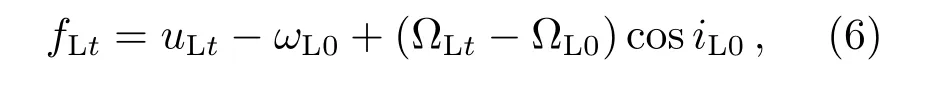
其中,下标为0的变量是编目历元时刻的日月轨道根数,下标为t的变量取外推时刻的日月轨道根数.

图2给出SGP4深空模型日月轨道与JPL DE 432星历相比的位置偏差,和采用改进方法之后的位置偏差,起算时间2021年9月1日,外推时间30 d.从图中可以看出,采用改进方法之后,太阳位置误差约外推30 d,约为1′–2′;月球位置误差,外推10 d约为5′,外推30 d约15′–20′.

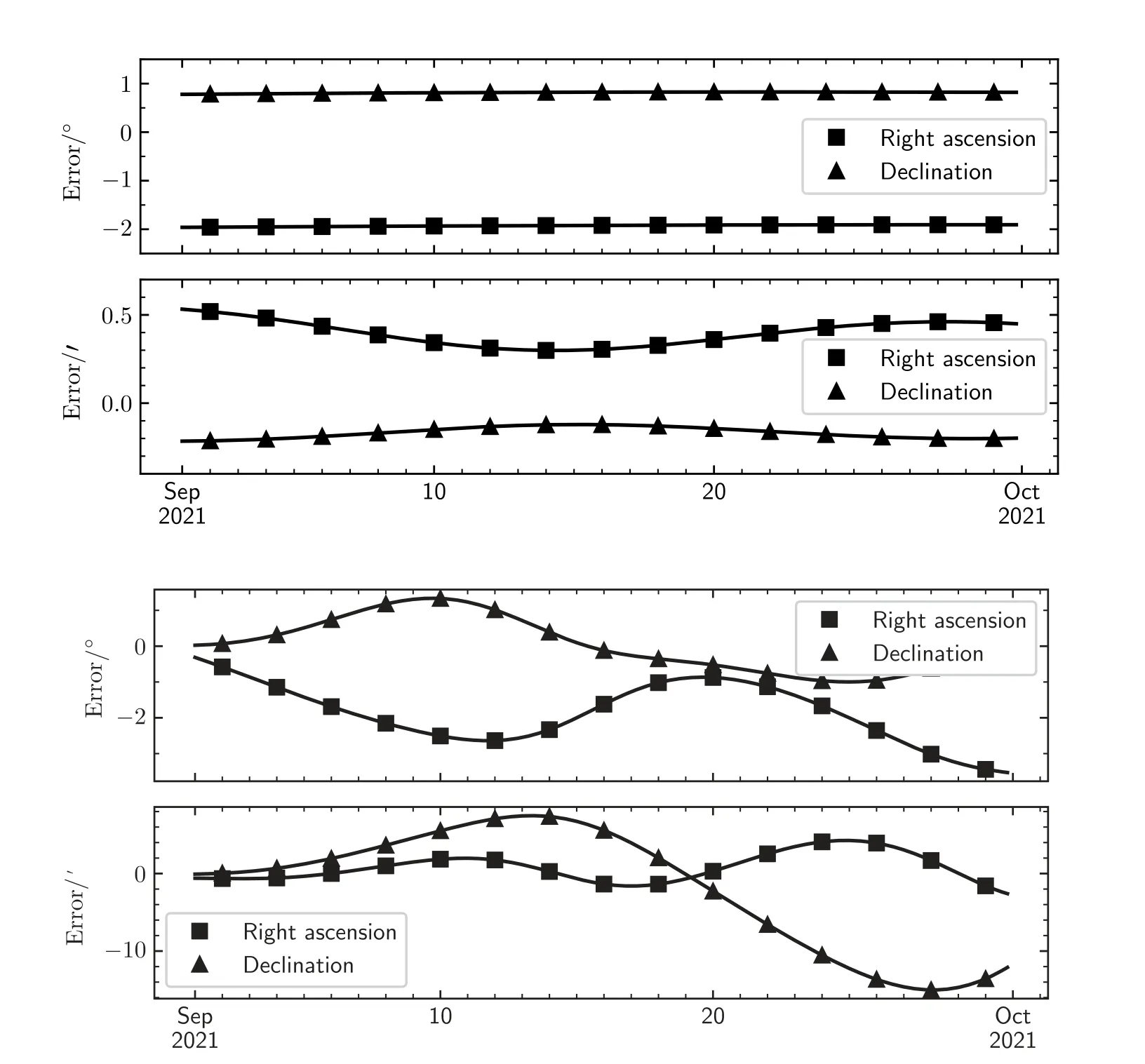
图2 外推时SDP4日月轨道与JPL DE432相比的位置偏差,与改进之后的位置偏差.上:太阳(2021年9月1日—2021年10月1日),下:月球(2021年9月1日—2021年10月1日).Fig.2 Position difference in solar/lunar orbit propagation—SDP4 vs.JPL DE432 and“corrected”vs.JPL DE432.Top:solar(Sep 1st 2021—Oct 1st 2021),Bottom:lunar(Sep 1st 2021—Oct 1st 2021).

准确地说,(4)式和SOFA moon98方法中,T要求采用TDB(Barycentric Dynamical Time)时间系统.而TLE编目中实际提供的是编目历元时刻UTC(Universal Coordinated Time)时间,参考文献[21]的计算过程,本文同样忽略了时间系统之间的转换,将UTC作为所有计算中的统一时间系统.此外,与TLE编目相适配的坐标系系统定义应该选取为TEME(True Equator Mean Equinox)[28],SGP4深空模型[21]仅将日月轨道变换到地心平赤道坐标系(Mean of Date),二者之间还存在由章动和赤经章动分量所联系的坐标系转换.由于地球章动量级约为10′′,限于当前改进方法的精度,这是可以忽略的.

3 算例分析

本文将改进后的日月轨道近似方法应用于文献[21]中SGP4模型第三体摄动计算,以算例形式来分析其对TLE编目深空物体预报精度的影响.理想情况下,对比算例应采用相同的观测数据、定轨策略,分别以原SGP4模型[21]和改进后SGP4模型为预报方法,进行轨道确定生成两组TLE编目,二者预报结果与参考精密轨道对比,是验证日月轨道计算改进可提高TLE编目深空物体预报精度的直接手段.若以真实编目中TLE数据为研究对象时,存在无法获取相应真实观测数据及定轨策略的问题.而采用伪“观测数据”时,定轨结果则同时受观测数据、定轨策略和计算改进等因素共同作用,无法单独体现计算改进对原TLE编目预报精度的影响.本文采用生成“近似”编目,使其与原始TLE编目的预报误差特性具有相似性,来选取轨道确定输入数据,可以近似“分离”观测数据、定轨策略与SGP4模型改进对定轨结果的影响.

本文算例选取激光测距卫星精密预报星历CPF(Consolidated Prediction Format)数据为参考轨道.激光测距卫星通常具有厘米级的测量精度,通过定轨可得到精密参考轨道来评估其他观测设备的数据精度[29].激光测距卫星还可获得CPF数据,这是由ILRS(International Laser Ranging Service)多个数据中心公开发布的轨道预报,包含了完整的力学模型,是卫星激光测距数据的定轨结果,具有约10 m量级的位置精度.以历史CPF数据作为“参考”轨道评估SGP4模型预报精度是足够的.算例分析步骤如下:

1.选取某深空物体TLE编目,进行轨道预报并与CPF数据参考轨道进行对比,给出其预报误差特性估计;

2.以CPF数据作为输入,以原SGP4模型为预报方法,在编目历元时刻重新进行轨道确定[30],通过调整CPF数据时间分布,生成与第1步原TLE编目误差变化趋势相近的“近似”编目,此时所选取的作为定轨输入CPF数据称为“近似定轨约束”;

3.将第2步中的“近似定轨约束”以日月轨道计算改进后的SGP4模型为预报方法,再次在编目历元时刻进行轨道确定,得到“改进”编目;

4.将原始编目、“近似”编目与“改进”编目进行预报,以最末次“近似定轨约束”数据时刻为零点,与相应的CPF数据参考轨道进行对比,以分析日月轨道计算改进对TLE编目深空物体预报精度的影响.

由于“近似”编目与“改进”编目都是基于相同输入数据的定轨结果,二者预报结果之间的对比可以反映出改进日月轨道计算的作用.所选取“近似定轨约束”使得“近似”编目与原TLE编目具有相似的误差趋势,则可以反映“改进”编目相比原TLE编目预报精度的提高,从而估计TLE编目深空物体轨道预报受日月轨道计算改进的影响.

本文选取TLE编目中的Etalon 1卫星和Galileo 23卫星作为分析对象.Etalon 1是由前苏联在1989年发射的专用激光测距卫星,轨道高度约19120 km,周期约676 min;Galileo 23是欧空局在2018年发射的伽利略卫星导航定位系统组成之一,具有卫星激光测距功能,轨道高度约23220 km,周期约845 min.Etalon 1卫星和Galileo 23卫星属SGP4模型中约定的深空物体,均不涉及共振问题计算,可更直接地反映出日月轨道计算变化对轨道预报的影响.选取2021年9月TLE编目数据,其历元时刻、平转动圈数m数及阻力项B*等如表1–2所示,其中Etalon 1卫星见表1,Galileo 23卫星见表2.

表1 算例中Etalon 1卫星TLE编目的平根数Table 1 Mean elements of Etalon 1 satellite TLE catalogues in test cases

表2 算例中Galileo 23卫星TLE编目的平根数Table 2 Mean elements of Galileo 23 satellite TLE catalogues in test cases

激光测距卫星CPF数据中位置、速度矢量的坐标系定义为ITRS(International Terrestrial Reference System),作为数据输入时,需要转换到SGP4模型相适配的TEME坐标系下.本文中仅选用CPF数据位置矢量作为定轨数据输入,数据点间隔300 s,采用全弧段模式.原TLE编目中B*项为0,定轨时保持B*原值为已知参数.定轨时对所有数据输入采用等权处理,采用最小二乘方法,以位置偏差和最小为约束条件来求解.“近似定轨约束”起止范围需要不断调整,以“近似”编目和原TLE编目预报误差的相似性来决定.本文算例所选用“近似定轨约束”要保证轨道确定所得“近似”编目(图3、图4中“OD without correction”)与TLE编目(图3、图4中“Original TLE”)的预报误差具有相对一致的变化趋势,即可认为“近似定轨约束”在最小二乘求解过程的约束作用与观测数据相同,是对观测数据的一个合理近似.本文在“近似定轨约束”的调整过程中发现,如果限制“近似定轨约束”时间范围在编目历元时刻之前,不能保证总是找到最佳的“近似编目”,最终取消时间范围限定,以满足获取最佳“近似”编目的要求.如图3和图4中所示,以“*”符号标出本文算例所选择CPF数据的时间范围.

图3中给出了Etalon 1卫星在所选3个时刻的TLE编目、“近似”编目和“改进”编目的预报精度对比,其中“近似”编目和“改进”编目采用了相同“近似定轨约束”.可以看出,“改进”编目结合改进后SGP4模型,在预报零点时刻之前对“近似定轨约束”的拟合精度优于TLE编目、“近似”编目表现;在预报零点时刻之后,位置误差约为1–2 km之间,变化规律较为一致.作为对比,原TLE编目、“近似”编目在预报零点之后,存在位置误差明显增大现象,变化趋势相对较为复杂,最大位置误差可达到2–5 km量级.

图3 Etalon 1卫星预报精度的对比—原始TLE,“改进”前/后定轨所得TLEFig.3 Comparison of propagation accuracy of Etalon 1—original TLE vs.TLEs from OD with/without corrections

同样的,图4中给出了Galileo 23卫星在所选3个时刻的TLE编目、“近似”编目和“改进”编目的预报精度对比.可以看出,在预报零点时刻之前,“改进”编目相比TLE编目、“近似”编目,对“近似定轨约束”的拟合精度仍优于后二者表现;在预报零点时刻之后,位置误差约为5–10 km之间,变化规律较为一致.对比原TLE编目、“近似”编目,在预报零点时刻之后,同样存在预报位置误差异常变化,变化趋势较为复杂的现象,其位置误差最大可达到约15 km量级.

图4 Galileo 23卫星预报精度对比—原始TLE,“改进”前/后定轨所得TLEFig.4 Comparison of propagation accuracy of Galileo 23—original TLE vs.TLEs from OD with/without corrections

上述算例分析表明,本文给出的日月轨道计算改进应用于SGP4模型是有效的,在使用相同观测数据进行定轨时,是可以提高TLE编目深空物体轨道预报精度的.

4 结论

TLE编目是空间碎片环境研究领域常用的一种数据,文献[21]给出与美国SSN生成TLE编目时最为接近的SGP4模型实现,是TLE编目轨道预报方法的“标准”参考.本文分析SGP4模型第三体摄动计算过程发现,其日月轨道计算存在初始位置偏差和平运动近似偏差;其对日月位置的估计,在外推10 d时约为2°–3°误差,且随外推时长不断增大.日月轨道计算偏差会直接影响SGP4模型第三体摄动项,引起二阶长期项σ2与一阶长周期项(t)变化,导致深空物体轨道预报位置误差增大.通过选择更加准确的日月轨道计算方法,并对月球运动以直接计算真近点角方式来近似,可改进SGP模型中日月轨道计算,使得其外推10 d时,将太阳位置偏差减小到1′量级,月球位置偏差减小到10′量级.选用CPF数据作为参考轨道,本文以生成“近似”编目和“改进”编目的方式,对Etalon 1和Galileo 23卫星进行重定轨,来验证日月轨道计算改进是可以提高相应TLE编目预报精度的.对于深空物体TLE编目,以Etalon 1和Galileo 23卫星为例,其轨道预报位置误差存在异常增大现象,且变化趋势相对复杂.采用改进日月轨道计算后SGP模型所得“改进”编目,在预报时刻零点之前,其拟合精度优于TLE编目和“近似”编目表现;在预报零点时刻之后,“改进”编目预报位置误差变化规律也较为一致,且增长小于相应TLE编目.本文对TLE编目深空物体的误差特性研究有一定帮助,日月轨道计算偏差会引起其位置误差趋势异常变化,混淆SGP4模型本身的误差演化特性;以“二次”轨道确定来提高TLE编目预报精度时,对于深空物体应考虑SGP4模型日月轨道计算改进,可以获得更好的定轨结果.