基于MATLAB/GUI的一级倒立摆控制仿真软件设计*

袁新娣，陈 睿

(赣南师范大学 物理与电子信息学院，江西 赣州 341000)

1 引言

倒立摆是一种典型的复杂控制系统，具有非线性、多变量、强耦合和自然不稳定的特点[1].许多工业工程和军事工程中的运动控制系统，其控制思想和方法均来自于倒立摆的控制机理，例如，工业机器人行走的平衡控制、海洋钻井系统的稳定控制，火箭发生器的垂直控制等等[2]，所以倒立摆的控制一直是一个经典的控制实例，在控制原理课程中，经常以倒立摆为控制对象对控制算法进行学习.但是倒立摆控制系统体积大、体重也大，不适合将设备搬到课堂进行讲解演示，学生学习或者设计控制算法时如果每次都要到实验室测试，也将带来很多的不方便.为了方便师生的教与学，有较多的文献对倒立摆系统进行仿真分析与设计，文献[3]设计实现线性二级倒立摆基于MATLAB/GUI仿真，但文献对仿真方法描述笼统，仿真结果也不清晰，GUI界面设计不够直观等不足；文献[4]对环形倒立摆系统应用三维建模软件进行建模，然后应用MATLAB/SIMULINK进行仿真分析，文献[5]中对单级倒立摆根据物理原理建模，然后基于建立的模型应用MATLAB/SIMULINK进行仿真控制分析，大部分介绍倒立摆仿真控制的文献都是使用MATLAB/SIMULINK工具进行，MATLAB/SIMULINK工具的使用需要对该MATLAB熟练掌握，其直观性不够，对初学控制原理知识的同学，掌握该工具比较困难.所以，本文首先根据一级小车倒立摆的物理原理建立数学模型，然后应用MATLAB软件的GUI工具设计一个方便直观的倒立摆仿真控制软件，通过该软件可以修改倒立摆系统参数，选择控制算法，观察运行效果等功能，对学习控制原理带来了较好的帮助.

2 倒立摆数学模型

为了对倒立摆进行控制仿真，首先必须建立倒立摆的数学模型，本文以如图1所示的小车倒立摆为例进行分析，长度为2l、质量为m的摆竿通过铰链安装在质量为M的小车上面，小车由直流电机驱动，如果不给小车驱动力，倒立摆将向左或向右倒下，即系统不稳定.如果在水平方向给小车施加控制力u,控制小车在水平方向移动，那么倒立摆将保持在垂直位置上不倒下[6].

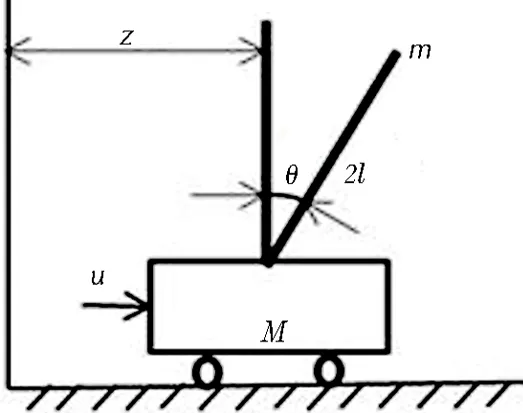
图1 一阶小车倒立摆示意图

设小车瞬时位置为z，摆杆偏角度为θ，则摆心瞬时位置为(z+lsinθ)，当忽略摆杆与电机惯性、各类摩擦力及风力的情况下，根据牛顿第二定律得式(1).

(1)

由于绕摆轴旋转运动的惯性力矩与重力矩平衡，所以式(2)成立.

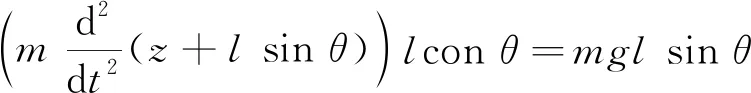
(2)

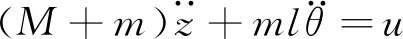
(3)

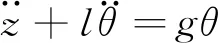
(4)

联立式(3)式(4)解得式(5).

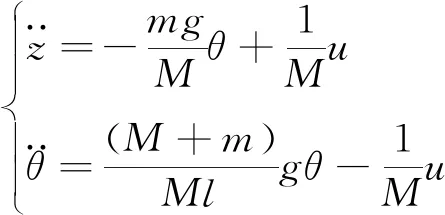
(5)

(6)

其中

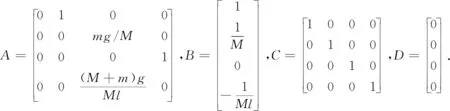
式中g是重力加速度，取值9.81.为了分析系统的能控性与能观性，假设系统的M=1kg,m=0.5kg,l=0.3m,计算能控性判断矩阵[B,AB,A2B,A3B]的秩等于4，能观测性判断矩阵[C,CA,CA2,CA3]T的秩等于4，所以系统具有完全能观性和完全能控制性.

3 倒立摆控制GUI仿真软件设计框架

使用MATLAB的GUI控件工具相，建立如图2所示的仿真软件前面板界面，界面上包含倒立摆运行时的摆杆的角度变化及小车位移变化随时间变化的坐标，倒立摆参数设置，倒立摆的二维动画，控制方式选择，算法参数设置等模块.用户可以在界面右下角任意设置小车倒立摆的参数，然后在控制方式模块的下拉菜单中选择控制算法，右下角设置完成算法中的参数，点击“确定”按钮时系统将读取用户输入的信息，进行仿真，并把仿真的结果显示在界面左边的坐标轴上，同时右上角显示小车移动的二维动画效果图.本软件设计了倒立摆常用的3种控制算法：极点配置算法，线性二次型最优控制算法，PID控制算法.

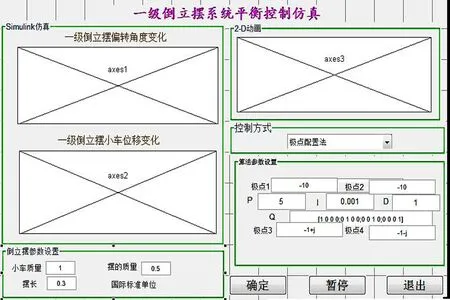
图2 GUI仿真软件前面板

3.1 倒立摆极点配置控制算法仿真设计

极点配置控制算法的基本原理是：当被控系统满足完全能控条件时，将系统的状态信息反馈到系统的输入端，使得闭环系统的极点成为用户要求的极点.由前面倒立摆数学模型分析可知，一级倒立摆系统完全能控，所以可以通过调节反馈参数达到极点任意配置的目的.本软件应用全状态反馈方法进行极点配置，即从系统的4个状态处设置增益为[k1,k2,k3,k4]的负反馈(以公式(5)为系统状态空间描述，系统的输出就是系统的状态)，系统的希望极点从图2所示仿真平台右下角输入， GUI回调函数中计算负反馈增益[k1,k2,k3,k4]的指令为：

Qc=ctrb(A,B);

j1= str2double(get(handles.edit15, 'String'));% 从前面板读取极点1

j2= str2double(get(handles.edit16, 'String'));% 从前面板读取极点2

j3= str2double(get(handles.edit17, 'String'));% 从前面板读取极点3

j4= str2double(get(handles.edit18, 'String'));% 从前面板读取极点4

EA=diag([j1,j2,j3,j4]);

PP=polyvalm(poly(EA),A);

Ks=[0 0 0 1]*inv(Qc)*PP; %计算反馈矩阵增益

[t,x,y]=sim('ploeandlqr.mdl') %通过调用siumlink文件形成输出信号.

sim()函数调用的程序ploeandlqr.mdl如图3所示.点击平台的“确认”按钮后，平台运行如图4所示，

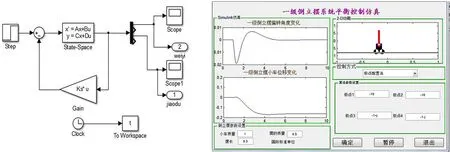
图3 ploeandlqr.mdl程序 图4 选择极点配置算法后运行的界面

可见在阶跃信号作用下，当极点配置为-10、-10、-1+j、-1-j时，杆的偏移角在5秒后恢复到零，稳定后小车位移为-0.16 m.

3.2 倒立摆的线性二次型最优控制设计

线性二次型最优控制，就是设计最优控制率u*(t)，使得式(7)表示的性能指标J最小.

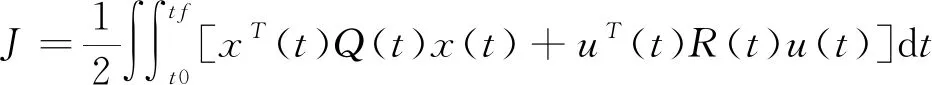
(7)

式中Q(t) 是n*n维正定(或者半正定)对称矩阵，R(t)是r*r对称矩阵，x(t)是系统状态，u(t)是系统输入.同时，最优控制规律是一个状态线性反馈规律，控制向量u*(t)由状态向量x(t)反馈生成，并且呈线性关系.在MATLAB中利用LQR指令可以方便的获取系统线性二次型最优控制的状态反馈系数.本软件从GUI前面板界面输入参数Q(t)和R(t)，回调函数使用如下指令获取线性二次型最优控制的反馈系数：

R= str2double(get(handles.edit28, 'String'));%获取R(t)

Q= str2num(get(handles.edit30, 'String'));%获取Q(t)

Ks=lqr(A,B,Q,R); %计算反馈矩阵增益

[t,x,y]=sim('ploeandlqr.mdl'); %通过sim函数调用仿真程序

Sim()调用的程序ploeandlqr.mdl如图3所示，GUI运行的结果如图5所示，可见在阶跃信号作用下，当R(t)=0.5，Q(t)=[100 0 0 0 ; 0 1 0 0 ; 0 0 100 0; 0 0 0 1]时，摆杆的偏移角在4 s后恢复到零，稳定后小车位移为-0.07 m.当改变Q与R的值时系统的输出将发生变化.

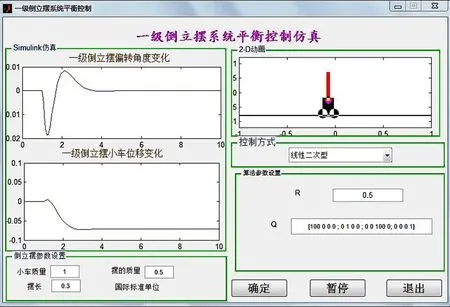
图5 选择线性二次型最优控制算法后运行的界面

3.3 倒立摆的PID控制设计

PID(Proportion Integration Differentiation)控制规律如式(8)所示，

(8)

式中m(t)是控制器的输出，e(t)是控制器的输入.算法主要通过调整比例环节系数Kp，积分环节系数KI及微分环节系数KD三个参数，使得被控制系统达到预定的性能指标.

PID控制器可以作用于系统的前向通道，也可以作用于系统的反馈通道，本软件将PID用于反馈通道，并且结合期望极点配置的反馈系数控制倒立摆的性能指标.回调函数实现PID控制的指令主要为：

p=[-10,-7,-1.901,-1.9];%设置极点

Kpid=place(A,B,p); %反馈系数

KP=str2double(get(handles.edit19, 'String'));%获取KP

KI=str2double(get(handles.edit20, 'String'));% 获取KI

KD=str2double(get(handles.edit21, 'String'));% 获取KD

[t,x,y]=sim('pidkz.mdl'); %调用simulink仿真程序

Sim()函数调用的程序pidkz.mdl如图6所示，软件运行结构如图7所示，可见在阶跃信号作用下，当KP=18，KI=0.001，KD=1时，摆杆的偏移角在4 s后恢复到零，稳定后小车位移为-0.017 m.

图6 pidkz.mdl程序 图7 选择PID控制算法后运行的界面

4 总结

本文首先分析了倒立摆系统的数学模型，确定其具有完全能观性与完全能控性，然后通过Matlab 的GUI工具箱建立软件的前面板，GUI文件通过调用回调函数实现了前面板输入相关参数，后台执行程序，然后又将执行结果显示在前面板的效果.设计的GUI仿真软件为控制原理的学习带来了形象、直观的效果，提高了学生的学习兴趣.另一方面，本设计可以在现有设计框架下进行拓展，增加倒立摆的其他控制算法，比如滑模控制、神经网络控制、模糊控制等，为学习更多的算法提供便利.