基于遗传优化DHNN的噪声图像识别研究*
2022-12-12乐江源李梦超郑景林
郭 勇,乐江源,李梦超,郑景林
(赣南师范大学 物理与电子信息学院,江西 赣州 341000)
离散型Hopfield神经网络属于非线性动力学系统,它的稳定性可用“能量函数”描述.在满足条件时, DHNN的“能量”在网络运行过程中不断减少,最后趋于稳定值.给图像添加噪声,运行该神经网络后,网络状态将不断更新,图像最终能被成功识别.目前,已有DHNN应用于雷达多目标跟踪[1]、电网故障诊断[2]、电动车挡泥板成型[3]、图像加密[4]、手写数字识别[5]等研究中.
基于Hebb规则的外积法是基于样本为两两正交的[6],通常由外积法设计的DHNN权值矩阵是对称矩阵,可以证明对称阵对任意初始状态的DHNN网络都可达到稳定的平衡点[7].杨守建等[8]采用Hopfield神经网络对加噪条件下的道路交通标志进行识别,当噪声密度大于60%或旋转角度大于±15°,复杂度越高的图像识别率下降越快.史兴宇等[9]将DHNN运用于边缘或中部遮挡以及施加15 dB以内的高斯白噪声的车牌二值图像中识别车牌数字,能正确识别.朱丽萍等[10]使用线性函数替换符号函数sgn(x)的方法使DHNN对噪声在25%以内的数字图像还原率提高了5%-11%,然而还原后的图像有提升空间.综上所述,由于传统方法设计的DHNN在“能量”达到极小值时,系统则处于稳定状态,属于局部收敛,因此对于噪声图像识别能力有限,当噪声水平增强时,识别效果不理想.
遗传算法(GA)是基于Darwin进化论和Mendel遗传学说,采用随机搜索优化技术,能够寻求全局最优解[11].目前有学者将DHNN与遗传算法结合优化样本空间,提高求解效率[12].有学者基于DHNN采用改进的遗传算法以优化具有不同数量电子元件(如晶体管)的超大规模集成电路的结构[13].可见,已有将遗传算法与DHNN相结合的优化应用.
本文拟引入遗传算法,增强DHNN对噪声图像的识别能力.通过MATLAB编程对含有不同噪声水平的图像进行识别,以3个交通标志噪声图像为例,验证遗传算法在增强DHNN的噪声图像识别能力上有效性,并研究遗传算法应用于DHNN识别噪声图像的特点.
1 DHNN权值矩阵
DHNN是一种单层的、输入/输出为二值的反馈网络.
DHNN拓扑结构如图1所示.

图1 DHNN拓扑结构
图1中,x1,x2,…,xn及y1,y2,…,yn是网络的状态量,x表示输入,y表示输出.第1层为输入层,第2层为输出层,第0层的状态量直接来自第2层.激活函数为符号函数sgn(ui),在MATLAB中为hardlims函数.DHNN输出的计算公式如式1-2所示.

(1)
yi(t+1)=sgn(ui(t+1))
(2)
DHNN每一时刻的状态对应一个能量,表达式如式(3)所示.
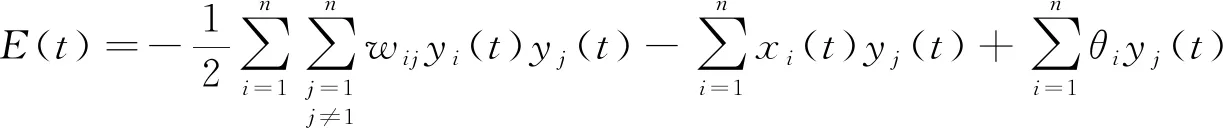
(3)
DHNN是否处于平衡状态由“能量函数”是否达到极小值决定.如果在系统状态变化过程中,“能量函数”的能量值不断衰减,最后达到极小值,则DHNN是稳定的.每一个能量值都对应一权值矩阵和阈值,当能量达到极小值时,使系统稳定的权值矩阵和阈值便被确定.通常,权值矩阵可以通过外积法预先设计.
设有m个n维记忆模式,要设计网络连接权wij和阈值θ,使这m个模式正好是网络能量函数的m个极小值.设
uk=[u1,u2,…,un]T,k=1,2,…,m
(4)
其中,m表示的是模式的类别数,n为每一类模式的维数,uk是模式k的向量表达.
要求网络记忆的m个模式矢量两两正交,因此各神经元的阈值和网络连接权矩阵按式(5)计算

(5)
则所有矢量uk在1≤k≤m时都是稳定点.
按照上式计算的权值矩阵为对称阵,可以使“能量函数”获得极小值.然而对称权值矩阵仅仅是局部最优解,并非全局最优解.在图像识别中,当图像受噪声干扰时,权值矩阵为对称阵的DHNN对图像的还原能力有限.设计了左转弯、右转弯和直行3种交通标志,首先将其二值化为30×30的二进制格式;然后运用MATLAB创建DHNN(此时为对称权值矩阵),为图像添加不同水平的随机噪声(0.1、0.2、0.3),考查图像还原能力,不同噪声下外积法设计的DHNN识别图像结果如图2所示.

图2 不同噪声下外积法设计的DHNN识别图像结果
由图2可以看出,外积法设计的DHNN对图像进行识别,噪声水平在0.1、0.2时识别识别效果可行,当随机噪声水平达到0.3时,图像识别效果较差.欲增强DHNN对噪声图像的识别能力,须优化网络参数,遗传算法是一种能够优化网络参数使“能量函数”具有最小值的方法.当然,采用遗传算法优化后的网络依然稳定.
2 遗传算法优化权值矩阵
2.1 算法原理
遗传算法是一种枚举式搜索方法,通过模拟自然界的进化机制寻求目标函数的最优值[14].在DHNN中,设有m个输入,n个输出,则权值矩阵为m×n,阈值矩阵为n×1,因此变量共有(m×n+n)个.当权值矩阵与阈值有最优解时,式(3)具有最小值.在遗传算法中,种群中的每个个体有一个染色体,每个染色体恰好包含了一个DHNN的所有权值和阈值信息,因而每个染色体含有(m×n+n)个基因.
随机创建初始种群,个体数量为N,种群中每个个体的基因均用一串具有相同的编码方式的二进制代码表示,采用标准二进制代码编码.因此初始种群表示为N×(m×n+n)的矩阵,矩阵的每一列代表一个基因.通过对种群中每个个体染色体上的基因进行选择、交叉、变异等仿生物学操作,产生下一代并计算其适应度值,适应度高的个体有更高的可能性继续繁衍,适应度低的将被淘汰,多次进化后适应度最高个体基因即为该DHNN的权值和阈值的最优解.
定义i为遗传算法的代数,第i代种群的每个个体适应度值计算方法如下:将第i代种群的每个个体的所有基因信息输入到DHNN,先求第i代网络每个输出与第i-1代网络对应的每个输出之差的绝对值,再求和.个体适应度值越小,适应度越高,适应能力越强.特别地,第0代种群(即初始种群)每个个体适应度值是将第0代种群每个个体的基因信息输入DHNN,计算当前网络的所有输出,先取绝对值再求和.
2.2 算法流程
首先确定遗传算法的参数(种群个数与维数、最大繁衍代数,种群编码的二进制位数等),根据参数对种群进行二进制编码,创建初始种群;
接着令i=0,按照下列步骤完成DHNN权值和阈值寻优的过程,遗传算法优化DHNN参数的流程图如图3所示.

图3 遗传算法优化DHNN参数的流程图
3 设计实例
3.1 实例验证
针对像素为30×30的原始二值图像,设计DHNN为30个输入神经元,30个输出神经元,创建初始种群(父代)数量为1 000,种群的每个个体含有930个基因,每个基因按照20位二进制进行标准化二进制编码,因而初始种群为1 000×930的随机矩阵.
采用遗传算法按照图3流程对权值矩阵和阈值不断进化,繁衍50代,得到最优权值和阈值.为3种交通标志二值图像添加相同水平的噪声(0.3),考查图像还原能力,遗传算法优化DHNN后图像识别结果如图4所示.由图4可以看出,当随机噪声水平达到0.3时,图像识别效果比采用外积法更好.

图4 遗传算法优化DHNN后图像识别结果
3.2 遗传算法效果分析
3.2.1 还原能力分析
当图像的输入噪声水平增加时,分别考察外积法设计网络参数与遗传算法优化网络参数后DHNN对图像的还原能力.以30×30的左转弯二值图像为考察对象,输入噪声水平从0.05增大到0.95,间距为0.05,设计遗传算法中种群数量为500,繁衍200代,采用二进制位数为20的标准二进制编码方式编码,获得网络输出.以原始图像为参考,计算输出图像的PSNR(峰值信噪比),用以反映DHNN对噪声图像的还原能力.输出图像的PSNR与输入噪声水平的关系如图5所示.
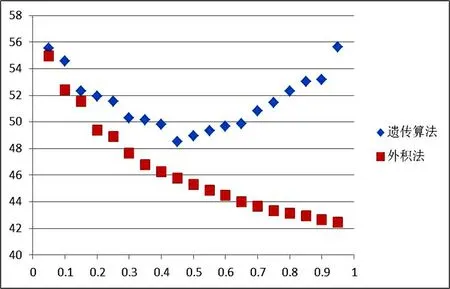
图5 输出图像的PSNR与输入噪声水平关系
由图5可知,采用遗传算法繁衍一定的代数后,DHNN的还原能力在相同水平的输入噪声下比采用外积法的更好;随着图像的输入噪声水平增加,采用外积法设计的DHNN还原能力逐渐降低,而采用遗传算法其还原能力先减小后增大,且在噪声水平为0.5时最低.由于图像为二值图像,当输入噪声水平大于0.5,尤其是大于0.7时,其噪声图像几乎与原图像反相,人眼已能识别.由此可知,遗传算法优化参数后,DHNN能够识别与原二值图像近乎反相的噪声图像.
3.2.2 收敛速度分析
虽然遗传算法优化权值矩阵与阈值增强了DHNN识别噪声图像能力,但是为了实现全局收敛,即在任意初始种群经过有限次进化都能达到最优解,算法收敛速度慢.以图4(c)为例,像素为30×30的图像,目标函数(即个体适应度值)趋于稳定值的迭代次数约为500次,当迭代次数大于200时,目标函数收敛速度非常慢,最优解对应的目标函数值随迭代次数变化图如图6所示.

图6 最优解对应的目标函数值随迭代次数变化图
遗传算法按照自然界“优胜劣汰”的进化原则对参数进行优化,根据图3可知,初始种群的大小、选择操作、交叉和变异的概率均会影响收敛速度.由图6可知,若能降低初始种群的目标函数值,迭代次数将减少.有研究先通过DHNN迭代计算降低能量,再在局部范围内采用遗传算法对权值进行优化,提高了算法的收敛速度[15].此外,在个体进化过程中,不让优质的个体参与交叉和变异,使之直接成为子代,能加快寻优的进程,这也是算法改进的方向.
4 总结
本文分析了DHNN的能量函数与系统稳定性的关系,讨论采用外积法设计的DHNN对噪声图像的识别能力有限的问题,引入遗传算法对网络参数进行优化.通过对3种交通标志图像添加不同水平的噪声,分别考察外积法与遗传算法优化网络参数后DHNN对噪声图像的识别能力.结果表明,采用遗传算法优化后,噪声图像识别能力得到增强.此外,分析了采用遗传算法优化的DHNN对噪声图像还原能力及算法的收敛速度,并针对收敛速度慢的问题提出了改进方案.
