基于Himawari-8卫星数据的青藏高原大气可降水量反演算法研究
2022-12-12江金昊刘海磊王乙竹张升兰
江金昊 刘海磊 王乙竹 张升兰
(成都信息工程大学电子工程学院,四川 成都 610225)
0 引言
大气中的水汽及其变化是天气和气候变化的主要驱动力,是影响气候变化和维持地球生态平衡的关键要素[1],其在降水和灾害性天气预报、大气辐射研究、水循环和全球气候变化研究等方面具有重要应用[2-3]。此外,大气中的水汽含量也是影响遥感应用的主要物理量之一,如地表参数精确反演、遥感数据大气订正等均需要精确的水汽信息[4-6]。
大气可降水量(precipitable water vapor,PWV)是表征大气水汽的一个重要参数,指单位面积空气柱里含有的水汽总量[7]。目前,有多种技术手段可以进行PWV的探测,根据探测手段可分为无线电探空、地基遥感和卫星遥感[8-10]3类。虽然无线电探空、地基遥感探测精度较好,但这两类探测方式仅能给出固定点上空的水汽分布情况,通常无法准确、客观地反映某一地区水平尺度上的水汽含量梯度变化[11-12]。
青藏高原占中国领土面积的四分之一,平均海拔高度4000 m以上,是世界上海拔最高、地形最复杂的高原[13]。青藏高原地气作用过程,尤其是能量与水分循环过程对亚洲季风、东亚大气环流及全球气候变化均有重要影响[14]。因此,高原的水汽分布、来源、输送等一直都是非常关注的高原气象科学问题[14-15]。
极轨气象卫星每天仅可以提供同一地区一至两次的PWV观测,加之青藏高原云量偏多使极轨卫星获取的有效数据非常有限[16]。相比之下,静止气象卫星具有观测区域大、频次高的优势,是目前获取青藏高原高时空分辨率水汽信息的有效手段[17]。因此开展基于静止气象卫星的青藏高原高精度水汽探测研究具有重要实际应用价值与现实意义。
目前,静止气象卫星没有近红外和微波水汽探测通道,因此其PWV反演算法主要是基于热红外通道数据展开的。PWV红外反演算法大致可分为线性分裂窗算法、分裂窗方差协方差比值算法和物理分裂窗算法[18-19],这些算法均是基于水汽在分裂窗区通道吸收差异原理开发的[9]。线性分裂窗算法和分裂窗方差协方差比值算法通常假定分裂窗区通道发射率相同,且邻近像元需存在一定的温度差异,这一定程度限制了算法的精度和适用性。物理分裂窗算法由于考虑了辐射传输过程,其精度优于线性分裂窗算法[20]。
传统的分裂窗算法实质是利用水汽在分裂窗区通道吸收差异原理开展的。在干燥环境下(比如PWV<2.0 cm),水汽吸收差异引起的分裂窗区通道亮温差较小(可小于1.0 K),这可与通道发射率不确定性引起的亮温差、仪器噪声和定标误差相当。算法更容易受到发射率不确定性和观测误差的影响,因此低水汽环境下仅利用分裂窗通道估算PWV存在较大的不确定性[19]。青藏高原平均海拔高度超过4000 m,水汽含量相比同纬度地区明显偏低,再加之高原地形复杂、发射率等辅助数据缺乏,使仅基于分裂窗区通道无法获取青藏高原可靠的PWV信息[9]。
近年来国际上都在发展新一代静止气象卫星,比如日本的Himawari-8/9、美国的GOES-R、中国的 FY-4A/4B和欧洲的MTG-I/S等陆续发射升空[21-22]。新一代卫星搭载的成像辐射仪在时间、空间、光谱分辨率及观测精度等方面显著提升,可提供更加丰富的大气温度、湿度信息,这为青藏高原高海拔、低水汽环境下的高精度PWV反演提供了良好的机遇。
目前,AGRI/FY-4A和ABI/GOES-R已发布了总水汽含量和分层水汽产品。AGRI和ABI的水汽产品算法相似,都是基于一维变分(1DVAR)方法,利用卫星的多通道观测进行物理迭代,实现大气温度和湿度廓线的反演[7,23]。之后,对反演的大气廓线进行积分获得分层和总水汽含量。由于静止气象卫星成像仪通道较少,这给大气温度和湿度廓线的反演带来较大不确定性。此外,该方法对大气廓线初始场的依赖性较强。已有的研究表明AGRI和ABI产品在低水汽情况下的误差较大,其中AGRI水汽产品在青藏高原的相对误差可达30%~80%[7]。
Himawari-8搭载的高级成像仪(advanced himawari imagers,AHI)除提供2个红外分裂窗通道以外,还具备6.2 μm、7.0 μm和7.3 μm附近的水汽通道观测能力[24-25]。这有助于中高层水汽探测,也有利于提高低水汽环境下的PWV反演精度。目前,Himawari-8卫星并未发布官方PWV产品,使用AHI数据开展青藏高原PWV反演的研究较少。本研究将利用AHI多通道红外观测和其他辅助数据,基于神经网络技术构建一种适用于青藏高原低水汽情况下的PWV反演算法。
1 数据和方法
1.1 数据
1.1.1 Himawari-8数据
Himawari-8是日本气象厅的新一代静止气象卫星,于2014年10月7日发射,2015年7月7日正式业务化运行,位于140.7°E的赤道上空,覆盖范围为60°N~60°S,80°E~160°W。其搭载的成像仪AHI共有16个光谱通道,包括3个可见光通道,3个近红外通道和10个红外通道[22]。每10 min可进行一次全圆盘扫描,每2.5 min对日本周边地区进行一次区域扫描。目前,Himawari-8卫星没有发布PWV业务化产品。
AHI具有2 个红外分裂窗通道和6.2 μm、7.0 μm和7.3 μm 3个水汽通道观测能力。利用中光谱分辨率大气辐射传输模式(MODTRAN5.2)开展这些通道的水汽敏感性分析,图1给出了不同高度中纬度冬季标准大气湿度廓线5%变化,所引起的通道亮温变化情况。AHI的6.2 μm、7.0 μm和7.3 μm通道权重函数的峰值在400 hPa、520 hPa和580 hPa附近,通常情况主要提供中上层水汽信息,受地表参数(如地表温度和发射率)的影响较小。11.2 μm和12.3 μm窗区通道主要对低层水汽更为敏感,权重函数峰值为800 hPa和780 hPa附近。
通道敏感性在不同大气条件下会有所不同,青藏高原平均海拔高度达4000 m,AHI水汽吸收通道具备提供整个空气柱水汽含量的潜力。此外,红外分裂窗区通道的差分吸收也能提供PWV。因此,选用AHI的水汽吸收和分裂窗区5个红外通道亮温进行水汽反演。表1为使用通道的主要特征,使用数据的时间是2016年1月1日-12月30日。此外,还使用了AHI L2级云检测产品,主要用于分辨晴空和云天像元。AHI数据下载于日本宇宙航空研究开发机构地球观测研究中心(http://www.eorc.jaxa.jp/ptree/index.html)。由于JAXA的P-Tree数据网发布的云检测产品只有白天的数据,因此本研究仅使用了0-12 UTC的数据,时间间隔为1 h。
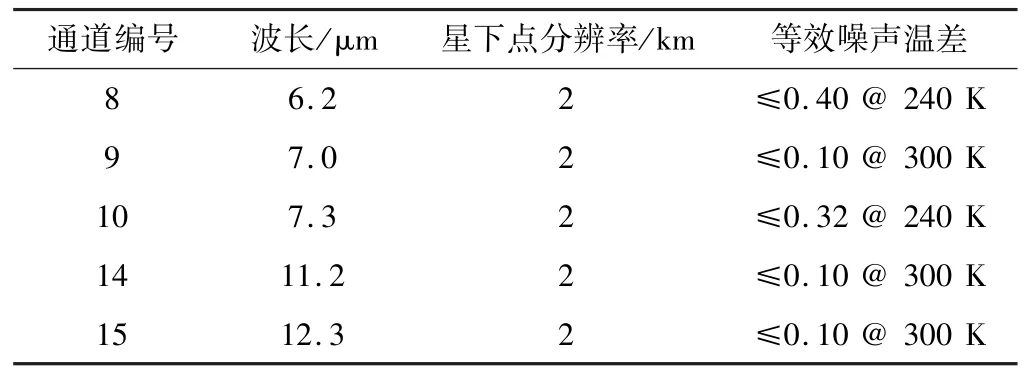
表1 算法所使用AHI通道的主要特征
1.1.2 GPS PWV数据
全球定位系统(global positioning system,GPS)地基站点在接收信号时的大气延迟可用于大气水汽反演,精度通常为1~2 mm[11]。GPS PWV数据已被广泛应用于卫星水汽产品的评估和验证。选用2016年1月1日-12月30日的逐小时GPS PWV作为真实参考数据,用于建模和验证AHI反演的PWV精度。
青藏高原24°N~40°N,80°E~105°E共 32个GPS站点(图2),站点海拔高度从2585~4705 m,年均PWV变化3.03~10.05 mm。2016年的逐小时PWV变化0.2~35.0 mm。
1.1.3 GFS PWV预报场
全球天气预报系统(GFS)可以提供全球范围0.25°,0.5°和1°的网格PWV数据。预测时间步长分别为0~240(间隔为3 h),240~384(间隔为12 h)。模式预报每天在UTC 00、06、12和18时运行。根据已有的研究,数值预报可以有效提高基于卫星数据的大气参数估算精度[26]。将0.25°分辨率的GFS PWV数据作为模型的一个输入,以期待通过融合卫星观测和GFS PWV的预报信息,并减少云污染对卫星反演结果可能的影响,进而提高PWV反演精度。
美国大学大气科学研究联盟(UCAR)提供了非常便捷获得GFS历史数据子集的方式(https://rda.ucar.edu/datasets/ds084.1/)。实时的GFS PWV预报数据可从NOAA NCEP下载(https://www.nco.ncep.noaa.gov/pmb/products/gfs/)。由于GFS仅提供3 h间隔的数据,根据AHI的观测时间和经纬度信息对GFS PWV进行了时空插值。
1.2 神经网络模型
神经网络是由多个神经元构成的非线性模型,其可以较好地描述训练数据的输入和输出变量的非线性和复杂关系,也被广泛应用于地球物理参数的反演和估算[26-27]。本研究选用多层前馈神经网络来构建青藏高原PWV快速反演模型。
模型的输入主要包括AHI的5个红外亮温、卫星观测角、GFS PWV预报场、海拔高度、经度、纬度、儒略日和小时。利用最近邻方法提取与GPS站点时空匹配的AHI像元多通道亮温,对GFS数据进行时空插值以匹配AHI观测。经过时空匹配和云检测处理,最终形成21156组样本。为分析GFS PWV预报场对反演模型的影响,将建立2个模型,模型1是基于全部预测因子的NN模型;模型2则为未包含GFS PWV的NN模型。针对2个模型均随机选择一半数据作为训练数据,余下的数据作为验证数据集。
1.3 误差分析
为验证方法的可靠性和评价结果的质量,使用相关系数(R)、均方根误差(RMSE)和偏差(Bias)3个统计指标:
其中,PWVNN和PWVGPS分别是神经网络模型反演和GPS站点的和分别是神经网络模型反演和GPS站点的PWV平均值,N是数据样本总数。
2 结果与讨论
2.1 误差分析
图3给出了模型1和2反演结果与GPS PWV的二维直方分布图。两模型反演值与GPS PWV数据的相关系数大于0.94,RMSE小于1.52 mm,这意味两个模型均能有效反演PWV。模型1的PWV数据比模型2更集中于1∶1线,这说明模型1估算值与GPS PWV吻合度更高。模型 1的 R、RMSE和 Bias分别为0.957、1.33 mm和-0.004 mm,模型2则分别为0.943、1.52 mm和0.01 mm。模型1和2输入数据的差异是有无GFS PWV,这意味着引入GFS PWV预报场数据可以提高PWV反演精度。
图4为两个模型PWV反演误差(反演值-GPS PWV)直方分布图,两模型误差均呈现正态分布,绝大部分误差在±4.0 mm以内(>97.3%样本)。模型1和2的PWV反演误差小于2.0 mm的数据点分别占90.75%和87.51%,误差小于1.0 mm的数据点则分别为72.1%和67.1%。Lee等[27]利用AHI多通道亮温、经纬度和观测角数据,基于机器学习模型估算了东北亚地区的PWV。模型加入了更多与水汽相关的影响因子(比如海拔高度、时间信息和PWV预报场),因此展现了与GPS PWV的更好的吻合度。
2.2 误差时空分布特征
通常情况下,卫星反演PWV的精度会受大气含水量、海拔高度、经纬度和地表类型等多种因素影响,进而呈现一定的时空分布特征。为进一步分析本文模型的精度,逐个站点评估了PWV反演的精度。图5给出了模型1和2的R和RMSE空间分布图。总体而言,两个模型在大部分站点均有较好的表现,RMSE主要在0.5~2.5 mm,相关系数主要在0.9~0.98。相比之下,由于引入了GFS PWV预报场,模型1在各站点均比模型2精度好,展现了较高的R和较小的RMSE。值得注意的是,也存在个别站点误差偏大,RMSE可达3.0 mm,这可能跟云污染或训练样本代表性有限有关。
此外,对模型误差的季节变化特征进行分析。图6给出了模型的月平均相关系数、均方根误差和偏差的时间序列。两个模型的月平均RMSE和R展现了相似的季节变化特征。模型RMSE均从1月1.0 mm开始上升,7月达到最大值3.0 mm,然后又逐渐下降。整体来说,夏季呈现出较大的RMSE,冬季RMSE较小。RMSE趋势跟PWV的季节变化特征相似,意味着水汽含量数值对RMSE有明显影响,这与之前的研究结果是一致的[7,23]。冬季模型的相关系数低于其他季节,这可能跟冬季PWV动态变化范围小有关。两模型的月平均偏差小于0.25 mm,说明没有明显的高估或者低估。
总体而言,神经网络模型反演结果与GPS PWV吻合度较好,具体表现在较高的相关系数、较低的均方根误差和平均偏差,说明该算法可以有效反演青藏高原PWV。
神经网络建模时使用了GPS站点数据。当有GPS PWV参考数据可用时,推荐使用模型1进行PWV的反演。没有GPS PWV可用时,构建模型1将变得非常困难。此时,可以使用模型2进行PWV反演。具体操作如下:(1)收集研究区域有代表性的地表、大气廓线数据(如月平均的同化模型数据);(2)利用辐射传输模型(如MODTRAN或者RTTOV)模拟卫星观测的多通道亮温;(3)基于模拟的多通道亮温、大气廓线积分的PWV以及模拟计算的输入各种辅助参数,构建PWV神经网络反演模型。模型2精度略差于模型1,其优点是在无GPS PWV数据可用时,可以通过模拟数据来构建模型。
3 结论
新一代静止气象卫星为高时空分辨率PWV探测提供了良好的机遇。利用Himawari-8 AHI多通道红外亮温、GFS PWV预报场和其他辅助数据,基于神经网络技术构建了适用于青藏高原低水汽环境下的PWV快速反演方法。引入水汽吸收通道和GFS PWV预报场,可以有效提高低水汽情况下的PWV反演精度。基于GPS PWV数据的验证结果表明,反演的PWV的R和RMSE分别为0.957和1.33 mm,这意味着模型能够提供青藏高原较高精度的PWV。此外,由于反演过程不需要辐射传输计算,因此算法速度远高于物理反演算法,适合于实时的PWV反演。
分析了模型误差的时空变化特征,大部分站点RMSE误差小于2.0 mm,说明算法表现较稳定可靠。模型RMSE和R展现了一定的季节变化特征,RMSE夏季误差大于冬季,与大气水汽含量变化展现了相似的变化趋势。冬季R小于其他季节,这可能跟冬季PWV动态范围小有关。仅利用青藏高原地区32个台站数据进行建模,没有进行基于无线电气象探空的PWV数据的验证、对比,在其他地区的适用于性有待于进一步验证。FY-4A/B的星载成像仪与AHI通道配置相近,算法也适用于FY-4A/B数据。
