基于DNA编码和二维混沌系统的图像加密算法
2022-12-12唐浩哲黄源源任震宇成江宇李朝荣
唐浩哲 黄源源 任震宇 成江宇 李朝荣
(1.成都信息工程大学网络空间安全学院,四川 成都 610225;2.宜宾学院人工智能与大数据学部,四川 宜宾 644000)
0 引言
近年来,随着移动网络时代不断地飞速发展,人们能够更便捷地获取信息。然而,在与其他人交流互动的过程中,个人信息容易泄漏这个安全问题变得层出不穷。研究人员也随之发现了网络信息安全问题,并认为解决网络信息安全以及传输中的问题刻不容缓。传统的加密方法,如DES(data encryption standard,数据加密标准)、AES(advanced encryption standard,高级加密标准)等都只能保证应用在数据量较小的环境时,能够有效保护多媒体版权,增强数据安全性[1]。
由于图像所承载的信息具有高冗余度、巨大的数据存储容量、较强的像素之间信息相关性等特点,所以使用图像信息加密技术需要使用更加快速有效的加密算法。由此,传统的图像加密编码方法(DES、AES等)已经无法满足当前的数字图像编码加密安全性需求。
该领域的研究者在对图像加密算法的实验和研究中遇到过如下一些问题。
首先,CIE L*a*b*颜色空间在图像处理和传输中都扮演了重要角色,被研究者应用到图像的实验和研究中。许莉等[2]提出了一种基于Lab颜色空间的运动目标检测方法。通过选择L*a*b*的颜色特征作为前景/背景进行分析的特征,分开处理亮度和色度,得到每个像素在各个通道上的不同信息;然后通过使用背景差和帧差相结合的查分监测模型对背景进行处理,最后通过背景差分得到运动图像目标;不同的颜色空间也被加以应用,金汉均等[3]提出一种在HSV颜色空间中结合小波变换做的图像检索应用研究方法,但由于方法没有融合图像的多特征进行检索,导致其准确度不高。
其次,通过应用DNA编码来处理图像,DNA编码是将计算机科学与分子生物学相结合而产生的一个新兴学科,通过模拟DNA生物操作,进行伪DNA计算来实现信息加密[4]。在实验过程中,遇见了以下的一些问题:Zhang等[5]提出了一种基于DNA编码和二维Logistic混沌映射的图像加密算法,但发现这种算法得到的图像难以抵挡已知明文的攻击;田海江等[6]提出一种图像加密算法通过基于普通混沌系统和DNA动态编码,结果因DNA的运算规则不够复杂,使得加密算法太过单一,图像安全性也不高;因为其加密算法的不可逆现象,Bonny B R等[7]提出了一种基于DNA编码的对称密钥加密算法,结果由于密钥长度不够,容易被暴力破解。
对于图像加密,有不少学者也尝试将混沌加密算法与人工智能领域中的DL(deep learning,深度学习)板块相结合,通过卷积神经网络的理论,使用足够多的数据集去训练加密算法或者超混沌系统,从而使算法处理后的加密图像具有很高的安全性和抗噪能力。陈炜等[8]提出一种利用深度学习来压缩重构图像,再使用复合混沌系统、滑动置乱与矢量分解组成的加密算法对图像进行加解密处理。但使用该算法加密的图像并没有得到很高的图像信息熵值,加密图像不具有足够高的随机性和安全性。
超混沌系统有很多特征:具有优秀的伪随机性、对初始状态及结构参数的极端敏感性以及其轨道具有不可预测特性等[9]。使用混沌序列成为随机密钥,能够达到一次一密的效果。这样的操作,在理论上是不可破的。然而,低维混沌序列存在许多问题,比如低维混沌序列会因计算机字节长度的限制,从而对混沌的动力学特性造成影响,使得加密算法不够成熟;而且低维混沌系统产生的混沌只可短期预测,这让其产生的混沌序列具有较差的随机性,且获得的密钥空间小,加密后的结果安全性能低[10],易于破译。相反,高维混沌系统能够通过对更多的参数进行控制变化,提高图像置乱的随机性,从而增强图像加密的安全性。因此,多维超混沌系统成为了一个很好的方法来确保混沌系统的复杂性。
为此,本文提出的基于DNA编码和二维混沌系统组的图像加密算法,结合了超混沌系统组(超混沌Chen系统、二维Logistic映射和广义Arnold映射)和DNA编码运算对目标加密图像进行分块加密。不仅能有效提高图像加密过程密钥的敏感性和传输过程中的安全性,还成功通过了包括差分攻击在内的攻击形式,以及灰度直方图、相关系数计算分析等,具有较高的安全性。
1 基础理论
1.1 CIE L*a*b*色彩空间
CIE L*a*b*是被常用来描述人眼可见的所有颜色的最完备的色彩模型[11]。即使目前绝大多数的彩色图像信息的输入和输出均是根据RGB三色空间作为标准的,但是由于RGB三色通道均包含了其亮度信息,导致彩色图像的三色间具有很强的相关性,从而影响图像在后面部分加密置乱时无法得到一个更随机安全性更高的的加密图像。
CIE L*a*b*色彩空间是基于1931年的CIE XYZ色彩空间的一种更复杂的色彩空间,后者是采用X、Y、Z3个刺激值组成。X表示创建的非负曲线的圆锥体响应,Y表示亮度,Z表示蓝色分量。由于RGB到CIE L*a*b*之间没有直接的转换公式,故需要先从RGB到CIE XYZ,再到CIE L*a*b*,以CIE XYZ作为颜色的中间层,起到起承转合的作用。这两个转换步骤具体为
1.1.1 RGB—>CIE XYZ
RGB和CIE L*a*b*色彩空间的转换公式:
可见,XYZ和RGB在互相换算时,参数之和刚好为1。例如:X=0.433953×R+0.376219×G+0.189828×B,其中0.433953+0.376219+0.189828=1,这样就做到了在转换前后能够获得同等范围的映射[12]。
1.1.2 CIE XYZ—>CIE L*a*b*
CIE(国际照明委员会)在1964年提出了CIE L*a*b*均匀颜色空间。从XYZ到L*a*b*的转换计算为
其中,Xn,Yn,Zn为CIE标准光源照射在完全漫反射体上后,再经过完全漫反射至观察者眼中的三刺激值。通常情况下,Xn,Yn,Zn为常数且值均为255。另外,L∈[0,100],a∈[-127,127],b∈[-127,127]。真彩Lena图像转换至CIE L*a*b*色彩空间后的结果如图1所示。
1.2 Chen混沌
2005年,通过状态反馈控制构建了Chen氏混沌系统,其方程为
其中,x,y,z和ω作为系统的状态变量,a,b,c,d和r为系统的控制参数。根据研究显示:当a=35、b=3、c=12、d=7且0.085≤r≤0.798时,系统将表现为超混沌运动。
1.3 Logistic混沌系统
1.3.1 一维Logistic映射
单从数学式分析,一维Logistic映射是一个相当简单的映射,但其实它在通信传输上拥有较高的复杂度。也有不少人在此基础上研究图像的加密问题,其数学公式为
Xn+1=Xn×μ×(1-Xn)
其中,μ作为Logistic参数,且μ∈[0,4],而研究表明,当变量X∈[0,1]时,此系统处于混沌状态。
然而,在现在的各类攻击手法作用下,普通的一维Logistic系统由于参数太少,无法生成复杂的混沌系统,无法使加密算法拥有较高的安全稳定性,因此本文将应用Logistic映射的二维混沌系统进行图像加密。
1.3.2 二维Logistic映射
为保证加密后的图像具有一定的安全性,引入一个新的二维Logistic函数。与现有的混沌映射相比,它具有更广泛的范围内混乱,更好的遍历性和混沌性。其数学公式为
其中,μ、λ1、λ2和γ均为控制参数,通常情况下,取μ=4。经过计算得知:当λ1=0.9、λ2=0.9、γ=0.1时,此时的二维Logistic系统处于混沌状态[13]。为了研究及其应用,提出一个置乱转换(CMT),以有效地改变图像的像素位置。结合二维Logistics与CMT,可以进一步实现图像加密算法。
1.4 猫脸变换(Arnold)系统
1.4.1 离散Arnold变换
猫脸变换最早是由俄国数学家Arnold引入的,其数学式如公式为
其中,xn和yn均为实数且xn,yn∈(0,1),取模运算mod将(xn,yn)的相空间限制在 [1,1]×[1,1]内。
与一维Logistic混沌系统相同,离散Arnold映射因参数太少无法生成复杂混沌系统,无法有效保证加密过程的安全性。因此在文中使用广义Arnold变换参与加密流程。
1.4.2 广义Arnold变换
当然,Arnold映射同Logistic映射一样,也是一种混沌映射[14]。其数学式为
其中,xn和yn是大小为N×N的图像置乱前所处的像素位置,xn+1和yn+1为置乱后所处的像素位置,p,q,N均为正整数且p、q的值小于N。由于二维Arnold映射数字化是具有周期性现象[15],所以基于Arnold映射的图像在加密时如果知道加密算法,通过在某一个密文空间以任意状态进行迭代,都能够在有限步骤中内被恢复为明文。例如:当p=40,q=8,N=124且iter=5(迭代轮数)时,此时加密图像可恢复原样,因而将Arnold映射和Logistic映射结合起来,能够达到更好的加密效果。
1.5 DNA编码规则和DNA基础算法
1.5.1 DNA编码规则
生物研究表明:DNA是由4种脱氧核苷酸通过碱基互补配对组成的双螺旋链式结构。4种脱氧核苷酸分别为腺嘌呤(A)、鸟嘌呤(G)、胸腺嘧啶(T)和胞嘧啶(C),碱基互补配对规则为A与T配对、G与C配对。根据电脑二进制中1和0互补的特性可以利用DNA的碱基互补原则,用两位二进制数值来表示4种脱氧核苷酸,且由于不同规则的核苷酸的二进制数值指定是不同的,所以满足碱基互补配对的规则组合有8种[16],如表1所示。由于图像在计算机中是由像素组成,且每个像素值都可以通过编制DNA单链来加密,然后通过互补单链来解密。以灰度值来举例:设一个像素的灰度值为8bit,其二进制表示为“11000101”,用表1的规则1来编码,可得编码为“TACC”。

表1 DNA编码规则
1.5.2 DNA基础运算
整个加密过程中可能使用到的DNA编码运算方法分为DNA的加法、DNA的减法和DNA的异或。DNA的加法、减法和异或运算类似于传统的代数运算[17],运算规则如表2~4所示。

表2 DNA加法

表3 DNA减法

表4 DNA异或
2 加密过程与加密算法
本次加密算法使用真彩图像进行实验,先利用RGB转CIE L*a*b*色彩空间原理将原图转换至该色彩空间,然后在Matlab中使用函数使其变为灰度图像,再做进一步操作。加密过程如图2所示。
文中对图像加密分为4部分:
步骤1 根据RGB图像至CIE L*a*b*色彩空间的原理和两步转换规则,转换输入的RGB图像I0的色彩空间,并将图像降至二维,分别得到CIE L*a*b*色彩空间下的图像I1和降维后图像I2。
步骤2 根据超混沌Chen系统生成4个混沌(8bit)序列,应用于后续DNA编码置换的过程。
步骤3 根据二维Logistic混沌映射规则,对I2图像进行扩散置乱,得到图像E1,再根据广义Arnold混沌映射规则,对E1图像进行操作得到图像E2。
步骤4 利用步骤2获得的X',Y,Z,H4个混沌序列,结合DNA编码规则将图像的每个像素点进行对应转换,对图像E2进行置乱操作,得到最终加密图像E3。详细加密流程图如图3所示。
加密流程具体步骤如下:
输入真彩图像I0,参数初值
输出加密图像E3
步骤1 将真彩图像I0进行色彩空间的转换,得到CIE L*a*b*色彩空间的图像I1。
步骤2 将步骤1得到的图像I1通过降维函数将其改变为灰度图像I,并将图像矩阵I转换成大小为M×N的二维矩阵I2。
步骤3 将图像I2分解为4个相等大小子块,编号依次为Ti(i∈[1,4]),并将图像的行列数都补成可以被4整除的数。由于4块的加密方法均相同,加密方法中混沌序列加密过程仅根据其中1块进行说明,另外3块加密方式类似。
步骤4 根据Chen系统所需的4个初值参数,采用ody45的方法和微分方程进行求解,输入超混沌Chen系统的初始值x,y,z,ω,生成4个混沌(8bit)序列X',Y,Z,H,将应用于后续DNA编码置换的过程。
步骤5 初始化Logistic映射控制参数:μ=4,λ1=0.9、λ2=0.9、γ=0.1,根据二维 Logistic公式进行迭代映射,得到图像序列I3和加密图像E1。
步骤6 广义 Arnold变换矩阵的形式为A=[1,p;q,1+p·q];按照输入的密钥p,q构建广义Arnold变换矩阵A,将输入的图像E1在A的作用下进行迭代置乱加密得到密文图像E2,并得到图像序列I4。
步骤7 根据步骤4获得的X',Y,Z,H,取其前8MN项,并不重复地对T1,T2,T3,T4依次将连续8个比特数进行比特合并,得到4个长度为MN的随机序列,分别记为K1,K2,K3,K4。接着,令Q=K1⊕K2⊕K3⊕K4。对于I4中的第i(i=1,2,…,MN)个像素点,构建公式:
可以得出,A、B、C、D∈(1,2,3,…,8),又根据DNA序列编码和其运算规则,按照规则A,将密文图像E2中的T1部分图像块进行DNA编码,按照规则B,将T2部分图像块进行编码,按规则C,将T3部分图像块进行编码,按规则D,将T4部分图像块进行编码;然后对对应的图像块根据编码规则进行DNA运算操作;将运算结果再进行上一步骤的运算,成为扩散过程。最后将分别加密的图像块按照原始的分块方式进行拼接,合并成完整的最终加密图像E3。
解密为加密的逆向流程。在文中不做详细说明。
3 仿真测试
3.1 测试环境
本次使用Windows10,内存16G,CPU为Inter i5的电脑配置进行实验,测试平台为Matlab 2018a。作为对比,选用Lena图(256×256像素)进行测试。该算法的仿真测试从密钥空间、灰度直方图、相关系数、差分攻击、信息熵等5个方面来进行,从而得出本文算法是否具有足够高的安全性。图4为本文算法测试的真彩Lena明文图像和加密后的密文图像。图5为本文加密图像的解密结果。无法简单用肉眼分辨解密后图像和加密前原图的差异,基本判定该算法能够将图像信息进行加密传递,并让接收者也能够顺利解密获得该图像信息。
3.2 密钥空间分析
如果要让加密的效果达到最好,也就是能够接受多种密钥的攻击,需要足够大的密钥空间。研究数据显示:当整个算法的密钥空间达到2100时才能够说加密图像的安全性达到了可以保障的程度[18]。本次使用了64位的CPU,假设计算机浮点数的计算精度可以达到10-14,则整个加密算法的密钥空间可以达到(1014)5=1070。经过计算,所要求的2100≈1.27×1030,1070远大于2100,故满足要求。因此,可以得出初步结论:这种加密方式有足够大的密钥空间,能够有效地抵御绝大部分的物理攻击。
3.3 灰度直方图分析
灰度直方图是将数字图像中的所有像素,按照灰度值的大小,统计其出现的频率。灰度直方图是灰度级的函数,表示图像中具有某种灰度级的像素的个数,反映图像中某种灰度出现的频率[19]。一个理想的加密算法应该使任何灰度图像在加密之后得到的密文图像中尽可能少地呈现出明显的特征,即灰度直方图在加密后呈现均匀分布。密文直方图的分布越均匀,说明该加密算法就越安全[20]。图6是该算法应用到Lena图前后灰度直方图的对比,可以看出:加密之后的灰度直方图分布均匀,说明加密后的图像不具有任何对解密有用的明显信息,证明加密系统有效且安全性高。
3.4 相关系数分析
一般情况下,一张未加密的、完整的图像相邻像素之间的相关性较高,可以达到90%及以上。为防止攻击者对图像进行统计分析,需要降低图片相邻像素的相关性。本次实验随机选取原始图像和加密图像上5000对相邻像素点(水平、垂直、对角方向),并计算像素间的相关性。
其中:x,y分别代表图像中相邻像素的横、纵方向灰度值;cov(x,y)代表协方差;D(x)和E(x)分别代表方差和平均值。表5给出了原始图像和加密后图像在水平方向、垂直方向、对角方向相邻像素的相关性。并与文献[21-22]比较,以表现本文算法的安全性之高。

表5 相关系数测试结果
由表5可知,当明文图像的相关系数均非常接近于1,同时加密图像的相关系数均非常接近于0时,就表明明文图像的相邻像素点之间具有较强的相关性,而加密图像的相邻像素点之间基本不具备相关性[23]。图7和图8分别为Lena灰度图加密前后的相邻像素点在水平方向、垂直方向和对角方向的相关性散点相图。
3.5 差分攻击分析
本文的加密算法,使用的密钥和明文图像相关,使得明文图像对密文图像非常敏感,故只要稍微修改一点明文图像的像素值就会使密文图像大相径庭,从而保证加密算法的安全性。这里,假设明文图像为I,则H,W分别为明文图像的长与宽,C1为加密图像,通过将I中某一个像素值进行微调(将像素值加1bit或减1bit),得到调整后的加密图像C2。引入两个相关概念,分别是像素改变率(number of pixels change rate,NPCR)和归一化平均变化强度(unified average changing,UACI)。
其中,C1(i,j)和C2(i,j)分别代表明文图像像素值被微调之前后所对应的密文像素值。NPCR的值越接近100%,或UACI的值越接近33%,此时的加密算法处理后的加密图像敏感性越高,抵抗差分攻击的能力越强。表6是本文算法与文献[8,21,25]的算法比较,可以看出,本文算法处理图像能够有效抵御差分攻击。
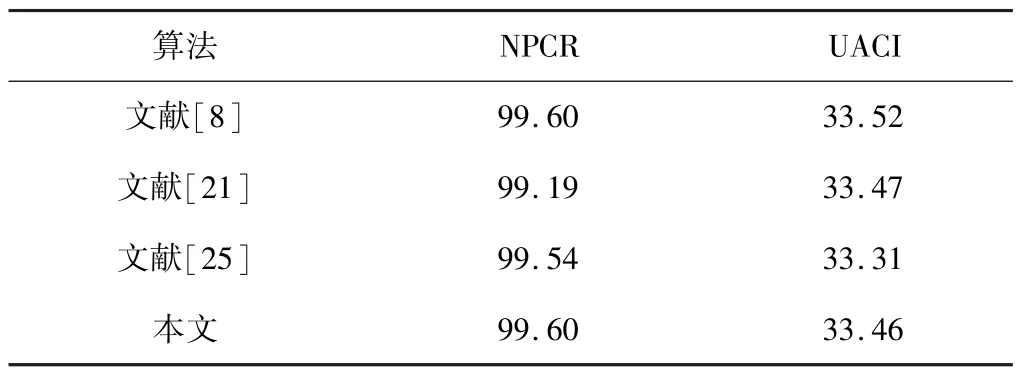
表6 NPCR/UACI测试结果 单位:%
3.6 信息熵
1948年,香农提出了“信息熵”的概念,为解决信息量化的问题。信息熵被定义为描述系统的不确定性的程度,可以用来表示图像信息的不确定性。计算公式如下:
其中,p(mi)表示某信息mi出现的概率。根据实验数据知,信息熵越大,越接近完全随机的图像信息熵8,则该加密图像的灰度值分布越均匀、随机性越大、信息传递越安全。表7为本文算法和文献[8,25,27]的算法加密图像后的信息熵测试结果。

表7 加密图像信息熵
与其他算法比较,可以看出本文算法得到一个较大的信息熵值,非常接近理想值。这表明该加密图像发生信息泄露的可能性极小,也间接证明了加密算法的安全性。
4 结束语
提出了一种将DNA编码规则和超混沌系统相结合的图像加密算法。通过转化图像色彩空间、降低图像维度;利用Chen超混沌系统、二维Logistic系统、广义Arnold系统和DNA编码序列的多重运算来达到安全高效加密明文图像,实现图像置乱和像素值扩散过程。先转换图像颜色空间,再分别通过Chen超混沌系统、二维Logistic映射和广义Arnold映射组成的超混沌系统对图像像素值进行扩散、置乱操作,最后结合DNA编码规则对处理后的图像再次置乱加密,得到最终的密文图像。本文经过密文图像密钥空间、灰度直方图、相关系数、差分攻击和信息熵值等测试方法,从多方面专业化地验证了该算法处理后的加密图像的安全性。下一步将研究深度学习和基于DNA序列卷积神经网络的图像加密算法。计划针对深度学习中的LSTM神经网络,通过预测时间序列,生成预测新混沌信号,并使用Pytorch等工具进行混沌序列的训练,得到新混沌信号,再结合多维混沌系统和DNA编码,能够更进一步提升图像加密的安全性。
致谢:感谢大学生创新创业训练计划项目(202010621260)对本文的资助。
