超临界机组快速模型预测控制算法及应用

汪红旭，郭骁，石尧，谢磊*

(1.黄冈大别山发电有限责任公司，麻城 438304；2.浙江大学，杭州 310027)

0 引言

从工程热力学角度看待，超临界状态指将水的临界状态点参数定义为22.115Mpa和374.15℃，即一旦水的状态达到或者超出该参数，则不会存在饱和水和饱和蒸汽间的汽水共存二相区。在火力发电过程中使用超临界机组，其主蒸汽压力一般为24Mpa，可以避免汽包的使用，发电效率一般为41%，高于常规亚临界机组对应的38%发电效率[1]。因此，随着科学技术的不断进步与电力工业的不断发展，可以确定日后在新增大规模火电机组中使用发电效果更佳的超临界机组将会成为必然的选择。

对于大规模超临界火力发电机组来说，系统的协调控制至关重要，对于单元机组的良好协调控制可以保障机组安全、稳定运行[2]。然而，超临界机组是一个多输入多输出的复杂对象，其非线性特征明显，且具备相对较大的惯性与延迟，因此，使用传统控制手段实现超临界火电机组控制极为困难，需要开发实施可以应用的先进控制策略来满足系统控制的要求。

模型预测控制技术（MPC），作为近几十年来极具代表性的先进控制算法[3]，主要由三大基本模块构成，即预测模型、反馈校正以及滚动优化。MPC相较于传统比例积分最为显著的特点在于其可以处理约束，而且其在应对多输入多输出系统的控制效果更佳[4]。MPC在每个控制周期预测未来动作，并计算最优的操作变量增量，从而实现未来行为的优化。经过几十年的发展，MPC已经获得了大量工程行业的认可，包括能源[5]、航空航天工程[6]、和汽车工业[7]等领域。由于MPC的良好控制效果以及超临界机组的自身特性，MPC可以在超临界机组中使用以实现对于超临界机组的协调控制。

超临界机组对于MPC算法的应用同样提出了部分要求，为了保障机组运行，在应用MPC算法的过程中，火电机组对控制的时效性极为关注，需要确保在系统的采样间隔内，快速地计算获得满足约束的MPC解，从而避免安全事故的发生。为了提高MPC的在线计算速度，国内外已经有众多学者进行了相关研究，且根据其远离主要可以分为两大类：其一是对 MPC 算法进行适当改进从而简化在线计算，其中最具代表性的方法名为显示控制算法。显示控制算法由Bemporad[8]在2002年提出，主要分为离线计算与在线优化两个部分。在线运行前首先需要进行离线的操作，对状态空间进行适当划分，随后依次对每个子空间设计线性控制律，因此，在线计算时即可以直接调用各个子空间的控制率，从而避免在线计算。然而，一个较为明显的缺点是，状态分区的大小与控制律的计算会随系统控制问题规模的增大随之呈现指数增长，这会对存储量提出极大挑战。第二类算法则是开发更为高效的优化问题求解策略从而提高在线求解速度，目前主要为有效集算法[9]、内点法[10]以及他们的衍生算法如：不可行有效集法[11]，对偶有效集法[12]、惩罚函数内点算法[13]等等。

本文为超临界机组提出了一种快速模型预测控制算法，从而实现对超临界机组这个多输入多输出系统的良好控制。首先通过对超临界机组的机理分析，并获得了单元机组的机理模型。随后通过推导获得了机组在工作点处的线性模型，以便于MPC的实施。考虑到形成的MPC优化问题黑塞矩阵的不变性，离线进行SVD分解以提取特征信息，便于从无约束最优解中选取满足约束的次优解。最后，通过使用MATLAB，对超临界机组中应用快速MPC算法进行仿真以检验控制效果，并通过其与MATLAB内置的内点法计算函数进行比较以检测所提算法的快速性与合理性。

1 超临界机组控制模型

1.1 非线性机理模型建立

通常情况下，超临界直流锅炉的制粉系统采用直吹式方案：首先在磨煤机中将煤磨制成煤粉，研磨好的煤粉通过一次风机产生的风被吹送到炉膛中进行燃烧。从整个机组的动态特性而言，直吹式制粉系统主要影响其延迟与惯性，下面将分别对二者进行公式描述。

直吹式制粉系统纯延迟环节主要体现给煤机中煤的传送时间与管道中煤粉在一次风作用下的输送时间，则通过将这些纯延迟环节相加，可以得到：

其中，r'm代表实际煤量，rm表示给煤机煤量，τ为传送延迟时间，通常情况下，延迟时间通常为15s到35s左右。

此外，给定进入锅炉的煤粉量r0与磨内存煤量M时，制粉系统惯性环节的平衡公式可以用下式表示

该惯性环节主要体现磨煤机细粉分离器中的分离过程。

煤粉量可以根据磨煤机特性获得：

其中，磨的出力系数用符号kb表示，煤的可磨性的修正系数为符号fh，fw代指煤的水分修正系数，fr则表示煤粉的细度修正系数。

为了构建汽水分离器的动态模型，我们通过对其压力关系进行分析。首先，使用如下的公式：

用以描述水冷壁的传热过程。其中，Qi为炉膛烟气与水的交换热量，Q0为炉膛烟气与金属的交换热量，Cm表示金属的蓄热系数。

在给定t1管壁平均温度与t0金属管平均温度，金属与水的换热系数λ1，考虑如下的换热模型：

则将其带入可以得到

对于过热区模型，在本文中，为了简化起见，假定吸入热量等同于增加气体的体积流量。对于理想气体，给定气体比热c，m为气体的质量。其吸热量dQ有：

过热区中差压与流量的关系为：

将体积流量与热量的关系代入上式并进行积分可以得到差压与流量及热量的关系：

使用一个拟合系数n可以将上式近似简化为：

n通常取1.3～1.5，根据不同机组的运行数据其取值也会随之改变。

对于汽轮机，其将热能转化为机械能，随之将机械能转移到发电机中，并通过发电机切割磁力线产生电能。相对于锅炉的化学燃料燃烧过程，汽轮机中能量转化非常迅速，因此其动态过程很快。

考虑如下汽轮机的进气量方程

其中，μt代表汽轮机调门开度，机前压力pt，ts为过热蒸汽温度。此外，机组输出功率与调节压力之间关系为：

其中NE表示输出功率，p1为调节压力。

1.2 工作点线性化模型

上一节已经通过机理分析得到了超临界机组非线性模型，工程上，往往采用通过在非线性模型工作点进行线性化的方法获得超临界机组的线性控制模型。根据所搭建的机理方程，确定模型输入为燃料指令μB与汽轮机调门开度μT，模型输出为机组功率输出NE与机前压力pT。推导获得超临界机组传递函数模型如下：

其中：

2 模型预测控制基础

给定x(k)∈Rnx和u(k)∈Rnu，分别为k时刻的系统的状态和输入变量，则可以假定系统由如下所示的线性模型系统表示：

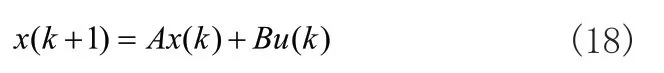
在得到模型后，可以使用模型预测控制方法对系统进行良好控制。为了实施MPC，首先需要确定其目标函数。本文假定预测时域和控制时域相同，均为NP，则模型预测控制的目标函数选取如下：

其中Q和R为正定对角矩阵：

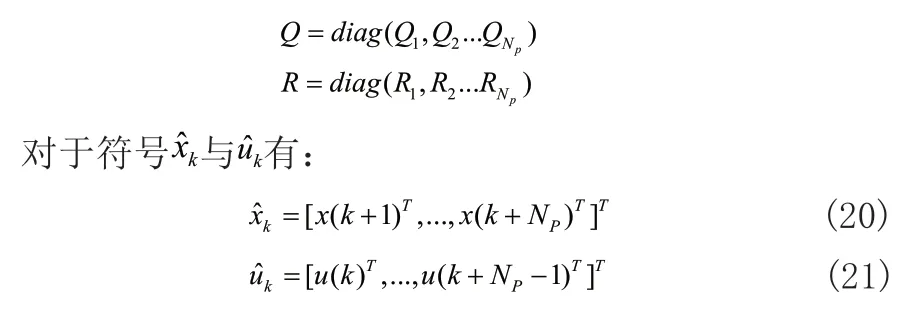
分别是有限时域下的预测状态集合和输入集合，

根据模型(18)进行递推，可以得到如下预测状态与输入之间的关系作为模型预测控制的基础：

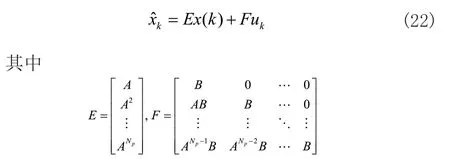
通过将预测状态与输入之间的关系(22)代入到目标函数(19)中，原目标函数可以消除预测状态，并用如下的只包含预测输入的函数表示：其中H=(FTQF+R)，M=(FTQEx(k))T。CONSTANT表示一个与无关的常数。

3 快速模型预测控制方法

3.1 无约束情况

值得一提的是，在工程上，通常情况下，在经过辨识后已经得到了系统的工作点附近模型后，系统在工作点附近运行时，使用模型预测控制算法往往不对模型进行修改。通过观察式(22)可以发现，当模型不改变时，F矩阵在预测过程中保持不变。此外，如果在MPC上线运行前固定好权重系数Q和R，且在计算过程中不对其做更改，则同时可以通过推导发现MPC目标函数(19)中的Hessian矩阵H保持不变。

根据上述观察以及推导得到的信息，下面进行基于奇异值分解的快速MPC方法的简要介绍。首先计算Hessian矩阵H的共轭向量集P，P满足：

其中P是Hessian矩阵的SVD分解得到的共轭矩阵，σi是Hessian矩阵的特征值且满足：

通过使用P，对输入进行线性变化，可以将输入投影到一个新的空间：

此时，原目标函数(19)可以通过使用式(26)转化为与相关的共轭空间形式：

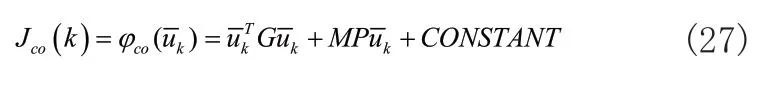
当MPC运行过程中不存在约束的情况下，上述共轭空间目标函数(11)的最优无约束解可以直接通过下面的等式获得：

此时，可以紧接着使用式(28)便捷地从共轭空间解获得实际空间中的无约束最优解。

3.2 有约束情况

上一节是在无约束情况下进行的计算，然而，在工业生产实际过程中，系统往往存在着各式各样的约束，MPC运行过程中需要将全部约束纳入考虑从而保障设备安全稳定运行。同式(22)一样，通过使用式(18)，系统约束可以表示为uˆk相关的不等式：

则在线MPC解决的优化问题如下：

在无约束情况下，无约束解是计算得到的最优解，然而系统约束存在时，无约束解的直接应用势必会造成输入或输出约束违反，长此以往将不可避免地对设备造成一定程度的损坏，并最终影响系统的安全性，引发工业生产事故。然而，直接丢弃掉无约束解信息，重新对新的优化问题(19)进行计算，又没有对可用信息进行合理利用，增大了在线计算时间。如果合理地设计一个方案合理利用共轭空间的无约束最优解，以在不求解优化问题的情况下获得一个满足约束条件的次最优解，则可以大大缩短在线计算时间。

想要利用无约束解信息，最简单且直观的方法是无约束解中使得约束违反的部分移动到其边界上，然而，这种粗暴的方式往往会使得获得的解控制性能极差，根本达不到所需要的控制效果。为此，设计了一种新的约束存在下的方案，所设计的方案被称为基于奇异值分解的快速MPC方法，其具体方案如下：

为了应用所获得的无约束最优解，首先将经过转化后的目标函数(27)重新写为：

为了充分利用共轭空间无约束最优解，我们基于上述分析，给出了一种次优解的线性搜索方式：

根据特征值大小顺序按照特定规则将其对应的共轭空间无约束最优解元素依次置为零（即先处理最大特征值对应的元素，如果不满足约束，再将第二大特征值对应元素置0），直到约束条件达到满足。定义此时的元素编号为r，则共轭空间次优解应该存在于Ur与Ur+1之间，其中：

λ需要满足下述关系：

综上，基于奇异值分解的快速模型预测控制方法总结如表1所示。

表1 快速模型预测控制方法 (FMPC)

4 应用研究：超临界机组控制

4.1 工作点线性化模型及实验参数

实验所采用的被控对象数学模型引自参考文献[14]。机组设计额定功率为600MW。根据历史数据进行辨识，其在50%工况下系统的线性化模型如公式组(36)所示。

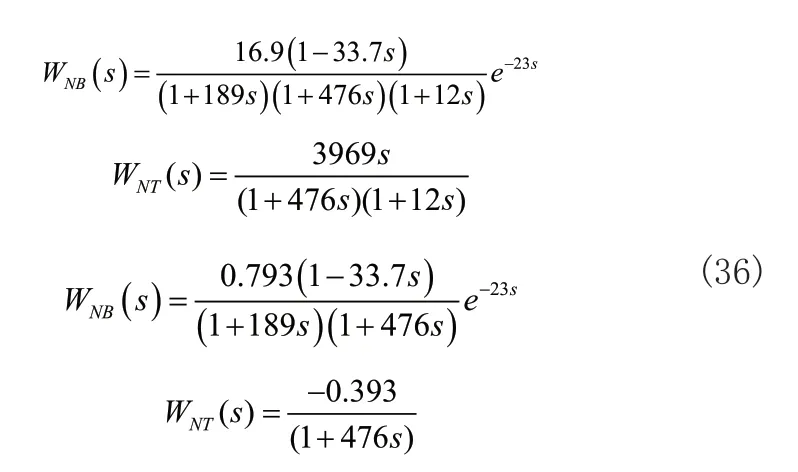
实验过程中算法的其他参数选择如表2所示：

表2 实验参数

此外，为了保障设备安全性，对于本实验施加的约束如式(37)所示：

4.2 实验结果

为了验证所提快速模型预测算法在超临界火电机组应用的有效性与快速性，对超临界火电机组的设定值进行改变并交由算法进行跟踪。将机组功率输出改变设定值为1，并维持机前设定值为0，进行仿真实验，使用FMPC与使用MATLAB内置函数（quadprog内点法求解二次规划）得到的仿真对比结果如图1～图4所示。

图1 功率设定值跟踪变化

图2 压力设定值跟踪变化

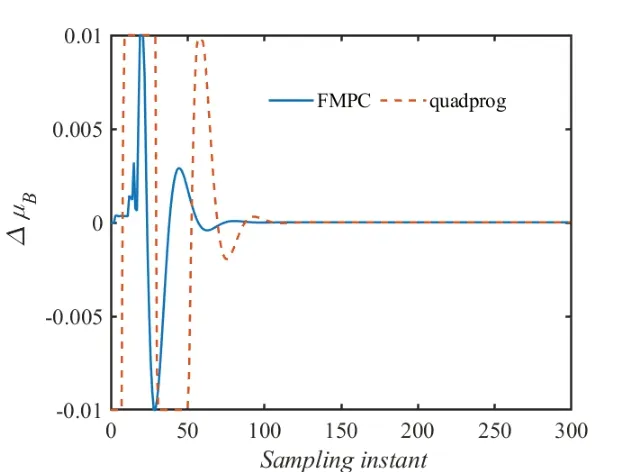
图3 燃料指令增量变化

图4 汽轮机调门开度增量变化

可以看到两种算法均能够快速地跟踪到给定的设定值，且都可以将变量控制在约束范围之内。

FMPC两种算法的在线计算时间对比结果如图5所示。

图5 快速MPC算法与内点法时间对比

可以看到，快速MPC方法相较于内点法，单次采样时间内在线计算时间更短（约为内点法的二分之一），验证了所提算法的快速性与有效性。

5 结语

随着科学技术的发展，超临界机组已经逐渐在火力发电市场中崭露头角。本文首先搭建了超临界机组的机理模型，并推导得到超临界机组工作点附近的线性模型。考虑到超临界机组的非线性特点，以及工业生产过程中对于时效性的考量，设计了可以应用于机组的快速模型预测控制算法。随后以某660MW单元机组为例，选取50%负荷条件下，在MATLAB使用所提出的快速模型预测控制算法对超临界机组进行仿真控制，结果表明所提方法在保障了控制效果的同时，相较于传统内点法具备更短的在线计算时间。