基于Copula聚类模型股票市场VaR度量

□文/刘明成

（1.重庆工商大学数学与统计学院；2.社会经济应用统计重庆市重点实验室 重庆）

［提要］对股票分组引入聚类分析，通过对股票收益率的分析完成中央汇金投资机构所持有的20支股票的聚类，建立t-Copula聚类-VaR模型，得出各置信度下的VaR值，且计算出的VaR通过Kupiec似然比检验，由此避免金融产品自身属性对Copula分组-VaR模型的影响，为金融产品投资者提供新的风险价值衡量方向。

一、引言

组合投资一直是金融机构的投资主题，对其聚合风险的评定是一个绕不开的话题。VaR风险度量法在1963年被Baumol提出，现如今已成为风险测量的主流路径，将各种模型结合VaR度量方法能够得到更加精确的风险价值。传统的VaR计算方法包括历史模拟法、方差-协方差法、蒙特卡洛模拟的方法，此种方法已经被秦拯、杨杨等学者探讨研究过，对于衡量单一资产的金融风险有很好的效果，但对于存在复杂相依结构的组合投资有很大的局限性，会忽略多个金融资产之间的联合分布。而Sklar提出的Copula函数，便成为了描述多个金融资产风险之间的相依关系的有利工具，王明哲、鲁志军、曹辉利用Copula-VaR模型将组合投资的整体风险进行了测量，得到了比传统var测量方式更优越的结果。但混业经营下金融机构所拥有的基础金融产品的维度数量庞大，若是单纯地利用一个Copula函数对它们之间的相依关系进行度量，会出现“维数灾难”，而周全、陈振龙在金融机构的混业经营情况下提出分组的Copula-VaR模型在一定程度上有效地缓解了这一问题，但他们两人提出的分组是基于判定金融产品所属类型上，具有一定主观性，而且若是所有产品都属于同一类别也会造成无法“降维”的窘迫情况。为解决这两个问题，本文提出Copula-聚类-VaR分析方法，通过金融收益率之间的相似程度为启发方向进行探索。

二、相关理论及方法

（一）传统风险度量工具VaR的定义。VaR是value at risk（在险价值）的缩写，是进行风险测度的重要工具。其意义是在资产价值波动的情况下，在一定的概率水平下，投资者或金融机构所持有的资产在未来的一段时间内产生最大可能的损失。用公式表示如下：

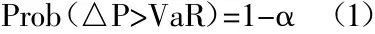
△P为单一资产或是组合资产在持有期内的损失，VaR为执行水平α下的风险价值，而在实际运用中，风险价值的度量往往是通过对数收益率来计算，本文也采用这种方法。

（二）VaR模型的准确性检验。本文采用Kupiec（1995）提出的失败频率检验法进行模型的检验，即假定CoVaR估计具有相互独立性，实际损失超过估计出的CoVaR为失败，否则为成功，p*=1-a（a为置信度）。实际考察天数为T，失败天数为N，那么失败频率为p（N/T）。零假设为p=p*，如此对VaR模型准确性的评估就转化为检验失败频率p是否显著不同于p*。便提出了对零假设最为适合的似然比率检验：

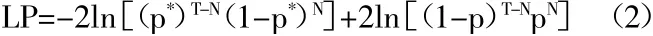
在零假设条件下，统计量LP服从自由度为1的χ2分布。如，当置信度为0.05时，临界值为3.841，若计算出的LR统计量小于这个值，则接受原假设，认为模型通过检验。

（三）K-均值聚类算法。相比于用一个Copula函数去测量整个组合资产的风险价值，Copula分组模型得到的效果更加优良，而对金融序列进行分组是通过其所属的产品和行业的类别来判别，忽略了数据本身的波动情况，所以本文将从多个金融产品的波动率方面进行分类，然后再采用多个Copula模型进行蒙特卡洛模拟得到最后的风险价值。

K-均值聚类算法是动态聚类中历史悠长的典型算法，在1968年由MacQuean提出，在各领域具有广泛的影响力。算法开始时先将要被分类的数据分为K个组，之后随机挑选出K个对象作为聚类中心，由此计算每个数据与K个聚类中心之间的距离，进行临近分配。聚类中心和分给它们的数据对象就形成一个新的类别，由此不断重复直到满足聚类中心不再发生变化时，即误差平方和局部最小，就形成了最终的聚类情况。

（四）copula函数理论。Copula函数的概念最早是由Sklar提出的，其在统计学上的作用是将多个单独的分布函数通过Copula函数作用成一个联合分布。

1、Copula函数定义。d维Copula函数C是指有如下性质的一类多元函数：

·C对它的每个变量都是单调增加的；

·C（u1，…，uk-1，0，uk+1，…，ud）=0且C（1，…，1，uk，1，…，1）=uk，其中u1，…，ud∈［0，1］。

所以，存在一个具有边缘分布F1，…，Fd的d维联合分布函数F，则有一个Copula函数C，使得：

F（x1，…，xd）=C（F1（x1），F2（x2），…，Fd（xd）），-∞≤x1，…，xd≤+∞成立。

2、Copula函数。目前已经出现了多种Copula函数，可大致分为椭圆Copula和Archimidean Copula两类，而椭圆Copula函数根据随机变量所服从的具体分布可分为多元正态Copula和t-Copula。

由于金融数据的尖峰厚尾性，本文不妨将各金融数据拟合成t分布，利用t-Copula函数进行组合资产的风险价值的测量。t-Copula满足下式：

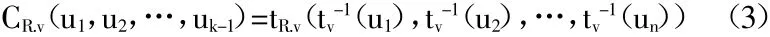
上式中，tR.v（·）为自由度是v的相关系数矩阵为R的多元t分布，tv-1（·）为自由度是v的t分布函数的逆函数。

其分布函数和密度函数分别为：

其中，参数可以由两阶段法的极大似然估计求出，即先估计出各边缘分布的参数，确定边缘分布后，代入收益率数据进行（0，1）之间的映射，再由映射后的数据得出Copula函数的参数。

（五）基于Copula的蒙特卡洛模拟。使用蒙特卡洛模拟的算法，生成大量随机的收益率数据，再利用VaR定义确定置信度下的风险价值。其具体步骤如下：（1）确定各组内各收益率的边际分布；（2）通过映射的数据确定各组Copula函数的参数，由此确定各组的Copula函数；（3）利用拟合好的Copula函数生成大量的随机数；（4）将上一步生成的随机数通过边缘分布函数的逆得出相应的收益率；（5）将得出的收益率以等权重的方式求和计算不同置信度下的VaR值。

三、实证分析

为满足研究方向的潜在条件，即所有的股票是都被同一家机构所持有。故选择中央汇金资产管理公司所投资的20支股票进行研究，数据来源于东方财富choice金融终端，时间段为2015年6月1日至2021年3月23日的日收盘数据，去除缺失值后，数量为948，股票名称及类别如表1所示。（表1）

表1 股票分类及名称一览表

之后，通过利用对数收益率公式：

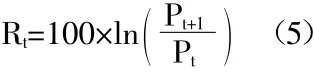
计算出每只股票的波动率，再进行K-均值聚类，这里是将每支股票作为样本，将其每天的收益率作为特征进行计算，得到了聚类的数量为5组，由此产生新的分组。聚类的结果如表2所示。（表2）

表2 聚类后样本分类情况一览表

由此我们完成了对收益率情况相似的股票进行划分。然后，将各收益率数据拟合成t分布，计算出所有边缘分布函数的参数，之后每一组边缘函数都由一个t-Copula函数进行连接，再估计出各组的参数（ρ，v），其中（ρ，v）分别表示t-Copula函数的相关系数和自由度，其结果如表3所示。（表3）

表3 参数估计情况一览表

通过估计出的5组参数，可以得出5个t-Copula函数。接着采用蒙特卡洛模拟的方法，对每一组t-Copula函数随机生成出5组共20支股票的50，000个收益率，接着按每支股票权重相等的方式进行简单平均计算，得到组合资产的总收益率。然后按照风险价值的定义找出置信度为1%、2.5%、5%相应的VaR值，并且计算出各自的LR统计量以检验模型是否通过，结果如表4所示。（表4）

表4 置信度对应的VaR一览表

由表4可知，在1%、2.5%、5%三个置信度情形下，其收益率的损失大小分别为10.819%、5.08%、2.96%，其含义是在越极端的情况下，其损失的价值越大。相应的LR统计量都小于相对应的χ2（1）值，即结果通过了Kupiec似然比检验。

四、结论

基于资产类型分组之后再利用Copula函数进行VaR值计算的方式虽然被人提出，但却需要对金融产品的类型或者按产品所属行业进行分组，忽略了数据本身衍生出的收益率波动情况，而本文表明，针对各产品收益率的波动情况进行聚类分组，再进行Copula-VaR计算从理论与实际操作两个方面都是能够完成的。这样可以为投资者提供新的风险衡量方向，进一步完善了风险价值测量方法。