一类互不相交的整数集合*

孙营营

(菏泽学院数学与统计学院,山东 菏泽 274015)

引言

数集的渐进密度是数论研究的重要课题，几何级数是研究数集相关问题的重要工具[1-3].2013年，Nathanson在文献[3]中用两组长度为k的几何级数集合

X(a)={3k-1a,3k-25a,…,3k-1-i5ia,…,5k-1a}

(1)

Y(b)={5k-1b,5k-27b,…,5k-1-i7ib,…,7k-1b}

(2)

注 本文中出现的小写字母如不加说明都表示正整数．

本文给出较式(1)、(2)更一般的集合，得到他们在各种限制条件下的关系，可用于几何级数相关的整数问题的研究.

1 定理及证明

定理1给定正整数m，对任意的正整数l和奇数a，令

Al(a)={2(l-1)ma,2(l-1)m+1a,…,2(l-1)m+j,…,2lm-1a}

(3)

则Al(a)是一组两两不相交的整数集合.

证明令Al′(b)={2(l′-1)mb,2(l′-1)m+1b,…,2(l′-1)m+j,…,2l′m-1b},其中l′是正整数，b是奇数，且l≠l′,a≠b至少满足一个.

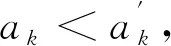
若Al(a)∩Al′(b)≠∅,则存在0≤i,j≤m-1，使2(l-1)m+ia=2(l′-1)m+jb，即

当a=b时，由l,l′,i,j是整数知，上式右端指数部分(l′-l)m+(j-i)=0，此时l=l′，这与l≠l′,a≠b至少满足一个矛盾.

当a≠b时，由l,l′,i,j是整数知，上式右端是一个偶数或偶数的倒数，这与a,b是奇数矛盾.

所以Al(a)∩Al′(b)≠∅.

因此Al(a)是一组两两不相交的整数集合.证毕.

定理2给定正整数m以及足够大的正整数n，令

(4)

式中ak是整数，满足

(5)

以及

(6)

这里pk是指第k个素数.Sk(ak)是一组互不相交的整数集合.

证明由Bertrand假设[5]知任意相邻的素数满足pk+1<2pk，所以当pk确定后，只要n足够大，总有满足(5)式的ak.又pkak+1.

下面分两部分证明(4)式所定义的集合是互不相交的.

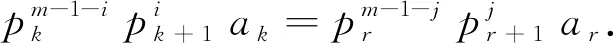
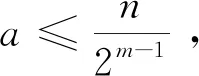
证明当l≠1时，定理1中的集合是偶数集，而定理2中的集合都是奇数集，显然二者交集为空.

2 应用

在上述定理结论中取确定的素数，能够得到一些具体直观的集合，这些集合可用于研究不含m项几何级数的集合的密度上界问题．为方便表述，将整数集合{1,2,…,n}的所有不含长度为m的几何级数的子集所构成集合记作GPFm(n).

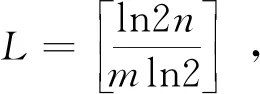
a2≡1,3,7,9(mod 10).

由定理1 、2、 3知Al(a),S3(a3),S4(a4)是三组互不相交的整数集合，由定理3知Al(a),S2(a2)互不相交，另外易证S2(a2)，S3(a3),S4(a4)也是互不相交的，因此Al(a),S2(a2),S3(a3),S4(a4)是四组互不相交的整数集合.

满足条件的Al(a),S2(a2),S3(a3),S4(a4)个数分别为

(7)

(8)

(9)

(10)

如果整数集合Gm∈GPFm(n)，那么Al(a),S2(a2),S3(a3),S4(a4)中每个集合至少有一个元素不属于Gm.由(7)～(10)式得

这里|Gm|表示集合Gm中元素个数.

那么Gm的上渐进密度Du(Gm)满足

这一结果是对Nathanson在文献[3]中给出上界的改进.

3 结语

利用奇数和偶数的互不相交性或者利用素数与整除的性质并按照一定的规律构造可以得到一些互不相交的整数集合.本文借助等比级数以及素数相关的整除性质构造了一系列互不相交的整数集合，对这些集合的互不相交性给出了证明.文中定理所给出的是一般性的结论，对定理中的字母赋值可以得到一些具体直观的互不相交整数集,并对所得集合数目进行计数，这样的具体结论可以用于整数密度相关问题的研究.