基于学生行为数据的学生心理健康状态预测
2022-12-10杨华民底晓强梁钟予张兴旭
杨华民, 于 志, 底晓强, 梁钟予, 张兴旭
(长春理工大学 a. 计算机科学技术学院; b. 吉林省网络与信息安全重点实验室; c. 信息化中心, 长春 130012)
0 引 言
近年来, 大学生的心理健康得到了社会各界的普遍关注。然而, 大部分学生对心理障碍的认识较为模糊, 主动就诊率较低且存在部分学生随意填写心理调查问卷, 导致心理调查问卷不能如实反映学生的心理健康状态[1]。因此如何高效准确地发现存在心理健康问题的学生并进行及时干预与疏导是非常必要的。随着高校信息化的发展, 学生在校内的行为逐渐被数据化, 保存在数据库中, 这为排查有心理健康问题的学生提供了数据基础。基于校园大数据的学生心理健康预测可避免传统方法的抽样误差、 环境约束导致的数据采集偏差等问题, 还可大幅提高效率, 降低成本, 并从多维度、 多视角展现学生的行为属性与个性特征, 实现评价的公正性、 效率性以及真实性。
笔者利用某校学生日常行为数据以及学生开学一个月后测评的《大学生人格问卷UPI》(以下简称问卷)结果数据, 分析学生日常行为与心理健康状态的关系, 其中学生日常行为数据包括学生消费和上网数据, 提取时间范围为学生开学至学生进行心理测评期间, 学生心理测评问卷结果数据包括心理状态正常和异常两种结果。
目前有关心理健康的研究主要关注两个方面, 一个是心理问题的文本分析与治疗, 另一个是关注心理健康的影响因素分析及预测。针对第1方面的研究, Chen等[2]收集了精神分裂症群体、 抑郁症群体以及心理健康群体等299人的语音数据, 并基于该数据集提出了一种基于嵌入式混合特征堆叠稀疏自编码器集成的心理健康语音识别算法, 实验结果表明该算法可根据患者语音准确地对不同心理状态的群体进行分类; Ahmed等[3]基于心理患者的文本描述提出了一种基于可解释注意力网络的深度自适应聚类模型, 实验结果表明该方法有助于标记文本并提高对精神障碍症状的识别率; Li[4]基于人工智能在线技术设计了心理健康教育系统, 可方便快捷地根据心理患者的文本描述信息查询日常心理问题, 并且提供智能在线心理咨询, 以帮助患者克服心理问题。
针对第2方面的研究, Chen等[5]基于认知计算, 结合来自中国和美国不同地区学生的症状自评估量表(SCL_90), 社会评级规模和健康认知问卷(HCQ-127)测试数据分析心理健康的影响因素, 研究表明发达地区的学生更容易产生心理问题。Zhou[6]采用1 264名中国贵州大学新生的症状自评估量表(SCL_90)数据, 使用决策树C4.5算法对大学新生心理健康状况进行分类, 分类结果表明, 躯体化和敌意是影响学生心理健康的重要因素。Liu等[7]基于学生心理、 个人基本信息和社会经济等数据应用BP(Back Propagation)神经网络预测学生的心理问题, 实验结果表明该方法的预测精度较高, 可有效预测学生的心理问题。
然而, 这些研究都未考虑行为与心理健康的关系。但校园大数据为心理学研究提供了新的契机, 随着高校信息化的建设发展, 学生的日常行为数据都以记录的形式逐条保存在学校信息化部门的数据库中, 基于这些日常行为数据, 并利用相关机器学习和深度学习方法, 可以实现心理学的预测和干预。笔者基于学生行为和学生心理测评结果数据, 首先使用自定义公式法进行相关学生行为特征提取, 然后应用Jenks Natural Breaks算法对所提取的特征数据进行标签化, 并应用Apriori算法分析学生行为特征与学生心理健康状态的关系, 最后基于特征分析结果利用所提出的PDNN(Particle Difference Neural Network)神经网络模型预测学生的心理健康状态。
1 多维度学生行为特征提取及特征关联分析
笔者使用学生一卡通中的消费数据、 网管系统中的上网数据等学生日常行为数据进行研究。其中消费数据包括学号、 商家账户、 消费时间、 消费地点、 账户余额以及消费金额等信息; 上网数据包括学号、 登录和登出时间、 总流量以及上网时长等信息。所用的学生行为数据集的基本统计信息如表1所示。

表1 学生行为数据集的基本统计信息
1.1 多维度学生行为特征提取
1.1.1 学生消费特征提取
消费行为是学生日常行为的重要组成部分, 学生的心理健康状态可能会影响其在校的消费行为[8], 因此笔者对学生的消费数据进行特征提取以探究其与学生心理健康状态的关系。
1) 饮食规律性。在探究饮食规律性时, 将每日3餐按30 min的间隔划分时间区间, 统计学生在每个时间区间内的消费次数, 利用信息熵的计算公式, 得到学生的饮食规律性。每日3餐开放和关闭时间经询问食堂窗口相关人员, 划分结果如表2所示。

表2 3餐的时间区间划分
学生饮食规律性计算公式为
(1)
其中D为学生在食堂进餐使用校园卡付款的天数,Td为统计的总天数,pi为学生在各个时间区间的消费频率,n为所划分的时间区间数量。
2) 勤奋性。笔者将学生每天第1次校园卡消费记录作为他们的第1项日常活动。由于食堂的用餐消费占所有消费记录的绝大部分, 因此计算了每个学生每天第1次用餐刷卡的时间, 然后将其作为衡量学生勤奋水平的标准。从而改变原始日期时间格式将其转换为Unix时间戳。因此, 学生勤奋性SDG的计算方法为

(2)
其中T为学生刷卡消费的总天数,tj为学生在第j天第1次用餐刷卡的时间。
3) 共餐人数。假设如果两名同学在同一班级, 吃饭时在同一楼层食堂窗口刷卡消费且刷卡间隔时间小于120 s, 则视为在一起吃饭。笔者统计了每个学院在各校区每个食堂窗口的学生共餐人数情况, 为防止部分同学通过手机支付、 定外卖或去外面吃饭对实验结果造成的影响, 将一个月内在食堂刷卡消费次数低于30条记录的同学移除, 之后将每个食堂窗口得到的统计结果根据学生学号对应相加, 进而得到最终的结果。其中在一个食堂窗口所有学生与其同班同学一起进餐的人数统计流程如下。
算法1 学生共餐人数计算流程。
输入: 学生消费数据集C, 食堂窗口编号N和与N对应的该层的食堂窗口编号列表Nlist。
输出: 所有学生与其同班同学在该食堂窗口一起进餐的人数列表。
1) 根据学生消费数据集C获取班级列表major_class;
2) 循环遍历班级列表获取一个班级的同学stu_major, 并根据消费日期得到该班同学的消费月份month;
3) 循环遍历month列表, 获取该班学生在某个月份的消费记录stu_month;
4) 循环遍历stu_month获取一个学生在当前月份的消费记录stu_one;
5) 判断stu_one长度是否大于等于30, 如果大于等于30, 循环遍历stu_one, 得到食堂窗口编号等于N的消费数据, 转换其消费时间为Unix时间戳, 存入timestmp_1列表;
6) 获取除了该生以外的该班其他学生在与食堂窗口N所对应的该层食堂窗口Nlist的消费数据集, 将所获取到的消费数据集中的时间转化为戳列表timestmp_2;
7) 循环遍历timestmp_1列表和timestmp_2列表, 如果timestmp_1中的时间戳与timestmp_2中的时间戳相差小于等于120, 则计数器count加1;
8) 将count存入学生与其同班同学在食堂窗口N一起进餐的人数列表consume_num, 并将count置0, 转至步骤3), 直至所有循环执行完成。
1.1.2 学生上网特征提取
研究表明, 学生的心理健康状态与网络成瘾水平具有一定的相关性[9], 因此提取学生上网的相关特征以探究学生心理健康状态与其上网习惯的关系。
1) 工作日及周末平均上网时长。考虑到学生在工作日和周末的上网习惯不同, 因此将工作日和周末区分开提取学生的上网特征。学生每次的上网时长可由学生上网记录数据集获得, 学生工作日或周末平均上网时长

(3)
其中T为学生在工作日或者周末上网次数,Ii为学生每次上网花费时间,Td为统计天数。
2) 工作日及周末平均上网最晚下线时间。学生工作日或周末平均上网最晚下线时间指学生在工作日或周末最后一次登出校园网系统的时间平均值, 如果该日学生零点之前还未下线则将第2天最早下线时间作为当天最晚下线时间。将学生登出校园网的时间转换为Unix时间戳的形式, 学生工作日或周末平均上网最晚下线时间
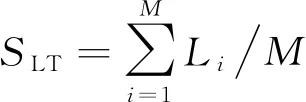
(4)
其中M为统计天数,Li为学生在工作日或周末每天最后一次登出校园网系统的Unix时间戳。
3) 工作日及周末日均使用流量数。学生工作日或周末日均使用的流量数的计算公式为

(5)
其流量单位为MByte。其中n为使用流量的总次数,Fi为每次使用流量所消耗的流量数,d为使用校园网流量的天数。
1.2 特征关联分析
为探究心理健康与心理异常学生群体在相关行为上的差异, 首先应用Jenks Natural Breaks算法对上述提取的特征数据进行标签化。Jenks Natural Breaks 算法又称为自然间断点分级法, 核心思想与聚类一样: 使每组内部的相似性最大, 而外部组与组之间的相异性最大[10], 然后应用Apriori算法分别挖掘心理健康和心理异常学生群体的行为特征标签化数据集, 并设置最小支持度阈值为0.5, 最小置信度阈值为0.5, 所得强关联规则如表3所示。

表3 Apriori算法产生的强关联规则
由表3可知, 心理异常学生群体通常呈现饮食较不规律、 较不勤奋、 共餐人数较少、 上网时长较长且使用流量数较多、 工作日上网下线时间较晚的特点; 而心理正常学生群体通常呈现饮食较为规律、 较为勤奋的特点。
2 PDNN模型的构建
BP神经网络的性能很大程度上取决于BP神经网络的层间权重, 如果初始化层间权重出现偏差, 网络则会出现易陷入局部极小值以及收敛速度慢等问题。因此, 为解决神经网络层间权重选取不精准的问题, 笔者基于改进的粒子群优化算法, 构建了PDNN(Particle Difference Neural Network)神经网络模型, 以此动态选取BP神经网络的层间权重, 进而根据学生行为实现对学生心理健康状态的预测。以两层隐藏层, 每层结点数都为5的BPNN(Back Propagation Neural Network)模型为例, 给出PDNN模型的总体结构如图1所示。其中w1、w2和w3为输入层与隐藏层1、 隐藏层1与隐藏层2、 隐藏层2与输出层之间的权值矩阵, 该权值矩阵应用改进的粒子群优化算法动态获取。对应于图1中PDNN模型的每个粒子构造如图2所示。
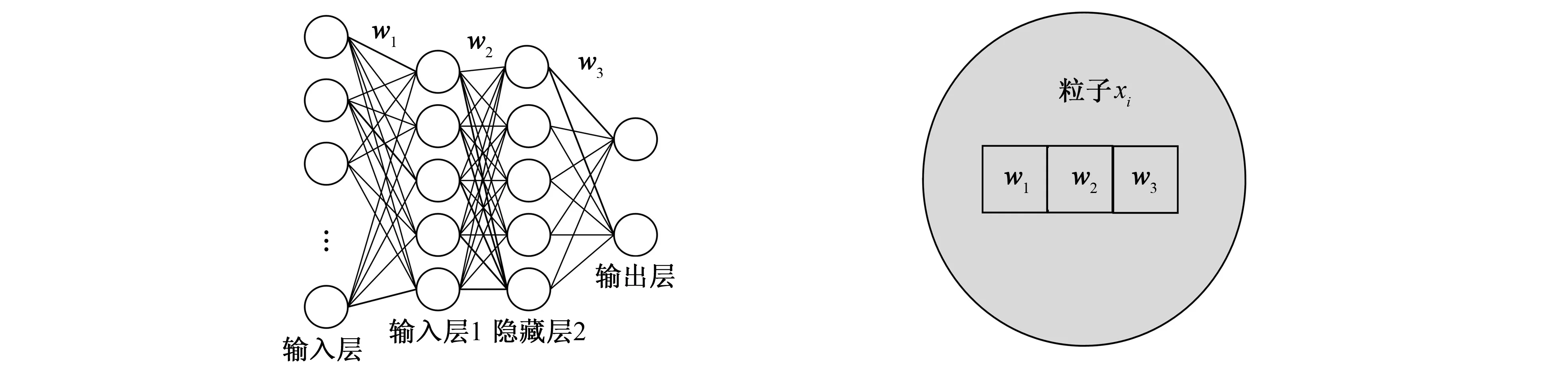
图1 PDNN模型结构 图2 粒子基本结构 Fig.1 PDNN model structure Fig.2 Basic structure of particles
2.1 粒子群优化算法
粒子群优化(PSO: Particle Swarm Optimization)算法源于人类对鸟类捕食行为的研究[11], 该算法基于从环境中获得的适应度信息, 通过粒子群迭代寻找问题的最优解, 粒子在迭代过程中利用局部最优解与全局最优解调整迭代速度与粒子位置, 以更新粒子群[12]。目前粒子群优化算法已被广泛应用于求解如路径规划、 优化调度、 参数辨识、 图像分割等实际优化问题[13]。
假设一组粒子在d维搜索空间中以一定的速度飞行, 则粒子i的当前位置为Xi=(xi1,xi2,…,xid), 当前速度为Vi=(vi1,vi2,…,vid)。粒子i所经历过的最优位置为Pi_best=(Pi_best1,Pi_best2,…,Pi_bestd), 整个粒子群搜索到的最优位置为Gbest=(Gbest1,Gbest2,…,Gbestd)。因此粒子i的速度与位置更新公式为
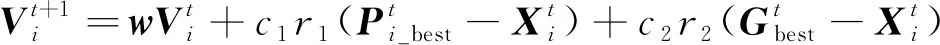
(6)

(7)
其中w为惯性权重,Vi为当前粒子速度,c1为认知系数,c2为社会系数,r1和r2均为[0,1]之间的随机数,t为当前迭代次数。
2.2 改进的粒子群优化算法
2.2.1 惯性权重的改进
在粒子进行搜索过程中, 较大的惯性权重有利于对整个搜索空间进行探索, 并增加群体多样性, 而较小的惯性权重则会提升种群的局部开发能力。因此, 惯性权重是平衡粒子群局部搜索和全局搜索的关键因素, 惯性权重的选取对算法的优化效果具有一定的影响[14]。笔者结合惯性权重线性递减和惯性权重非线性递减方法[15], 提出了动态惯性权重, 其公式为

(8)
其中wmax为惯性权重的最大值,wmin为惯性权重的最小值,t为当前迭代次数,T为最大迭代次数, rand为产生随机数函数。
图3给出了线性惯性权重、 非线性惯性权重以及动态惯性权重随迭代次数的变化图像, 其中线性惯性权重和非线性惯性权重的公式为

(9)
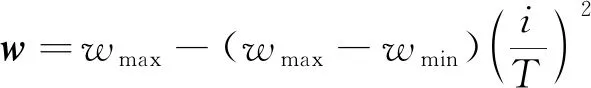
(10)

图3 不同的惯性权重对比Fig.3 Comparison of different inertia weights
如图3所示, 对线性惯性权重, 当开始迭代时, 线性惯性权重值较大, 粒子的速度也较大, 此时粒子具有较好的全局搜索能力。随着迭代次数的增加, 线性惯性权重的值越来越小, 粒子的速度也越来越小, 此时粒子具有较好的局部搜索能力, 但由于斜率恒定, 所以速度的改变总是相同的。如果迭代初期没有产生较好的初始值, 则随着迭代次数的增加以及速度的迅速衰减最后很可能导致粒子陷入局部最优解。对非线性惯性权重, 虽然其斜率相比于线性惯性权重下降较慢且斜率不断改变。但随着迭代次数的增加, 其惯性权重始终维持在一个较高水平, 不利于粒子的局部搜索。虽然在迭代后期惯性权重有所降低, 但仍难以找到全局最优解。对动态惯性权重, 在迭代初期, 惯性权重取得较大的值并随着迭代次数的增加逐渐下降, 有利于粒子对整个搜索空间进行探索。在迭代后期, 惯性权重快速减小, 有利于增强粒子的局部搜索能力。此外, 动态惯性权重随着迭代次数的增加不断发生改变, 可有效避免线性惯性权重或非线性惯性权重随着迭代次数增加容易陷入局部最优解或难以找到全局最优解的情况。综上所述, 笔者提出的动态惯性权重可以平衡粒子的全局搜索与局部搜索, 并且其权重随着迭代次数的增加而交替改变, 满足粒子在搜索过程中的复杂性以及快速收敛性。
2.2.2 劣势粒子的识别
劣势粒子是造成整个粒子群无法获取全局最优解的主要原因, 识别劣势粒子并对劣势粒子进行处理使其跳出局部最优解, 可以有效优化种群的寻优。结合全局最优粒子位置和个体历史最优粒子位置, 引入pinf参数对劣势粒子进行识别,pinf的定义为

(11)
其中ba(i)为粒子a在第i次迭代下的历史最优位置,g(i)为粒子群在第i次迭代下的全局最优位置,f为适应度函数。如果pinf<10-4, 则表示该粒子陷入了局部最优解, 识别其为劣势粒子; 如果pinf>104, 则表示全局最优解暂无更新, 若pinf=NAN, 则表示整个种群陷入了局部最优解, 对以上两种情况, 则识别整个种群的粒子为劣势粒子, 对整个种群的粒子进行变异处理。
2.2.3 劣势粒子的变异
受差分进化算法[16]的思想启发, 对识别出的劣势粒子进行变异。粒子的变异公式为
XVi,g=Xr1,g+F(Xr2,g-Xr3,g)
(12)
在粒子变异过程中, 随机选取当前迭代次数下的3个不同的粒子, 通过变异公式, 得到新的变异粒子, 以帮助劣势粒子跳出局部最优解, 继续寻优。其中Xr1,g、Xr2,g和Xr3,g为当前迭代次数下的3个随机粒子,F为变异率。
2.2.4 粒子的选择
在对劣势粒子进行变异后, 计算原粒子和变异后粒子的适应度函数值, 如果变异后的粒子的适应度函数值小于原粒子的适应度函数值, 则将变异后的粒子放入到下一代粒子种群中。否则将原粒子放入到下一代粒子种群中, 并更新粒子的个体历史最优值和最优位置, 粒子群的全局最优值和最优位置。
2.2.5 萤火虫扰动策略
受萤火虫算法[17]启发, 假设全局最优解为最亮的萤火虫, 其他的粒子为较暗的萤火虫, 根据萤火虫算法思想, 较暗的萤火虫会朝着较亮的萤火虫移动。因此整个萤火虫种群都会朝着最亮的萤火虫移动, 使粒子群逐渐向全局最优解方向靠拢。而全局最优解根据劣势粒子的识别变异以及选择策略不断更新优化, 进而使整个粒子群向优化问题的最终全局最优解收敛, 加速粒子寻优。其粒子群位置更新如下
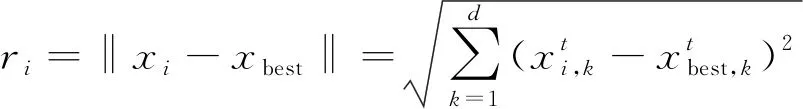
(13)

(14)

2.3 PDNN模型
该模型的构建过程如下。
1) 根据数据集的特征数目确定神经网络的拓扑结构, 搭建神经网络模型。
2) 初始化改进的粒子群优化算法的最大迭代次数max_iter、 当前迭代次数i=1、 粒子变异率F、 粒子总数和粒子结构,并设定粒子速度范围和位置范围。
3) 初始化粒子的历史最优位置, 应用BP神经网络的损失函数作为适应度函数初始化粒子历史最优值, 利用粒子群的最小历史最优值初始化粒子的全局最优值, 使用粒子群的最小历史最优值对应的粒子位置初始化粒子群的全局最优位置。
4) 根据式(11)识别劣势粒子, 如果满足pinf>104、pinf<10-4或pinf=NAN条件则根据式(12)对劣势粒子进行变异处理, 帮助其摆脱劣势, 继续寻优。
5) 根据式(6)~式(8)更新粒子速度与位置。
6) 根据适应度函数值对原粒子和变异后的粒子进行选择。
7) 根据式(13)和式(14)加速粒子群向全局最优解收敛。
8) 更新粒子历史最优值与历史最优位置、 更新粒子全局最优值和全局最优位置, 迭代次数i=i+1。
9) 若i≥max_iter, 则转至步骤10); 否则, 转至步骤4)。
10) 得到全局最优位置, 封装BP神经网络的权值矩阵, 应用该权值训练BP神经网络, PDNN模型构建完成。
3 实验方案与实验结果
3.1 实验方案
笔者选取特征关联分析得到的强关联规则特征数据进行实验, 选择70%的数据用于训练模型, 30%的数据用于测试模型, 实验评价指标采用加权平均, 权重为每个类别样本数量在总样本中的占比。在改进的粒子群优化算法中设置粒子数量为5, 粒子群的最大迭代次数max_iter设为50, 惯性权重的最大值为0.9、 最小值为0.4, 粒子的变异率为0.6, 基于Eberhart的理论[18], 将认知系数c1和社会系数c2设为区间[1.494 45, 2]中的随机数, 粒子的速度范围设为-3≤v≤3, 粒子的位置范围设为-1≤p≤1, 粒子速度和位置的初始值均为[0,1]区间内的随机数。为避免不同特征数据的数据范围不一致对模型性能的影响, 在实验前需要对特征数据进行标准化, 选取最大最小标准化方法对特征数据进行标准化, 使每个特征数据的范围均落在[0,1]区间内。最大最小标准化方法为

(15)

3.2 实验评测指标
实验评测指标采用准确率(a)、 精确率(p)、 召回率(r)以及F1分数(F1), 其表达式为

(16)
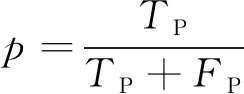
(17)
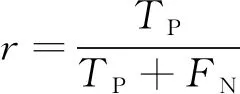
(18)
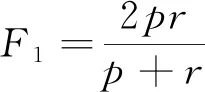
(19)
其中TP为预测值为正, 实际值也为正的样本数量;FP为预测值为正, 实际值为负的样本数量;FN为预测值为负, 实际值为正的样本数量;TN为预测值为负, 实际值也为负的样本数量。
3.3 实验结果
为避免模型对数据集划分的依赖性, 每次实验选择不同的测试集和训练集。具体过程, 将数据集按从前到后的顺序平均划分为10份, 假设每份的标号分别为1、2、3、…、9、10, 则第1次实验将选取1~7份作为训练集, 其余作为测试集。第2次实验将选取2~8份作为训练集, 其余作为测试集。以此类推, 直到取完第10次划分为止, 然后取每个评价指标的平均值。实验选用的对比模型为: Nave Bayes、 SVM(Support Vector Machines)、 逻辑回归(LR: Logistic Regression)、 BPNN(Back Propagation Neural Network), 各模型的实验结果如表4所示。

表4 各模型实验结果
如表4所示, 笔者提出的PDNN模型在4个评价指标中均取得了最优结果, 并且其预测学生心理健康状态的准确率为86%、 F1分数为0.86, 而LR模型的效果最差, 其准确率为82%, F1分数为0.82。
此外, 在模型训练过程中笔者还对比了GA-BPNN(Genetic Algorithm Back Propagation Neural Network)、 IPSONN(Improved Particle Swarm Optimization Neural Network)、 ABC-BPNN(Artificial Bee Colony Back Propagation Neural Network)、 BPNN和PDNN模型随着迭代次数的增加损失函数值的变化。如图4所示, 从图4中可以发现, 在模型训练过程中BP神经网络的损失函数值大于其他模型, 因为智能算法已根据BP神经网络的损失函数值对其进行寻优, 将寻优得到的权值赋给BP神经网络模型进行训练, 因此经过智能算法优化得到的损失函数值小于按BP神经网络权重初始值得到的损失函数值。同时, 从图4中还可以发现, 在模型训练过程中笔者提出的PDNN模型相比于其他模型其损失函数值一直保持最低的状态, 说明提出的改进粒子群优化算法得到的BP神经网络的层间权重可以较好拟合数据, 表明该模型学习能力和泛化能力较强, 可快速收敛并保持着较优的结果。最后, 基于上述对数据集的划分方法, 笔者还对比了GA-BPNN、IPSONN、ABC-BPNN、PDNN模型在各评价指标上的实验结果, 如图5所示。从图5中可以发现, 笔者提出的PDNN模型相较于其他智能算法优化后的神经网络模型, 其效果仍是最优的, 在accuracy、precision、recall以及F1-score等4个评价指标上均取得了最优的结果, 其值分别为86%、87%、86%和0.86, 表明PDNN模型可以根据学生的日常行为更加有效地预测学生的心理健康状态, 以帮助学校及时发现有心理问题的学生, 并进行相关的干预与疏导, 使其重新回到正常的生活和学习, 具有一定的现实意义。

图4 各模型随着迭代次数增加损失函数值的变化图像 图5 各智能优化算法的模型实验结果对比 Fig.4 Change image of loss function value of each model with the increase of iteration times Fig.5 Comparison of model experiment results of various intelligent optimization algorithms
4 结 语
笔者基于学生的日常行为数据预测学生的心理健康状态。首先, 应用自定义公式法进行相关特征提取; 然后应用Jenks Natural Breaks算法和Apriori算法进行特征分类和挖掘, 特征关联分析结果表明, 学生饮食规律性、 勤奋性、 共餐人数、 上网习惯与学生的心理健康状态具有一定的相关性; 最后, 基于改进的粒子群优化算法, 构建了PDNN神经网络模型, 用于预测学生的心理健康状态。实验结果表明, 笔者提出的PDNN神经网络模型相比于其他传统机器学习和相关深度学习模型其准确率较高性能较好并且模型可快速收敛, 更加准确有效地预测学生的心理健康状态, 以帮助学校及时发现心理问题学生并进行相关的干预与疏导。
未来将进一步探究学生成绩以及学生静态特征, 如学生民族、 年龄、 来源省份、 性别等与学生心理健康状态的关系。
