基于改进黏菌算法的配电网重构研究

高金兰, 王良禹, 宋 爽

(东北石油大学 电气信息工程学院, 黑龙江 大庆 163318)

0 引 言

配电网重构实质是通过调整开关的开断组合实现减少损耗, 平衡负载, 提高供电优质性、 安全性、 可靠性和经济性等目标的配网规划方法[1]。配电网保持辐射性和连通性的拓扑结构是求解配电网重构问题的前提条件, 在此基础上, 配电网还需满足诸多约束, 如设备容量以及节点电压等。随着现代网络规模的不断扩展, 重构问题也变得越来越复杂。目前, 求解配电网重构的方法大致分为数学优化算法[2]、 启发式方法[3-4]和智能优化算法[5-8]3类, 其中智能优化算法在求解非线性规划问题上具有优异表现, 因此被广泛使用。

徐渊[9]将布谷鸟和粒子群算法相结合应用于配电网重构问题中, 提高了粒子群算法的全局搜索能力； 董张卓等[10]首先建立配电网的连接模型, 再通过映射规则, 建立起重构和简化图, 同时给出重构图中树支的概率, 得到重构图的最小生成树。王威等[11]提出一种通过网络辐射结构确定最优解的方法, 首先通过生成树确定可行的参考解, 将开关必闭合的原则与Minty算法相结合, 使生成树的数量大幅减少； 黄弦超等[12]首先通过回支关联矩阵, 使配电网始终保持辐射状拓扑网络, 然后根据最优流算法生成最优解以提升寻优效率。然而, 上述方法在保证配电网辐射运行方面仍存在不足, 如在计算含有大量开关的复杂配电网时仍存在大量不可行解, 计算时间不能满足需求； 同时, 在算法优化方面仅在传统算法上进行某一方面的优化, 不能同时兼顾算法的收敛速度和全局收敛能力。

黏菌算法(SMA： Slime Mould Algorithm)[13]是一种源于黏菌捕食行为的智能优化算法, 该算法具有较好的收敛精度和稳定性, 因此已被广泛应用于优化应用领域, 但其缺点是在初始种群基数庞大时收敛速度较慢, 且容易得到区域最优解。因此, 笔者提出了一种基于改进黏菌算法的配电网多目标重构策略。首先, 从配电网的运行效益和负荷均衡度两个角度出发, 建立以有功损耗及网络负载平衡指数最小为目标的配电网重构模型； 其次, 针对黏菌算法(SMA)收敛速度慢、 易得到区域最优解等问题, 在黏菌算法中设置阈值并引入高斯扰动, 加快收敛速度与精度, 引入折射反向学习策略, 解决黏菌算法在中后期容易陷入局部最优的问题； 同时, 为提高黏菌算法的搜索效率, 避免大量不可行解的存在, 将Prim算法与连续支路交换算法结合, 对网络拓扑结构进行优化, 以此作为黏菌算法的初始种群。IEEE33、 118节点系统仿真结果表明, 该方法能以更短的计算时间均衡网络负载, 有效降低有功功率损耗。

1 配电网重构模型

1.1 多目标函数

笔者选择以降低网络总有功损耗和均衡负荷[8]为优化目标。

(1)

2) 网络负载平衡指数Lindex

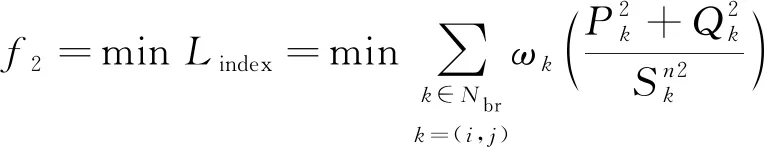
(2)

3) 综合目标函数。对上述目标函数进行归一化处理并构建目标函数, 则有

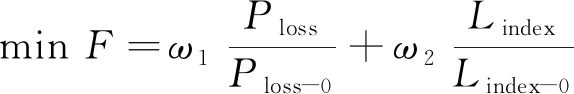
(3)

其中Ploss-0和Lindex-0分别为配电网重构前的有功网损和网络负载平衡指数；ω1和ω2分别为上述两个指标的权重系数。为保证所得解的多样性, 采用将权重随机分配的方式,ωi为0～1范围内的随机生成数, 且ω1+ω2=1。

1.2 约束条件

1) 潮流约束, 需满足

(4)

其中Pi和Qi分别为节点i注入的有功和无功功率；Pdi和Qdi分别为节点i负荷的有功和无功功率；Glj、Blj、δlj分别为节点i、j之间的电导、 电纳和相角差；m为网络中的节点总数；Ui、Uj分别为节点i、j处的电压幅值。

2) 节点电压约束, 需满足

Uimin≤Ui≤Uimax

(5)

其中Ui、Uimin、Uimax分别为节点i处的实际电压及其上下限。

3) 支路容量约束, 需满足

|Sk|≤Skmax

(6)

其中Sk为支路k中流过的功率,Skmax为支路k中允许流过的最大功率。

4) 网络拓扑约束。重构过程中配电网必须保持辐射且连通, 不能存在环路及孤岛。

2 改进黏菌算法

2.1 标准黏菌算法

标准黏菌算法的数学模型为

(7)

其中t为当前迭代次数,Ub与Lb为搜索区域的上下界,r和r1为均匀分布在[0,1]之间的随机数,z为自定义参数,Xb(t)为目前适应度最优的个体位置, 控制参数vb为[-a,a]之间的随机数, 反馈因子vc为从1～0线性递减的参数,Xrand1(t)与Xrand2(t)为两个随机个体位置,W为黏菌的权重系数, 控制参数p、 参数a与权重系数W的更新公式为

p=tanh|S(i)-DF|

(8)

(9)

(10)

SIndex(i)=sort(S)

(11)

其中i∈1,2,3,…,N,N为种群数量,S(i)为当前个体适应度值,DF为所有迭代中的最佳适应度值。r为均匀分布于[-a,a]的随机数,tmax为最大迭代次数。式(11)对适应度值进行排序,SIndex(i)为排序后的适应度值序列, 表示气味指数,C为种群中适应度排在前一半个体,O为剩下的个体,bF为当前迭代获取的最佳适应度值,wF为当前迭代最差适应度值。

2.2 改进黏菌算法

SMA具有多种搜索模式, 适应度较好的黏菌个体集中在最优位置附近, 适应度较差的个体进行全局搜索, 当随机数小于z时, 黏菌进行随机初始化。但在迭代后期,vb的振荡效果明显下降, 使计算不能有效地跳出局部最优, 而且SMA利用参数vc实现收缩机制, 但这种机制比较薄弱, 容易陷入局部最优, 同时, SMA也存在收敛速度较慢的问题。为解决以上问题, 对SMA算法进行了如下改进。

2.2.1 引入折射反向学习策略

针对黏菌算法在迭代中后期容易陷入局部最优的问题, 在算法中融入折射反向学习的思想。反向学习思想是智能算法的一种改进策略, 核心思想是通过当前解产生一个反向解, 比较两者并取最优进入下一次迭代, 以此跳出局部最优区域； 折射反向学习策略(ROBL： Refracted Opposition-Based Learning)是在此基础上结合光的折射原理提出的策略[14], 其原理如图1所示。

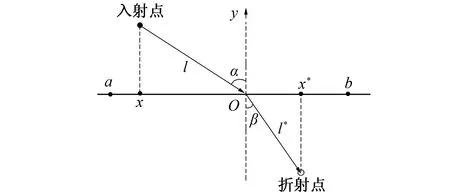
图1 折射反向学习原理图Fig.1 ROBL mechanism

图1中, 已知[a,b]为解在x轴上的搜索区间, 原点O为[a,b]之间的中点,y轴为法线,α、β分别为入射角和折射角,l、l*分别为入射光线和折射光线的长度, 由此可得折射率

(12)

令δ=l/l*, 代入式(12)并将其拓展到D维空间, 可得折射反向解

(13)

2.2.2 设置迭代阈值和高斯扰动

高斯扰动在提高种群多样性、 避免生成区域极值的同时, 也可有效加快算法的收敛速度。因此, 笔者在迭代中设置搜索阈值M, 即首先利用黏菌算法进行全局搜索, 当算法迭代M次的正整数倍时, 将当前种群位置备份, 同时按照当前最优解位置进行局部寻优, 将寻优前后最优解进行比较, 若该结果更优, 则用

(14)

产生p%新个体替换掉原种群中较差的p%个体。对每次迭代生成的最优解根据

pG-best=pbest(1+Gaussian(σ))

(15)

(16)

进行高斯扰动并替换。其中d为种群规模大小,r1、r2为[0,1]中的随机数,yi为新生成个体i的位置,pbest为每代最优解,pG-best为扰动后黏菌的位置, Gaussion(σ)为高斯分布函数。

3 基于改进黏菌算法的配网重构策略

3.1 网络拓扑优化

由于复杂的电网结构使初始种群产生大量不可行解, 缩小种群的初始规模可大幅加快收敛速度、 提高搜索精度, 因此可基于生成树的方法满足辐射型网络的约束条件。连续支路交换算法(SBEA： Successive Branch-Exchange Algorithm)为启发式算法的一种[15], 核心思想是： 从可行的树(父代)开始, 通过依次进行交换分支连续创建新树, 每次交换中在没有违反任何约束的情况下最大程度地改进目标函数, 即交换选择的分支会生成所有可能解中的最优解。但这种搜索方法不能覆盖所有树, 它仅通过父代树作为起始树依次计算, 最终导致的结果是在父代树附近的局部最优解。笔者在此基础上, 将Prim最小生成树[16]算法与SBEA结合, 扩大搜索空间, 同时利用分支交换的核心思想优化初始种群。

3.1.1 混合prim-SBEA算法

首先应用Prim算法确定初始生成树(父代), 将网络中所有联络开关和分段开关都闭合以形成环状网络, 进行Nel-cycles次潮流计算确定功率分布, 公式如下

Nel-cycles=Nbr-(Nbus-NSP)

(17)

其中Nel-cycles为配电网中的回路数,NSP为电源节点数,Nbr为支路数,Nbus为节点数。如果配电网中有多个电源点, 可将它们合并成一个, 从而将最小生成林问题归结为最小生成树问题。对环网进行潮流计算并将分支赋权, 其中每个分支的权重与支路潮流成反比。在避免产生孤岛的同时, 通过对最小生成树应用Prim算法打开集合中权重最高的分支, 可得到初始的辐射状全连接配电网。这可以最大限度地减少孤岛对配电网中正常潮流的干扰, 并保证初始放射状配电网具有良好的潮流模式, 而且系统网损较低。同时, 在使用Prim算法时可得到支路中除树支外的连支集合向量[]Nel-loopx1。

得到连枝向量后, 通过向量[]Nel-loopx1的随机变换生成一个随机向量, 利用SBEA的核心思想进行分支交换处理。例如, 随机向量[b11,b3,…]表示的含义如下： 第1步闭合支路b11的开关形成一个环网, 在这个新形成的回路中寻找更符合目标函数的分支, 如果存在, 则将b11替换为该分支, 否则不进行交换； 第2步闭合支路b3的开关, 在新形成的回路中更符合目标函数的分支, 如果存在, 则将b3替换为该分支； 以此类推, 根据生成的随机向量重复上述过程。

在交换过程中, 利用近似方程计算辐射配电网的潮流可以在短时间内使用SBEA算法生成个体。在文献[15]中给出了网络损耗和负荷均衡度近似线性化的具体计算过程, 不再详述, 公式如下

(18)

(19)

这种近似仅用于总体初始化, 目的是通过启发式算法创建一组初始候选解。该方法使用线性化的解析表达式近似支路交换过程中的网损变化或负荷指标变化。算法中的所有其他步骤(适应度函数、 电压条件和潮流的计算)都使用精确的完全非线性潮流表达式, 再将此过程得到的解与Prim算法单独生成的解进行合并, 作为黏菌算法的初始种群, 目的是为将搜索空间扩大, 避免单一使用Prim算法或连续支路交换算法不能全面覆盖可行解的缺陷。

3.2 算法流程

基于改进黏菌算法的配电网多目标重构方案如下:

1) 将配电网初始化, 输入配电网的原始信息；

2) 应用Prim算法确定初始生成树, 将网络中所有联络开关和分段开关都闭合, 形成环状网络, 进行潮流计算确定功率分布；

3) 进行潮流计算并将各支路赋权, 其中每个分支的权重与支路潮流成反比, 每次打开集合中权重最高的分支, 得到初始的辐射状全连接配电网；

4) 将步骤2)中除树支外的连支集合得到向量[]Nel-loopx1；

5) 通过向量[]Nel-loopx1的随机变换生成一个随机向量, 用支路交换法进行分支交换处理, 将得到的解与Prim最小生成树的解集合成黏菌算法初始种群；

6) 进行黏菌算法的初始化, 设置初始黏菌种群数量N, 研究问题维度D, 最大迭代次数Tmax, 搜索阈值M等；

7) 根据目标函数计算个体适应度值, 记录最佳适应度bF和最差适应度wF, 根据式(7)进行位置更新；

8) 根据折射反向学习原理, 对最优解进行折射操作, 判断反向解是否优于最优解, 若是则进行替换, 反之不变；

9) 判断迭代次数是否为M正整数倍, 是则按照式(14)～式(16)进行扰动和替换, 否则跳过此步骤, 进入下—步；

10) 判断是否满足停止迭代条件, 若满足则停止迭代, 并输出当前最优解, 否则返回步骤7)。

4 算例分析

为验证所提出的配电网重构算法的有效性, 使用IEEE 33节点和118节点两个配电系统算例。IEEE33系统中存在节点33个、 支路37条, 其中联络开关支路5个； 系统的基准电压为12.66 kV, 有功功率为3.715 MW, 总负荷为3 715+j2 300 kVA； IEEE118系统中存在节点118个, 支路132条, 其中联络开关支路15条, 系统基准电压为12.66 kV, 负荷为22 709.+j1 704 1 kVA。假定平衡节点的电压标幺值为1。使用Matlab R2018a编写程序, 计算环境为： Intel(R) Core(TM)i3-2120 CPU @3.30 GHz的处理器, 4 GByte的内存。算法参数设置如下：N=30,Tmax=50次,D=3,M=15,z=0.03,p=25, 重构结果如表1所示。

表1 重构结果对比

经过多次迭代, 比较重构前后的线路损耗与节点电压可知, 采用本算法进行配电网络重构后得到如下结果：

1) IEEE33节点系统中, 网络的有功损耗由202.68 kW降低至140.24 kW, 相比于初始拓扑减少了30.4%；

2) IEEE118节点系统中, 网络的有功损耗由1 294.30 kW降低至805.9 kW, 相比于初始拓扑减少了37.7%。

图2、 图3给出了两个系统重构前后各支路有功损耗的对比图, 可以证明本方法对降低网络损耗方面有较好表现。对比两个系统的重构结果, 可以看出所提出的策略在118节点这个较为复杂的拓扑结构的条件下表现更优, 进一步说明本方法在复杂网络拓扑优化方面的有效性。

图2 IEEE33系统重构前后线路图有功损耗对比 图3 IEEE118系统重构前后各线路有功损耗对比Fig.2 IEEE33 nodes system comparison of line active power loss before and after Fig.3 IEEE118 nodes system comparison of line active power loss before and after

图4、 图5给出了重构前后各节点电压的对比图, 虽然没有将电压偏差作为目标函数, 但从图4、 图5中可以看出, 网络重构后的拓扑结构与初始网络拓扑相比具有更均衡的电压分布, 尤其是118节点系统中电压分布更均衡。同时可以看出, 在IEEE33系统中, 最低点电压由0.871 3 p.u.提升到0.940 1 p.u., 在IEEE118节点系统中, 最低点电压由0.911 8 p.u.提升到0.969 2 p.u., 电压质量明显提高。

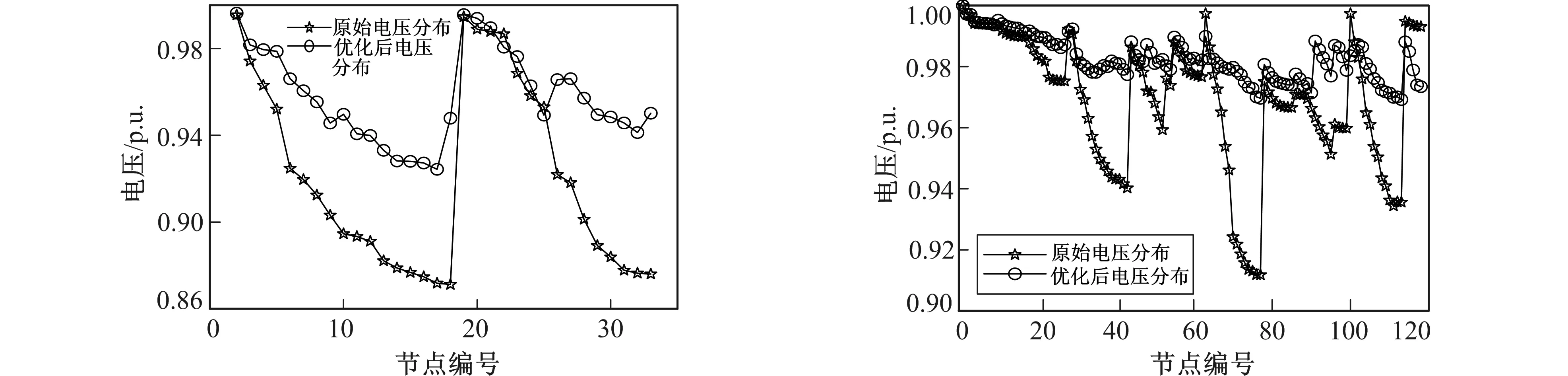
图4 IEEE33系统重构前后各节点电压比较曲线图 图5 IEEE118系统重构前后各节点电压比较曲线图 Fig.4 IEEE33 nodes system voltage comparison before and after reconfiguration Fig.5 IEEE118 nodes system voltage comparison before and after reconfiguration

图6 算法进化特性Fig.6 Algorithm evolution characteristic

将提出的改进黏菌算法分别与标准黏菌算法和粒子群算法进行比较, 多次运行平均结果如图6所示。由图6可以看出, 本算法平均迭代7次左右可达到最优解, 而标准黏菌算法和粒子群算法分别平均迭代11次左右和15次左右才可求得最优解, 验证了改进黏菌算法有较快的收敛速度, 能有效均衡全局和局部搜索能力。

综上, 笔者提出的基于改进黏菌算法的配网重构方法在IEEE33和118节点系统中运行, 在减小网损、 电压平衡和迭代次数上都表现出良好的效果, 证明了本方法在配网重构应用中的有效性。

5 结 论

1) 笔者以减少网损和负荷均衡两个目标建立了配电网重构模型, 采用随机权重, 将两个目标函数做归一化处理, 经过算例分析验证了本算法在改善网损、 维持负荷均衡和提升电压质量等方面均有良好表现。

2) 针对标准黏菌算法中出现的收敛速度差、 易获得局部最优解等问题, 设置搜索阈值和高斯扰动, 有效提高了收敛速度, 引入折射反向学习策略跳出局部最优解, 更好地平衡全局和局部搜索能力。

3) 为解决复杂拓扑结构在重构中出现大量不可行解的问题, 笔者将Prim算法与连续支路交换算法相结合对网络拓扑进行优化, 全面覆盖可行解。算例分析验证了本算法在复杂网络中有更优表现, 进一步证明本算法的有效性和可行性。