基于VMD-分形理论的短期电力负荷预测
2022-12-10徐建军王硕昌
徐建军, 王硕昌
(东北石油大学 电气信息工程学院, 黑龙江 大庆 163318)
0 引 言
分形理论可有效处理许多复杂的非线性模型, 并且对比其他传统模型, 例如灰色预测模型、 ARIMA(Autoregressive Integrated Moving Average)模型、 BP(Back Propagation)神经网络模型、 模糊预测模型、 插值预测模型、 回归预测模型等, 其不需要训练, 也不存在结果不收敛的现象。李昂儒等[1]利用分形插值函数获取相邻样本的局部信息, 再使用多个评价指标维度对预测效果进行估计。关学忠等[2]通过经验模态分解(EMD: Empirical Mode Decomposition)对原始分解, 再通过分形插值函数分别进行预测, 最后将预测结果同BP神经网络模型进行对比, 证明了EMD-分形预测模型的预测精度更高。肖瑶[3]提出了一种应用于离散电力采样数据的分形特征值计算方法, 并且通过对盒维数逆运算实现了对负荷的预测。赵飞[4]通过计算电力系统短期负荷的分维数和Kolmogorov熵, 证明了相同空间状态下的电力系统负荷具有分形的特征, 并且通过线性回归方法进行局部拟合预测未来几天内电力系统负荷。高金兰等[5-6]设计了一种基于VMD-IWOA-LSSVM(Variational Mode Decomposition-Improved Whale Optimization Algorithm-Least Square Supprt Vector Machine)的短期负荷预测模型, 通过变分模态分解对原始负荷数据进行分解, 再输入到通过鲸鱼算法优化后的最小二乘支持向量机模型中, 提高了负荷预测的精度。
分形函数系统是以分形理论为基础, 通过映射函数寻求吸引子曲线达到预测的目的。李小燕[7]通过分形插值函数选取相似日对实测日进行气象预测, 在选取参考日的数据对实测日的预测数据进行回归, 进一步提高了预测精度。李萌[8]通过设置调整参数和不断更新迭代初始点对分形插值函数进行修正, 使其能对中长期电力负荷进行预测。关学忠等[9]利用分型理论中的拼贴定理和分形插值函数对各个分解序列进行合理预测。李如琦等[10]通过灰色关联法选取相似日的数据, 通过数据的特点对数据进行分段, 在利用分形插值函数对分段数据进行预测和拟合。刘映等[11]通过改进垂直因子的分形插值函数对样本数据进行小波分析, 通过小波分析确定分形插值点, 这种分析方法有效提高了预测精度。目前所有的根据分形理论预测负荷的方法都存在分形曲线复杂、 噪音数据过多、 拟合过度的问题。为解决上述问题, 笔者建立了一种基于VMD(Variational Mode Decomposition)-分形理论的短期电力负荷预测模型, 通过对原始负荷序列进行分解, 降低噪声序列的影响, 使分形预测曲线更为平滑, 预测结果准确性更高。
1 分形插值函数定理
分形插值函数是通过其本身数据所含有的规律进行插值[12], 生成迭代函数系统(IFS: Iterative Function System),该系统满足压缩映射定理和拼贴定理[13]。
对一个给定的数据集{(xi,yi)∈R2,i=0,1,2,…,N}, 其在R2内有以下的放射变换IFS{R2:ωi,i=1,2,…,N},ωi是下式的仿射变换。
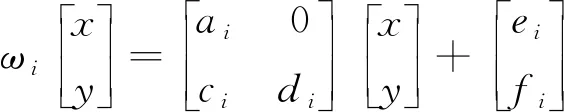
(1)
其中ai、ci、ei、fi为待求参数,di为自由参数, 通常表示插值曲面的光滑程度。则放射变换的函数端点必须满足

(2)
迭代函数系统IFS通过仿射变换生成的分形插值函数(FIS: Fractal Interpolation System)端点条件经过整理后可得

(3)

2 模型建立
笔者提出了一种新的预测模型, 该模型通过变分模态分解(VMD)对基准日的负荷数据进行分解, 分解成趋势项、 扰动项(IMF1)、 噪音项(IMF2,IMF3,IMF4)。通过对趋势项和扰动项的数据曲线进行重标极差法分析, 确定是否具有分形的特征。通过趋势项和扰动项的曲线特征计算垂直尺度因子, 建立迭代函数系统(IFS: Iterative Function System)分别对趋势项、 扰动项(IMF1)、 噪音项(IMF2,IMF3,IMF4)进行迭代计算, 再相加, 最终得到预测结果。笔者选取美国大西洋电力公司(Atlantic Electric Power Company)提供的负荷数据。
VMD-分形理论的算法实现过程如图1所示。
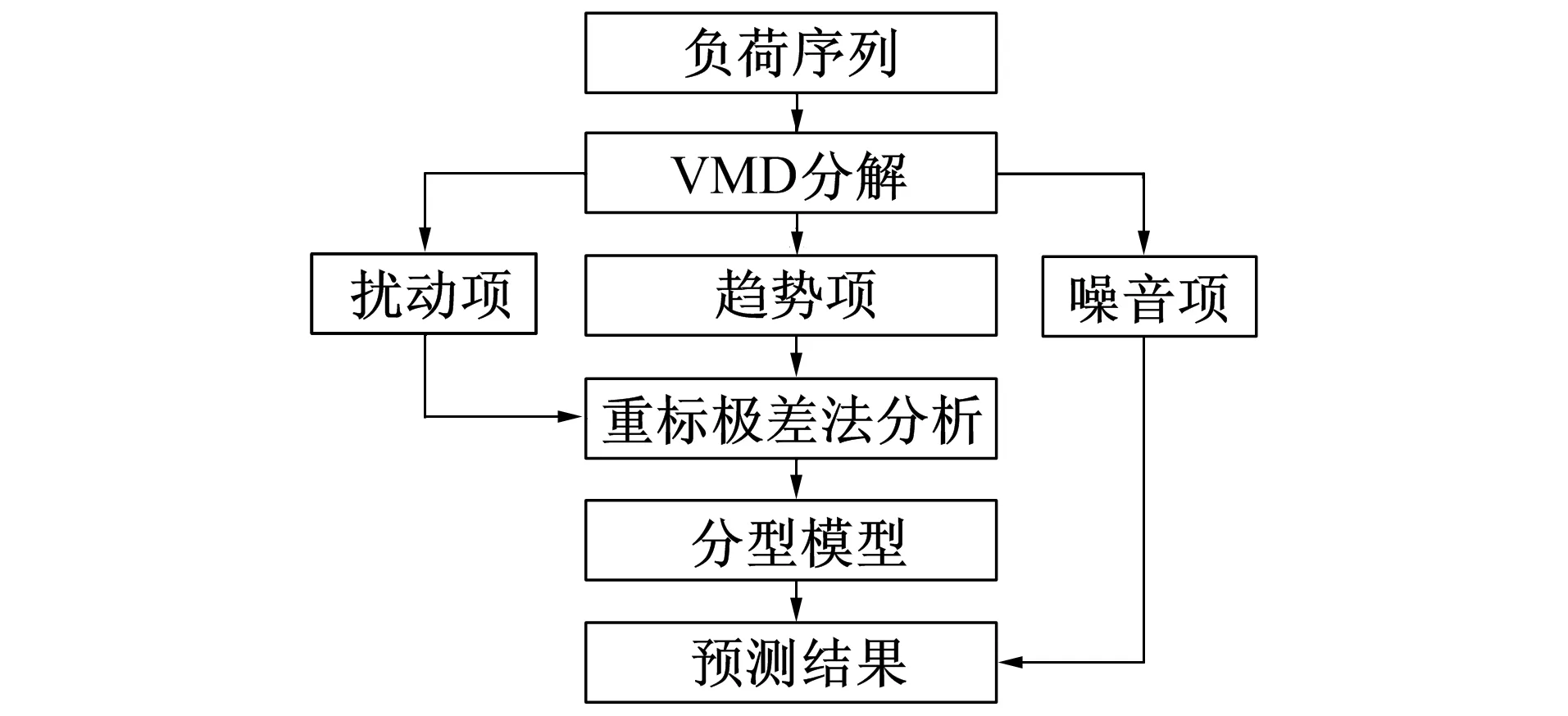
图1 基于VMD-分形理论短期负荷预测模型Fig.1 Short-term load forecasting model based on VMD-fractal theory
VMD的目的是将原始复杂的电力负荷信号曲线分解为K个调幅调频子信号, 通过维纳滤波去噪, 初始化有限带宽参数α和中心角频率, 获得K个估计的中心角频率ωK, 利用交替方向乘子法更新各模态参数以及中心频率, 并将各个模态解调到相应基频带, 最终达到各个模态估计带宽之和最小的目的[14-15]。
原始负荷序列分解过程如下。
1) 对每个模态函数uk(t), 采用Hilbert进行变换计算相应的解析信号, 其单侧频谱如下
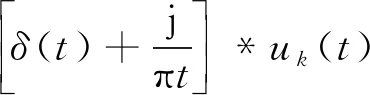
(4)
其中*为卷积运算符,δ(t)为狄拉克函数, {uk},{ωk}分别为对应的第k个子信号对应的模态分量和中心频率。
2) 模态函数uk(t)和所对应的中心频率ωk的指数项e-jωkt混叠, 将频谱调整到要对应的基频带频谱

(5)
3) 由强调信号的高斯平滑法估计带宽, 求解约束函数条件的变分函数

(6)
其中f为原始信号, {uk}={u1,…,uk}, {ωk}={ω1,…,ωk}。
4) 采用二次惩罚因子α和拉格朗日算子λ(t),表达式如下

(7)
5) 采用交替算子法解决上述问题, 二次优化问题的解为
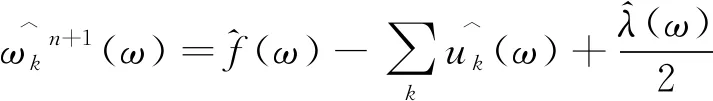
(8)
6) 同上述过程, 中心频率的更新公式为
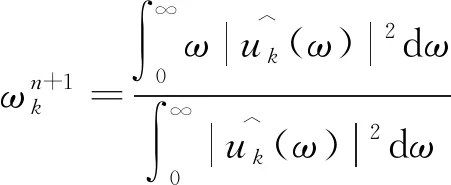
(9)

将2021年9月3日作为基准日进行电力负荷的VMD分解, 如图2所示。
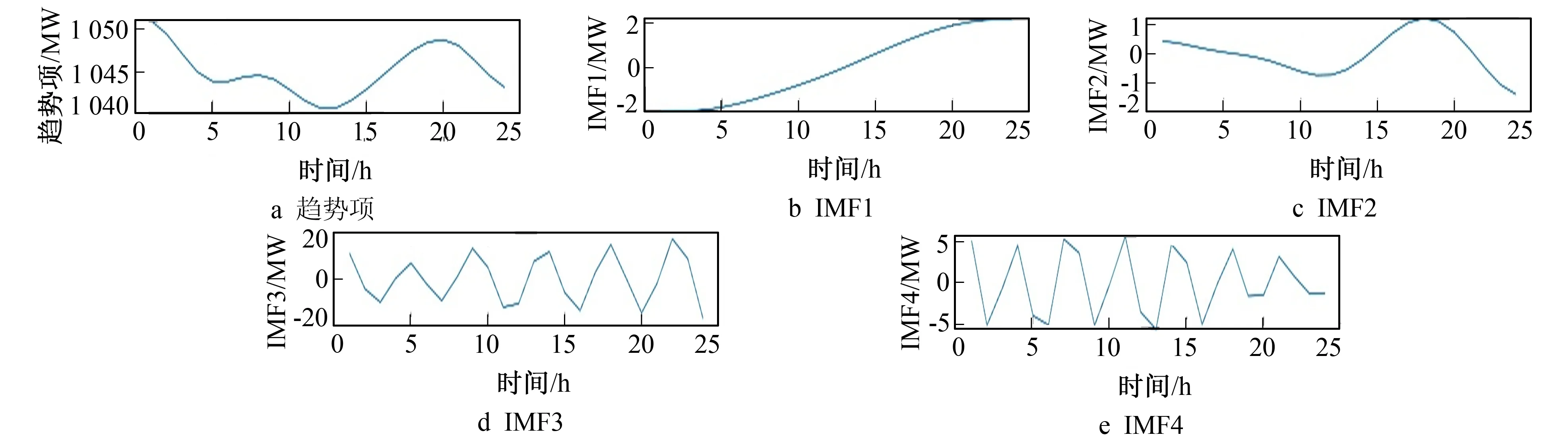
图2 VMD负荷分解结果Fig.2 The result of VMD load sequence decomposition
为减少分形迭代函数的波动性, 增加负荷预测的精度, 要对各个模态量进行判断其是否具有迭代的价值。由图2可知, 趋势项和扰动项(IMF1)不具备周期性特征而且上下波动幅值很大, 具有整体的特征且周期性特征不明显。所以采用分形迭代的方式对趋势项和扰动项(IMF1)进行进一步的预测, 而噪声项(IMF2、IMF3、IMF4)具有明显的周期性特征且幅值较小, 预期迭代效果不好, 所以作为噪声序列和趋势项和扰动项预测的结果相加。对趋势项和扰动项进行重标极差法检验, 验证是否有分形的特征。
重标极差法是对时间序列的预测性进行分析, 其一般步骤如下。
对时间序列{xt,t=0,1,2,…,N}, 设EN为时间序列的均值,X(t,N)为该序列的累积离差,R(N)为该序列的极差,S(N)为标准差, 则有

(10)
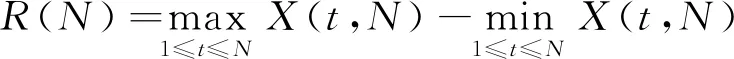
(11)

(12)
则R(N)/S(N)为重标极差, 即为
(R/S)N=cNH
(13)
其中H为Hurst指数,c为正常数, 与参数N无关。时间序列中的Hurst指数H和分形维数D满足:H+D=2。
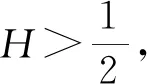
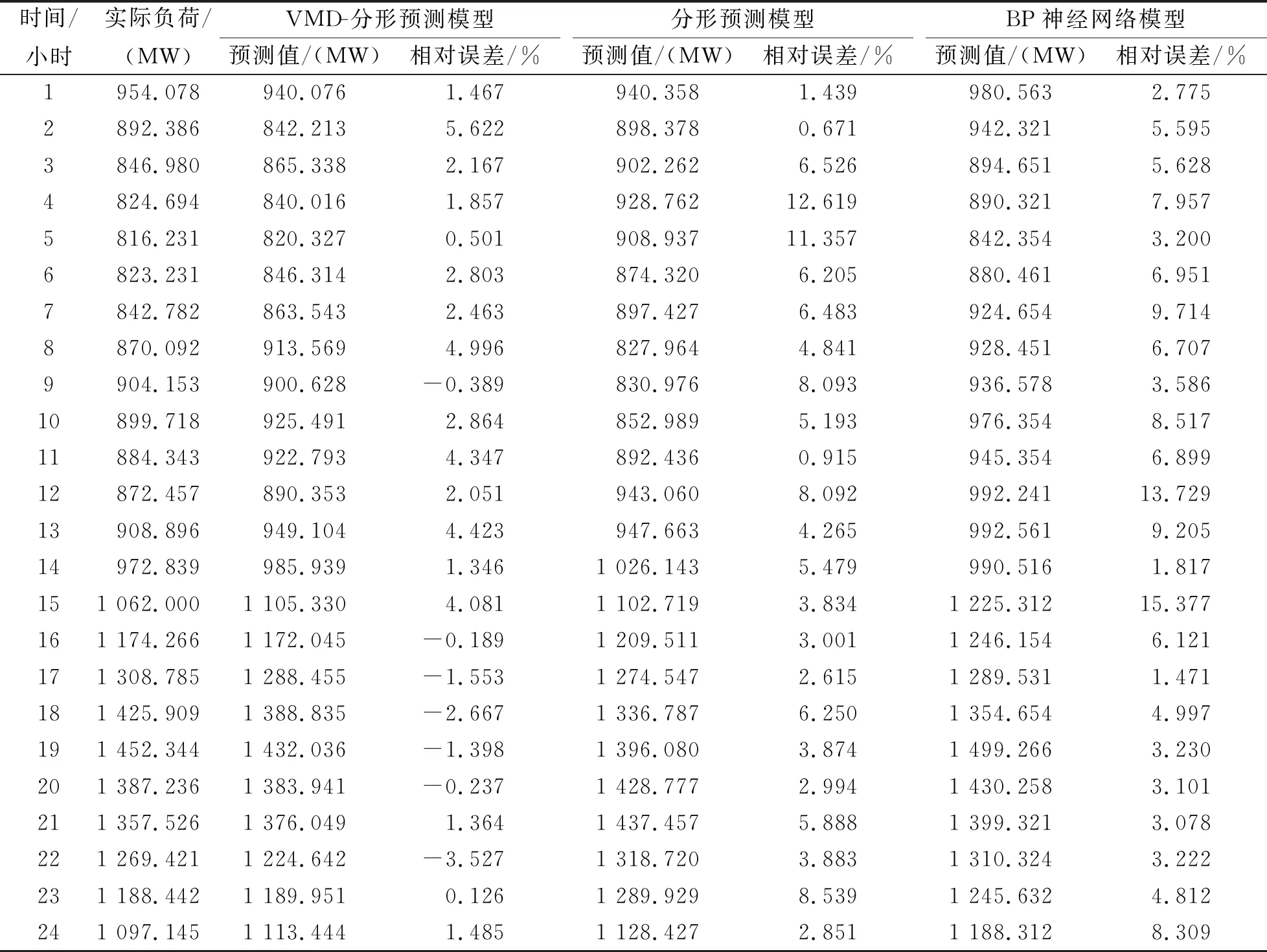
图3、 图4中的曲线斜率分别代表了趋势项的Hurst指数和扰动项的Hurst指数。趋势项的Hurst指数为0.923 416, 扰动项(IMF1)的Hurst指数为0.934 246, 0.5 图3 趋势项的R/S分析 图4 扰动项的R/S分析 Fig.3 R/S analysis of trend term Fig.4 R/S analysis of disturbance term 通过研究趋势项和扰动项(IMF1)曲线特征, 取趋势项曲线导数为0的点作为插值点, 扰动项(IMF1)的插值点和趋势项相互对应。笔者借鉴了文献[16]和文献[17]的方法, 根据趋势项和扰动项(IMF1)的插值区间计算出压缩尺度因子, 计算方法如下。 1) 将趋势项和扰动项(IMF1)根据曲线波动趋势找到极值点, 将极值点作为插值点并且划分插值区间。 2) 将所有插值区间所在序列的第1个数据和最后序列的最后一个数据, 组成一个数据量为N+1的插值点集。 3) 通过每个插值区间的第1个点和最后一个点做一条直线, 令d为插值区间序列中剩余点到直线距离的最大值。 4) 对每个插值区间所在序列都进行上述操作, 得到的集合为{ui}。通过 (14) 计算垂直尺度因子。 5) 求出每个插值区间所在序列的dq, 垂直压缩因子就是所有dq的算术平均值。通过上述步骤求得压缩尺度因子分别为0.68和0.73。建立迭代函数系统(IFS), 如图5、 图6所示。 图5 趋势项预测数据曲线 图6 扰动项(IMF1)预测数据曲线 Fig.5 Trend item forecast data curve prediction data curve Fig.6 Perturbation(IMF1) term 图7是VMD-分形预测模型、 分形预测模型、 BP神经网络预测模型[18-19]的对比图。通过图7可清晰地看到VMD-分形预测模型比分形预测模型和BP神经网络模型的预测效果好。表1是2021年9月4日的预测结果, 从表1中可以看出VMD-分形预测模型的相对误差较分形预测模型和BP神经网络预测模型的相对误差小。其中经过计算VMD-分形预测模型的MAPE(Mean Absolute Percentage Error)为2.244 55%, 分形预测模型的MAPE为5.246 5%, BP神经网络预测模型的MAPE为6.083 7。VMD-分形预测模型的MAPE比分形预测模型和BP神经网络预测模型降低了5%左右, 证明了VMD-分形预测模型比分形预测模型和BP神经网络预测模型的预测效果更好。 图7 3种预测模型和实际值的比较Fig.7 Comparison of three prediction models and actual values 表1 3种模型预测值 笔者针对传统的分形预测模型进行改进, 通过变分模态分解对复杂的负荷数据处理, 并且加入了根据插值区间计算尺度因子的方法, 提出了一种新的VMD-分形预测模型。通过与传统分形预测模型和BP神经网络预测模型进行对比, 结果表明VMD-分形预测模型预测精度更高, 预测曲线更贴合实际负荷曲线。综上所述, VMD-分形预测模型在短期电力负荷预测中较传统分形预测模型和BP神经网络预测模型更具有优势。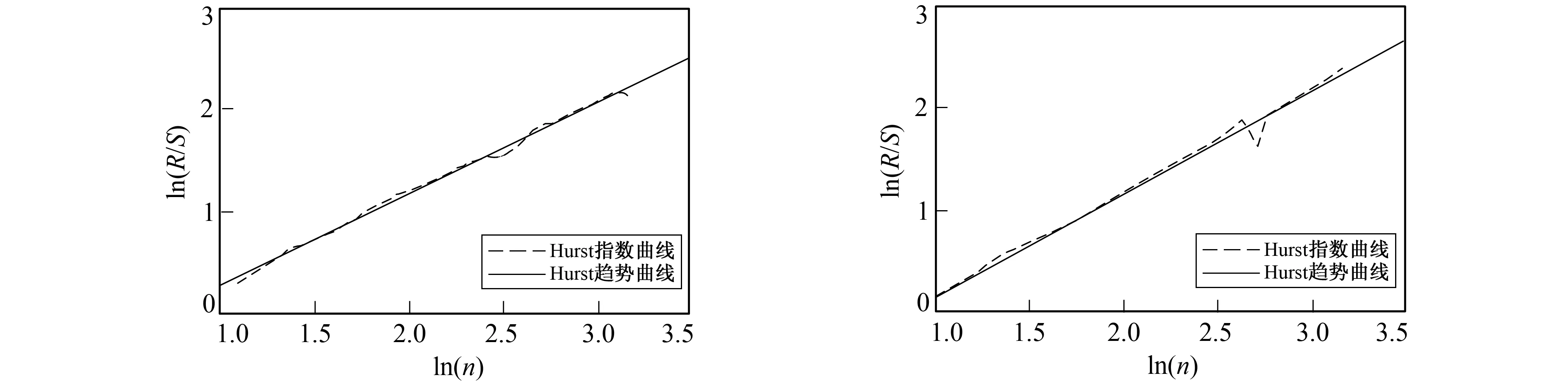
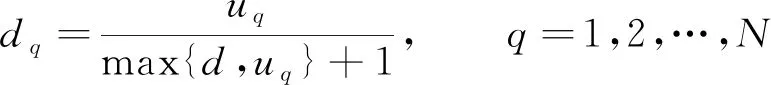

3 实验结果

4 结 语
