针对密码芯片电磁辐射泄漏的特征选择方法
2022-12-10郭剑虹
文 毅 郭 澍 孔 昊 郭剑虹
(国家应用软件产品质量检验检测中心(北京软件产品质量检测检验中心) 北京 100193) (wenyi.tc@kw.beijing.gov.cn)
芯片在执行密码运算过程中,通常会泄漏功耗、电磁辐射和执行时间等侧信道信息,攻击者通过采集和分析侧信道信息往往能够获取芯片内部的敏感数据,严重威胁到密码芯片的安全.1996年,Kocher[1]提出时间攻击,利用泄漏的执行时间成功获取了RSA算法的密钥.1999年,Kocher等人[2]提出简单功耗分析和差分功耗分析,利用泄漏的功耗实现了对DES算法的攻击.随后,相关研究人员相继提出电磁分析[3-5]、模板攻击[6]、相关功耗分析[7]和互信息分析[8]等侧信道攻击.随着新型攻击方法的不断出现,密码芯片的安全性也遭遇了前所未有的巨大挑战.在上述方法中,电磁分析和功耗分析一般需要减小或消除电磁泄漏迹或功耗迹中的噪声,通过提高信噪比减少分析所需的电磁泄漏迹或功耗迹数量.而模板攻击则是对噪声进行精确建模,以获取电磁泄漏迹或功耗迹上更多的可利用泄漏信息.因此,到目前为止,模板攻击被认为是最有效的侧信道攻击方法.
模板攻击包含模板构建和模板匹配2个阶段.实际上,在对芯片的电磁泄漏迹或功耗迹构建模板时,为了获取更多的泄漏信息频率分量,通常会使用很高的采样率对电磁泄漏迹或功耗迹的振幅进行采样,以至于每条电磁泄漏迹或功耗迹中包含大量的采样点,进而占用分析设备过多的计算资源和使用内存.所以,在构建模板前,一般需要对采集的电磁泄漏迹或功耗迹进行降维处理,选出包含所执行特定指令序列最多信息的点作为特征点,然后再以特征点构建模板,从而提高模板构建精度和攻击效率.目前,基于机器学习和深度学习的模板攻击成为侧信道攻击的研究热点,关于模板攻击的特征选择方法研究早已成熟,最新相关研究[9]成果较少.
2002年,Chari等人[6]建议对每个子密钥对应的功耗迹计算平均值,从平均功耗迹上选择差异最大的点作为特征点;2004年,Rechberger等人[10]建议计算平均功耗迹的成对差异之和,将差异最大的点选为特征点;2005年,Agrawal等人[11]建议采用差分功耗分析方法,将差分功耗曲线上尖峰最明显的点作为特征点;2006年,Gierlichs等人[12]建议采用平均功耗迹的成对差异平方和进行特征选择,并提出基于T-检验的特征选择方法;同年,Archambeau等人[13]建议采用主成分分析方法进行特征选择,通过对功耗迹提取主成分、抛弃次要成分实现功耗迹降维;2008年,Standaert等人[14]提出基于Fisher线性判别分析的特征选择方法,实现了对功耗迹的降维处理;2010年,Elaabid等人[15]建议采用相关系数方法,将功耗迹中与子密钥具有较大相关性的点选为特征点,后来该方法在模板攻击中得到了广泛应用[16-17].
虽然上述方法都能够从功耗迹上有效选出特征点,但通常需要消耗大量的功耗迹数量和计算资源,导致模板构建成本较高.为此,本文提出基于汉明重量模型的特征选择方法,通过对比相关系数特征选择方法,本文方法能够同时减少电磁泄漏迹或功耗迹数量以及计算资源消耗,极大降低了模板构建成本.
1 电磁泄漏迹的统计方法
芯片的电磁分析或功耗分析[18]利用了一个事实,即电磁辐射或功耗依赖于芯片执行的操作和处理的数据.电磁辐射迹通常由近场探头对芯片表面的电磁辐射信号进行测量,再经数字示波器采样后得到电压值向量,其电压值正比于电磁辐射能量.电磁泄漏迹或功耗迹的统计特征可分为单点特征和多点特征.单点特征主要关注某个固定时刻的电磁辐射泄漏,而多点特征则关注电磁泄漏迹中2个点或多个点之间的相互关系.对于多条电磁泄漏迹或功耗迹之间的相似性与差异性,可使用统计分析进行度量.
1.1 电磁泄漏迹的统计特征
当芯片对恒定数据执行相同的指令序列时,电磁泄漏迹上单个点的泄漏值近似服从高斯分布,其概率密度函数可由均值和标准差2个参数进行定义:
(1)

(2)
(3)
单点特征不能刻画多个点之间的相关性,为考虑2个点或多个点之间的相关性,需采用多元高斯分布对电磁泄漏迹建模,其概率密度函数为
(4)
多元高斯分布可由均值向量m和协方差矩阵C定义,其中m包含了电磁泄漏迹中所有点的均值,即mi=E(xi),C包含了电磁泄漏迹中点i和点j之间的协方差,即cij=Cov(Xi,Xj).
在模板攻击中,将(m,C)定义为模板.但为了避免C求逆时遇到数值问题,一般使用单位矩阵取代C,即忽略各点之间的协方差,最终只由均值向量m构建简化模板.
1.2 电磁泄漏迹的统计分析
在多元统计分析[19]中,可使用距离对聚类分析和判别分析进行推导,距离反映了差异性.
假设有n条电磁泄漏迹,每条迹上有p个采样点,记ta=[ta1,ta2,…,tap]T与tb=[tb1,tb2,…,tbp]T分别为第a条与第b条迹,其中a,b=1,2,…,n.则第a条与第b条电磁泄漏迹之间的明氏距离为
(5)
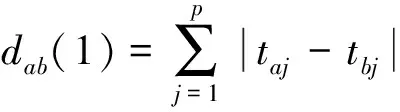
假设存在2个类别G1和G2,分别从G1,G2中抽取n1,n2条电磁泄漏迹,且每条迹上有p个采样点.对于未知类别的迹t=[t1,t2,…,tp]T,可使用欧氏距离对t进行判别分类.
首先,计算t与G1,G2之间的欧氏距离:
(6)
(7)
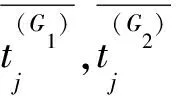
然后,按距离最近原则对t进行判别分类:
当D(t,G1)<D(t,G2)时,t∈G1;
当D(t,G1)>D(t,G2)时,t∈G2;
当D(t,G1)=D(t,G2)时,t待判别.
当推广至多个类别时,首先计算t与每个类别的欧氏距离,然后将欧氏距离进行比较,最后将t判别到欧氏距离最小的类别中.
2 模板攻击
模板攻击通常假设攻击者拥有一个能够完全控制的样本芯片或设备,并且样本芯片与被攻击芯片的类型完全相同.攻击者首先采用多元高斯分布对样本芯片执行特定指令序列时的电磁泄漏迹进行模板构建;然后利用样本芯片的电磁泄漏模板与被攻击芯片的电磁泄漏迹进行匹配,匹配程度最高的模板将揭示出被攻击芯片的密钥.
为了提高模板构建精度以及模板匹配效率,攻击者通常需要在模板(m,C)构建前对电磁泄漏迹进行降维处理,即采用特征点构建模板,特征点反映了芯片执行特定指令序列时电磁辐射泄漏最相关的点.为了避免协方差矩阵C求逆时遇到数值问题,可采用仅由均值向量m构成的简化模板.为了验证本文提出的基于汉明重量模型特征选择方法,有必要对每个特征点单独构建简化模板.
2.1 模板构建
对于SM4分组密码算法[20]的侧信道攻击,攻击者可选择S盒输出作为中间值,每个S盒对应了8比特输入和8比特输出.假设样本芯片与被攻击芯片分别执行SM4加密运算的密钥(十六进制)为keyA=FEDCBA98765432100123456789ABCDEF,keyB=0123456789ABCDEFFEDCBA9876543210.对于攻击者而言,样本芯片的密钥keyA是已知的,被攻击芯片的密钥keyB是未知的.

(8)
2.1.1 基于汉明重量模型的特征选择方法
基于汉明重量模型进行特征选择的假设:在芯片执行相同的密码运算指令过程中,其电磁辐射泄漏依赖于内部所处理数据的汉明重量,并且汉明重量取值相同的数据会产生几乎相同的电磁辐射泄漏,汉明重量取值不同的数据会产生明显差异的电磁辐射泄漏.
基于上述假设,当芯片输入9组明文分别执行S盒相关指令进行数据运算时,被处理的9种汉明重量数据必将导致电磁泄漏迹上所对应运算时刻产生明显差异,其9个类别对应的平均电磁泄漏迹也必然存在明显差异,表现为9个类别中任意2个类别的平均电磁泄漏迹之差不为0.
对于汉明重量取值为q的类别,其平均电磁泄漏迹如式(8)所示,计算汉明重量取值分别为q1,q2的类别所对应的平均电磁泄漏迹之差,得到1组差值向量为
(9)
其中q1,q2=0,1,…,8且q1<q2,将差值向量表示为差值矩阵:
(10)
由9个不同类别得到36组差值向量,每组差值向量有p个点,使用差值矩阵T表示为36行p列,每行对应1组差值向量,每列对应电磁泄漏迹上1个采样点.
基于汉明重量模型的特征选择方法:需定义3个变量vthreshold,npositive,nnegative.变量vthreshold表示电压阈值,单位为mV,且vthreshold≥0;变量npositive表示在矩阵T的1个列向量中,元素值大于+vthreshold设定值的元素个数;变量nnegative表示在矩阵T的1个列向量中,元素值小于-vthreshold设定值的元素个数.由定义可知,npositive=0,1,…,36,nnegative=0,1,…,36.
由变量npositive和vthreshold进行特征选择,具体操作步骤为:
第1步.变量初始化.设定变量npositive的初始值为36、变量vthreshold的初始值为0 mV.
第2步.特征点初选.对于矩阵T的每个列向量,统计该列向量中元素值大于+vthreshold值的元素个数,如果某一列向量经统计后得到的元素个数等于npositive值,则将该列向量的列索引号作为特征点的索引.
第3步.特征点复选.情形1.如果第2步操作得到的特征点数量过多,则返回第1步,保持变量npositive值不变,适当增大变量vthreshold值,重新执行第2步操作,将平均电磁辐射泄漏迹差异更大的点选为特征点.情形2.如果第2步操作没有得到任何一个特征点,则返回第1步,将变量npositive值减1,保持变量vthreshold值不变,重新执行第2步操作,以得到特征点.情形3.如果第2步操作已经得到数量适合的特征点,则执行第4步.
第4步.重复执行第2,3步,直至获得一定数量的特征点.
类似地,由变量nnegative和vthreshold进行特征选择,操作步骤完全相同,只需将变量npositive替换为变量nnegative,并将第2步操作修改为:对于矩阵T的每个列向量,统计该列向量中元素值小于-vthreshold值的元素个数,如果某一列向量经统计后得到的元素个数等于nnegative值,则将该列向量的列索引号作为特征点的索引.
将上述基于汉明重量模型选出的特征点用于模板构建,为了验证特征点的有效性,模板中只包含1个特征点j,依据式(8),对于汉明重量为q的类别,其简化模板为
(11)
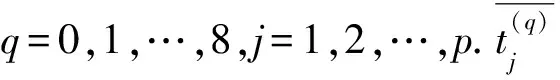
综上所述,基于汉明重量模型进行特征选择和模板构建,仅需9e条电磁泄漏迹,即样本芯片只需进行9e次SM4加密运算,其中9表示9个汉明重量类别对应的9个简化模板,e表示每个简化模板需要e条电磁泄漏迹.基于汉明重量模型的特征选择方法不存在复杂运算,计算资源需求较小.
2.1.2 基于相关系数的特征选择方法
首先对样本芯片执行e0次随机明文SM4加密运算,保存对应的明文和电磁泄漏迹,假设电磁泄漏迹上有p个点,记tj=(t1,j,t2,j,…,te0,j)T为e0条电磁泄漏迹在第j点处的值.然后根据8比特密钥空间k=(k0,k1,…,k255)T计算S盒输出的假设值,再将假设值使用汉明重量模型映射为假设电磁泄漏值,记hi=(h1,i,h2,i,…,he0,i)T为猜测密钥ki与e0组明文计算S盒输出时所映射的假设电磁泄漏值.最后,计算hi与tj之间的皮尔逊相关系数,并将相关系数值较大的点j选为特征点:
(12)
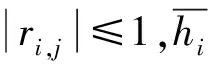
与2.1.1节类似,将上述基于相关系数选出的特征点用于模板构建,如式(11)所示.
综上所述,基于相关系数进行特征选择和模板构建,需要e0+9e条电磁泄漏迹,即样本芯片需要进行e0+9e次SM4加密运算,其中e0条电磁泄漏迹用于特征点选择,9e条电磁泄漏迹用于构建9个简化模板.基于相关系数的特征选择方法存在复杂运算,计算资源需求较大.
对比2.1.1节和2.1.2节可知,基于汉明重量模型进行模板构建时,样本芯片能够减少e0次随机明文SM4加密运算,即减少e0条电磁泄漏迹,且所需计算资源需求更小.
2.2 模板匹配
模板匹配时采用了放大模板攻击方法[17],利用S盒输出的9种汉明重量对被攻击芯片的电磁泄漏迹进行分类和匹配:
第1步.对被攻击芯片执行f次随机明文SM4加密运算,保存对应的明文、密文和电磁泄漏迹.
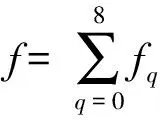

(13)

第4步.计算被攻击芯片在classq内所有fq条电磁泄漏迹的欧氏距离之和:
(14)
第5步.计算被攻击芯片所有9个类别欧氏距离之和:
(15)
第6步.对第1步中的其余255个密钥猜测值,分别执行第2~5步操作,得到对应的255个欧氏距离D.
综上所述,由于8比特密钥有256个猜测值,最终得到256个欧氏距离D.依据1.2节中的距离最近原则,将最小欧氏距离D对应的密钥猜测值作为被攻击芯片的真实密钥值.
3 实 验
为简化实验,选用同一颗芯片(STM32F103)作为样本芯片和被攻击芯片,仅以密钥keyA与keyB进行区分.在芯片执行SM4加密运算过程中,使用近场探头对芯片表面电磁辐射泄漏最明显的区域进行信号采集,然后通过数字示波器(LECROY Waverunner 8054)采样后发送至PC端保存,最后使用软件(GNU Octave)编程实现模板攻击.
实验首先对基于汉明重量模型的特征选择方法进行有效性验证,然后通过相关系数特征选择方法进行对比分析.
如图1所示,C4通道(绿色曲线)为数字示波器采集的电磁辐射信号,其中横轴对应时间,单位为μs,纵轴对应电压,单位为mV,采样率为1 GS/s,采样深度为5 kS,即变量p=5 000,时间偏移为-2 μs.C3通道(蓝色曲线)高电平区间对应SM4加密时第1轮迭代运算,大约为0~3.7 μs之间,大致对应了采样点区间(500,4 200).
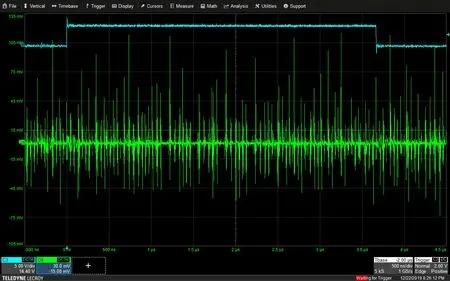
图1 示波器采集的电磁辐射信号
依据2.1节,首先对密钥为keyA的样本芯片使用9组选择明文分别执行e次SM4加密运算,同时保存对应的电磁泄漏迹, 然后使用式(8)计算9个类别的平均电磁泄漏迹.在模板构建时,通常计算e条电磁泄漏迹的均值降低噪声,实验中e=50.
3.1 基于汉明重量模型的特征点验证
3.1.1 模板构建
首先使用式(9)计算任意2个类别间的平均电磁泄漏迹之差,得到36个差值向量,通过式(10)表示为差值矩阵T,实验中T为36行5 000列.
然后依据2.1.1节操作步骤,对变量vthreshold,npositive,nnegative取值,得到基于汉明重量模型选出特征点:
当npositive=36且vthreshold=0时,得到特征点1857;当npositive=35且vthreshold=0时,未得到特征点;当npositive=34且vthreshold=0时,得到特征点1871和2220.上述操作步骤也可采用不等式进行表达,当npositive≥34且vthreshold=0时,得到特征点1857,1871,2220.
类似地,当nnegative≥35且vthreshold=0时,得到特征点217,1460,1859,1860,1869.由于点217不在有效区间内,可首先排除该点.
上述基于汉明重量模型进行特征选择,得到特征点1460,1857,1859,1860,1869,1871,2220.如果继续减小变量npositive或nnegative的值,可能会得到数量更多的特征点,也可能增加更多的无效特征点.如果增大变量vthreshold的值,将会保留平均电磁泄漏迹上差异更大的特征点,可能导致特征点数量减少.
最后使用式(11)分别为特征点1460,1857,1859,1860,1869,1871,2220构建9个简化模板.
综上可知,基于汉明重量模型进行特征选择和模板构建,样本芯片仅需9e(即450)条电磁泄漏迹.
3.1.2 模板匹配
依据2.2节,首先对密钥为keyB的被攻击芯片执行1万次随机明文SM4加密运算,同时保存对应的电磁泄漏迹.然后从1万条电磁泄漏迹中随机选择f条用于模板匹配,计算keyB第1个密钥rk0的第1个字节(256个猜测值)所对应的256个欧氏距离D.最后按照距离最近原则,找出最小D值所对应的猜测密钥,将猜测密钥与真实密钥进行比对,以判定模板匹配是否成功.重复200次随机选择f条电磁泄漏迹用于模板匹配操作,统计200次模板匹配成功率.
实验结果显示,当f=50时,特征点1460,1857,1859,1860,1869,1871,2220分别进行200次模板匹配,成功率分别为0%,63%,44%,42%,62%,85%,2%,其中特征点1871的成功率达到85%,特征点1460和2220的成功率很低.
当f=70时,特征点1871的成功率超过95%,由此可知,即便使用1个特征点构建简化模板,模板匹配也能够拥有很高的成功率.图2为f=50时,特征点1871的模板匹配成功率.
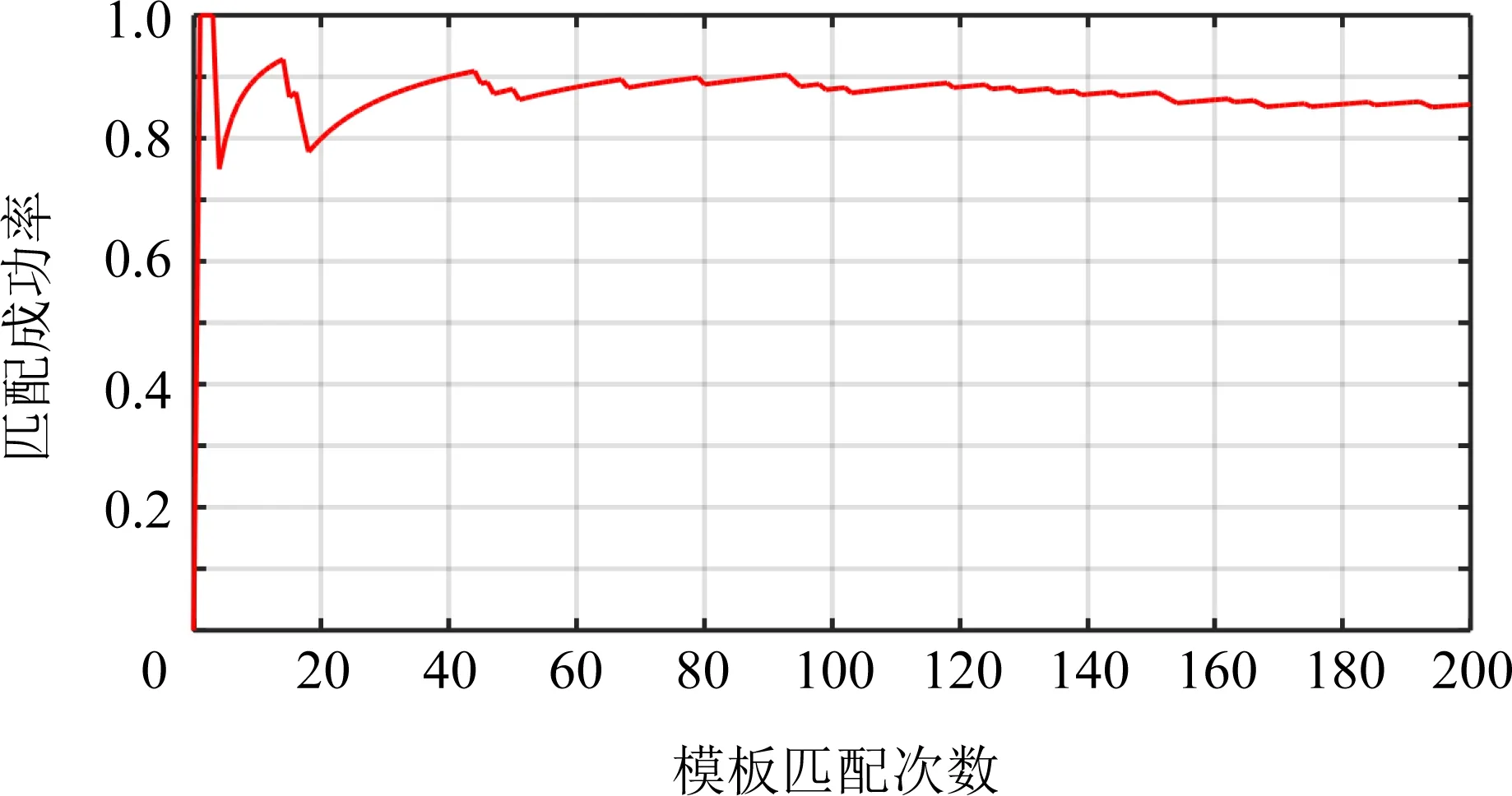
图2 特征点1871的模板匹配成功率
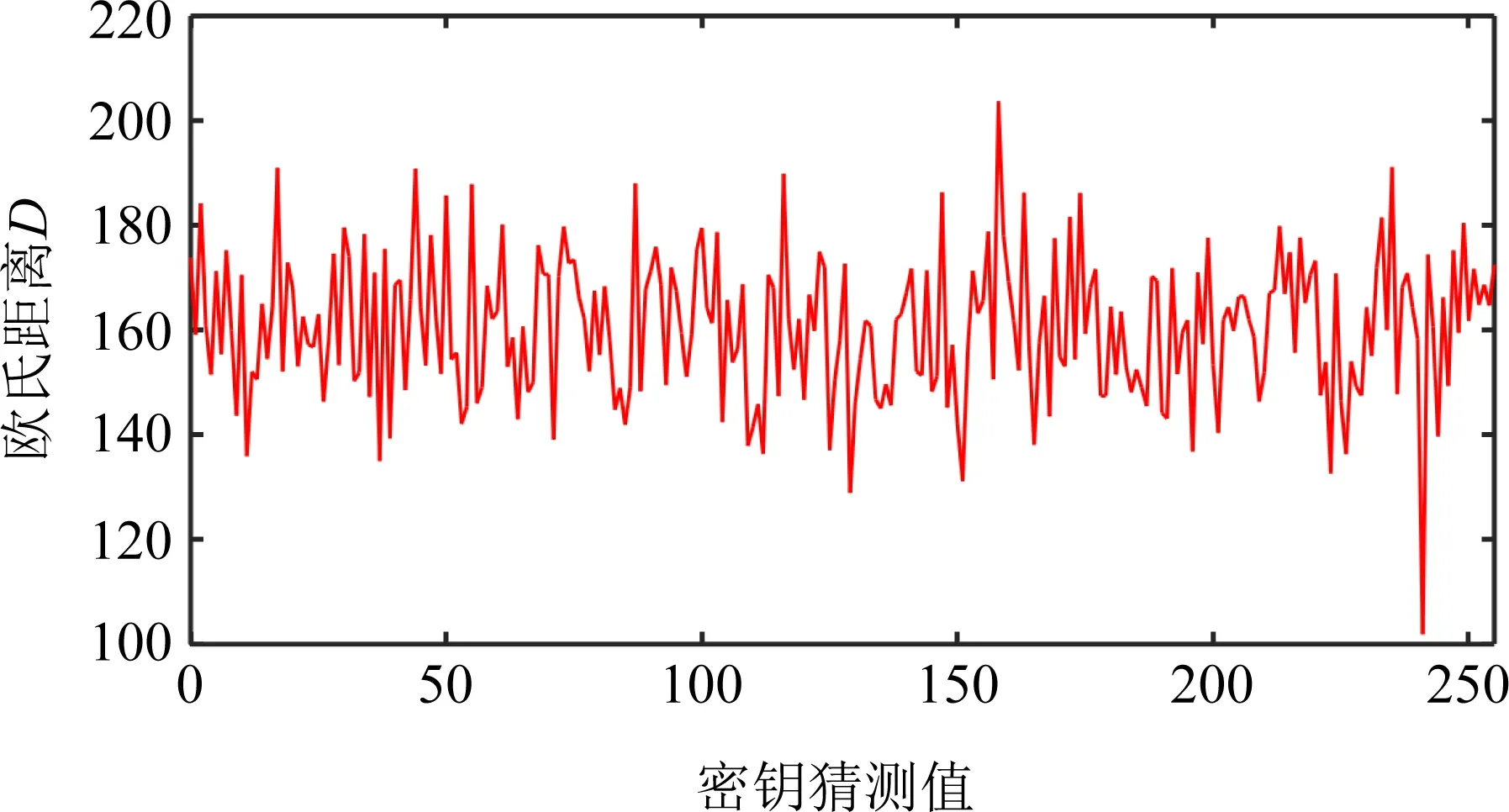
图3 特征点1871的模板攻击结果
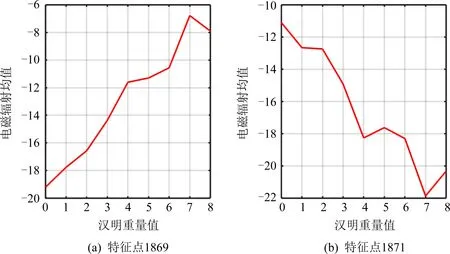
图4 特征点1871的汉明重量模板
图3为f=50时,特征点1871的模板匹配结果.如图3所示,最小的欧氏距离(数值102)对应了正确的猜测密钥(数值241),其中241(0xF1)正是子密钥rk0的第1个字节.
图4分别为特征点1869和1871的9个汉明重量简化模板.由图4可知:当汉明重量为0时,平均电磁辐射泄漏并不都是最高的;当汉明重量为8时,平均电磁辐射泄漏并不都是最低的.图4实验结果表明:芯片的电磁辐射泄漏并不是严格服从递增或递减关系.
综上实验可知,本文提出的基于汉明重量模型特征选择方法的确能够有效地选出特征点.对于模板匹配成功率较低的特征点(点1460和2220),可通过样本芯片进行有效性验证后剔除,只保留成功率较高的特征点用于模板攻击实验.
3.2 与相关系数方法的对比分析
3.2.1 模板构建
依据2.1.2节,首先对密钥为keyA的样本芯片执行e0=500次随机明文SM4加密运算,同时采集对应的电磁泄漏迹,再使用相关系数方法进行特征选择.
图5所示为假设电磁辐射泄漏与实测电磁泄漏迹之间的相关系数计算结果.当密钥猜测正确时,图5中曲线将出现明显的尖峰特性;当密钥猜测错误时,图5中曲线将表现为随机噪声,即曲线不会出现明显尖峰.基于相关系数的特征选择方法通常选取明显尖峰所在采样点作为特征点,尖峰处的点对应了较大的相关系数值.由图5选出的特征点分别为1857,1859,1860,1869,1871,1872.
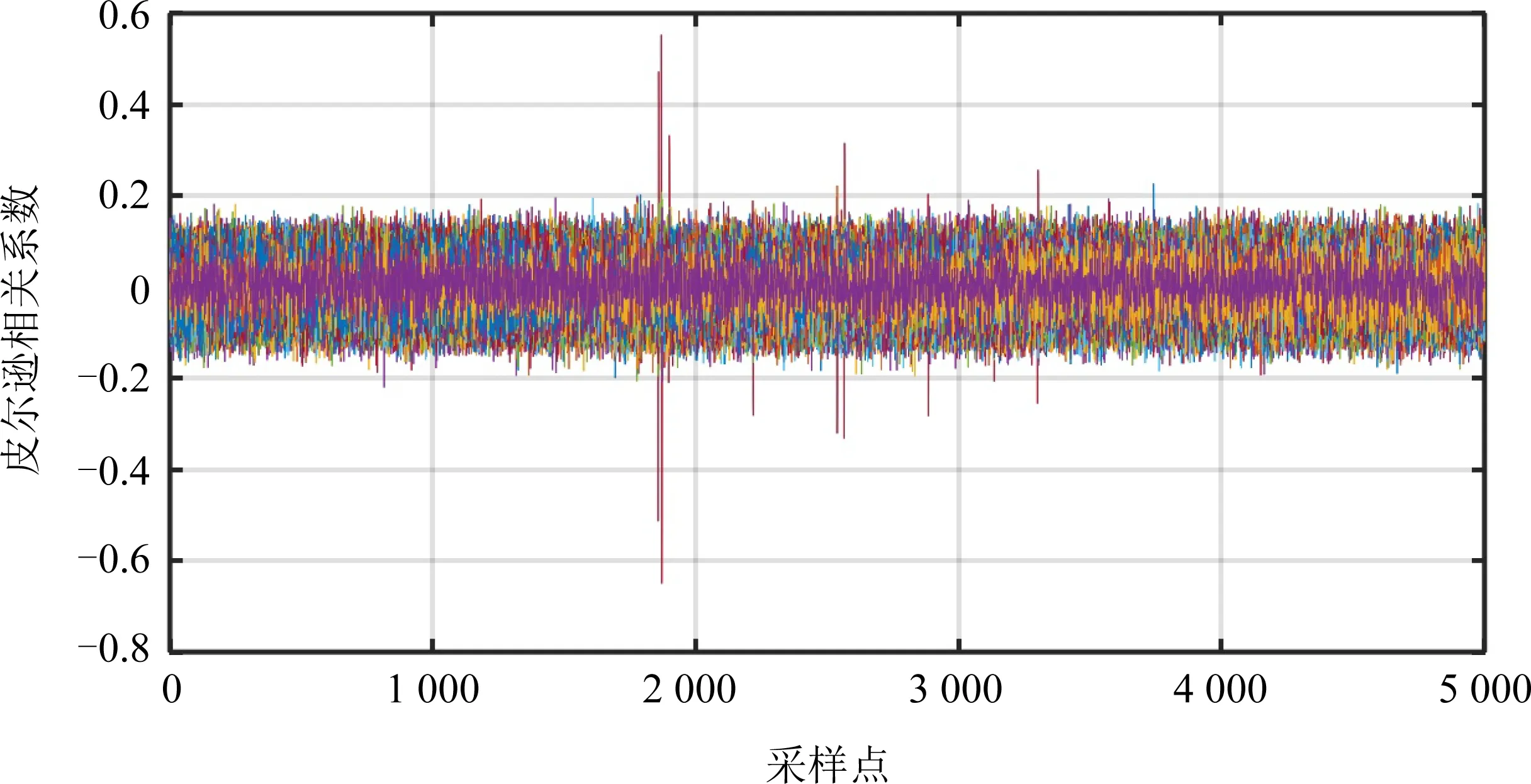
图5 基于相关系数方法的特征点选择
通过观察发现,由图5基于相关系数选出的前5个特征点与3.1.1节基于汉明重量模型选出的特征点相同,进一步验证了本文方法的有效性.在3.1.1节中,当变量npositive=32时,可得到特征点1872.
与3.1.1节类似,使用式(11)为每个特征点分别构建9个简化模板.
综上可知,基于相关系数进行特征选择和模板构建,样本芯片需要e0+9e(即950)条电磁泄漏迹,其中500条电磁泄漏迹用于特征点选择,450条电磁泄漏迹用于构建简化模板,比本文提出的基于汉明重量模型进行特征选择和模板构建多消耗e0=500条电磁泄漏迹.
3.2.2 模板匹配
依据3.1.2节,当f=50时,特征点1872的模板匹配成功率为42%,其余各特征点的模板匹配成功率与3.1.2节相同.
4 结 论
针对芯片执行密码算法过程中的电磁辐射泄漏,本文提出基于汉明重量模型的特征选择方法,通过实际攻击实验验证了方法的有效性,对比相关系数特征选择方法进行模板构建,本文方法需要的电磁泄漏迹数量更少,计算资源需求更低.通过实验,同时得出以下结论:
1) 即使使用1个特征点构建电磁辐射泄漏的简化模板,同样能够以很高的成功率恢复密钥.
2) 在有效特征点处,芯片的电磁辐射泄漏与中间值的汉明重量并不严格服从递增或递减关系,表现为汉明重量为0时电磁辐射泄漏并不都是最高的,汉明重量为8时电磁辐射泄漏并不都是最低的.
