基于可变反应器的故障电流限制器研究

2022-12-09程冠錤卢松李冬冬

浙江电力 2022年11期

谷裕，程冠錤，卢松，李冬冬

（1.中国南方电网有限责任公司超高压输电公司广州局，广州 510663；2.中国南方电网有限责任公司超高压输电公司，广州 510663）

0 引言

故障电流限制器作为输电线路的重要组成部分［1］，因其机械结构简单［2］，被广泛用于限制电网短路电流［3-4］和高次谐波［5］。

随着电力系统负荷加大，特高压输电系统［6-8］的建设迫在眉睫，但传统电抗器的安全工作电压阈值低于电力系统工作电压，致使电抗器的寿命大幅降低。此外，较高的短路电流可能会损坏变压器和发电机等电网部件。因此，需要在电网中加入FCLs（故障电流限流装置），以保证电网设备的安全稳定运行。

而故障电流限制有多种方式，包括SFCLs（基于超导电阻的故障电流限制器）［9-11］、电流短路限制器、FACTs（柔性交流输电系统）［12-14］、正温度系数［15］、ISFCLs（基于电感饱和的故障电流限制器）［16］、PEFCLs（基于电力电子的故障电流限制器）［17-20］和串联谐振限制器。

尽管这些设备实现了输电线路的有效保护，但其昂贵的造价和维护成本却给国家电力系统带来不小负担。例如，SFCLs 不仅价格昂贵，而且在一定的温度条件才能进行正常的运转；FACTs价格昂贵且复杂，对于需要大规模应用故障电流限制器的输电线路而言，ISFCLs虽然无需在特定环境下运行，但每次短路后都要更换熔断器和连接器，给工作人员的运维工作造成严重负担，而且由于其电抗固定，在正常运行条件下，会导致显著的电压下降和无功功率消耗。

因此，针对传统故障电流限制器存在的电压下降和无功功率消耗的问题，本文采用正常情况下低阻抗运行，短路后立即产生高阻抗的方式进行故障电流限制。因此，可以达到限制短路后的故障电流而在正常情况下无压降的目的，较好地解决了传统故障电流限制器的不足。

同时，随着可变反应器研究的发展，文献［21］论述了基于堆芯饱和的故障电流限制器的设计和构造。在该故障电流限制器中，通过超导绕组的大直流电流，铁芯保持在饱和状态，致使在正常网络条件下，故障电流限制器的电抗非常低。短路后，故障电流产生的磁通克服了直流磁通，导致铁芯从饱和状态放电，从而使故障电流限制器的电抗增加。然而，这种结构也存在一定的缺点：超导绕组的成本高以及其特殊的温度条件［22］。

为了实现输电线路过大短路电流的有效控制，解决传统故障电流限制造价和运维成本高的问题，本文提出了一种结构简单、价格低廉的VFCL（可变故障电流限制器）。该反应器不需要特殊的维护条件，就可以轻松回收，无需任何费用。该反应堆具有固定和移动的堆芯以及可变的气隙。当发生短路时，故障电流限制器气隙长度自动闭合，故障电流限制器电抗显著增大。同时通过遗传模块对反应器进行了优化设计和模拟。最后，采用有限元方法对VFCL 模型进行分析模拟，结果表明所提设计具有较好的性能。

1 可变反应器原理

为了在无电压降和无功功率消耗的条件下进行故障电流限制，本文以可变反应器结构作为VFCL 的总体架构。可变反应器主要由凹型固定堆芯、棒型移动铁芯和可变气隙组成，如图1 所示。其中，UCFC为凹型固定堆芯的电路电压，gCFC为空气间隙间距。

图1 可变反应器原理图

可变反应器在正常阈值电流情况下运行，气隙长度处于长距离状态，致使VFCL 的电感处于低水平状态。当可变反应器线圈感应出超阈值短路电流时，超阈值短路电流从凹型固定堆芯的线圈绕组中流过，在棒型移动铁芯和凹型固定堆芯之间因电磁作用产生吸引力，棒型移动铁芯在吸引力的作用下，向凹型固定堆芯方向移动，造成气隙闭合［23-25］，VFCL的电抗迅速增加，从而限制了故障电流。

此外，在可变气隙中加入一个弹簧，两端分别连着凹型固定堆芯和棒型移动铁芯，以便在故障清除后将其恢复到先前的位置。

同时，由于棒型移动铁芯在移动时处于高速状态，致使反应堆的磁链在移动过程中基本保持稳定。如图2所示，当凹型固定堆芯通入的电流显著增加时，电枢速度varm变大，磁链保持不变。

图2 棒型移动铁芯移动时电流和磁链的变化曲线

当磁芯移动时，绕组中会产生一种称为反电动势的运动电压。反电动势极性与网络电压相反，促使故障电流降低。因此，在线圈短路之前，系统位于a点的曲线上。当感应短路时，工作点从曲线上的a点移动到b点，电流迅速减小。当堆芯移动时，故障电流限制器充当电机，将一些电网能量转换为机械能，电流减小，如式（1）—（4）所示。

式中：UCFC为凹型固定堆芯的电路电压；RCFC为凹型固定堆芯的绕组电阻；λ为磁链；t为棒型移动铁芯的移动时间；L为凹型固定堆芯的绕组电感；i为电路电流；x为棒型移动铁芯的电枢位置；E为感应电压。

根据上述表达式得到可变反应器的等效电路，如图3所示。

图3 可变反应器等效电路

2 模型分析

2.1 基于电磁方程的故障电流限制器解析模型

前面介绍了可变反应器的原理，但要将可变反应器应用于故障电流限制器，还需要了解电抗器棒型移动铁芯和凹型固定堆芯之间的电磁力系数［26-28］，计算可变气隙中与故障电流有关的磁通量参数。本文提出了基于电磁方程的故障电流限制器解析模型。故障电流由交流和直流两部分组成，定义如（5）所示。式中：E'为故障电流限制器模型连接点的网络相位电压；Z为故障点的戴维南阻抗；ω为电力系统频率；α和φ分别为故障时刻（零时）的电压相位角和网络阻抗相位角；R为戴维南电阻；L'为戴维南电感。

根据图4故障电流限制器的等效磁路可以计算得到磁通量。在图4中，Ra为故障电流限制模型的动铁芯（电枢）磁阻，Rc为故障电流限制模型的固定铁芯磁阻，Rg为故障电流限制模型的气隙磁阻设定值，F为故障电流限制模型等效磁通量。

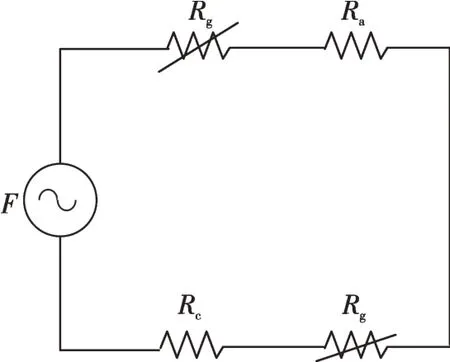
图4 故障电流限制器的等效磁路

式中：la、lc、lg分别为棒型移动铁芯、凹型固定堆芯和气隙的平均通径；Aa、Ac、Ag分别为凹型固定堆芯3个横截面的面积；μ和μ0分别为磁芯和空气的渗透系数。

对于图5 所示VFCL 模型实际结构的规定尺寸，上述参数可定义为：

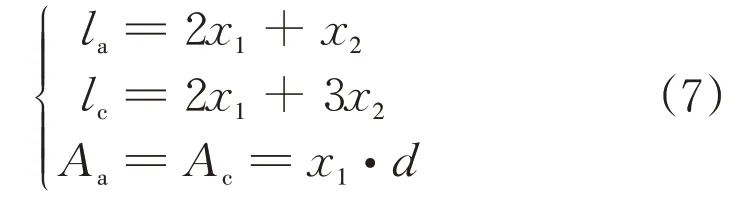
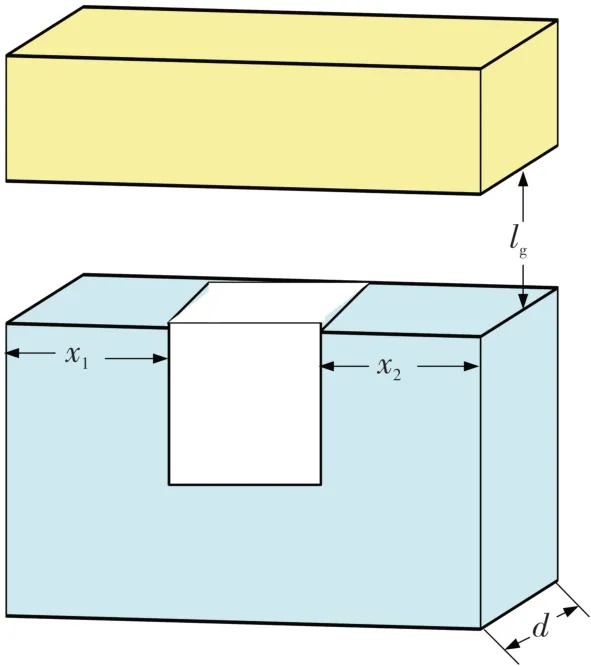
图5 VFCL模型实际结构

忽略边缘效应，则VFCL 模型芯材与气隙的横截面积相等，即：

为了分析VFCL 模型的电枢运动和反应器运行时间，采用牛顿定律对电枢运动和运行时间进行分析。

式中：Fmagnetic为VFCL 模型的电磁力；Fgravity为VFCL 模型的电枢重力；Fspring为VFCL 模型的弹簧力；Ma为VFCL 模型的电枢质量；g 为重力加速度；K为VFCL 模型的弹簧常数；Δx为VFCL模型的电枢位移。

基于VFCL模型的电磁力计算公式为：

式中：LVFCL为电枢电感；RVFCL为VFCL模型的磁阻；N为VFCL模型的绕组匝数。

通过计算VFCL 模型的电磁力，可以得到棒型移动铁芯的加速度，则棒型移动铁芯的位置可表示为：

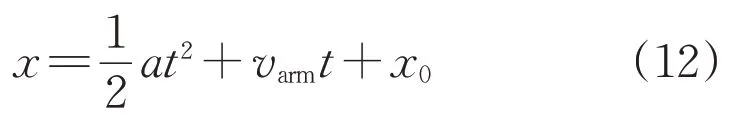
式中：a为棒型移动铁芯的加速度；x0为上一时刻棒型移动铁芯的电枢位置。

由于基于VFCL 模型电枢电流与移动时间和VFCL 模型气隙长度有关，因此电磁力和加速度在每一时刻都是不同的。因此，本文在计算故障电流限制器的运行速度和电流波形时，需在每步时间内计算上述方程。

2.2 遗传算法优化

尽管已经确定了故障电流限制器的总体物理结构，但故障电流限制器的细节部分还需要根据实际现场的工作电压阈值进行细微调整。遗传算法［29-31］通过模拟自然进化过程，寻找结构最优解。对结构对象进行操作，利用求导不限定性，通过概率化寻优方式，自动调节搜索方向，可以高效地确定故障电流限制器的细节部分。本文中的遗传算法主要包括目标函数确定和优化变量确定两个步骤，具体流程如图6所示。

图6 遗传算法优化过程

本研究采用理想的网络短路水平计算最终电感量，将初始值分配给优化变量，根据上述方程，利用轨迹值、VFCL 模型最终电感和故障电流，计算VFCL 模型的其他参数。同时，根据得到VFCL 模型参数，计算出VFCL模型的运行时间、体积和初始电感等目标函数。最后，使用遗传算法在训练迭代中改变路径，直至得到最优答案。

目标函数作为VFCL 模型实际使用的指标，用于评价VFCL 模型的占用空间、耐用性及电网短路水平。

为了使故障电流限制器具有最优的占用空间，需要在安全运行的前提下，得到VFCL 模型的体积最小值。

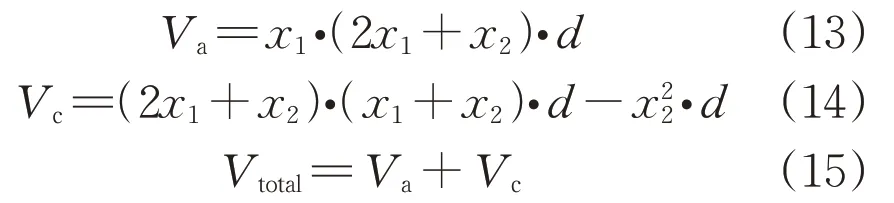
式中：Va和Vc分别为基于VFCL 模型的电枢和固定铁芯的体积；Vtotal为Va与Vc之和。

运行时间指棒型移动铁芯和气隙到达VFCL最小长度所花费的时间。为了使VFCL具有优良的耐用性，根据运行时间与故障电流限制器成正比关系，把故障电流限制器的运行时间应小于断路器的运行时间作为前提条件，通过运行时间Atime评价其耐用性。

基于短路前故障电流限制器电感应非常低，短路后应尽可能高的原则，在发生短路时，故障电流限制器电感的初始值和最终值之间的差值越大，其故障电流限制器的性能越好。由于故障电流限制器的电感最终值是根据所需故障电流限制器的网格短路水平和具体数量确定的，因此在目标函数中应考虑故障电流限制器的电感初值LVFCL。

最终得到VFCL 的目标函数Fcore，如式（16）所示。

式中：Vtotal为VFCL 模型的总体积；LVFCL为VFCL模型的初始电感；Atime为VFCL模型的运行时间；α、β、γ为遗传算法的有效系数，且α+β+γ=1。

在本阶段中，变量d被选为优化变量，并通过式（9）—（12）进行计算。

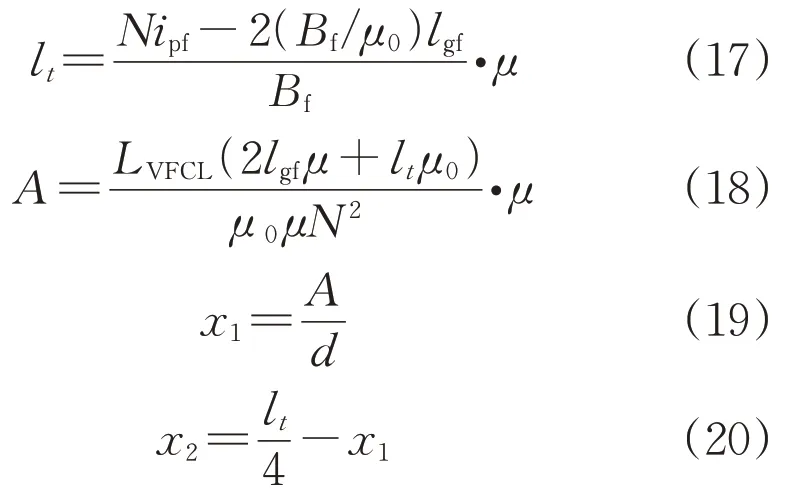
式中：lt为凹型固定堆芯中磁通路径的总长度；A为凹型固定堆芯的横截面积；Bf、lgf、ipf分别为电枢运动末端气隙磁通密度、最终气隙长度和电抗器电流的最终峰值。

除了目标函数的优化，VFCL 模型的初始气隙长度和最终气隙长度也应被视为遗传函数的优化变量。原因是这两个变量都会影响VFCL 模型的工作时间和初始电感，较大的初始气隙使得初始电感较小，但也会导致电磁力减小，从而使电抗器运行缓慢。

3 对比和仿真实验

3.1 对比实验

在一定的实验条件下进行仿真实验，具体如表1 所示。将VFCL 模型通过遗传算法进行优化操作，优化后VFCL模型的结构参数如表2所示。

表1 仿真环境

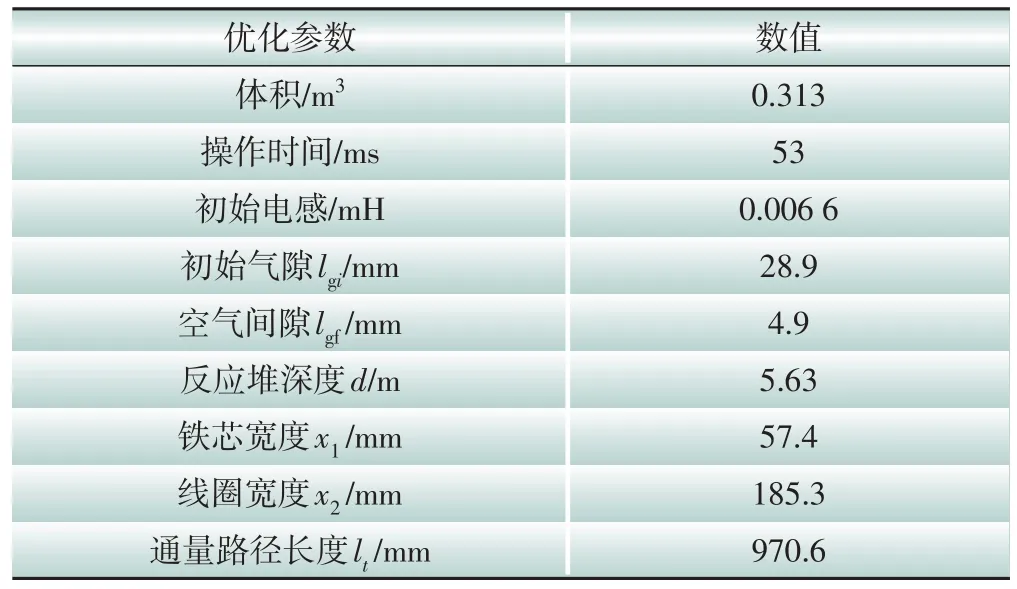
表2 遗传算法优化后的VFCL模型结构参数

3.2 仿真实验

为了验证分析结果，将遗传算法得到的最优模型参数与VFCL 结合，采用有限元方法对设计的VFCL 模型进行了模拟，并用2D Ansoft Maxwell 软件对VFCL 模型进行优化，生成最优参数与VFCL结合的网格区域，如图7所示。通过生成的网格区域可以看出，其气隙附近的网格很小，VFCL的磁通连接显示该反应器的漏磁非常低。