二分网络中基于增强动态距离模型的社团检测算法
2022-12-09苏思行陈碧连曹浪财
苏思行,陈碧连,曹浪财
(厦门大学航空航天学院,厦门市大数据智能分析与决策重点实验室,福建厦门361005)
现实生活中真实网络的一个基本组成部分是它们的底层社团[1].通常,一个社团被认为是内部紧密相连的一组节点,而不同社团之间的外部链接是稀疏连接的.一个网络可能包含多个社团,社团检测任务旨在网络中找到所有这些社团,也称为图聚类[2].
当前,许多研究主要集中在只包含一种节点类型的单模网络上.人们提出了许多方法来应对不同假设下识别单模网络的情况,如非负矩阵分解[3]、标签传播[4]和模块度优化[5]等.然而,真实世界的网络通常包含多种类型的节点,最简单的情况是包含两种不同类型节点的二分网络[6].投影方法是一个简单的解决方法,即将二分网络转换为单模网络,然后使用现有的社团检测方法[7].因为只有一种类型的节点被应用,而另一种类型的节点在投影后丢失,投影方法可能会导致信息不完整的问题[8],所以,学者开发了各种方法来在社团划分之后维护两种类型的节点.Barber[6]首先提出了一个二分模块度,然后开发了BRIM模型,将节点的两个独立部分归纳为模结构.但是,因为高模块度分数不能准确地检测到小社团,二分网络的模块度在分辨率问题[9]上存在局限性.于是,Sun等[10]将单模网络中的传统动态距离模型Attractor[11]扩展到二分网络中,提出二分网络的传统动态距离模型BiAttractor,能够准确地检测到小社团.但是,BiAttractor的敏感参数λ的微小变化可能会导致由此产生的群落结构的巨大差异,使得模型的鲁棒性差.
为了解决这个问题,本文提出一种新的局部非对称边缘聚类系数(local asymmetric edge clustering coefficient,LAECC),将自我中心(Ego-Leader)[12]从单模网络扩展到二分网络,计算专属邻居节点对距离的影响,以此用来摆脱敏感参数λ.在此基础上,基于Ego-Leader,本文在二分网络中设计了一个增强的动态距离模型E-BiAttractor,并提出了相应的社团检测算法.与传统动态距离模型相比,E-BiAttractor模型具有更好的性能和鲁棒性.
1 背景知识
在本节中,首先介绍本文会用到的二分网络符号定义.而后,介绍一种能够在二分网络中检测社团的传统动态距离模型BiAttractor[10].
1.1 符号定义
设G=(U,V,E)是一个无向无权的二分图,其中U和V代表两组不同类型的节点.在二分网络中,同一类型(U或V)的节点之间没有边连接.
定义1(节点u的邻居节点集合)节点u的邻居节点集合N(u)表示如下:
N(u)={v|u∈U,v∈V,(u,v)∈E}.
定义2(节点u的二阶邻居节点集合)节点u的二阶邻居节点集合NN(u)表示如下:
NN(u)={y|x∈N(u),y∈N(x),u∈U,x∈
V,y∈U,u≠y}.
定义3(专属邻居节点集合)对于边e(u,v)而言,节点u的专属邻居节点集合定义为NE(u)=N(u)-{v}.
定义4(Jaccard距离)使用流行的Jaccard距离[13]来量化两个同类型节点u和节点x之间的距离,定义如下:
(1)
定义5(局部Jaccard距离)由于二分网络的性质[10],不同类型节点之间没有公共邻居, Sun等[10]提出能够计算二分网络中直接相连的不同类型节点之间距离的局部Jaccard距离,定义如下:
(2)
1.2 二分网络中的传统动态距离模型
Sun等[10]提出一种能够在二分网络中检测社团的传统动态距离模型BiAttractor,它通过检查节点之间距离的变化(即动态距离),来发现二分网络中的社团.其基本思想是每个节点与其邻居节点交互,最终形成稳定分布,即同一社团的节点彼此靠近,不同社团的节点彼此远离.
BiAttractor有两种不同的交互模式,包括直接连接节点对距离的影响和专属邻居节点对距离的影响.
模式1:直接连接节点的影响.
在动态交互过程中,直接连接节点的影响ID(u,v)使节点u和节点v之间的距离减小,定义如下:
ID(u,v)=
(3)
其中,f(·)是一个耦合函数,可用正弦函数sin(·)来计算[10],deg(u)表示节点u的度数.
模式2:专属邻居节点的影响.
在动态交互过程中,每个专属邻居节点会吸引与它相连的节点(节点u或节点v)向自身移动.通过引入一个参数λ来判断节点u的专属邻居节点x会对节点u和节点v之间的距离产生积极影响还是消极影响.定义如下:
ρ(x,u)=
(4)
在上式中,ρ(x,u)表示节点u的专属邻居集NE(u)里的节点x将会对距离d(u,v)产生积极影响还是消极影响,参数λ的取值推荐为[0.2,0.8][11].
专属邻居节点的影响IE(u,v)的定义如下:
(5)
最后,节点u和节点v之间的距离d(u,v)随时间的变化如下所示:
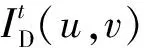
2 二分网络中的增强动态距离模型
2.1 局部非对称边缘聚类系数
Cai等[12]在单模网络中提出非对称边缘聚类系数(asymmetric edge clustering coefficient,AECC).对于连接节点u和节点v的边e(u,v),AECC定义为:
为了将AECC从单模网络扩展到二分网络,本文提出LAECC.直接相连的节点u对节点v的LAECC定义为:
(6)
其中,N(x)表示节点x的邻居节点集合,NE(u)表示节点u的专属邻居节点集合.CLAECC(u,v)首先计算NE(u)里每个节点对节点v的CAECC之和,再除以节点u的专属邻居节点个数|NE(u)|.需要注意的是,节点u对节点v的CLAECC不等于节点v对节点u的CLAECC,即CLAECC(u,v)≠CLAECC(v,u).
2.2 Ego-Leader和它的特征
一个节点的Ego-Leader由一个或多个LAECC最大的邻居节点组成,任何一个节点的Ego-Leader包含的节点数永远不会超过该节点的邻居数.从节点的邻居集合中选择具有最大LAECC的节点来形成它的Ego-Leader,当多个邻居节点对该节点具有相同的最大LAECC时,这几个邻居节点都会被选取.因此,本文利用LAECC来寻找二分网络中任意节点的Ego-Leader.
判断节点u的专属邻居节点x对节点u和节点v之间距离的影响时,本质是判断节点x和节点v是否相似[11].Cai等[12]提出,当节点u的专属邻居节点x和节点v的Ego-Leader有共同节点时,认为节点x和节点v是相似的.
因此,若节点x和节点v的Ego-Leader有共同节点,则节点x作为节点u的专属邻居节点,会对节点u和节点v的距离d(u,v)产生积极影响,使得节点u和节点v的距离在交互过程中减小.相反,若节点x和节点v的Ego-Leader没有共同节点,则节点x作为节点u的专属邻居节点,会对节点u和节点v的距离d(u,v)产生消极影响,使得节点u和v的距离在交互过程中增大.
除此之外,Ego-Leader还具有以下重要特征:
1) Ego-Leader是不对称的.节点u在节点v的Ego-Leader中,不代表节点v也在节点u的Ego-Leader中.
2) Ego-Leader是局部和静态的.一个节点的Ego-Leader由其邻域集合中LAECC值最大的节点组成.也就是说,任何Ego-Leader都只适用于一个节点,它的活动范围是该节点的邻居节点集合.因此,Ego-Leader强烈依赖于网络拓扑结构.因为网络拓扑结构是静态的,所以节点的Ego-Leader也是静态的,不会发生任何变化[14].
2.3 交互模式
E-BiAttractor和BiAttractor一样,只讨论两种交互模式,直接连接节点对距离的影响和专属邻居节点对距离的影响.
模式3直接连接节点的影响.
与BiAttractor的模式1相同.由式(3)可知,在动态交互过程中,因为节点u和节点v是相连的,所以节点u和节点v会相互靠近,直接连接节点的影响ID(u,v)使节点u和节点v之间的距离减小.
模式4专属邻居节点的影响.
为了提高模型的鲁棒性,同时说明专属邻居节点对距离产生的是积极影响还是消极影响,本文利用能够应用于二分网络的LAECC,计算每个节点的Ego-Leader,来代替内聚参数λ.对于e(u,v),节点x属于节点u的专属邻居节点集合NE(u),通过判断节点x的Ego-Leader和节点v的Ego-Leader是否有重叠部分,以此来判断节点x和节点v是否相似.定义如下:
σ(x,u)=
(7)
其中,Ego(x)表示节点x的最高LAECC的邻居节点集合.函数σ(x,u)不仅表示了节点u的专属邻居节点x对距离的影响方向(积极或消极),而且还表示了这种影响的强度.如果节点u的专属邻居节点x与节点v的Ego-Leader有公共节点,那么节点u到它的专属邻居节点x的移动会导致d(u,v)的减小,即节点u的专属邻居节点x对距离会产生积极影响;相反,如果节点u的专属邻居节点x与节点v的Ego-Leader没有公共节点,那么节点u到它的专属邻居节点x的移动会导致d(u,v)的增加,即节点u的专属邻居节点x对距离会产生消极影响.
结合函数σ(x,u),专属邻居节点对距离的影响IE定义如下:
(8)
最后,综合考虑这两种交互模式,节点u和节点v之间的距离d(u,v)随时间的变化如下所示:
(9)
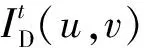
2.4 算法流程
基于E-BiAttractor的社团检测算法流程如下所示:
算法:基于E-BiAttractor的社团检测算法
输入:无向无权的二分图G=(U,V,E).
输出:二分图G的k个社团C1,C2,…,Ck.
1) 开始时间(t=0),对于每条边e(u,v)∈E,利用式(2)计算每条边的初始距离.同时,利用式(6)计算每条边的两个LAECC,最后得到每个节点的Ego-Leader.
2) 对于每条边e(u,v)∈E,如果t时刻e(u,v)的距离dt(u,v)大于0且小于1,则利用式(3),(7),(8),(9)计算出t+1时刻e(u,v)的新距离dt+1(u,v);如果t时刻e(u,v)的距离dt(u,v)小于0或大于1,则这条边达到收敛,跳过这条边.
3) 重复步骤2)直到所有边都收敛.
4) 删除距离大于1的边,检测出网络的群落结构,得到社团C1,C2,…,Ck.
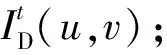
2.5 时间复杂性
算法的时间复杂度分为三部分.首先,计算每条边的初始距离,时间复杂度为O(|E|),其中|E|为边数.而后,计算每个节点的Ego-Leader,时间复杂度为O(2·|E|).最后,每次交互的时间复杂度是O(N·|E|),其中N是两个相连节点的专属邻居节点的平均数,动态交互过程的时间复杂度为O(T·N·|E|),T表示时间步长.因此,算法的时间复杂度为O(T·N·|E|).
3 实验结果及分析
本节首先介绍实验准备(数据集、对比算法和评价指标),而后将基于E-BiAttractor模型的社团检测算法与另外3种算法在8个公开数据集上进行对比实验,通过对实验结果的分析,验证基于E-BiAttractor模型的社团检测算法的有效性.
3.1 实验准备
3.1.1 数据集介绍
在对比实验中,本文使用http:∥konect.cc/networks/上的8个常见的无标签公开数据集,这8个公开数据集的节点数、边数以及节点的平均度在表1中详细给出.
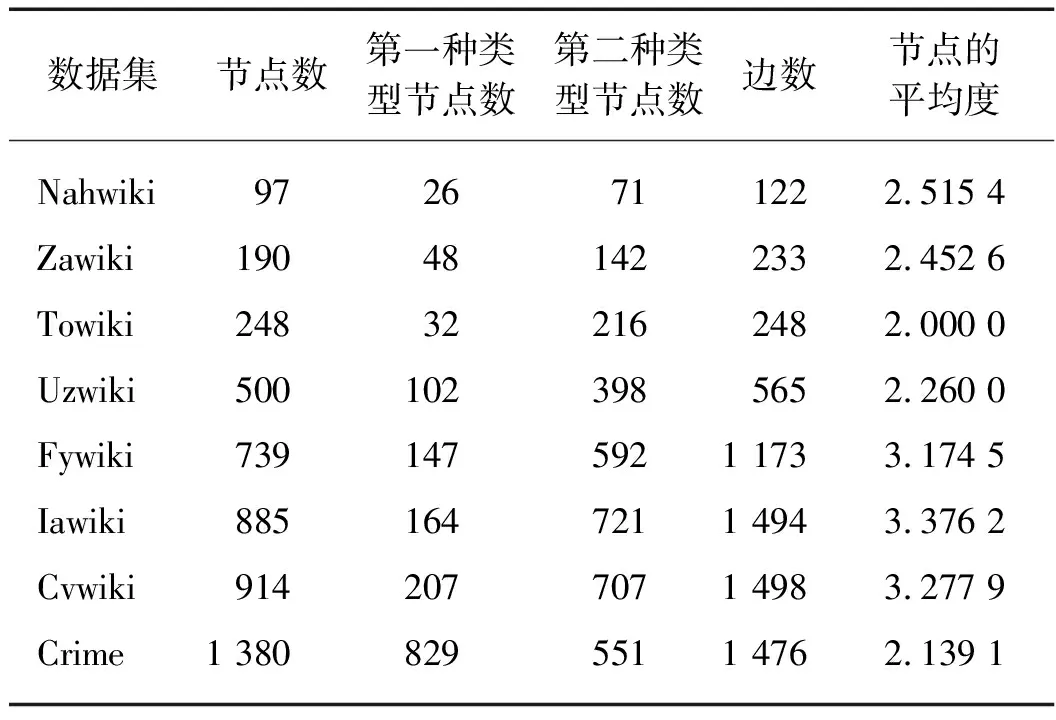
表1 数据集的简要信息
3.1.2 对比算法介绍
为了对基于E-BiAttractor模型的社团检测算法的性能有个客观认识,将它与基于BiAttractor的社团检测算法[10]、基于Adaptive Brim的社团检测算法[6]和基于LP Brim的社团检测算法[15]这3种算法进行比较.实验中,将BiAttractor需要用到的参数λ设为0.8.
3.1.3 评价指标介绍
因为所有网络都是无标签的,本文采用模块度(modularity)[16]来衡量检测出来的社团质量.其定义为:
(10)
其中:m表示网络中的边数;A是网络的邻接矩阵,如果节点i和节点j之间有边,则Ai,j=1,否则Ai,j=0;deg(i)表示节点i的度数;ci表示节点i所处的社团,如果节点i和节点j被分配到同一个社团,则δ(ci,cj)=1,否则δ(ci,cj)=0.该指标的范围在0到1之间,值越大,说明社团检测算法的性能越好.
3.2 实验结果分析
表2描述的是各个模型在各个数据集上的模块度表现情况.实验结果中的评价指标用粗体表示最好的结果,下划线表示次好的结果.从表2中可以得到如下结论:
1) E-BiAttractor在这8个数据集中,有5个数据集(Nahwiki、Zawiki、Towiki、Cvwiki、Crime)取得最好的结果,有两个数据集(Fywiki、Iawiki)取得次好的结果,说明E-BiAttractor较之其他3种算法,能够更有效的区分社团;
2) 在这8个数据集中,E-BiAttractor都取得了比BiAttractor更好的结果,而且E-BiAttractor不需要修改参数,说明通过引入Ego-Leader,E-BiAttractor较之BiAttractor具有更好的鲁棒性.
综上所述,本文提出的E-BiAttractor通过LAECC寻找出各节点正确的Ego-Leader,借此来判断两个节点是否相似,使得E-BiAttractor免于调参,并适用于绝大部分网络,具有更好的鲁棒性,因此在区分社团上有更优异的表现.
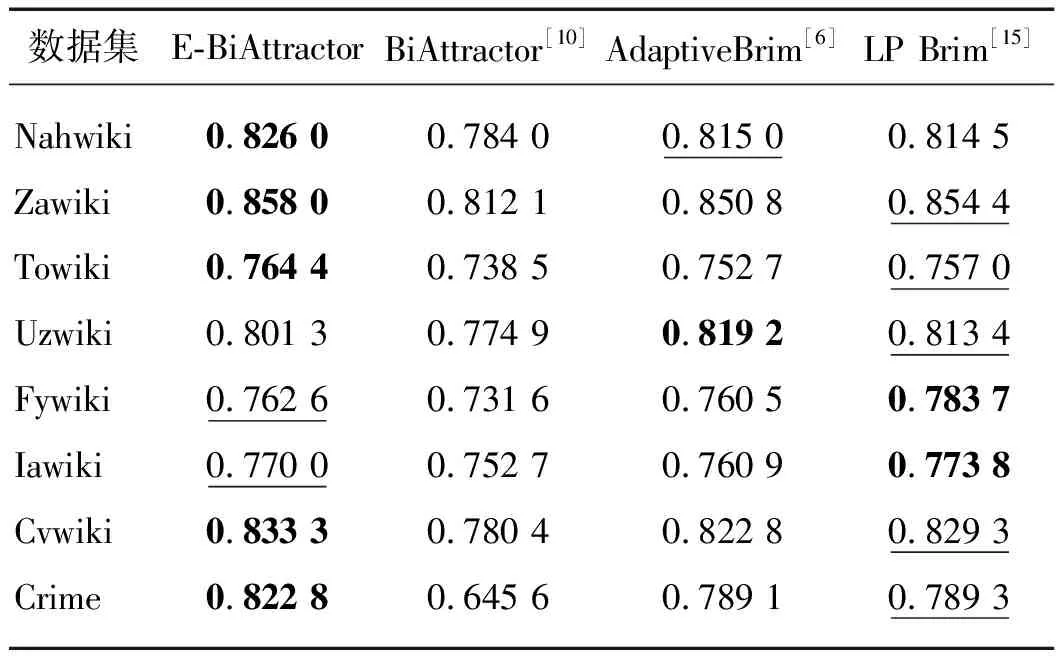
表2 各算法的模块度比较
4 结 论
动态距离模型是一种成熟的社团检测方法,可以有效地区分社团,进而实现社团内部紧密连接、社团之间稀疏连接的目的.二分网络中的社团检测算法相比于单模网络中的社团检测算法更加富有挑战性.
本文提出一种在二分网络中基于Ego-Leader进行社团检测的增强动态距离模型E-BiAttractor,它利用LEACC得到Ego-Leader,通过分析节点间的Ego-Leader,来提升动态距离模型在二分网络中的鲁棒性和有效性.在8个数据集中进行对比实验,实验结果表明,本文提出的算法与其他3种社团检测算法相比,模块度都有一定程度的提升,模型具有更高的精度,且没有参数,具有很高的鲁棒性.
