奈奎斯特判据在时滞对象自抗扰控制中的应用
2022-12-09金辉宇兰维瑶李智斌
金辉宇,倪 刚,兰维瑶,李智斌
(1.厦门大学航空航天学院,福建厦门361102;2.新华三技术有限公司,浙江杭州310051;3.山东科技大学电气与自动化工程学院,山东青岛266510)
2022年是厦门大学控制科学与工程学科成立50周年,也是奈奎斯特发表文献[1]90周年.该文提出了基于频率响应分析反馈系统稳定性的图形化判据,该判据为控制系统的分析和设计提供了新方法,标志着频域方法的成熟和古典控制时期的到来.此后,这一判据被称作奈奎斯特判据,成为古典控制的核心内容,在自动控制的理论研究、工程实践和教学中发挥着重要作用.而文献[1]也入选控制理论历史上最重要的25篇文献,并因为发表时间而位居第一[2].
然而,20世纪60年代现代控制理论兴起后,整个古典控制不再时髦,甚至被误解为简单、过时.奈奎斯特判据也就随之被冷落,在教学和科研中的地位不断降低.目前,国内通常仅在本科阶段学习奈奎斯特判据,研究生阶段不再系统讲述,转而强调状态空间方法.这就导致作为科研主力的研究生们总体上不熟悉奈奎斯特判据,难以用它解决面对的科研问题.而这又进一步加剧了“简单、过时”的误解,甚至还要加上“无用”.奈奎斯特判据陷入了“被误解—不被重视—难以应用—误解加深”的正反馈,其研究日渐衰微.
与状态空间方法相比,奈奎斯特判据有其独特的优势.它巧妙地平衡了数学严谨和工程直观.它以复变函数理论为基石,充分严谨,常常能得到稳定性的充要条件;它以图形为主要分析手段,足够直观,便于工程技术人员接受.它一般不需要繁杂的数学运算,过程简洁明了,特别适合研究低阶单输入单输出对象.
为体现奈奎斯特判据的优势,本文用它研究时滞对象的自抗扰控制(active disturbance rejection control,ADRC).ADRC是韩京清研究员[3-5]提出的一种通用控制技术.它汲取了PID控制的思想精华,具有结构简单、调参方便、鲁棒性好、适用面广等优点.它以“内扰”来描述对象的不确定性,并将内扰和外扰归结为总扰动,再构造扩张状态观测器(extended state observer,ESO)实时估计总扰动,最后用反馈予以补偿,从而实现“自抗扰”.由于统一处理内、外扰,ADRC不依赖对象的数学模型,在克服对象不确定性和抑制外扰方面具有独特的优势.21世纪以来,ADRC蓬勃发展,在工业过程、伺服系统、汽车工业和航空航天等领域不断取得成功应用[6-7].受应用研究的激励,ADRC的理论研究也日趋活跃,成为当时一个热点[8-10].
在工业过程领域,由于存在传输时滞、容积时滞、测量时滞等因素,被控对象常常是时滞对象.ADRC高度重视时滞对象,发展出无视时滞法、阶次提高法、时滞预估法等若干种控制时滞对象的方法,在工程实际中取得了良好的效果[11-12].但时滞对象ADRC的理论研究相对滞后,直到近年才找到若干稳定性条件[13-14].目前,时滞对象ADRC稳定性研究的主要工具是时滞常微分方程稳定性理论,这一时域方法可以得到严格、精巧的理论结果,但存在理论艰深、学习困难的缺点.
本文用奈奎斯特判据重新研究了一阶时滞对象在ADRC下的稳定性.所研究问题的特点是,对象不稳定或临界稳定,ADRC中采用降阶ESO.这两点增加了问题的难度,一度被认为难以用传递函数方法研究[14].本文先进行框图化简,将原问题分母中的超越函数项分离出来,成为时滞对象反馈控制的标准形式.再分情况绘制奈奎斯特图分析稳定性,得到了与文献[14]一致的充要条件.这表明,奈奎斯特判据是研究ADRC的有力工具.
1 奈奎斯特判据简介
考虑图1(a)所示的反馈控制系统,其中r与y分别参考信号与输出,G(s)与F(s)分别是前向通道和反馈通道的传递函数.该系统的稳定性取决于特征方程
1+G(s)F(s)=0
(1)
根的位置.当且仅当所有的根都在开左半平面(left-half-plane,LHP)时,系统是稳定的.
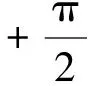
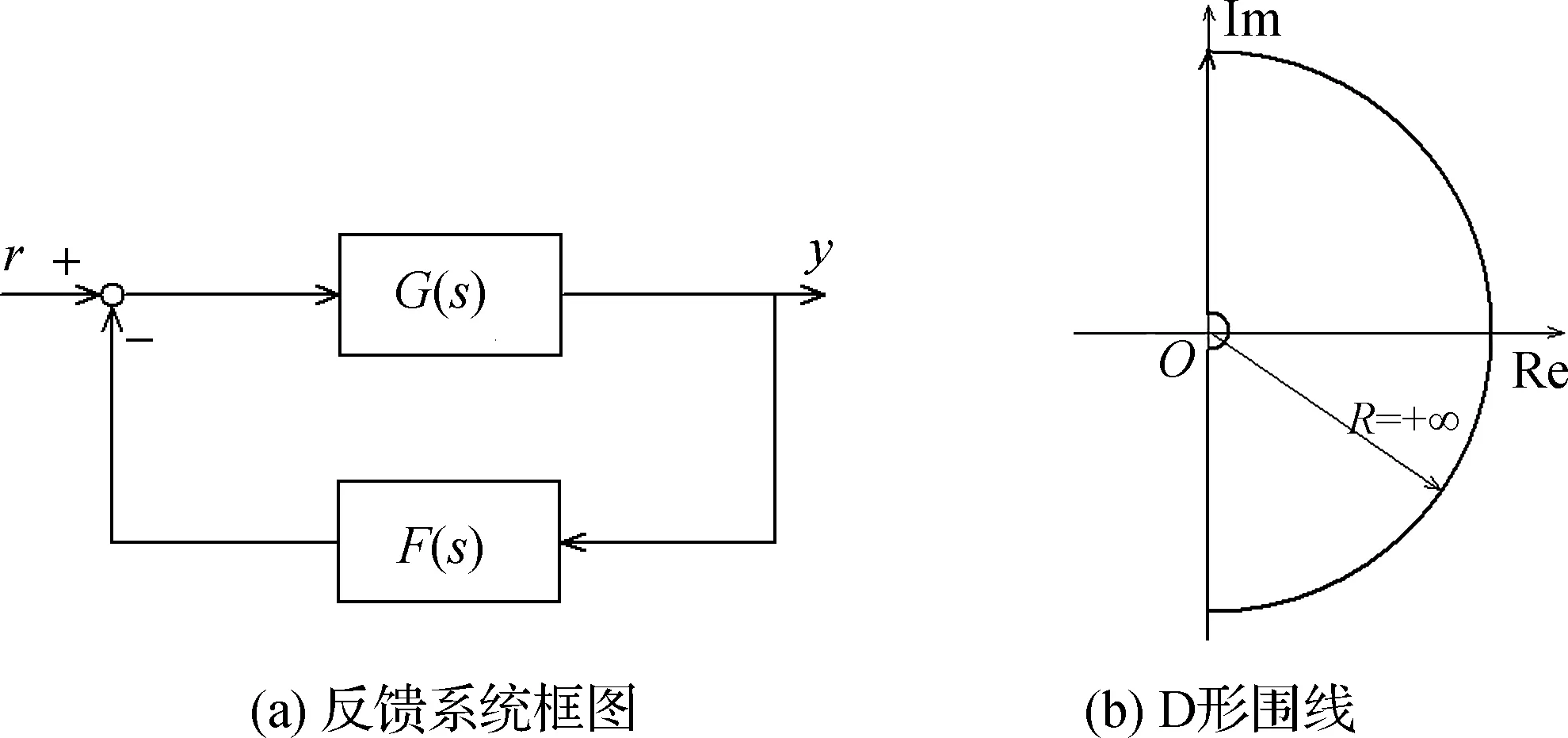
图1 反馈系统和D形围线Fig.1Feedback system and D contour
假定奈奎斯特曲线顺时针N次包围点-1+i0,而G(s)F(s)在右半平面有P个极点.奈奎斯特判据断言,方程(1)的全部根中,不在LHP的根有Z=N+P个.显然,当且仅当Z=0时,反馈系统稳定.
奈奎斯特判据适用于时滞对象[15].其详细介绍和绘图细节可见文献[16-17].
2 理论结果
2.1 问题描述
设有一阶时滞对象
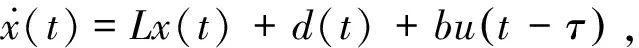
(2)
其中,u和x分别是对象的输入与输出,d是外部扰动,常数L,b,τ的数值已知,且满足L≥0,b,τ>0.控制器设计的目标是跟踪参考信号r.典型的r是一个阶跃信号.
为实现这一目标,文献[14]设计了降阶ESO
(3)
和控制器
(4)
问题是分析由式(2)~(4)组成的一阶LADRC系统的稳定性.
注1式(3)被称作降阶ESO的原因是它的微分方程只有一阶,而一般针对式(2)设计的ESO为两阶.
2.2 框图及其简化
线性自抗扰控制(LADRC)系统(2)~(4)有框图如图2[14]所示,其中
(5)
(6)
(7)
由于控制器C(s)的分母是超越函数,其稳定性分析被认为是一个难题.
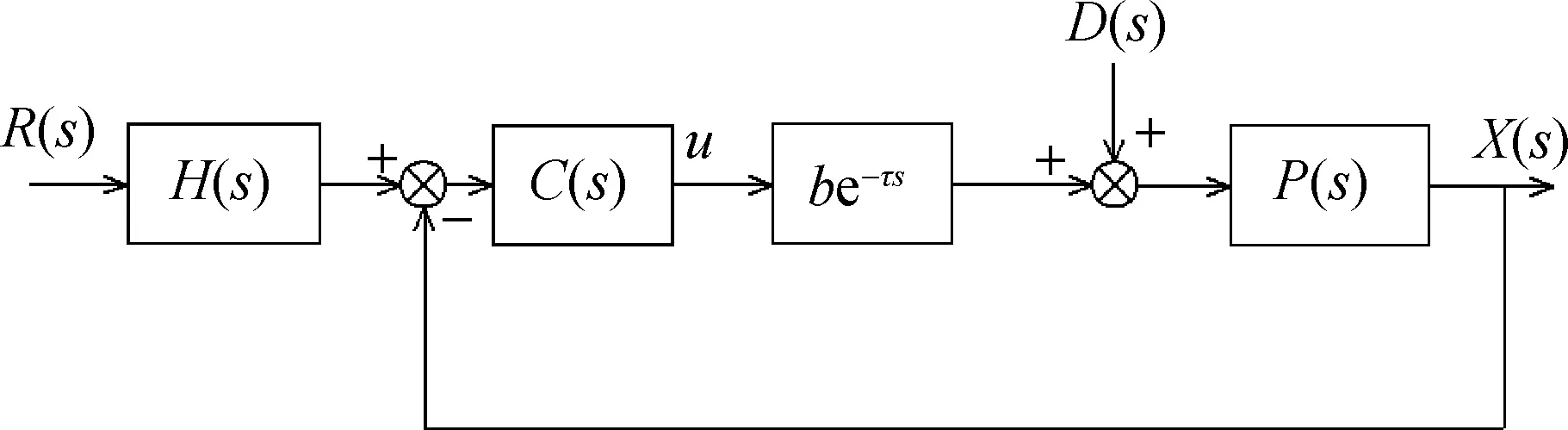
图2 LADRC系统(2)~(4)的框图[14]Fig.2Block diagram of LADRC system (2)~(4)[14]
现在化简图2.由于外扰不影响线性时不变(linear time-invariant,LTI)系统的稳定性,将D(s)删去.考虑到图3所示模块有传递函数
(8)
则图2可以化简为图4(e),中间过程见图4(a)~(d).
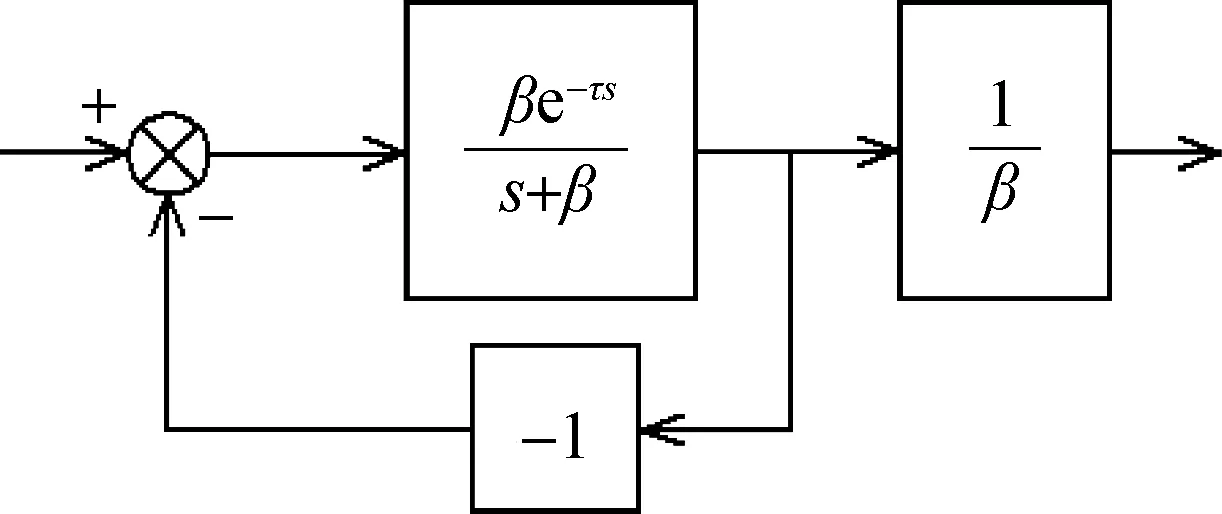
图3 一个具有传递函数(8)的模块Fig.3A block with transfer function (8)

图4 化简图2结果Fig.4Simplification of Figure 2
2.3 增益穿越频率
图4(e)中的反馈回路有传递函数
(9)
其特征方程为
(s+β)(s-L)+(ks+kβ+βL)e-τs=0.
(10)
注意到式(10)也是图2的特征方程,这再次表明图2和图4(e)的稳定性相同.
引理1假设k,β>0,考虑式(9)和方程
|W(iω)|=1.
(11)
方程(11)有4个根,其中有且仅有一个正实根
ωc=
(12)
证明方程(11)可以改写为
两边平方后得
ω4+(β2+L2-k2)ω2-(k2β2+2kβ2L)=0.
它有两个实根ω1,2=±ωc和两个虚根,其中有且仅有ωc是正实根.
引理1表明,当s从原点出发运动到+i∞的过程中,仅在ωc处穿越单位圆一次.在古典控制中,ωc被称作增益穿越频率,它是用奈奎斯特图分析稳定性时的一个关键参数.
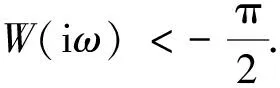
证明由式(9),有
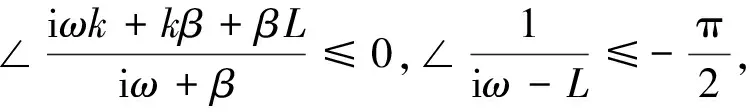
2.4 稳定性条件
现在建立稳定性条件.
定理1考虑由式(2)~(4)组成的一阶LADRC系统,假定k+β>L.记时滞上界
τ*=
(13)
该LADRC系统稳定的充要条件是时滞τ<τ*.
证明分别考虑L=0和L>0两种情况.L=0时,式(9)简化为
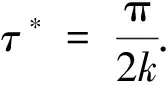
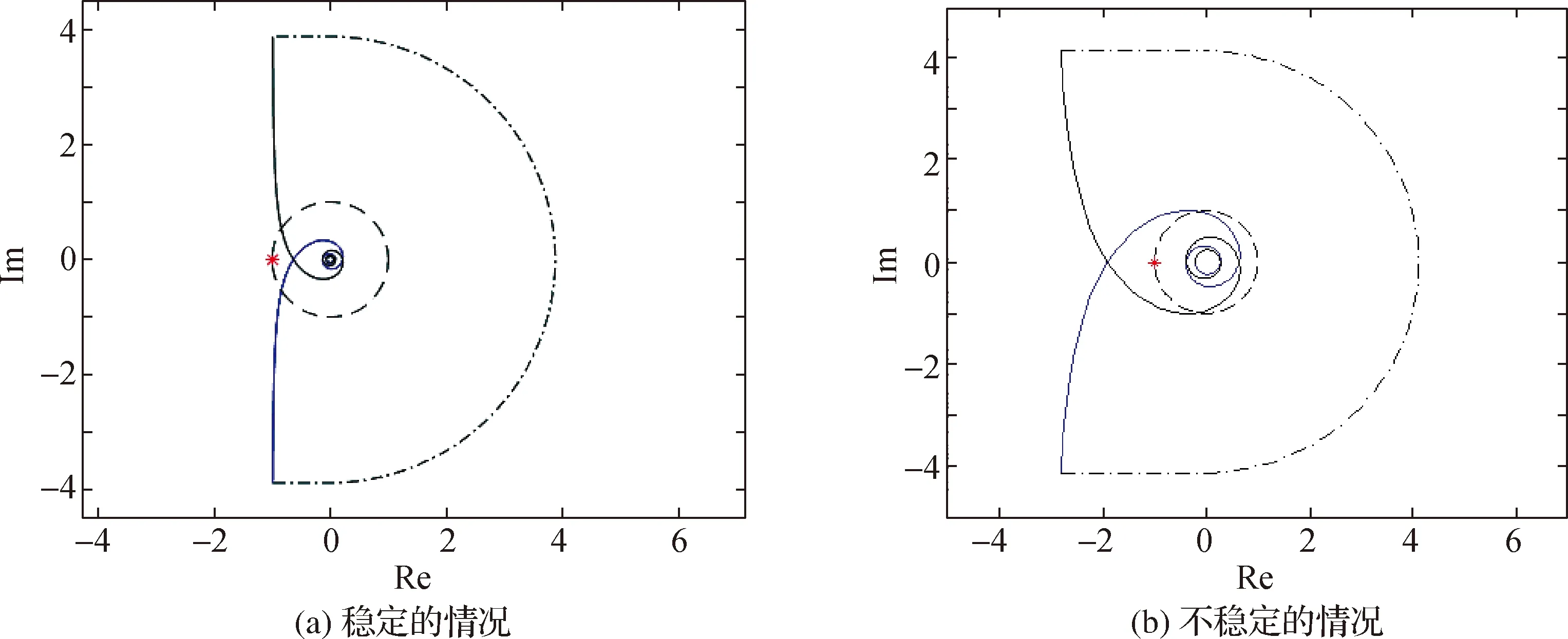
图5 L=0时W(s)的奈奎斯特图Fig.5Nyquist diagram of W(s) when L=0
下面证明不包围点-1的充要条件就是τ<τ*.分析W(s)的奈奎斯特曲线,当ω=0+时,W(iω)在-i∞附近;随着ω的增加,在ω=ωc处穿越单位圆;此后保持在单位圆内.当且仅当τ<τ*时,有
(14)
由引理2,W(s)的奈奎斯特曲线在第二象限穿入单位圆.此时整个奈奎斯特图不包围-1点,如图5(a)所示,其中蓝色实线是s从i0+出发运动到+i∞的曲线,黑色实线是s从-i∞沿负虚轴运动到i0-的曲线,而点划线大半圆是图1(b)中D形围道绕开原点的那一段小半圆生成的.
而当τ≥τ*时,式(14)不成立,系统不是稳定的.图5(b)是一个不稳定的例子,W(s)的奈奎斯特曲线顺时针包围点-1一次.
当L>0时,W(s)在原点无极点,D形围道不需要绕开原点.同时W(s)在右半平面有一个极点,由奈奎斯特判据,系统稳定当且仅当奈奎斯特曲线逆时针包围点-1一次.
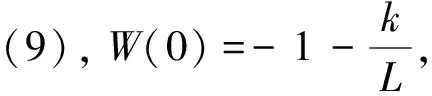
W(iωc)>-π
(15)
时,奈奎斯特曲线在第二象限穿入单位圆,逆时针包围-1点一次,如图6(a)所示.其中蓝线是从外向内穿入单位圆,而黑线是从内向外穿出单位圆.如果不等式(15)不成立,ADRC系统不是稳定的.图6(b)是一个不稳定的例子,奈奎斯特曲线顺时针包围点-1一次.
而不等式(15)成立的充要条件就是τ<τ*.因为
-∠(iωc-L)=-π+∠(iωc+L),
而
∠W(iωc)=∠(ikωc+kβ+βL)-∠(iωc+β)-
∠(iωc-L)-τωc,
于是不等式(15)等价于
τωc<∠(ikωc+kβ+βL)-∠(iωc+β)+
∠(iωc+L).
而由于
∠(ikωc+kβ+βL)-∠(iωc+β)+∠(iωc+L)=
∠(ikωc+kβ+βL)(iωc+L)(-iωc+β)=
ωcτ*,
当且仅当τ<τ*时,不等式(15)成立.
综合L=0和L>0两种情况,定理1得证.
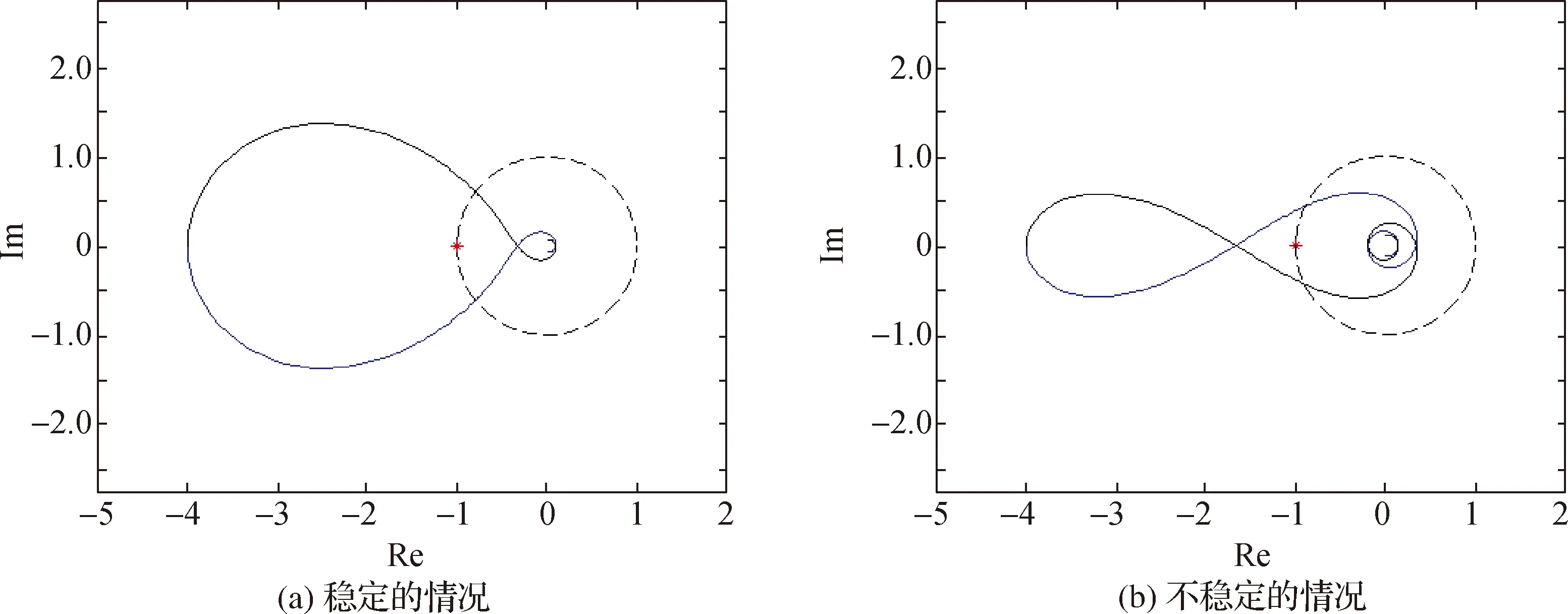
图6 L>0时W(s)的奈奎斯特图Fig.6Nyquist diagram of W(s) when L>0
3 讨论与算例
3.1 与文献[14]的比较
定理1得到的时滞上界和文献[14]一致,这表明了奈奎斯特判据的有效性.但定理1和文献[14]存在若干差别,在此进行比较.
从方法看,本文的主要方法是奈奎斯特判据,文献[14]的主要方法是时滞微分方程的稳定性理论.两种方法都能得到正确的结果,但奈奎斯特判据为自动化背景的研究人员所熟悉,数学专业的未必熟悉;时滞微分方程理论则相反,为数学背景的研究人员所熟悉,但自动化专业的常不熟悉.
从证明过程看,本文需要分别讨论L=0和L>0两种情况,不如文献[14]数学上简洁.但从工程的角度,L=0意味着对象临界稳定且包含一个积分器,而L>0意味着对象不稳定且不包含积分器,两者的差别明显而重要.因此,分情况讨论在工程上是合理的.
从结果来看,本文没有对外扰d作假设,而文献[14]假设d的极限存在且为一个有界常数.这一假设对于稳定性无必要,因为对象和ADRC都是LTI的,整个LADRC系统也是LTI的,而LTI系统的稳定性与外扰无关.这个假设是为了保证d能被完全兑消.
3.2 算例
本节通过两个算例说明定理1.
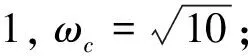
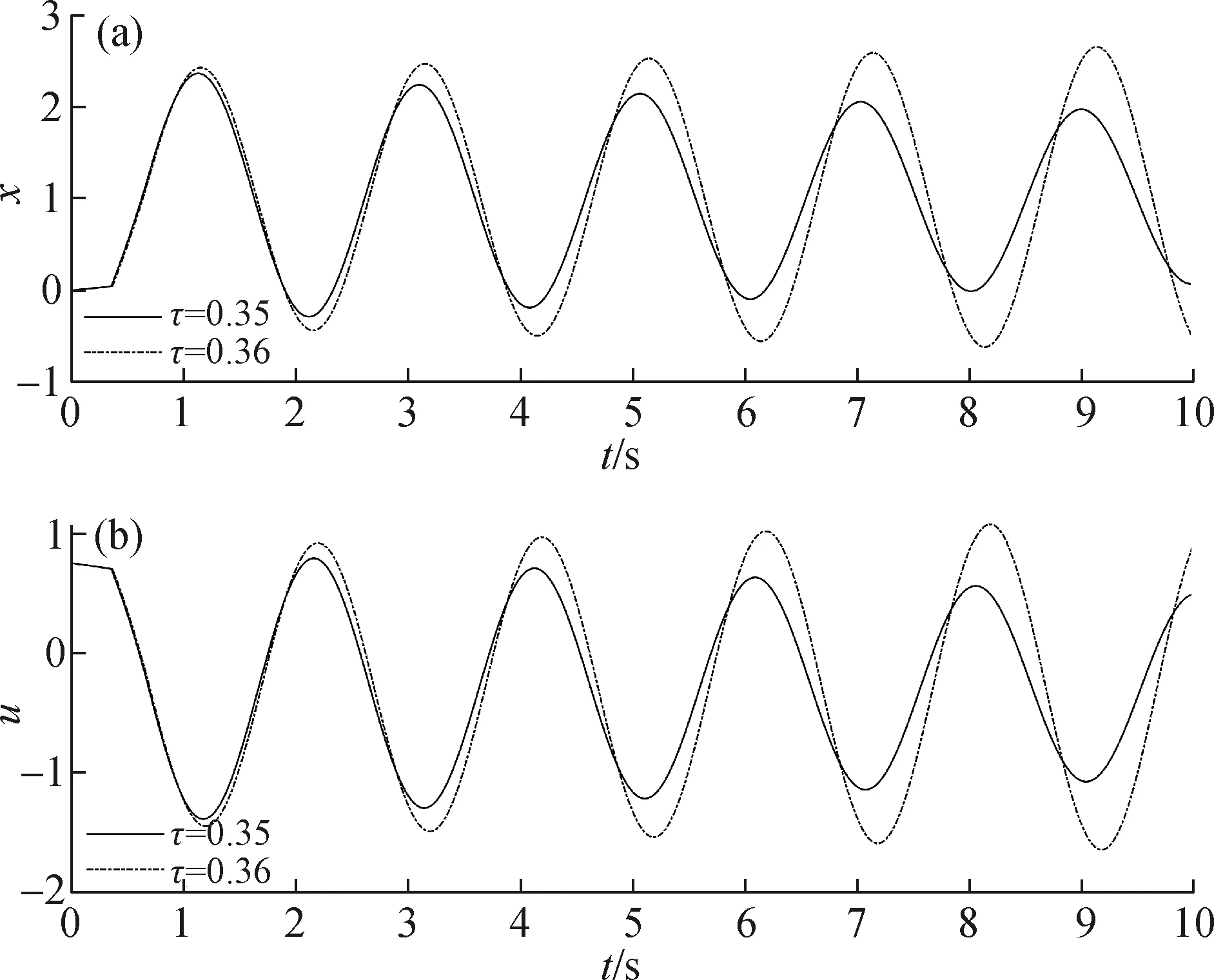
图7 例1的输出x(a)和控制u(b)Fig.7The output x(a) and control u(b) of example 1
例2仍取L=1,b=4,β=2,k=3.令τ=0.15,外扰取d1(t)=0.1·1(t)和d2(t)=0.1sin(2t)·1(t).用MATLAB数值求解方程(2)~(4),结果如图8.从图8中可以看到,两种情况系统都是稳定的,差别在于,d1(t)完全被兑消,而d2(t)没有被完全兑消,导致x和u在暂态结束以后仍存在振荡分量.
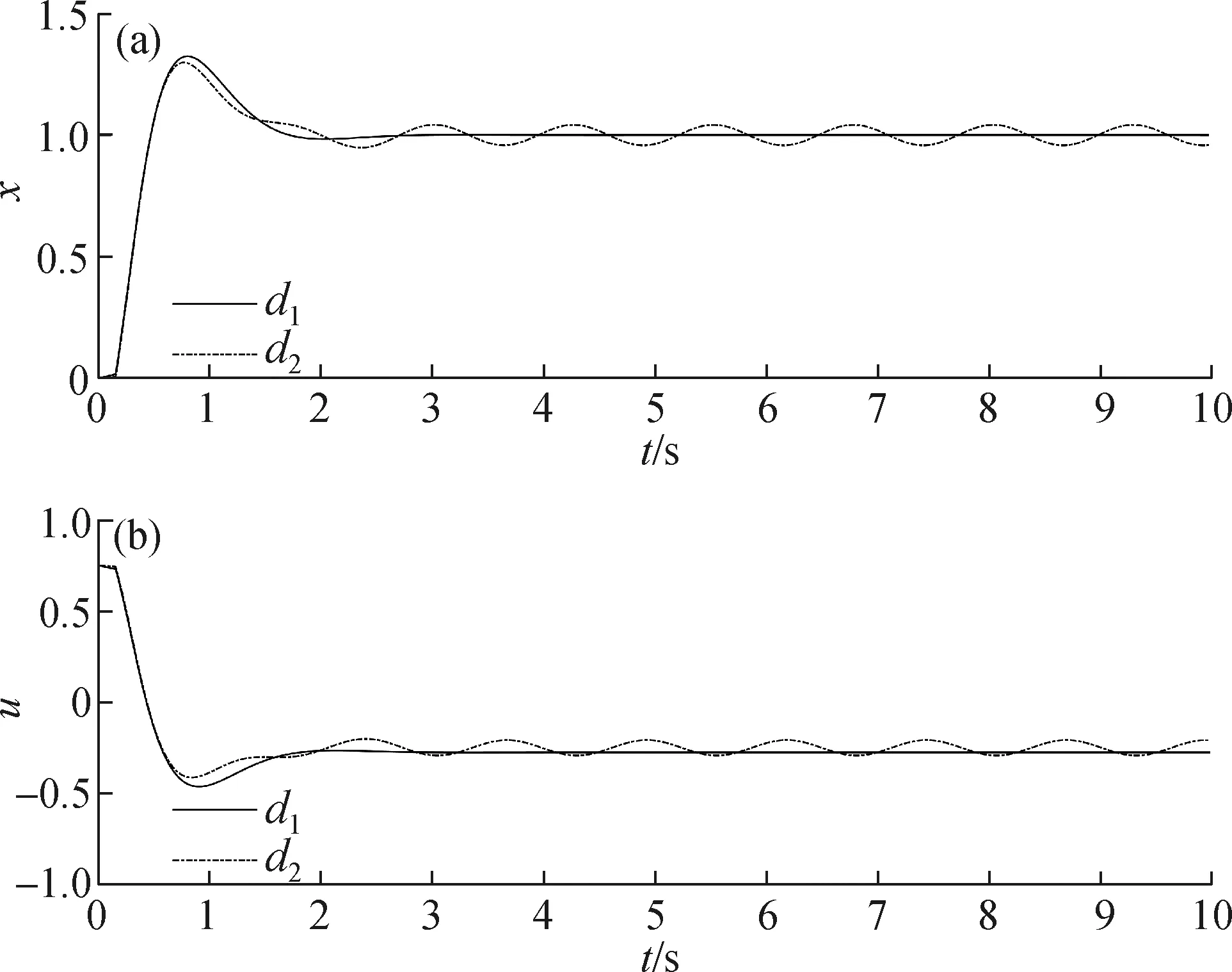
图8 例2的输出x(a)和控制u(b)Fig.8The output x(a) and control u(b) of example 2
4 结 论
本文以奈奎斯特判据研究时滞对象自抗扰控制的稳定性,得到了和文献[14]定理1一致的充要条件,并且放松了对外扰的要求.这表明,奈奎斯特判据并未过时,仍可以在控制理论的前沿研究发挥作用.为更好地发挥其作用,有必要加强奈奎斯特判据和整个古典控制理论的教学,尤其是研究生阶段的教学.
