基于GA-VMD-BiLSTM算法的风电功率预测
2022-12-09傅晓锦刘明旺
丁 同,傅晓锦*,刘明旺
(1.上海电机学院机械学院,上海 201306;2.中国铁塔股份有限公司宿迁市分公司,江苏 宿迁 223800)
目前,全球风电容量持续增长[1],风力发电占据电力系统的重要地位.为了平衡电力供需,须准确预测风电功率,以便配合热能系统和能量存储系统的整合调度.由于自然风易受气象条件影响,具有随机性,难以预测短期内风力发电量,极大削弱了风力发电的市场竞争力[2].因此,提高风电功率预测(wind power prediction,WPP)的准确性,可为能量平衡计算和功率调度提供有效信息,降低风电波动对能量系统的影响[3].
近年来,国内外专家学者对风电预测进行了广泛研究.Huang等[4]采用卷积神经网络(convolutional neural network,CNN)结合最小二乘法和批标准化(batch normalization,BN)处理数据并建立预测模型,模型精度显著提升,但未能很好剔除无效数据;李文武等[5]将变分模态分解(variational mode decomposition,VMD)分解后的数据作为输入,提高了预测精度,但无法体现数据内在特征;刘帅等[6]利用自回归滑动平均模型(auto regressive moving average model,ARMA)修正预测值,预测效果较好,但数据预处理时须依据经验选取临界率;文孝强等[7]利用经验模态分解(empirical mode decomposition,EMD)与蚁群优化算法建立预测模型,预测精度有所提高,但该算法的模态混叠端点效应易产生误差信号.针对上述问题,本文拟通过遗传算法(genetic algorithm,GA)确定VMD模数,提出一种基于VMD和双向长短期记忆网络(bi-directional long short-term memory,BiLSTM)的新型风电功率预测模型,以期获得更高精度的风电功率预测效果.
1 GA-VMD-BiLSTM预测模型
1.1 变分模态分解
VMD是一种以维纳滤波为基础,基于变分约束模型的非递归分解方法,构造变分模型并求取模型的最优解,再将复杂多分量信号分解成K个有意义的模态函数[8].具体实现步骤如下:
1) 建立变分模型.将原始信号f(t)分解成K个分量,各分量具有中心频率的有限带宽,用Hilbert变换解调解析信号,然后将信号平移到基带并混合中心频率估计信号带宽,使得各模态的估计带宽之和最小并保证各个分量之和与原始信号相同.构造变分函数模型
(1)
其中uk和ωk分别为分解后第k个模态分量和中心频率,∂t为时间t的偏导数,δ(t)为狄拉克函数,j为虚数单位,uk(t)为模态函数.
2) 求解变分模型最优解.引入拉格朗日乘数法算子λ(t),拉格朗日参数λ和二次惩罚参数α,将式(1)转化为增广拉格朗日函数
(2)
经迭代计算,得到第K个模态分量
(3)

通过以上建模和迭代计算过程,完成原始信号的变分模态分解.
1.2 遗传算法优化参数
为得到最佳分解效果,将遗传算法与VMD技术相结合,求取目标函数最优解,以此获得最优分解个数和惩罚因子[9].将VMD重构过程定义为函数
fvmd(SN[n],K,α)={uk|k=1,2,…,K},
(4)

(5)
本文利用VMD算法将风电功率数据分解成多个子函数,子函数作为模型输入,Loss值越小,分解损失越小,子函数中包含的信息越多,预测结果越精确.因此,采用遗传算法求取最优分解个数.设置参数优化模型,定义遗传算法适应度函数
(6)
(7)
通过遗传算法中的交叉和变异过程,选取自适应策略并计算适应度,确定最优分解个数和惩罚因子,分解原始信号,输入预测模型.
遗传算法参数设置和计算步骤如下:1) 设置种群个体数为8,最大迭代次数为20;2) 根据适应度,采用竞标赛法选择个体;3) 选中个体通过交叉和变异操作产生后代;4) 计算后代的适应度;5) 合并后代和上一代的个体,并根据适应度进行排序;6) 如果迭代次数大于20或10次迭代的最佳适应度保持不变,则结束算法.否则,重复步骤2)~6).
1.3 双向长短期记忆神经网络
Hochreiter和Schmidhuber提出的长短期记忆(long short-term memory,LSTM)是循环神经网络(recurrent neural network,RNN)的高级版本[10],不仅具有RNN对先前信息长期记忆的特点,而且将RNN中的循环隐藏层替换为“记忆块”,避免了RNN梯度消失的问题.LSTM的计算步骤如下:1) 计算遗忘门ft=σ(Wf·[ht-1,xt]+bf);2) 计算输入门it=σ(Wi·[ht-1,xt]+bi);3) 更新细胞状态Ct=ft×Ct-1+it×C′t;4) 计算输出门Ot=σ(Wo[ht-1,xt-1]+bo).其中σ为sigmoid激活函数;Wf,Wi,Wo分别为遗忘门、输入门、输出门sigmoid激活函数的权重;bf,bi,bo分别为遗忘门、输入门、输出门sigmoid激活函数的偏置;xt和xt-1分别为t和t-1时刻的记忆激活值;ht-1为t-1时刻细胞输出的激活函数;Ct和C′t分别为新细胞状态和细胞记忆状态.

图1 BiLSTM神经网络结构图Fig.1 Structure diagram of BiLSTM neural network
双向长短期记忆(bi-directional long short-term memory,BiLSTM)是LSTM的变形结构,包含前向和后向LSTM层,同时考虑数据的过去和未来信息[11],神经网络结构如图1所示.由图1可知,每个内存块包含两个LSTM层,输入各时刻时间序列X1,X2,…,Xt,通过前向LSTM层和后向LSTM层得到两个时间序列相反的隐藏层状态h1,h2,…,ht和h′1,h′2,…,h′t,然后将两个隐藏层状态连接起来得到相同的输出y1,y2,…,yt,前向LSTM和后向LSTM层可以分别获取输入序列的过去信息和未来信息[12].
1.4 预测模型
将VMD算法和BiLSTM神经网络相结合,利用GA算法自适应获取最优分解个数,改进VMD算法的分解过程,提出GA-VMD-BiLSTM预测模型,模型结构如图2所示.由图2可知,GA-VMD-BiLSTM预测模型主要分为数据处理、预测模型建立和预测结果计算三部分.首先,运用密度峰值聚类(clustering by fast search and find of density peaks,CFSFDP)算法进行数据清洗,将清洗后的数据集作为变分模态分解的输入;其次,建立BiLSTM神经网络预测模型,将分解后的数据IMF1,IMF2,…,IMFk-1,IMFk作为BiLSTM神经网络预测和训练的输入BiLSTM1,BiLSTM2,…,BiLSTMk-1,BiLSTMk,各BiLSTM神经网络相应输出Output1,Output2,…,Outputk-1,Outputk;最后,根据叠加合成结果n,计算得出模型预测结果.
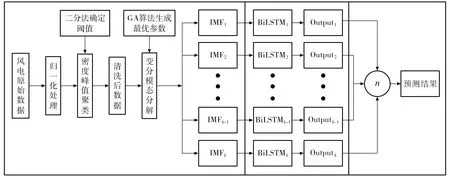
图2 GA-VMD-BiLSTM预测模型结构Fig.2 GA-VMD-BiLSTM prediction model structure
2 算例分析
2.1 数据处理
本文选取土耳其某风电场2018年实测数据作为原始数据集,采样间隔为10 min,共52 560组数据,随机选取1 000组数据进行处理,其中包括500组训练集数据和500组验证集数据.为了加速风电数据预处理和深度学习中模型收敛,须对风速、风向和功率等变量进行归一化处理,其转换公式为x′=(x-xmin)/(xmax-xmin),其中x和x′分别为原始数据和处理后的数据,xmin和xmax分别为原始数据的最小值和最大值.
本文提出一种改进参数获取的密度峰值聚类算法,通过改进参数指标的获取方法提高聚类性能,采用二分法得到密度计算的阈值dc,每个数据点周围距离小于dc的点数须占总点数的1%~2%,数据聚类效果如图3所示.由图3可知,数据集共有5个聚类中心,将数据分为5个簇,其中离群点1和离群点2的数据偏移量较大,须剔除.图4为数据清洗后的效果.由图4可知,偏离较大的数据均被清除,表明该算法的数据清洗效果较好.

图3 三维样本空间中数据和异常值的分布Fig.3 Distribution of data and outliers in 3D sample space
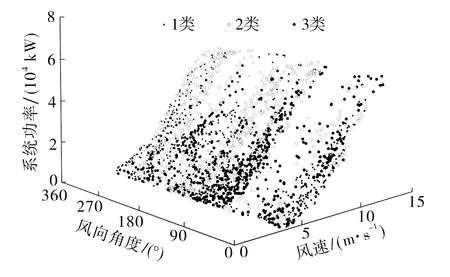
图4 数据清洗后样本空间中的数据分布Fig.4 Data distribution in sample space after data cleaning
2.2 结果与分析

图5 适应度函数曲线Fig.5 Fitness function curve
将归一化和聚类去噪处理后的原始数据集作为VMD算法的输入,通过GA算法自适应获取最优分解个数K的取值范围.图5为GA-VMD-BiLSTM预测模型的适应度函数曲线.由图5可知,GA-VMD-BiLSTM模型在第9次迭代时达到最优.设定K值为1~9,将不同K值下分解后的数据导入BiLSTM模型,得出预测结果B1,B2,…,B9,如图6所示.由图6可知,当K值为1~5时,预测结果逐渐趋于稳定;当K值为6~9时,预测结果波动逐渐增大.综上得出,当K值为5时BiLSTM模型性能最佳.
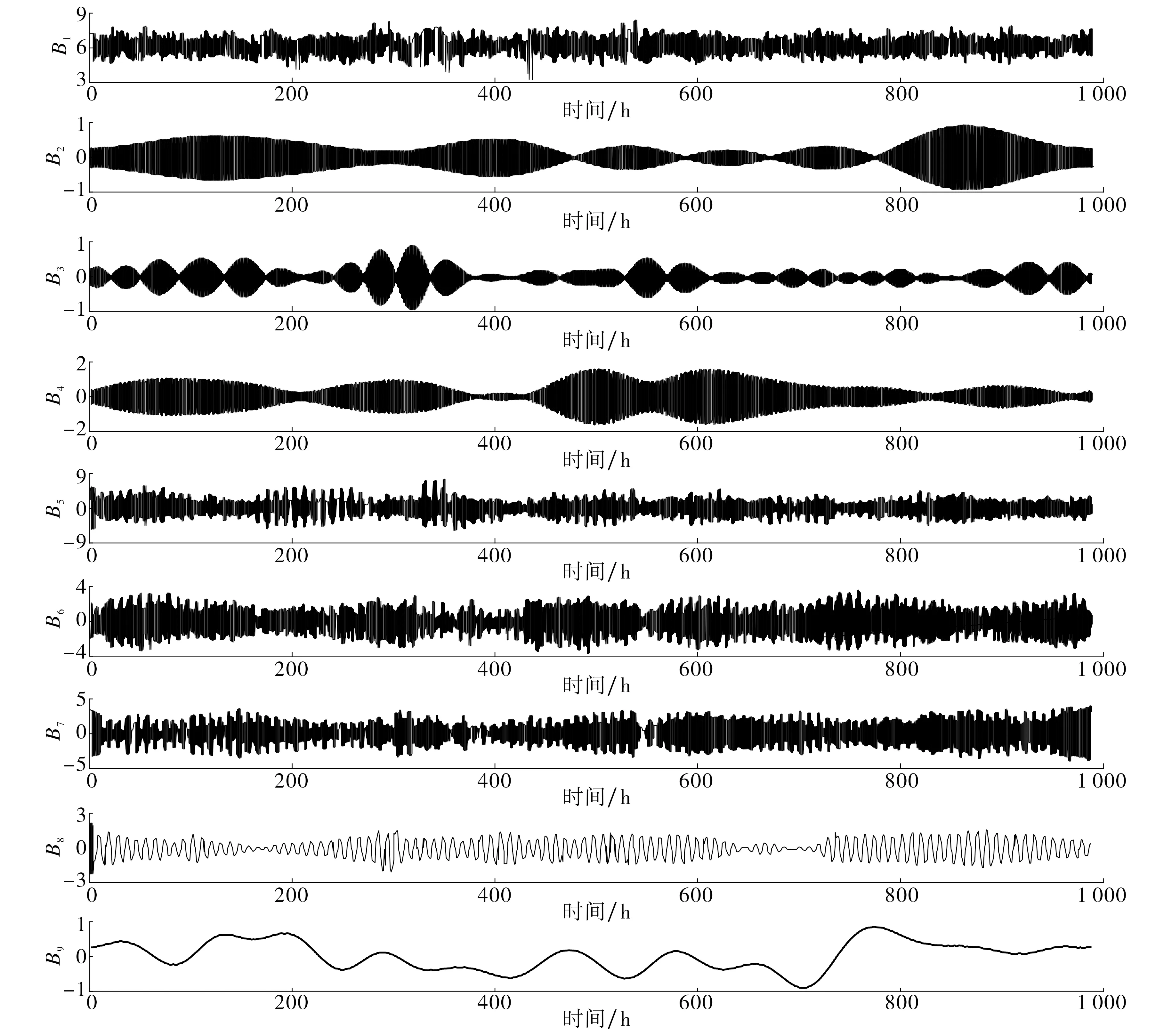
图6 VMD分解结果图Fig.6 VMD decomposition result

图7 各模型的预测结果Fig.7 The prediction result of each model
将原数据集分解为5个子数据集,分别建立基于BiLSTM,LSTM,极限学习机ELM和BP神经网络的预测模型,对比GA-VMD算法优化处理后的数据在各模型中的预测效果,结果如图7和表1所示.由图7可知,风电功率数据突变处,BiLSTM模型预测值与真实值吻合度较高,表明BiLSTM预测模型在极端情况下的适应能力较强,具有较好的鲁棒性和适应性.由表1可知,BiLSTM模型的均方根误差和平均绝对误差分别为0.156 97和0.349 64,相对于其他模型而言,预测结果误差较小,预测性能更优.综上得出,优化后的BiLSTM预测模型可有效处理风电功率时间序列数据,提高风电功率预测精度,并具有良好的泛化性能.

表1 各模型预测结果评价Tab.1 Evaluation of prediction result of each model
3 结论
为提高风电功率预测精度,保证风电并网的稳定性,本文提出了一种基于GA-VMD-BiLSTM的风电功率预测模型.采用密度峰值聚类算法去除无效数据点,改进截止距离dc的获取方法,降低数据维数和结果误差;利用遗传算法自适应选取参数,优化变分模态分解算法,并以BiLSTM为基础建立风电功率预测模型.测试结果表明,改进的BiLSTM预测模型相较于常用的LSTM,ELM,BP神经网络模型而言,提高了风电功率预测的精度和效率,具有更好的预测效果.
