基于浅水波方程的充排水过程模拟研究
2022-12-08王志良徐立洲丁志宏
王志良,徐立洲,丁志宏
(中水北方勘测设计研究有限责任公司,天津 300222)
修建输水系统是实现区域间水资源均衡配置、解决供需水矛盾的重要手段。近年来,我国建设了多项长距离引水工程,有效促进了我国社会经济发展。与此同时,大量关于引水系统充排水过程的研究被逐步开展。长距离管道输水过程是涉及明满流交替和气液两相流[1]的变化过程,杨开林等[2]提出了模拟无压隧洞充水过渡过程的“虚拟流动法”,求解了万家寨引黄入晋工程洞内初始无水条件下的充水问题。杨敏等[3]基于圣维南方程、假想窄缝法和虚拟流量法,建立了长距离串联输水管线的连续充水数学模型,并应用于南水北调天津干线有压系统充水模拟。王克忠等[4]采用Fluent软件对长距离无压引水洞岔洞的水力特性进行了模拟分析。
基于有限体积法和二维浅水波方程,搭建了二维水动力数学模型,对无压输水系统的充排水过程进行了数值仿真分析,研究成果可为复杂城市输水系统及长距离引水工程充排水过程的研究提供参考。
1 数值模型
1.1 数学模型
模型控制方程是服从静水压力分布假设的二维浅水波方程,这是描述非恒定渐变流的基本微分方程,其向量形式如下:
式中:h为水位(m);u为x方向流速(m/s);v为y方向流速(m/s);g为重力加速度(m/s2);Sox和Soy分别为x方向和y方向的地形坡度;z为地形高程(m);Sfx和Sfy分别为x方向和y方向的摩擦力,本文暂不考虑。
1.2 数值方法
有限体积法是将计算域划分为若干控制体,通过计算进出控制体边界的通量,基于质量和动量守恒定律,得到时段末各控制体上的物理量分布[5]。该方法物理意义明确,具有较好的守恒性,拟采用该方法结合Rusanov格式求解浅水波方程。计算域被划分为形状规则的矩形网格,首先将方程(1)离散并在控制体内积分,x和y方向的空间步长分别为Δx和Δy,时间步长为Δt,离散方程为:
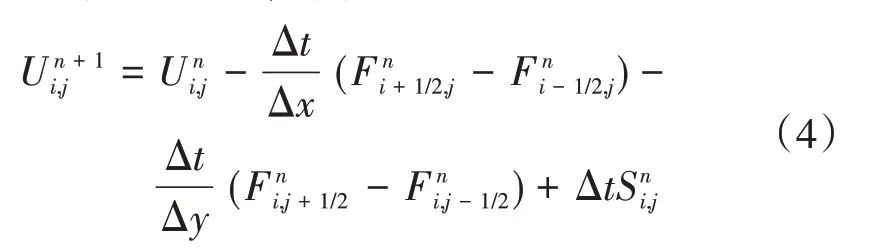
式中:i和j分别代表某一控制体在x和y方向的节点中心坐标;n代表某一时刻。
有限体积法的核心是构造边界通量,Rusanov格式的具体形式为:
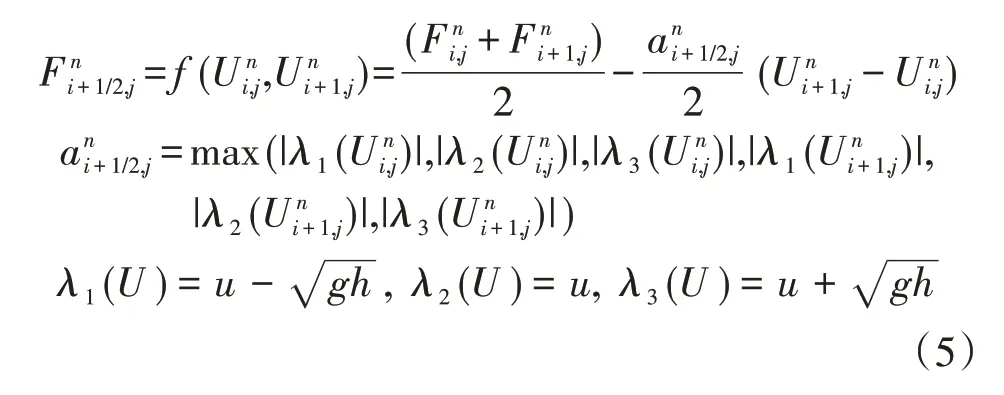
式中:λ1、λ2、λ3为方程(1)的Jacobi矩阵的特征值。
2 模型验证
2.1 理想地形静止算例
该算例中计算域的长和宽均为25 m,空间步长Δx=Δy=0.25 m,时间步长Δt=0.125 s,模拟时长为100 s,初始条件和地形方程为:

在无出入流条件下,计算域内应始终保持静止。计算时段末的水位分布和流速分布分别如图1和图2所示,可以看出,计算时段末整个计算域水面仍保持在0.1 m,且保持静止,即数值结果可很好地保持稳态,与实际情况相符。

图1 水位分布

图2 流速分布
2.2 干床溃坝算例
为了准确模拟输水系统的充排水过程,数值模型需具备处理干湿界面的能力,该模型中设计水位小于10-6m时,即为干河床。干床溃坝算例的计算域长度为10 m,宽度为1 m,空间步长Δx=Δy=0.05 m,时间步长Δt=0.02 s,模拟时长为6 s。坝体位于x=5 m处,初始条件和地形方程为:
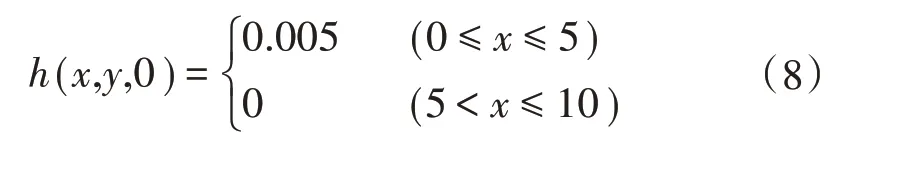

y方向上的物理量变化率为0,计算时段末x方向的水位分布和流速分布分别如图3和图4所示,可以看出,溃坝发生后,落水波传播至上游,上游水位下降,涨水波传播至下游,下游水位上升,且溃坝波未传播到的区域仍保持开始状态。特别地,下游落水波未传播到的区域可保持干床状态,这表明该模型可有效处理干湿界面。为了说明该模型的数值计算精度,将数值解与精确解进行对比,可以看出,计算水位与精确解误差较小,而计算流速除下游间断处外误差较小。
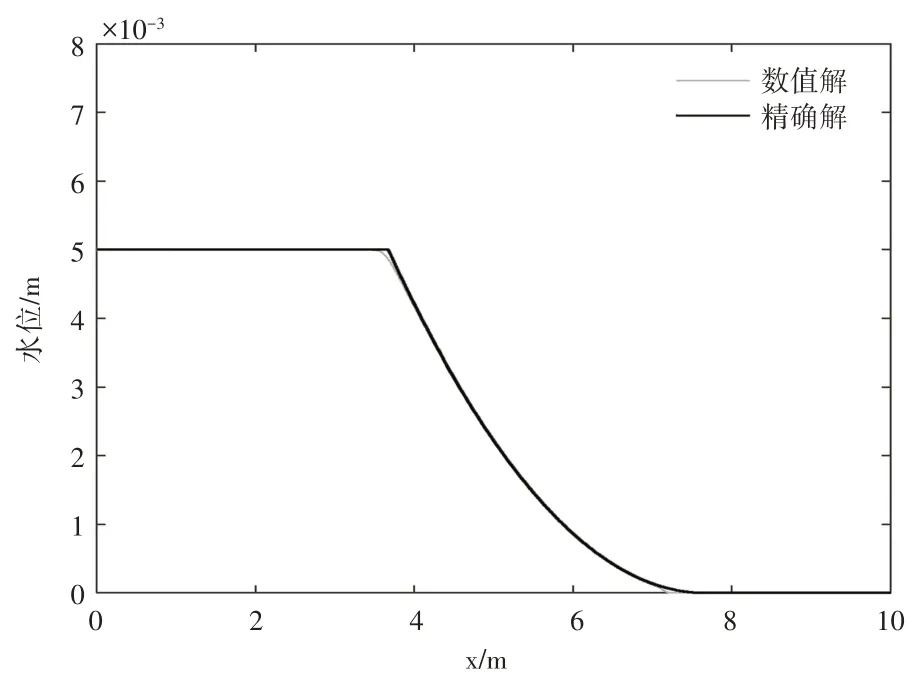
图3 水位分布

图4 流速分布
使用误差计算公式(10)-(11)进行计算,得到h和u的计算误差分别为0.004和0.1045,满足计算要求。

式中:eu和eh分别代表流速和水位的计算误差;unumi,j和分别代表(i,j)处的控制体的流速的数值解和精确解;和分别代表(i,j)处的控制体的水位的数值解和精确解。
3 数值实验
3.1 单向排水过程模拟
该算例上游入口为Wall边界,下游出流为20 m3/s,计算域长度为2000 m,宽度为30 m,系统坡度为0.001%,空间步长Δx=Δy=2 m,时间步长Δt=0.05 s,初始条件和地形为:
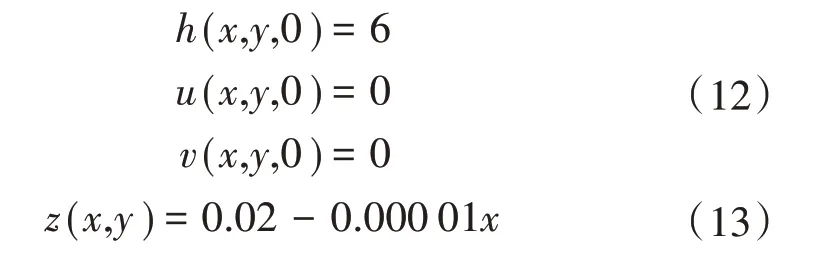
排水100、1800、3600 s时的水位分布和流速分布如图5和图6所示,可以看出,排水前期落水波逐渐向上游传播,出口处流速最大,上游水位为6 m,且保持静止;排水后期水面线为直线,越往下游流速越大。由图5和图6可知,出流100 s后,落水波传播至距入口1183 m处,出口处流速为5.6 m/s;排水1800 s后,系统水位自入口0.57 m降为出口0.41 m,出口处流速为2.12 m/s;排水3600 s后,系统水位自入口0.19 m降为出口0.14 m,且出口流速为1.28 m/s。
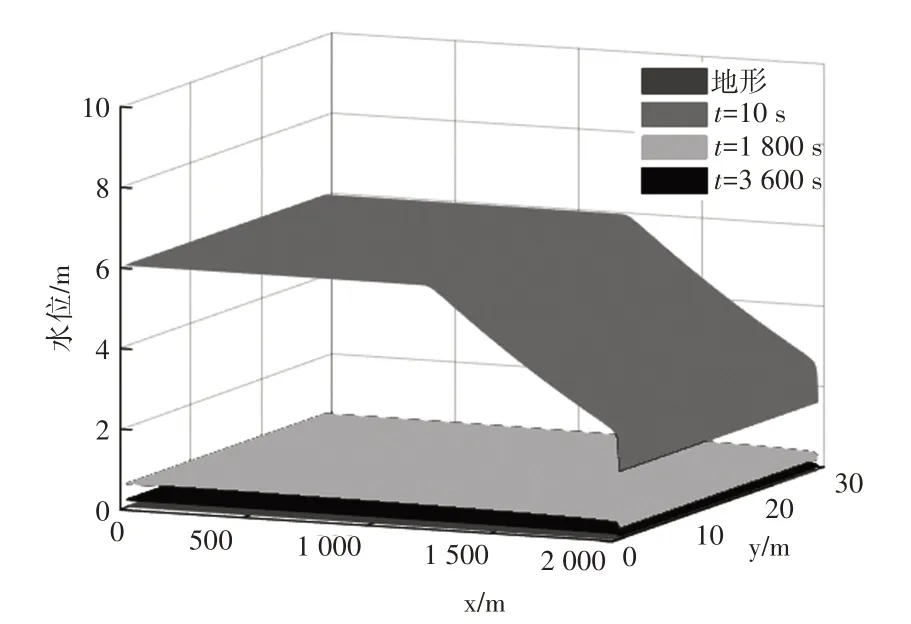
图5 水位分布
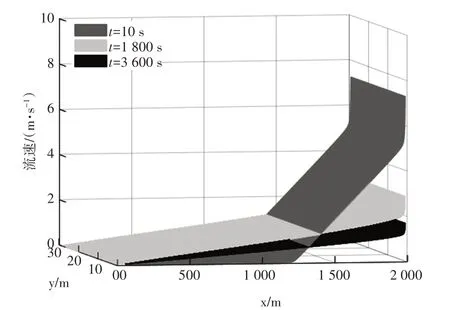
图6 流速分布
3.2 双向充水过程模拟
该算例为双向同时充水问题,上、下游充水流量均为20 m3/s,计算域长度为2000 m,宽度30 m,坡度为0.001%,空间步长Δx=Δy=2 m,时间步长Δt=0.05 s,初始条件和地形为:

充水1800 s和3600 s时的水位分布和流速分布如图7和图8所示,可以看出,上下游同时充水过程中,涨水波由系统两端向内部传播,汇合处水位最高,流速最小。由图7和图8可知,充水1800 s后,汇合段长162 m,水位0.03 m,汇合段上、下游侧流速分别为3.15、3.12 m/s;充水3600 s后,汇合段长356 m,水位为0.04 m,汇合段上、下游侧流速仍分别为3.15、3.12 m/s。与汇合处相比,系统两端的水位波动较大。
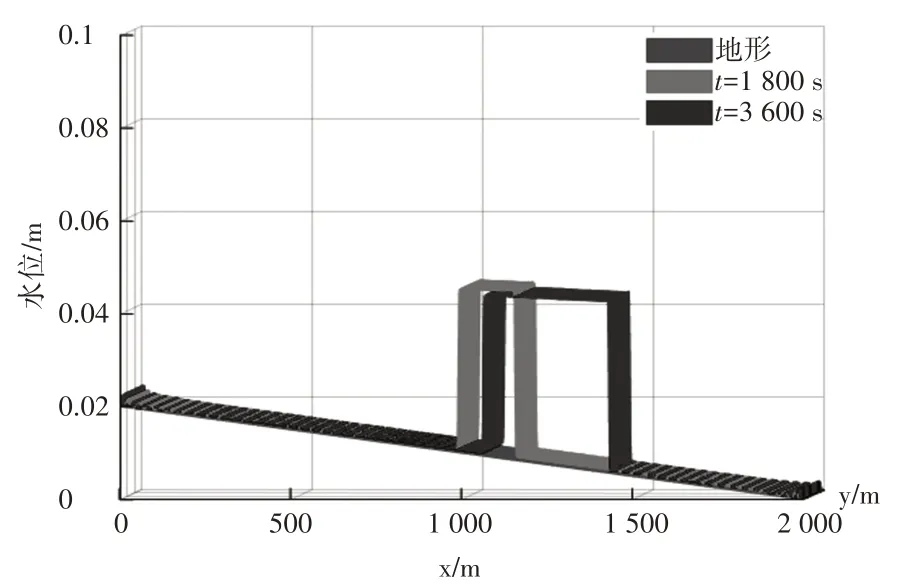
图7 水位分布

图8 流速分布
3.3 有障碍物的单向充水过程研究
输水系统的底面形状会影响水流的流态,以下算例模拟了有凸起的输水系统中的充水过程。入口边界施加水深0.7 m,出口为自由出流边界。计算域的长度为25 m,宽度为5 m,计算域内部有一圆锥形凸起,其中心位于(12 m,2.5 m)处,高度为1 m,其余区域平坦。空间步长Δx=Δy=2 m,时间步长Δt=0.05 s,模拟时长为6 s,初始条件为:

计算时段末的水位分布和流速分布如图9、图10和图11所示,可以看出,凸起前水位逐渐降落,凸起周围出现绕流现象,流态较为复杂。水流流至凸起处受到阻力而涌起,凸起上游侧及两侧水位骤升,水流的重力势能迅速转换为动能,流速增加。由图10和图11可知,4 s时绕过凸起的两股水流在下游侧有合并的趋势,6 s时凸起前侧的流速增大,水流涌起区域扩展,且两股水流在下游侧合并。
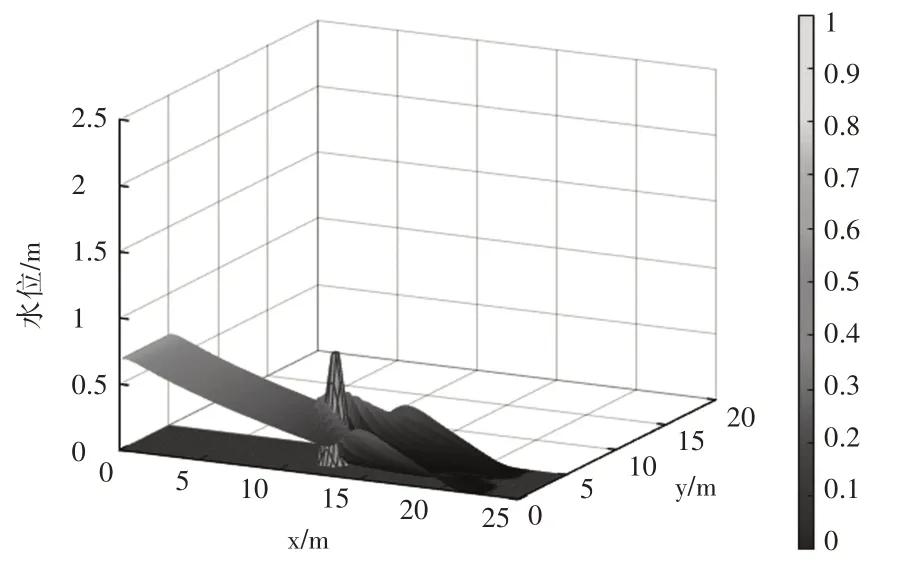
图9 水位分布(t=4 s)

图10 水位分布

图11 流速分布
4 结论
(1)基于浅水波方程搭建了二维水动力数值模型,采用有限体积法和Rosanov格式进行求解。静止算例验证了该模型可有效保持静水状态和适应复杂地形,干床溃坝算例验证了该模型可有效处理干湿界面,且计算精度较高。
(2)采用该模型模拟了具有坡度的输水系统中的单向排水过程和双向充水过程,不同时刻的水位、流速分布可反映出输水系统中的落水波和涨水波传播规律;采用该模型模拟了具有凸起的输水系统中的充水过程,模拟结果较好地反映出了障碍物周围的绕流现象,均符合实际物理过程。
实际输水系统的布置较为复杂,系统的形状、糙率及出入流状态都会影响水流流态。因此,后期需进一步在模型中考虑摩擦,并结合实际工程开展数值研究。
