泥石流拦挡坝有效坝高及坝后淤积计算模型探讨

黄金燕，张金霞，刘兴荣，马兴华，吴庆安，时 岩

(1.甘肃农业大学水利水电工程学院 甘肃 兰州；2.甘肃省科学院地质自然灾害防治研究所 甘肃 兰州)

泥石流是我国山区最主要的自然灾害之一[1- 2]，具有暴发突然、流速快、能量大、冲刷淤积明显、破坏力极强等特点[3- 4]，而拦挡坝又是当前减轻泥石流灾害最主要的手段之一[5]。

拦挡坝的科学布设在治理规划中直接关联着泥石流防治的成效，尤其是其坝后淤积直接反应流域防治的效益，长期以来，受到国内外许多科技工作者的高度重视。前人采用现场调查法[6]、室内模拟实验法[7- 8]、统计分析法[9]、实测法[10]等手段对各种拦挡坝的坝后淤积特征进行了广泛的研究，并建立了一系列拦挡坝有效坝高和坝后淤积坡度的计算模型。然而，由于泥石流物质组成和动态特征极其复杂、影响因素众多，尽管这些复杂的计算模型有其理论上的合理性，但其局限性也显而易见。此外，建立模型的基础数据往往来自于相应区域的泥石流实例，导致其地域性强，造成使用受限。因此，对泥石流拦挡坝有效坝高及坝后淤积计算方法进行梳理迫在眉睫。

泥石流拦挡坝有效坝高和坝后淤积坡度的设定是表征泥石流坝后淤积特征最为重要的指标，也是泥石流防治工程设计的关键参数。本文旨在归纳和总结国内外相关文献的基础上，通过梳理泥石流拦挡坝有效坝高和坝后淤积坡度的各种计算方法，比较其优缺点，以方便设计研究人员选择使用。

1 泥石流拦挡坝有效坝高计算

在进行拦挡坝工程设计时，有效坝高的计算是一项很重要的设计参数，直接决定拦挡坝在泥石流沟道中拦截泥沙的数量[11- 12]。在工程运用中可以按实际情况确定有效坝高，如按使用期多年累积淤积库容确定或按预防一次或多次典型泥石流的泥沙量确定有效坝高。

1.1 泥石流拦挡坝室内模拟研究

拦挡坝的库容受泥石流沟道纵坡、宽度、沟床粗糙率系数及有效坝高等因素的控制。李峰[13]、吴鑫[14]等通过模型试验初步揭示泥石流拦挡坝坝后淤积规律，认为有效坝高与回淤坡度呈二次函数关系，当沟床纵比降一定时，坝后回淤坡度随有效坝高呈先增大后减小趋势；崔佳慧[15]以粘性泥石流为例选取泥石流在不同沟床坡度条件下，通过室内模拟试验得到拦挡坝的坝高与回淤坡度呈负相关关系；而假设当沟床坡度为13°时拦挡坝的坝高和沟床坡度二者拟合相关关系为式(1)所示：

ik=9.26-0.29H

(1)

式中，ik—回淤坡度，H—有效坝高，θd—沟床坡度。

此外，王喜安[16]用KDEAY方法与前人野外考察数据结合，推导出拦挡坝有效坝高度对回淤比降折减系数K、下游侵蚀深度系数E、淤满程度系数D的影响，其表达式为公式(2)：

(2)

式中，Y—回淤压脚系数，反应泥石流拦挡坝有效坝高、坝间距设计是否合理及上游坝淤埋严重程度；Hb—回淤压脚高度；Hu—上游坝坝趾距溢流口高度。

以上研究主要为实验室模拟结果，尽管缺乏现场泥石流淤积特征检验，但为下一步建立野外拦挡坝坝后有效淤积提供理论支撑和方法依据。

1.2 泥石流拦挡坝有效坝高计算模型梳理

在工程设计中，为了计算方便，一般都采用经验公式，而将经验公式无差别地应用容易造成过度治理(造成浪费)或者不满足治理要求(达不到治理目的)，为了科学设定泥石流拦挡坝有效坝高，使库容计算更进一步精细化，学者们建立了不同地区、不同适用范围的泥石流拦挡坝有效坝高计算公式，见表1。

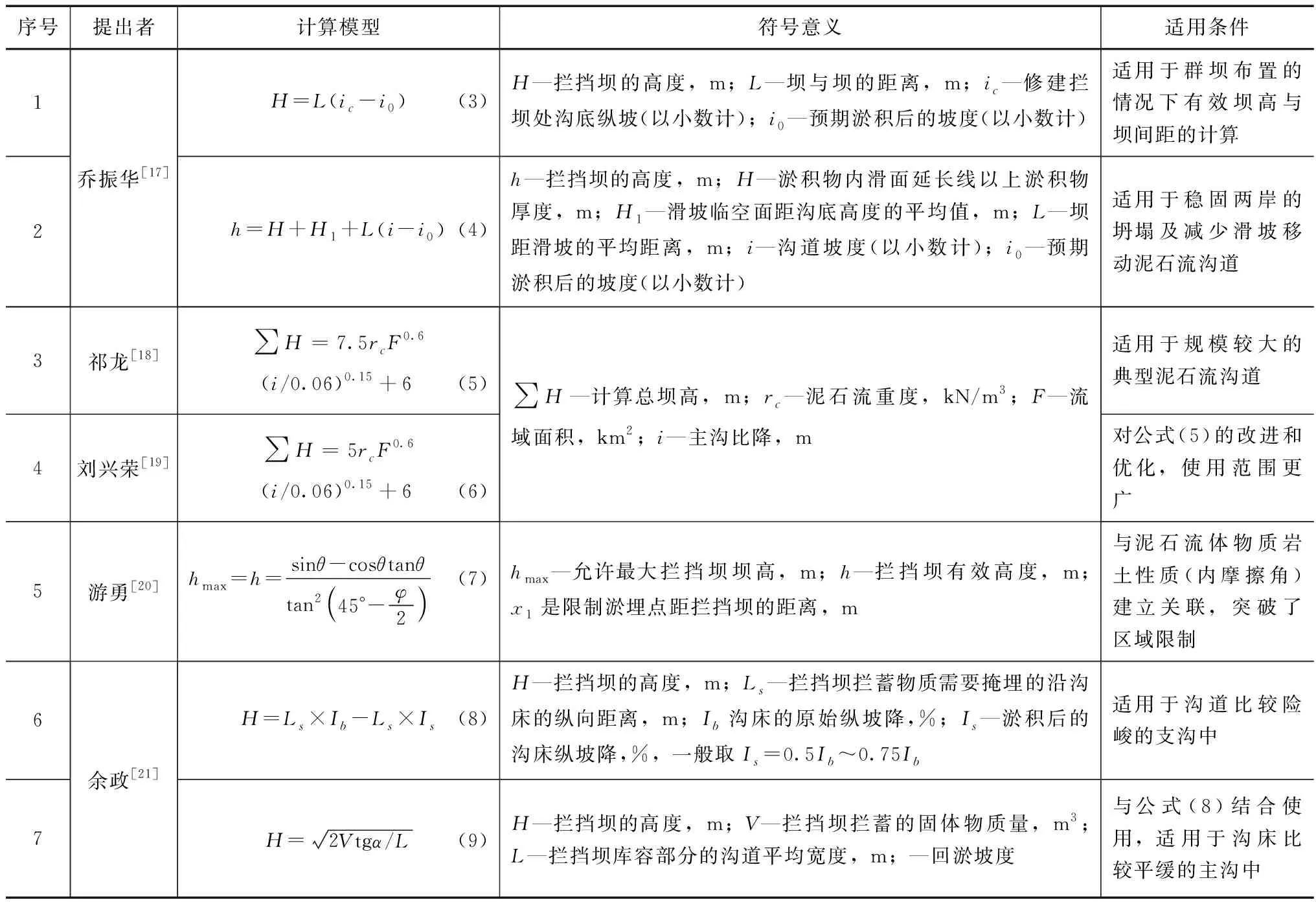
表1 泥石流拦挡坝有效坝高计算公式

表中，公式(3)和公式(4)形式简单，应用方便。公式(3)适用于拦挡坝群坝有效坝高与坝间距的计算，可用于设定拦挡坝坝群间距及数量；公式(4)适用于稳定沟岸两侧坍塌、滑坡的有效坝高度设定；对于公式(3)和公式(4)的使用要根据修建拦挡坝的目的，并结合地形条件后选择使用。公式(5)和公式(6)是以野外调查数据为基础，采用统计学方法对各项工程进行了治理效果评价，提出了拦挡坝布设总有效坝高的观点，认为拦挡坝修建并非越多越好，将拦挡坝的数量和总坝高控制在合理范围内，推动了泥石流防治向更科学和更合理的方向发展；公式(7)是假定坝后泥石流淤积厚度等于零时，确定库内不同位置处拦挡坝的允许最大有效坝高等工程设计参数；公式(8)和公式(9)则主要考虑了拟拦蓄的固体物质数量，又兼顾了拦挡坝稳固沟床的功能，按支沟和主沟分别进行讨论，使相关计算更精细化。

综上所述，拦挡坝有效坝高应根据实际所需，结合坝址及库区的地形、地质条件等因素后确定。

2 泥石流拦挡坝坝后淤积坡度计算

拦挡坝坝后淤积坡度是稳固上游沟床、岸坡和计算拦挡坝库容的一个重要参数[22]，不仅影响拦挡坝的拦截库容和工程效益，而且关系拦挡工程的预期效果和使用价值，对拦挡坝自身的抗冲蚀性及人民群众生命财产安全保护的有效性有着举足轻重的作用[23]。

2.1 坝后淤积坡度经验公式研究

目前对泥石流淤积坡度的计算研究仍处于室内溜槽模拟试验或野外调查获得定性的结论或经验判断阶段。见表2，汇总了国内外常用的泥石流坝后淤积坡度估算经验公式，并对其适用范围进行讨论。

表2 泥石流坝后淤积坡度计算公式

由表2知，公式(10)计算坝后回淤纵坡线，将回淤纵坡线、沟道线和拦挡坝合围的三角形横断面面积与沟道宽度的乘积可用于拦挡坝拦蓄库容的计算；公式(11)从泥石流坝后回淤坡度的机理出发，将坝后淤积与水动力条件建立关联，并采用实地调查案例对本回淤坡度的研究成果进行验证，其所得结果误差较小；公式(12)通过试验，采用河沟道平均比降的计算方法，建立了坝后淤积体的坡度与长度的函数关系；公式(13)利用Origin软件对回淤坡度ik沟床坡度θd与坝高H进行了线性拟合，建立了三者的线性相关关系；公式(14)知，在坝高一定的情况下，建立了库容与回淤坡度的动态关系。这类公式虽然能够确定拦挡坝的坝后回淤坡度，且计算简单、便于应用。但存在一定的区域局限性，导致计算结果差较大。

2.2 坝后淤积坡度计算模型梳理

泥石流拦挡坝坝后淤积坡度的研究，一般基于野外调查的类比分析或室内水槽的模拟实验进行。如国外学者Fleishman[27]、YUAN Dong等[6]通过理论分析和模型试验对坝后泥石流的回淤纵坡和透过型拦挡坝与实体坝回淤机理的差异作了定量的分析与研究，建立了坝后回淤厚度和纵坡的理论计算方法，但由于公式中的弗劳德数不易确定，因此较难在实际中推广应用；M.J.Bovis[28]通过简单的野外统计，得到回淤坡度随坝高增大而减小，随沟床纵比降增大而增大的结论，但并没有从机理上解释回淤坡度的影响因素，该结论为之后的研究提供了一些参考依据。国内学者依据回淤坡度、沟床坡度和有效坝高等相关关系，结合现场调查数据，修正模拟系数，进而较为精准地研究拦挡坝后回淤坡度变化规律，如吴积善[29]、余斌[30]等通过野外实验对泥石流坝后回淤规律进行归纳总结，并研究了不同容重下泥石流淤积厚度的计算方法；李峰[13]通过模型实验得到回淤坡度与沟床纵比降呈正相关关系，与坝高呈二次函数关系，即在一定坝高范围内，回淤坡度在随坝高的增大先增大后减小；赵静静等[15]通过水槽模拟试验，研究黏性泥石流的坝后回淤坡度，认为坝后回淤坡度与沟床坡度和有效坝高三者之间呈线性相关，且沟床坡度和拦挡坝高等都会影响拦挡坝坝后泥石流的回淤坡度；吴鑫[14]、吴积善[29]通过模拟试验，认为粘性泥石流的回淤坡度在底坡坡度的0.76～0.85范围内，相同坝高情况下，粘性泥石流的回淤坡度较稀性泥石流略大，而回淤坡度随沟床纵坡增大而增大，二者呈线性正相关关系；祁龙等[18]在对云南大桥河、蒋家沟等泥石流沟进行实地观测的基础上，研究了回淤坡度与沟床比降的关系，但仅仅给出了大致的比降变化范围，未进行相关的定量研究；韩文兵[31]以水石流为研究对象，研究了梳子坝与具有相同切口宽度的实体坝的对比试验，试验结果表明，切口密度对回淤坡度有一定影响，同时证明原沟床坡度、物质级配、容重及规模对回淤坡度也有一定影响。

总之，学者们进行了许多野外统计和室内实验，总结出了一些定性的结论，揭示了拦挡坝坝后泥石流淤积规律，提出了许多估算坝后淤积坡度的经验和半经验公式，为后续的研究提供了一些参考。

3 结论

通过对泥石流拦挡坝有效坝高及坝后淤积关键参数计算的汇总和比较，得出以下结论：由于泥石流在行进中伴随着复杂的水土动力过程，致使拦挡坝有效坝高及坝后淤积计算方法复杂多变；定性或者定量的经验公式，存在一定的区域局限性；为方便计算而随意设定拦挡坝有效坝高及坝后淤积计算模型，容易造成浪费甚至不满足防护要求的极端情况。

今后，随着科学技术和探测手段的提升，应不断修正和细化模型参数，同时将有效坝高和坝后淤积作为一个整体来考虑，建立更为精确且通用的计算模型。