基于气象因子的土壤含水量模拟研究

王 慧，李靖瑄，刘小妮，沈丽娟，吴晓文，鲁素芬

(1.山东省水文中心，山东 济南 250000；2.昆明理工大学津桥学院建筑工程学院，云南 昆明 650106；3.河海大学水文水资源与水利工程科学国家重点实验室，江苏 南京 210098)

土壤含水量是农业和畜牧业等领域衡量土壤干旱水平的重要指标[1]，对作物生长与区域生态建设具有重要的影响。由于土壤水的特殊性，在实际应用中土壤水分测定需要投入大量的人力物力，而且土壤水时空变化的复杂性使得监测难度加大，因此，对土壤水含量进行合理有效的数值模拟及预报有着重要的理论及实际意义[2- 3]。目前，关于土壤水含水量的模拟模型种类繁多，遵循原理各异，主要分为物理性模型和随机性模型[4- 5]。郝振纯等[6]研究了2003—2012年山西省土壤含水量的时空变化规律，仅探讨了降水和气温2个气象因子对土壤含水量变化的影响；侍永乐等[7]基于多元线性回归与BP神经网络方法建立了土壤相对湿度预测模型，发现降水、气温、日照时数、风速、相对湿度、蒸发量等气象因子与土壤相对湿度存在相关关系；张祥星等[8]应用数理统计方法研究发现气象因子与不同深度的土壤含水量相关系数年内变化较大，表明不同深度的土层含水量存在一定的差异性。土壤水分的变化在不考虑人工管理(灌溉、翻耕)条件下，主要是由降水、气温、风速、湿度、日照时数等气象要素的变化引起的[9- 10]。以往研究表明，土壤水分变化与降水、气温等气象因子存在强烈的耦合关系[11]。因此，对土壤含水量的模拟及预报实质上是基于气象因子对土壤水分变化的综合影响进行模拟[12- 13]。

本文以山西省为研究区域，构建基于降水、气温、日照时数、风速、相对湿度等多气象因子的多元线性回归、BP神经网络和多元非线性回归3种随机性模型，对山西省10、20、40cm土壤含水量进行模拟分析。因此本文构建的模型可以为该地区合理安排灌溉提供科学依据，具有一定的实用价值。

1 研究区域及数据来源

1.1 研究区域

山西总体地势轮廓呈“两山夹一川”形势，东西两侧是山地和丘陵，中部自东北至西南走向为串珠式沉陷盆地和平原[14](如图1所示)。境内地形地貌十分复杂，山地、丘陵、高原、盆地等均有分布，大部分地区海拔在1500m以上。土壤类型主要为棕壤。全省降水受地形影响很大，山区较多，盆地较少。日照充足，热量资源较丰富，但灾害性天气较多，“十年九旱”[15]。

图1 山西省土壤墒情与气象站点分布图

1.2 数据来源

本文采用的土壤含水量资料与气象资料来源于1970—2012年山西省7个土壤墒情监测站及其邻近气象站的观测数据，各墒情站与气象站详细信息见表1。土壤墒情监测站观测期为每年的3—11月份，土壤含水量采用烘干法测定，取样深度分别为10、20、40cm 3个层次，取样时间为每月的1、11、21日，每层的月平均值分别取本月各测次的算术平均，各测点的土壤含水量平均值按3点取样法计算[16]。本文模拟计算采用的土壤含水量为旬值，降水为旬和，气温、日照时数、风速和相对湿度为旬平均值。

表1 山西省墒情站与气象站信息表

2 研究方法

本文基于降水、气温、日照时数、风速、相对湿度、土壤含水量等变量，构建了3种随机模型：多元线性回归模型、BP神经网络模型和多元非线性回归模型[17]。根据模型输入要素的不同，多元非线性回归模型分为A、B、C 3种类型，各模型输入输出要素见表2，并采用相关系数和相对误差作为3种模型评价指标。

表2 3种随机模型及其输入要素表

3 结果分析

3.1 多元线性回归模型分析结果

多元线性回归是确定2种或2种以上变量间相互依赖的定量关系的一种统计分析方法。由于其结构简单，易于操作，被广泛应用于社会、经济、技术及众多自然科学领域的研究中[18]，如张敬超等[19]基于多元线性回归模型分析了内蒙古东北部鄂温克族自治旗1990—2017年土壤含水量的动态变化与气候因子之间的相关关系。山西省面积较大，地形地势多变，针对山西省不同地区不同土壤深度的土壤含水量建立基于气象因子的多元线性回归方程，模拟土壤含水量与气候要素的线性关系。根据土壤墒情站与气象站的实测资料，计算得到7个墒情站点的多元线性回归方程，见表3。

表3 多元线性回归模型对各层土壤含水量的模拟及评价

由表3可知，相关系数均通过了显著性检验，10cm土层含水量的拟合效果较好，其次是20cm土层，40cm土层拟合效果最差，这是因为表层土壤水受气象因素的影响大，而深层土壤水受到的影响较小。但相对误差<20%的所占比例并不高，其中，界河铺、义棠和柴庄站的相对误差小于20%的比例比较低，均小于54%，3个站点分别位于山西土壤含水量较低的忻定盆地、太原盆地和临汾盆地；油房站相对误差小于20%的比例稍高，该站位于南部沁河流域；长子和榆社站相对误差小于20%的比例较高，长子站位于土壤含水量整体较高的长治盆地，榆社在长治盆地北侧。说明该模型在土壤含水量比较少的地区适用性较差，在土壤含水量比较多的地区拟合效果较好。汾河二坝站模型的2项评价指标在各站中都是最差的，而其土壤含水量较高，土壤类型为沙土，其他6站为壤土，说明该模型在壤土地区的适用性要优于沙土。

3.2 BP神经网络模型分析结果

考虑到土壤墒情与气象因素的关系复杂，并不是单纯的线性关系，而BP神经网络可以通过自己学习和反复调整训练，使模型的输出结果与期望输出结果的误差满足一定要求[20]，故选择BP神经网络进行模拟。其具体结果见表4。

表4 BP神经网络模型对各层土壤含水量的模拟及评价

由表4可知，BP神经网络模型模拟的10cm土层含水量的拟合效果较好，这与多元线性回归模型模拟结果一致，通过对比相关系数与相对误差2项评价指标，可知BP神经网络模型在山西省的应用效果略优于多元线性回归模型，与李柳阳等[21]研究结果基本一致，说明土壤含水量与某些气象因子存在非线性的关系。

3.3 多元非线性回归模型分析结果

由前文可知，在输入变量不引入前期土壤水的情况下，BP神经网络模型与多元线性回归模型模拟的效果并不理想，不能很好的用于实践，考虑到土壤含水量与某些气象因子存在非线性的关系，所以尝试应用非线性回归方法[22]，同时引入前期土壤水作为自变量，对土壤含水量进行滚动预报。这种方法既可以保证入选的自变量相互独立，又可解决自变量与因变量并非均为线性关系的问题。根据输入变量的不同，本文把多元非线性回归模型分为A、B、C 3类，模型要素见表2，计算得到的多元非线性回归方程见表5(为节约篇幅只给出模型B、C公式)，评价指标见表6。

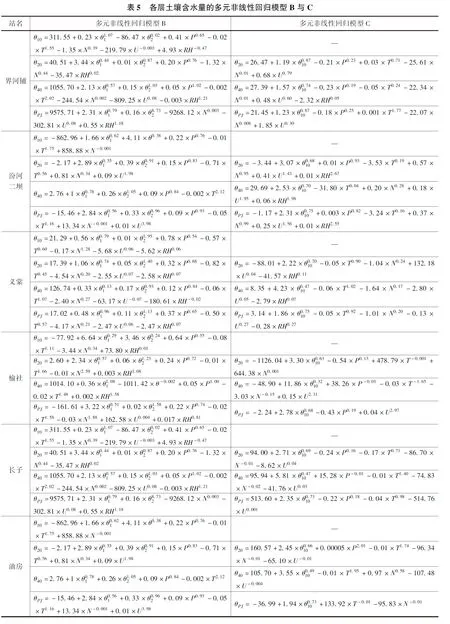
(续表)

由表6可知，模型B的精度高于模型A，其模拟的土壤水平均值效果最优，相关系数都大于0.7；均是榆社、长子和油房站的效果较好，另外4个墒情站次之。从相对误差来看，各站土壤水平均值模拟效果最优，10cm土层模拟效果最差。多数站点40cm土层模拟效果优于20cm土层。模型C引入10cm土层土壤水做自变量，结果发现评价指标均优于模型A、B；相关系数都大于0.88，相对误差小于20%的比例都大于80%。20cm土层的模拟效果很好，40cm土层的模拟效果一般.

表6 多元非线性回归模型A、B、C对各层土壤含水量的模拟评价

为进一步对比分析模型B、C对土壤含水量的模拟过程变化，本文选择20cm土层模拟效果较好的榆社、长子和汾河二坝站，土壤含水量变化过程线如图2所示。由图2可知，模型C模拟值的过程线要比模型B拟合的更好。榆社站模型C过程线整体上拟合的更好，有些点几乎和实测值重合，20cm模拟值中，有些最小值比实测值小。长子站模拟值与实测过程线几乎重合，20cm和平均值的相关系数分别为0.882和0.924，相对误差小于20%的比例分别为93.4%和95.9%。汾河二坝站虽然各项评价指标都有很明显的提升(见表6)，但从对比图看出，模型C在有些年份波动太大，拟合较模型B差，比如2000、2001和2002年。在2003、2004和2012年拟合明显比模型B好。(为节约篇幅，只给出部分过程线图)榆社站43年土壤含水量均值为15.3%，与邻近气象站的距离最近，在各个模型的应用中，其相关系数一直是最优的站点，相对误差小于20%的比例仅次于长子站。长子站土壤水均值为19.1%，在7个站点中含水量最高，且各层含水量常年相对稳定，其相对误差最优，相关系数仅次于榆社站。汾河二坝站土壤水均值为16.9%，但从图2(c)可知，土壤水年内波动较大，土壤类型为沙土，不利于土壤水的保持。界河铺站土壤水均值为11.3%，在7个站点中含水量最少。汾河二坝站用多元线性回归模型和BP神经网络模型效果最不好，其次为界河铺站。在引入前期土壤水后，汾河二坝的模拟效果提高，界河铺为最不好站点。

图2 土壤含水量变化过程线

与多元线性回归模型和BP神经网络模型2种模型相比，同一墒情站点，多元非线性回归模型引入前期土壤水为自变量后，模拟精度明显提高，尤其是20cm土层和40cm土层提高幅度更明显，且各项评价指标优于10cm土层。多元非线性回归模型在长治盆地和沁河流域等土壤含水量高的地区，模拟效果比较好，在忻定盆地、太原盆地和临汾盆地等土壤水较少的地区，模拟效果略差。这与前两种模型结论基本一致。且土壤类型对模型的模拟效果也有一定影响，含水量相差不多的情况下，3种模型对土壤类型为壤土的站点模拟效果要优于沙土站点。即汾河二坝站为沙土，土壤含水量又比较高，其他几个均为壤土，含水量多数低于汾河二坝，但汾河二坝的模拟效果相对比较差。

4 讨论

通过改变各模型的输入要素，不断改进多元线性回归模型、BP神经网络模型和多元非线性回归模型，虽然模拟精度显著提高，但仍存在一些问题。本文就气象资料与模型本身对模拟精度的影响进行讨论分析。

(1)气象资料。站点位置的迁移对气象要素的影响很大，邻近气象站降水量很大，墒情站的降水有可能比较小，甚至为0；两类站点有可能出现风向完全相反等情况。因此移用邻近气象站的气象资料是模型误差的一个很重要的原因。

(2)墒情站资料。墒情站点的具体情况缺少记载，比如观测前是否有灌溉，如果有灌溉，且无降水时，观测值肯定要大于模拟值；站点43年中下垫面是否有变化，植被的有无直接影响土壤含水量的变化。这些都可以导致相对误差小于20%的百分比降低。

(3)输入变量。多元线性回归模型和BP神经网络模型输入变量只有气象要素，缺少前期土壤水这一重要影响因子。一定程度降低了模型应用效果。

(4)随机模型的局限性。随机性模型中的参数一般没有具体的物理意义，不能反映出土壤水与影响因素之间的物理关系，而要想得到更加准确的预报，必须同时考虑其它动态影响因素的作用，这是此类模型主要的局限性，必然导致模拟精度不可能很高。

5 结论

本文基于气象因子构建了多元线性回归模型、BP神经网络模型和多元非线性回归模型，通过构建不同输入要素的土壤含水量模型，以此提高多元非线性回归模型对山西省土壤含水量的模拟能力。同一随机性模型在山西省各个站点的应用情况不一，不同模型的应用效果分布规律一致。结论如下：

(1)3种模型中多元非线性回归模型模拟精度较高，各项评价指标明显增加，模拟与实测值的过程线拟合的也比较好。模型引入前一旬土壤水与前一、两旬土壤水均引入的模拟效果差异不大，且前一、两旬土壤水均引入后略优。BP神经网络模型的模拟效果略优于多元线性回归模型，两者对10cm土层拟合较好。

(2)3种模型模拟结果均表现为土壤含水量高的站点模拟的效果要优于土壤含水量偏低的站点，且土壤类型为壤土的站点模拟效果要优于土壤类型为沙土的站点。

(3)根据历史土壤水和气象资料建立多元非线性回归模型，本文以10cm土层土壤水作为因子之一，采用滚动预报对20、40cm土层的土壤水进行模拟预报，模拟结果较好，可为土壤水资料同化提供一种新的借鉴，在仅观测地表土壤水的地区可以模拟预报下层土壤水变化。