基于优化算法的组合模型在水库年径流预测中的应用

祖 佳

(辽宁省朝阳水文局，辽宁 朝阳 122000)

在水文科学领域内，中长期径流预测的准确性一直是热点和难题。近年来，中长期径流预测的模型和方法取得一定研究成果[1- 8]，但在实际应用中存在精度不高的问题[9]。目前，提高中长期径流预测精度的重要手段是对单一模型进行改进或者建立不同模型的组合[10]。相比于单一改进模型，组合模型可综合考虑不同模型计算的优点，通过设置权重系数进行模型组合，在一些区域中应用效果好于单一中长期径流预测模型[11- 15]，但总体还是难以达到理想的误差精度。当前，许多模型通过进行参数优化使计算精度得到提高，许多参数优化算法通过样本数据系列，以模型计算误差为目标函数，对模型的参数进行不断优化和调整，将模型预测精度提高。SMA算法由于具有较快的收敛度和较强的搜索能力，近年来在优化算法函数中脱颖而出。

辽西地区属于辽宁省典型的干旱半干旱区，中长期径流预测精度对水库调蓄规划十分关键。为提高辽西地区水库中长期径流预测精度，本文组合国内中长期预测效果较好的灰色模型与BP神经网络模型，并结合SMA算法对其参数进行优化，以区域内2座大型水库白石水库和阎王鼻子水库为实例，进行模型精度验证和对比。研究成果对于水库中长期径流预测方法具有参考价值。

1 组合模型构建及优化算法

1.1 组合模型构建

本文将灰色模型和BP神经网络模型进行组合，由于模型在国内应用较为成熟，对其模型原理不再叙述。组合模型的原理在于可将不同模型通过组合权重进行组合，综合利用不同模型的优点进行分析。灰色模型对短期预测具有较高的精度，但是对长期波动性较大的数据预测精度不高；BP神经网络模型对数据系列非线性变化特征较强，能够较好地模拟，但其收敛速率较低，且在局部由于训练时间较长容易出现极小值。因此将灰色模型和BP神经网络模型进行组合，可综合不同模型之间的优势。组合模型预测的最关键要素是合理确定组合权系数，本文以最小绝对误差为目标函数进行组合模型的建立。

(1)

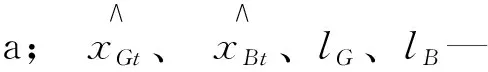
(2)

式中，lk—不同组合模型的权重系数；di—预测时段内不同模型的残差平方之和。本文中组合模型的数量为2个，其权重系数计算方程分别为：

(3)

(4)

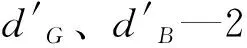
Pt+1=P0[P(1)]t+1

(5)

式中，Pt+1—t+1时刻的概率分布；P0—无条件概率初始时刻的分布；P(1)—概率转移矩阵，其计算方程为：

(6)

式中，pij—从tn时刻到tn+1时刻的概率转移值；m—转移变量的总数。

1.2 SVM优化算法原理

SVM优化算法通过不断逼近目标函数来实现参数的优化，其快速收敛的原因在于不同调整变量参数自适应的权重，其变量位置优化调整方程为：

(7)

其中：

p=tanh|s(i)-DF|，i=1，2，…，k

(8)

式中，ub、lb—目标搜索区间内的上限和下限值；rand—在[0，1]范围内随机数；参数vb的变化区间为[-a，a]；参数vc的变化区间为[0，1]且呈线性递减变化；t—迭代步长；x—目标搜素所在位置；xm、xn—2个随机选取的位置；w—搜索因子权重；s(i)—x的适应度；DF—在目标优化求解过程中的适应度最佳值。参数a的计算方程为：

(9)

式中，maxt—迭代最大次数。w权重值计算方程为：

(10)

其中：

smellindex=sort(s)

(11)

式中，r—在区间范围为[0，1]的随机数；bF—迭代过程中适应度最高值；wF—迭代过程中适应度最低值；smellindex—搜索过程中目标函数因子的适宜度系列。

2 实例应用

2.1 水库概况

本文以白石水库和阎王鼻子水库为具体实例，2座水库均为辽宁省朝阳市的大型供水水库。白石水库修建于1995年，坝址以上控制面积为17649km2，为大凌河干流主要控制型工程，水库总库容为16.45亿m3，多年入库水量均值为7.24亿m3。阎王鼻子水库修建于1996年，坝址以上控制面积为9482km2，总库容为2.17亿m3，多年入库水量均值为8.08亿m3。本文结合白石水库和阎王鼻子水库2000—2020年入库径流作为模型的样本数据系列，其中2000—2016年入库径流量数据系列作为训练样本，2017—2020年作为模型精度验证年份。

2.2 不同维度优化函数对比

不同维度SVM优化算法，其优化求解精度有所差异。为提高SVM优化算法对水库入库径流组合模型的优化求解精度，分别选取5种测试函数进行SVM优化算法不同维度下的仿真计算，其中SMA算法和PSO算法迭代次数最大值均为100次，种群规模和学习因子均为50和2.0。不同维度优化函数寻优求解能力对比结果见表1。

表1 不同维度下SMA算法和PSO算法的寻优对比结果

本文将不同优化算法下的最优值设置为0。从对比结果可知，不同维度条件下，SMA算法对于单峰函数而言其寻求求解精度好于PSO算法；而SMA算法对于2种多峰函数而言，其不同维度条件下经过40次寻优后可达到设理论最优值0。表明就寻优精度而言，SMA算法要好于PSO算法。此外对于多峰函数Ackley，由于该函数旋转不可分的特点，在各维度条件下SMA算法寻优精度逐步趋于稳定。综上，SMA算法由于具有较好的优化和极值搜索能力，其寻优结果好于PSO算法，将该算法用于组合预测模型可行。

2.3 模型参数设置

采用SMA算法分别对灰色模型与BP神经网络模型参数进行优化设置，其中灰色模型2个参数分别为发展系数α和内部控制变量b，BP神经网络模型2个参数分别为权值η和连接阈值θ。2个模型设置训练精度为0.001，最大训练步骤为10000次。模型参数优化结果见表2。

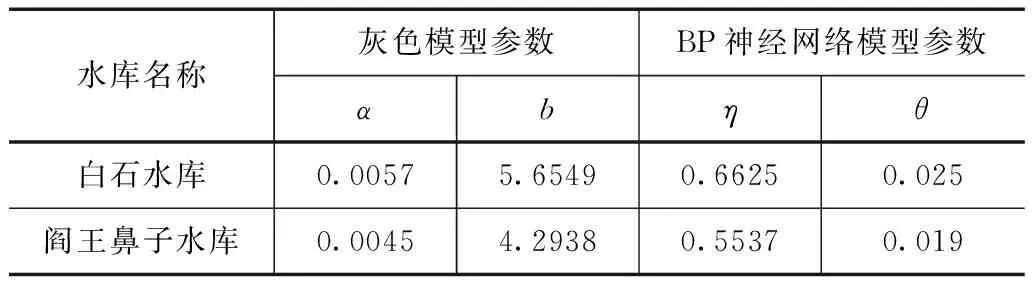
表2 模型优化参数结果

2.4 模型预测

结合模型参数优化结果进行灰色模型和BP神经网络模型参数设置，按照白石水库和阎王鼻子水库2000—2016年年入库径流数据作为训练样本进行误差绝对值分布计算，按照马尔科夫链模型进行不同预测区间的划分，其中白石水库的马尔科夫状态区间划分为：[0 15%]、(15% 25%]、(25% 35%]、(35% 65%]。阎王鼻子水库的马尔科夫状态区间划分为：[0 6%]、(6% 11%]、(11% 20%]、(20% 45%]。组合模型拟合误差系进行分类后对转移概率矩阵进行确定，分别为：

(11)

(12)

结合白石水库和阎王鼻子水库2000—2016年入库年径流数据，按照划分的状态区间对组合模型误差序列进行修正，并结合优化后的模型参数，利用2个水库状态转移概率矩阵代入方程(5)进行水库入库径流预测，预测结果见表3。

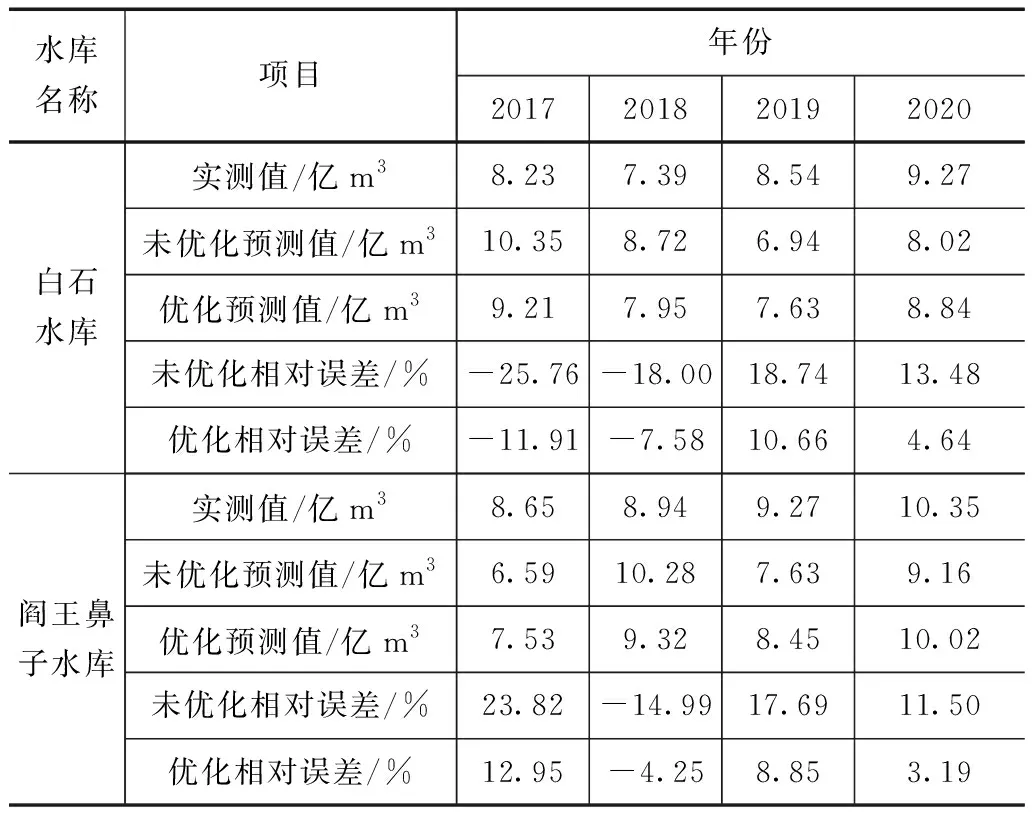
表3 优化参数的修正组合模型预测结果对比

从参数优化前后修正组合模型在2个水库入库年径流量预测对比结果可看出，参数优化后修正的组合模型预测精度明显好于参数优化前。白石水库参数优化前相比于优化后，其相对误差均值可降低10.3%；阎王鼻子水库参数优化前相比于优化后，其相对误差均值可降低9.69%。采用SVM算法对修正组合模型进行参数优化后，提高了组合模型寻优能力，加速了最优解收敛精度，从而提高了其模型预测的精度。从参数优化前2个水库采用修正组合模型的相对误差来看，相对误差在±20%以内，而进行优化后，相对误差均可在±15%以内。

3 不同模型精度对比

分别将参数优化前后的单一灰色模型、单一BP神经网络模型及参数优化前后的修正前后组合模型，对2017—2020年白石水库、阎王鼻子水库进行入库径流量预测，并统计其平均相对误差MAPE，取各年份预测相对误差绝对值的均值，均方根误差，并将预测相对误差±20%认为其预测结果在合理范围内，统计不同模型预测的合格率，结果见表4。

对比白石水库和阎王鼻子水库2017—2020年入库年径流量预测结果可知，相比于其他5种模型，参数优化后的修正组合模型(模型6)平均相对误差MAPE可降低约10%13%，均方根RMSE误差平均可降低约34%～42%。对于预测合格率而言，认为预测相对误差在±20%以内属于合格，从对比结果可看出，单一BP神经网络模型参数优化前后2个水库的预测合格率均可以达到50%，修正组合模型参数优化前后其预测合格率得到明显提升，参数优化后的修正组合模型其预测合格率可达到100%，预测合格率得到明显改善。

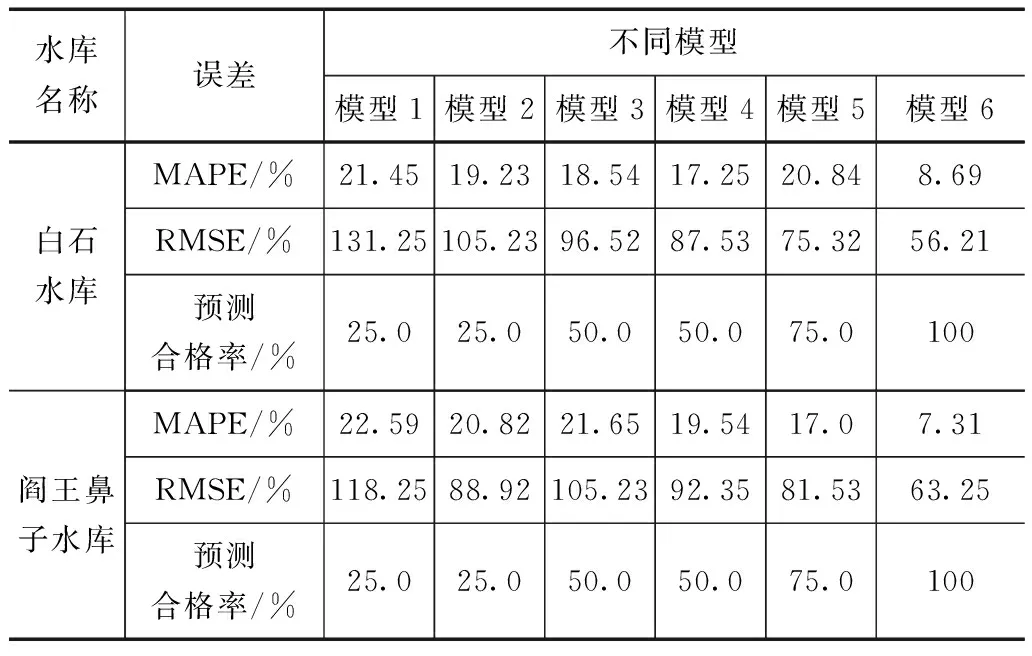
表4 不同模型预测精度对比

4 结论

(1)对于SMA黏菌优化算法而言，在多峰函数条件下相比于单峰函数，其各维度下寻优搜索能力都有所提升，不同维度条件下经过40次寻优后可达到设理论最优值。

(2)通过实例分析，采用马尔科夫链对组合模型进行修正后，能将组合模型结构进行优化，从而降低传统模型组合权重系数的不确定性对其预测精度的影响。

(3)本文预测及验证的样本数据系列较短，在后续的研究中，还需要将参数优化后的修正组合模型在不同区域进行长序列样本数据系列的验证应用，不断优化模型结构，扩大模型应用面。