假设检验方法在电极质量改进中的应用与研究

王登学，李爽，王小磊，孙敬哲

(蓝星(北京)化工机械有限公司，北京 100176)

1 假设检验方法概述

电极作为氯碱电解装置的核心部件，对电解槽的平稳运行起到关键性作用。在电极制作过程中，原材料、烧结温度、烧结时间等制作工艺参数以及涂布设备、烧结炉、烧付位置等都对电极性能产生重要影响。

在日常生产当中，我们经常面临比较分析的问题，例如，改进措施执行后质量是否提高，两条生产线生产的产品是否一致，两个批次产品之间是否存在差异，等等。这些可以归结为用样本观测值对总体的性质做出结论性判断的问题，如果依靠经验去判断，往往会得出错误的结论，而假设检验为我们提供了科学的统计方法。

对于这样的问题，先把某个结论当成假设，然后根据样本观测值，运用统计分析的方法对假设进行检验，并做出判断，这种方法称为假设检验。假设检验是采用逻辑上的反证法，利用小概率事件(P<0.05)在一次试验中几乎不会发生的思想，提出假设，再根据统计方法确定发生的可能性，以此判断假设是否成立。一般根据实际问题建立原假设H0和备择假设H1，选择合适的检验统计量，明确其分布，设定显著性水平α(当H0成立时，拒绝原假设的临界概率)，并计算P值(当H0成立时，抽取到当前样本的概率)，根据P值与显著性水平α之间的关系，来判断接受或者拒绝原假设。

假设检验方法应用范围非常广泛，主要包括均值检验、方差检验和比率检验等，如表1所示。双总体均值、方差检验的详细信息如表2所示。

表1 假设检验方法汇总

表2 两正态总体均值、方差的显著性水平为α的检验

本论文主要介绍双总体均值检验中的双样本T检验在电极寿命改进中的应用。

2 假设检验步骤

下面以双样本T检验方法为例，介绍假设检验的步骤。

两组样本数据，第一组数据的均值用1表示，第二组数据的均值用2表示。

①建立假设：H0∶μ1-μ2=0，H1∶μ1-μ2≠0。

②选择检验统计量，确定拒绝域的形式。

选择t统计量作为检验统计量：

③给出检验中的显著性水平α。

在对原假设是否成立进行判断时，由于样本的随机性，判断可能产生两类错误，见表3。第一类错误：H0为真时，拒绝原假设的错误，其发生的概率称为犯第一类错误的概率，记为α，即P(拒绝H0|H0成立)=α。第二类错误：H0为假时，做出无法拒绝原假设的错误，其发生的概率称为第二类错误的概率，记为β，即P(不拒绝H0|H1成立)=β。犯第一类错误的概率不能超过某个水平α，由此给出的检验称为“水平为α的显著性检验”，称为显著性水平，通常取为0.05。

表3 假设检验中的两类错误

④给出临界值，确定拒绝域。

⑤根据样本观察值，计算P值并进行判断。

通过计算出的t值，对照t分布的分位数表，可以得到对应的P值，如果P值小于α，拒绝原假设，证明两组数据存在显著性差异，反之，则不能拒绝原假设，两组数据无差异。如图1所示。

图1 α与P值的关系

3 双样本T检验在不同烧结炉产品分析中的应用

电极寿命是评价电极性能的主要指标，通过强化检测前后的质量差来表示。

在实际生产当中，不同批次产品的寿命波动很大，有时甚至遇到寿命不合格的情况，经过分析原因，初步判断问题可能来自于不同的烧结炉或者不同的涂布生产线。从生产现场收集145组生产数据，包含烧结炉、生产线、寿命等信息，如表4所示。

表4 生产数据表

对数据求均值，如表5所示。烧结炉1生产的电极寿命均值为4.68，烧结炉2的均值为5.79，二者相差1.11；涂布线1的均值为4.75，涂布线2的均值为5.02，二者相差0.27。烧结炉之间以及涂布线之间寿命都存在差异，只是烧结炉之间的差异更大，那么如何判定哪个是显著因子呢？由于生产时存在随机误差，两组数据之间必然会存在一些小的差异，如果是显著因子，两组数据之间的差异必然会很大，那么差异到底多大才是显著因子呢？双样本T检验给出了科学的统计方法。

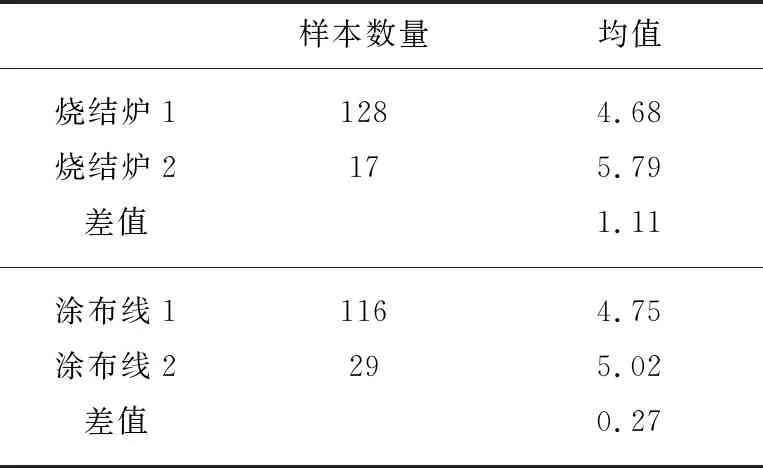
表5 数据汇总表

3.1 数据收集

首先验证数据的测量系统，Gage R&R以及P/T都全合格后再收集数据，如表3所示。

3.2 双样本T检验应用的前提条件

使用双样本T检验，必须满足以下3个条件。

(1)两组样本内部相互独立，两组间也相互独立。

(2)两组数据都来自正态分布总体。

(3)两个总体方差相等。

3.2.1 独立性检验

建立假设。

H0：数据是相互独立的；H1：数据不是相互独立的。

选取显著性水平=0.05，画出运行图，通过游程的数量计算相应的P值，如图2、图3所示。

关于中位数的游程个数：56；期望游程个数：64.8；关于中位数的游程最大长度：14；检验聚类性的近似P值：0.059；混合的近似P值：0.941；向上或向下的游程个数：82期望游程个数：85.0；向上或向下的游程最大长度：4；检验趋势性的近似P值：0.263；检验振动性的近似P值：0.737。

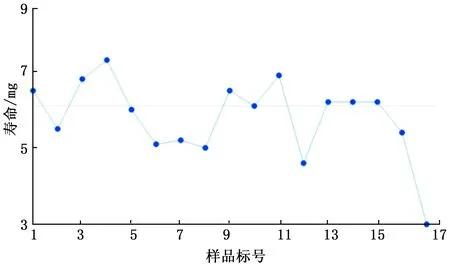
关于中位数的游程个数：10；期望游程个数：9.5；关于中位数的游程最大长度：4；检验聚类性的近似P值：0.605；混合的近似P值：0.395；向上或向下的游程个数：11；期望游程个数：11.0；向上或向下的游程最大长度：4；检验趋势性的近似P值：0.500；检验振动性的近似P值：0.500。

从图2可得：烧结炉1的独立性的P值为：聚类性的近似P值=0.059，混合的近似P值=0.941，趋势性的近似P值=0.263，振动性的P值=0.737。这些P值均大于0.05，不能拒绝原假设，因此说明，烧结炉1的数据是独立的。

同理，可以证明烧结炉2的数据也是独立的。

3.2.2 正态性检验

建立假设。

H0：数据服从正态分布；H1：数据不服从正态分布。

选取显著性水平α=0.05，画出正态概率图，并计算相应的P值，如图4、5所示。

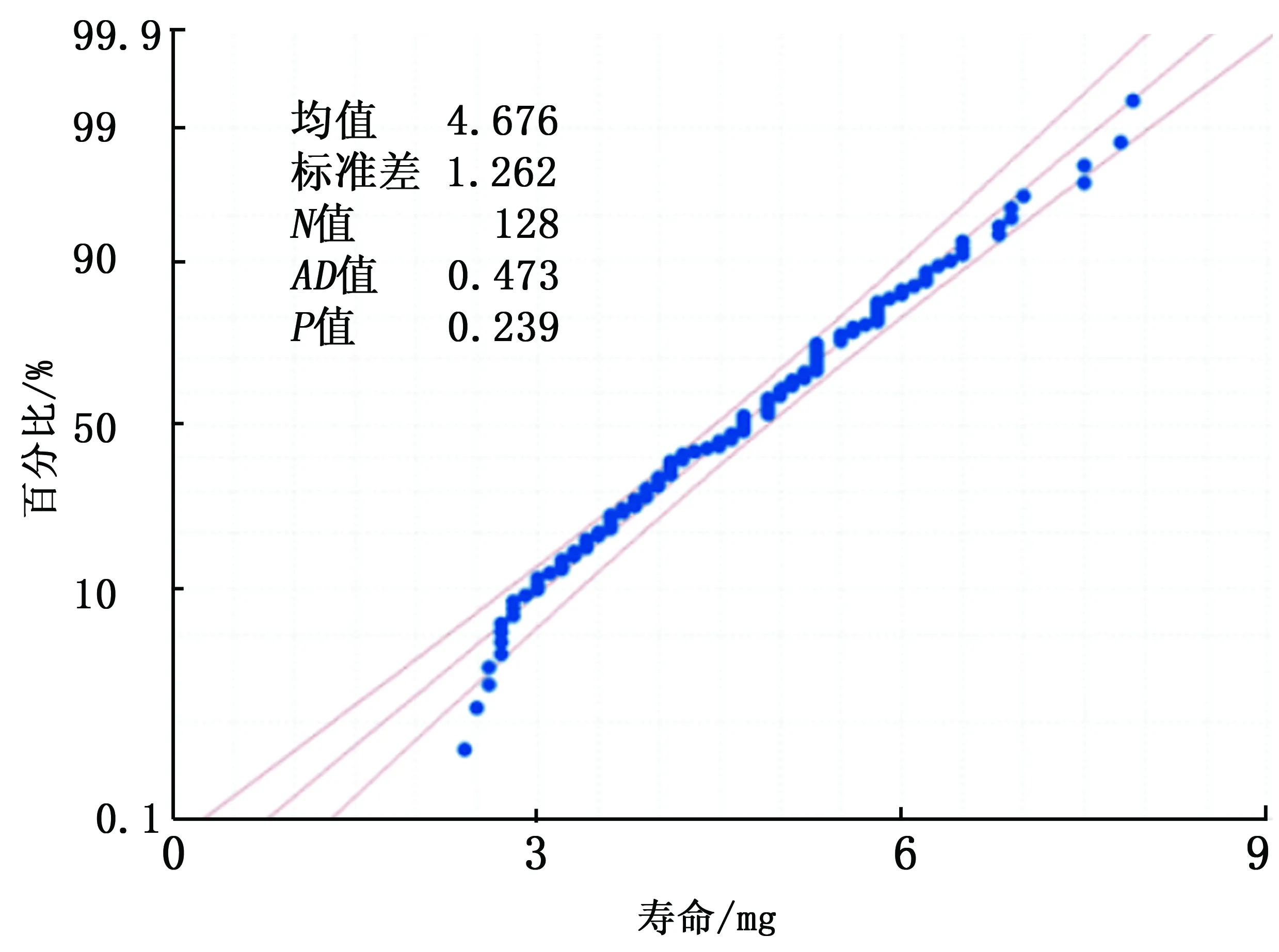
图4 烧结炉1的正态概率图

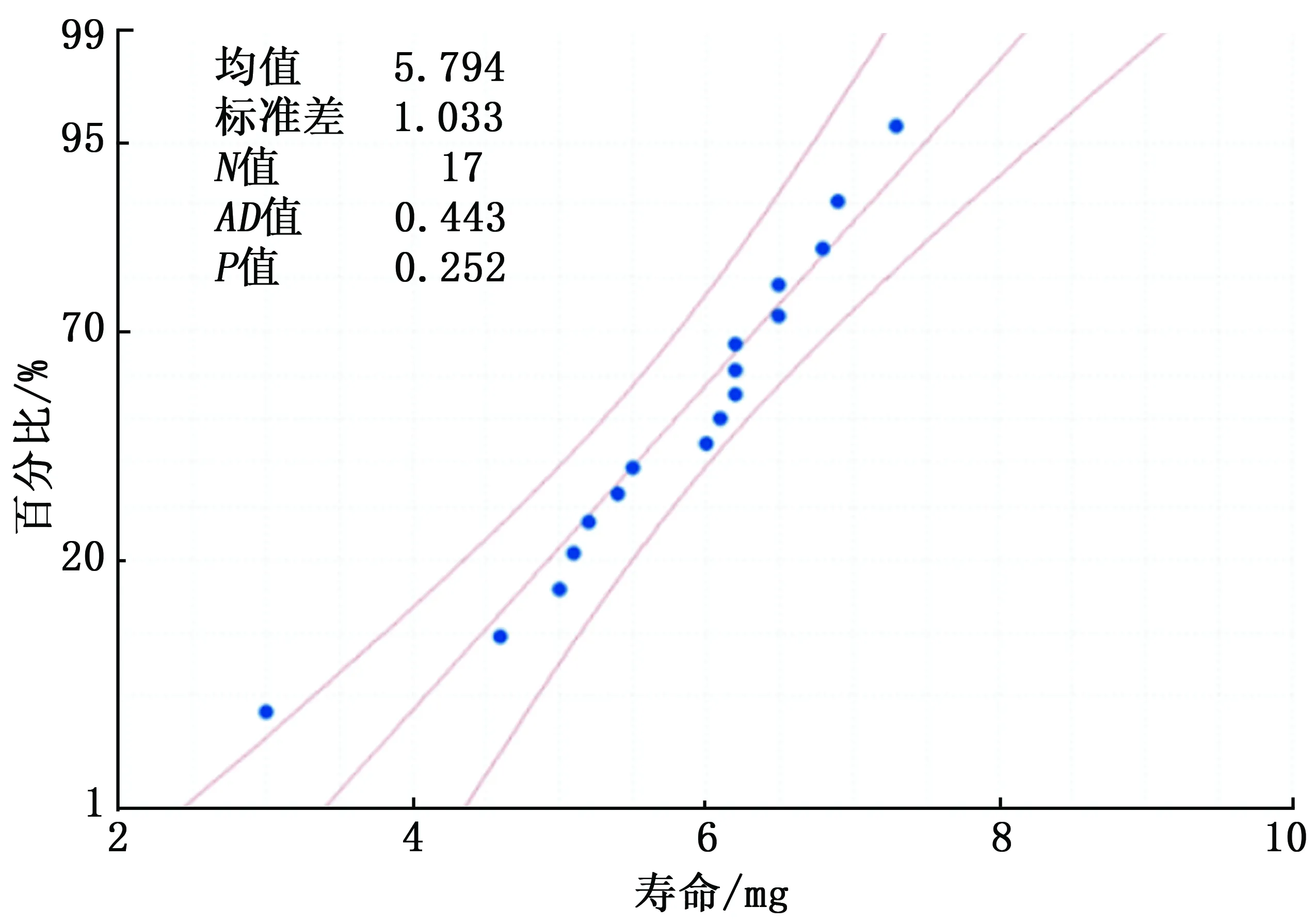
图5 烧结炉2的正态概率图

从图4、5可知：烧结炉1的P值=0.239，烧结炉2的P值=0.252，P值均大于0.05，不能拒绝原假设，因此说明，烧结炉1和2的数据都是正态的。

3.2.3 等方差检验

建立假设。

选取显著性水平α=0.05，画出寿命置信区间图，并计算P值，如图6所示。P值=0.336>0.05，说明，烧结炉1和2的数据是等方差。

图6 双方差检验置信区间图

3.3 双样本T检验

建立假设：

图7 两个烧结炉寿命的箱线图

表6 两个烧结炉寿命的双样本T检验和置信区间

差值=μ1-μ2；差值估计值：-1.118；差值的95%置信区间：(-1.687, -0.550)；差值=0 (与≠) 的T检验：T值=-4.08，P值=0.000，自由度=22。

3.4 结论和措施

从表6可得：P值=0.000<0.05，拒绝均值相等的原假设，证明，烧结炉1和2存在显著性差异。也就是说，烧结炉2是导致寿命偏高的主要变异源。

经过对烧结炉2的内部结构深入检测分析，我们发现烧结炉2的热电偶在测试位松动，导致烧结炉的烧结温度偏低，影响了电极寿命。

我们制作了防呆装置，把热电偶卡在固定位置，该问题得到彻底解决。

4 双样本T检验在不同涂布线产品分析中的应用

同样，我们收集不同涂布线生产的产品信息，如表3所示。

建立假设：

H0∶μ1=μ2；

H1∶μ1≠μ2。

先对数据的独立性、正态性和等方差检验，结果都满足3个前提条件。

双样本T检验的分析结果见表7和图8所示。

图8 2条涂布线寿命的箱线图

表7 2条涂布线寿命双样本T检验和置信区间

差值=μ1-μ2；差值估计值: -0.271；差值的 95%置信区间: (-0.798, 0.255)；差值=0(与≠)的T检验:T值=-1.04，P值=0.305，自由度=44。

结论：从表5可得，P值=0.305 > 0.05，无法拒绝均值相等的原假设，证明，涂布线1和2没有显著性差异。

5 结语

在实际生产当中，遇到的比较分析问题非常多，假设检验为我们提供了科学的统计方法，该方法的应用避免了人为的经验错误。

以假设检验为理论基础的方法很多，我们经常使用的包括双样本T检验、配对检验、F检验、卡方检验等，在使用这些方法时，应注意如下4个问题。

(1)收集数据的测量系统分析必须合格，即GageR&R%和P/T%，必须满足要求。

(2)每个假设检验方法使用前，都应满足其前提条件，否则不能使用。

(3)假设检验只是给出统计意义上的结论，是否正确还需要和实际情况进行对比验证。

(4)根据结论找到问题的根本原因，当措施实施之后，应再收集数据验证措施的效果。