入渗补给范围对包气带水气两相流运移过程影响的数值模拟研究

江训才，冯洪川，祝晓彬,2*，吴吉春,2，吴剑锋,2，熊贵耀

（1.南京大学 地球科学与工程学院，表生地球化学教育部重点实验室，南京 210023；2.自然资源部地裂缝地质灾害重点实验室，南京 210049）

入渗补给范围对包气带水气两相流运移过程影响的数值模拟研究

江训才1，冯洪川1，祝晓彬1,2*，吴吉春1,2，吴剑锋1,2，熊贵耀1

（1.南京大学 地球科学与工程学院，表生地球化学教育部重点实验室，南京 210023；2.自然资源部地裂缝地质灾害重点实验室，南京 210049）

【目的】基于数值模拟方法揭示入渗补给范围对包气带中水气两相流运移过程的影响。【方法】基于多相流数值模拟软件TOUGH2/EOS3构建水气两相流数值模型，模拟分析不同入渗补给范围对包气带中水分入渗补给过程的影响。【结果】研究表明存在临界入渗范围L0，大于和小于此临界入渗补给范围时，包气带中水分运移规律差异明显。在此基础上，进一步探讨了影响临界入渗范围的因素。数值模拟结果表明，毛管压力的变化对临界入渗范围的影响较大，不考虑毛管压力作用会使包气带中水分渗流在垂直方向更加集中，此时入渗范围对水分入渗的影响较小。【结论】在一定范围内，包气带厚度与临界入渗范围呈正相关，补给速率与临界入渗范围呈负相关。

包气带水分运移；临界入渗范围；TOUGH2/EOS3；水气两相流；数值模拟

0 引 言

【研究意义】灌溉水、降水通过包气带入渗补给饱和地下水的过程是水文循环和地下水污染过程中至关重要的环节之一[1]，由单相到多相的数值模拟技术是研究包气带中水分运移的重要手段[2]。包气带中的水分运移过程本质上是水气两相流迁移过程[3-7]，两相流条件下的水分迁移涉及较为复杂的理化转变过程[8-10]。【研究进展】关于入渗补给源对包气带中水分运移的影响，前人主要集中研究入渗强度、入渗时长以及入渗量等因素对包气带水分迁移影响[11-14]，而关于入渗补给范围对包气带水分运移影响的研究较少。Lai等[15]结合野外田间双环入渗试验并利用HYDRUS-2D模型进行包气带中水分运移的单相流模拟，探究双环入渗仪内环尺寸范围对土壤饱和渗透系数的影响；唐泽华等[16]通过染色示踪试验研究试验尺度对浅层土壤包气带中水分非均匀流的影响。【切入点】以往研究主要关注入渗补给范围对浅层土壤中水分迁移的单相流问题，但实际上浅层土壤包气带中的水流运移过程涉及水气两相流问题，灌溉水入渗补给过程即是水分在浅层土壤包气带中的迁移过程，深入研究入渗补给范围对包气带中水分运移有利于优化灌溉入渗补给方案，提高水资源利用效率。【拟解决的关键问题】鉴于此，本研究利用TOUGH2/EOS3构建水气两相流模型[17]，用数值模拟方法深入分析入渗补给范围对浅层土壤包气带中水气两相流运移的影响。研究结果一定程度上可丰富浅层土壤包气带中水分运移特征的理论基础。

1 材料与方法

1.1 模型概况与参数

根据典型地层剖面，同时结合主要研究目标，设置概念模型。模拟区域概化为垂向二维剖面，饱和带和包气带介质岩性均为粉砂，模型尺寸为80 m×40.5 m，将顶部0.5 m厚的薄层设置为大气边界层，地下水埋深为25 m，饱和带厚度为15 m，如图1（a）所示。模拟计算网格剖分如图1（b）所示，网格大小为1 m×1 m，顶部为固定大气压力边界（P0=1.013×105Pa），底部为固定压力边界（P1=2.484 5×105Pa），左右为零通量边界。

粉砂介质关键参数取值参考软件库相关参数以及Sun等[18]对包气带中水气两相流入渗补给的研究结果，如表1所示。在模型顶部中央区域设置入渗补给源，恒定补给速率q=2×10-5m/s，考虑设置不同入渗范围L=6、8、10、14、16、18、20、30 m等8种情况下的包气带水分运移过程。

图1 二维概念模型和入渗补给范围示意Fig.1 Two-dimensional concept model and schematic diagram of infiltration recharge range

表1 粉砂介质主要参数[18]Table 1 Main parameters of silty sand[18]

注λ为经验参数；Slr为多孔介质水相残余饱和度；Sls为多孔介质饱水时的水相最大饱和度；Sgr为残余气相饱和度；Pmax为最大吸力；1/P0为土壤进气值的倒数。

1.2 研究方法

基于多相流数值模拟软件TOUGH2/EOS3构建水气两相流数值模型，开展入渗补给范围对包气带水分入渗过程的影响研究。TOUGH2是国际上常用进行多相、多组分流体流动及热量运移的数值模拟软件[17]，该软件以其模块化的程序结构，公开的程序代码，通用的离散方法以及高效的求解方法等优点，在碳封存、核废料处置、污染修复、环境评价以及地热开发等领域有着广泛的应用。TOUGH2中包含多个不同状态方程（EOS）模块，不同EOS模块用于求解不同数学模型，其中EOS3模块可用于求解包气带中水气两相流的数学模型。

包气带中水气两相的运动均遵循质量守恒定律和能量守恒定律，水气两相流达西定律[19]为：

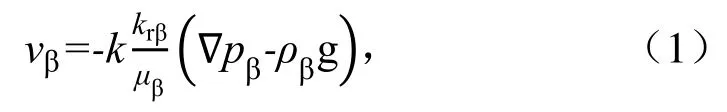
式中：vb为b相的渗透流速（m/d）；k为介质的绝对渗透率（m2）；krb为b相的相对渗透率（m2）；mb为b相的动力黏滞系数（Pa/s）；pb为b相的压力（Pa），rb为b相的密度（kg/m3）；g为重力加速度（m/s2）。

包气带中水气两相流运动涉及水、气两相间的转换，气相和液相流动的基本方程[20]为：

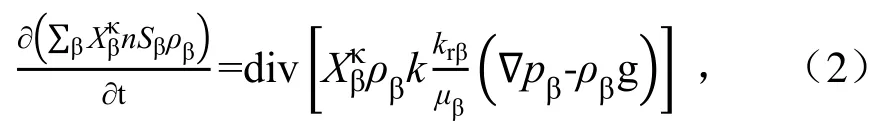
式中：n为孔隙度；b为流体相（气相或液相）；Sb为b相的饱和度；为b相中组分k的质量分数。

2 结果与分析

2.1 临界入渗范围模拟结果

模型设定为25 ℃，先计算一个稳定渗流场作为入渗模型的初始条件。稳定状态下气相饱和度、水相饱和度及毛细压力分布如图2所示。气相饱和度与水相饱和度之和恒为1，且水相饱和度与毛细负压的分布趋势基本一致。

设置不同的入渗范围，模拟不同入渗补给范围条件下包气带中水气两相流运移过程，模拟时长为25 d。取L=8 m和20 m为例，第6天和第14天的模拟结果对比如图3所示。水分在包气带中的入渗以垂向运移为主[21]，对比分析模拟结果，L=20 m湿润锋垂向迁移速率更大，在入渗第14天湿润锋已接近潜水面，而L=8 m时，水分运移明显滞后，由此可初步认定不同入渗范围对包气带中水分运移有显著影响。

刘丽等[22]提出以土体特征含水率定量描述湿润锋，本文参考其思想，以水相饱和度S1=0.5作为湿润锋的特征含水率来确定湿润锋位置。不同入渗范围情况下，湿润锋垂向最大运移距离与时间的关系如图4所示。模拟结果显示，入渗范围L≥16 m时，湿润锋在包气带中的垂向最大运移距离随时间变化基本一致，并几乎在同一时间（第15.8天）到达潜水面；而Llt;16 m时，湿润锋在包气带中的垂向运移先后出现滞后现象，入渗范围L越小，湿润锋运移至潜水面所需的时间越长。

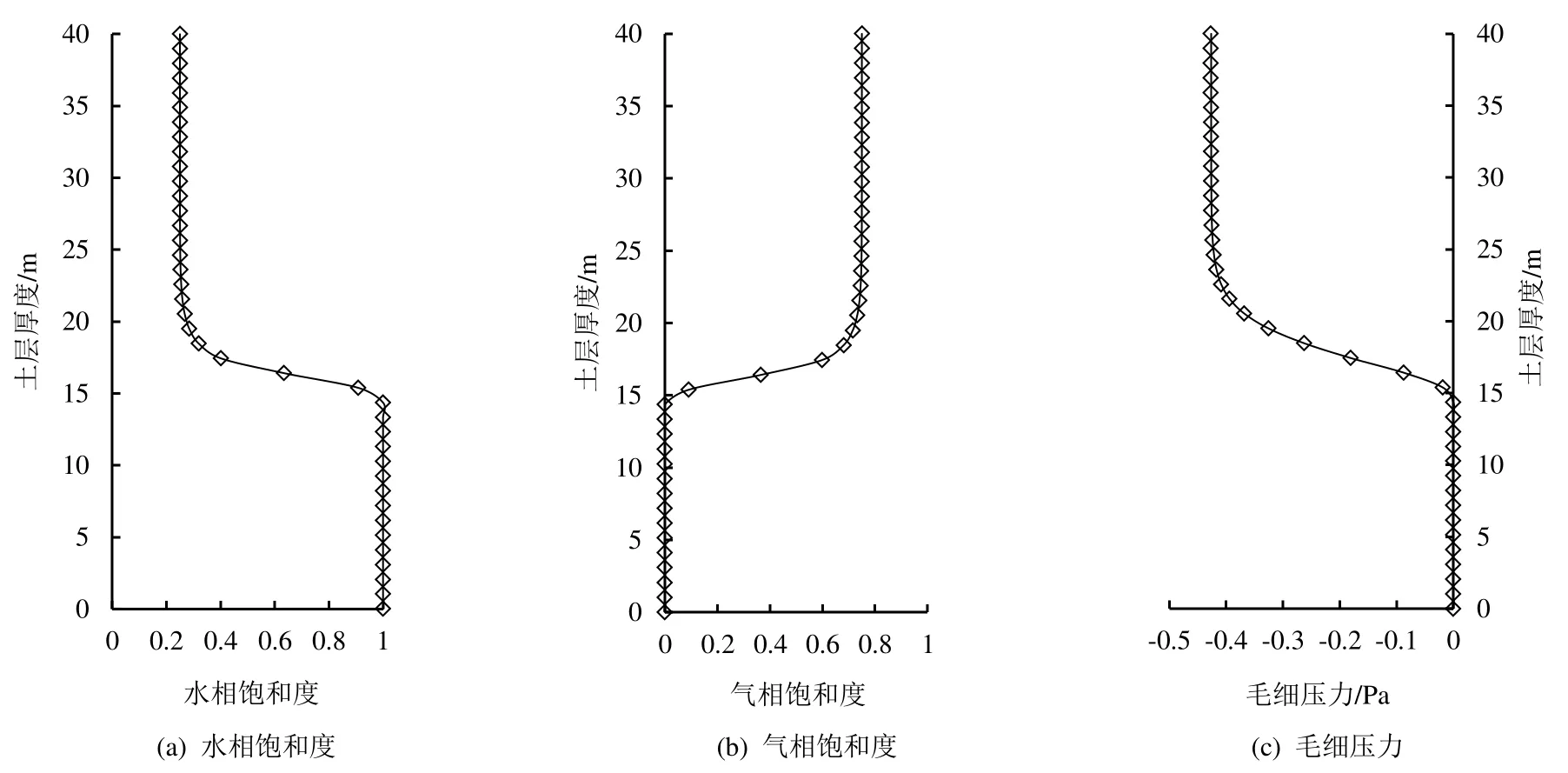
图2 包气带水分入渗模型初始条件Fig.2 Initial conditions of water infiltration model for vadose zone

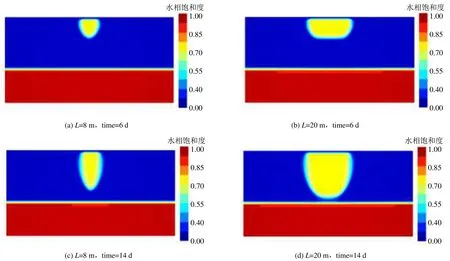
图3 不同入渗范围条件下包气带中水分运移水相饱和度分布Fig.3 Water phase saturation distribution of water transport in vadose zone under different infiltration range

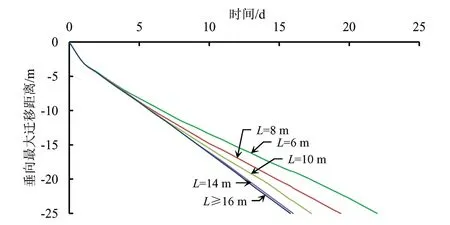
图4 不同入渗范围湿润锋垂向最大迁移距离与时间的关系Fig.4 Relationship between maximum vertical migration dist ance and time of wet front in different infiltration areas

基于上述分析，本文提出临界入渗范围这一概念。以临界入渗范围L0为界线，在此临界值L0上下二侧，不同入渗范围条件下包气带中水分运移规律有着明显差异。Llt;L0时，入渗补给范围越小，水分入渗补给到达潜水面所需时间越长，且延迟性越大；Lgt;L0时，不同入渗补给范围湿润锋在包气带中迁移过程趋于一致，水分同时入渗补给到达潜水面。入渗范围L=8 m和L=20 m条件下的水分运移速度场如图5所示。模拟结果显示补给速率相同时，入渗范围越大，处于中央垂向渗流通道的水流通量越大，垂向水势梯度越大，湿润锋向下迁移越快。

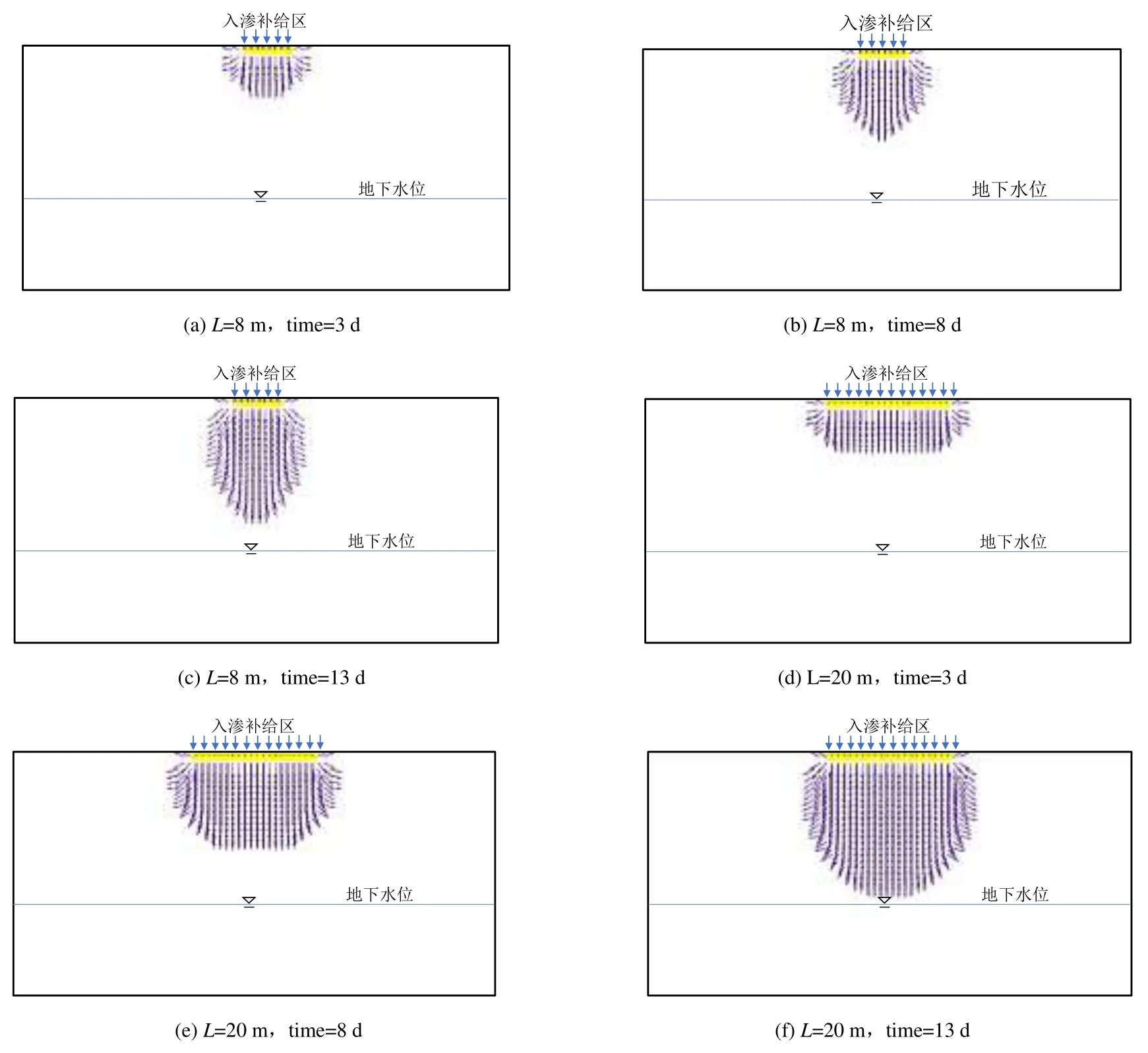
图5 入渗范围L=8 m和L=20 m时，不同时刻包气带水流速场分布Fig.5 Distribution of water velocity field in vadose zone at different time in the infiltration range L=8 m and L=20 m

2.2 临界入渗范围的影响因素分析

影响灌溉水及降水等经浅层土壤包气带入渗补给地下水的因素众多，常见有入渗补给速率、包气带岩性结构特征、包气带厚度、毛管压力、温度以及上覆植被情况[23-24]等。本文对影响临界入渗范围的毛管压力和包气带介质特征等参数进行敏感性分析；并设置不同包气带厚度和不同入渗补给速率模拟情景，研究这些因素对临界入渗范围的影响。

2.2.1 影响临界入渗范围的参数敏感性分析

基于构建的水气两相流数值模型，选取介质孔隙度n，饱和渗透率k，与毛管压力函数相关的拟合参数λ和进气值P0，多孔介质水相残余饱和度Slr以及多孔介质饱水时的水相最大饱和度Sls进行参数敏感性分析。本次敏感性分析采用局部分析法中的因子变换法，分析时保持其他参数不变，仅改变某一参数的值。对照组为表1中概念模型参数值，对n、k、λ、Slr、P0分别进行上下10%、20%的浮动，由于对照组Sls=1，故对Sls仅进行向下10%、20%的浮动。计算结果如表2所示。

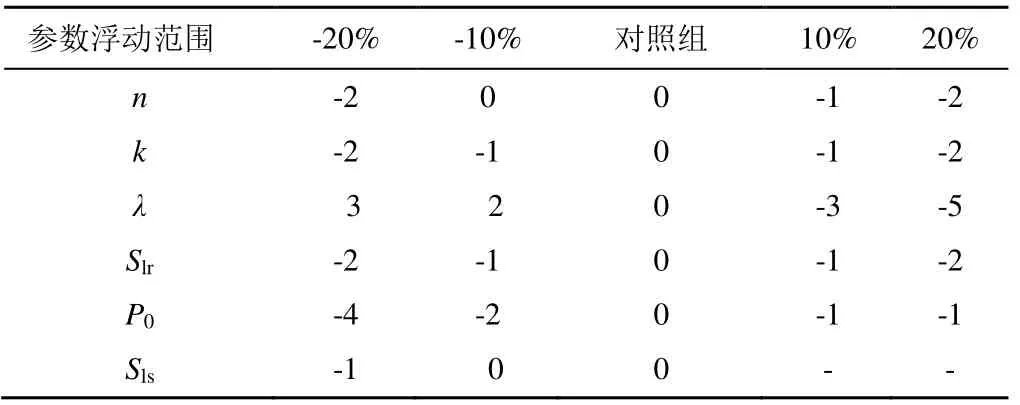
表2 各参数不同变幅情况下的临界入渗范围变幅Fig.2 The critical range variation of infiltration under different parameters m

参数敏感性大小由敏感性指数S衡量：S值越大，表明该参数变化对临界入渗范围的影响越大。S计算公式参见文献[25]。

各参数敏感性指数如图6所示，临界入渗范围对毛管压力函数相关的拟合参数λ最为敏感，进气值P0次之。表明毛管压力的变化对临界入渗范围的影响较大，多孔介质饱水时的水相最大饱和度Sls对临界入渗范围的影响最小。

为进一步验证毛管压力对包气带中水气两相流入渗过程的影响，保持其他条件不变，模拟不考虑毛管压力作用下的情况。入渗范围L=8 m和L=20 m条件下包气带中水气两相流运移6 d的模拟结果如图7所示。对比图7和图3，不考虑毛管压力作用时，湿润锋形态更加平缓，水分迁移速率更快。表明毛管压力对包气带水分入渗有较强的阻滞作用。

2.2.2 包气带厚度与入渗补给速率对临界入渗范围的影响

研究包气带厚度对临界入渗范围的影响，保持恒定入渗补给速率为q=2×10-5m/s，分别设置包气带厚度为15、20、25、30、35 m的5组模型，其他条件不变。模拟计算得到不同包气带厚度对应的临界入渗范围如图8所示。包气带厚度越大，临界入渗范围也越大，二者在给定范围内呈良好的线性相关关系。原因可能是包气带越厚，发生侧向入渗的水分越多，临界入渗范围随之增大。

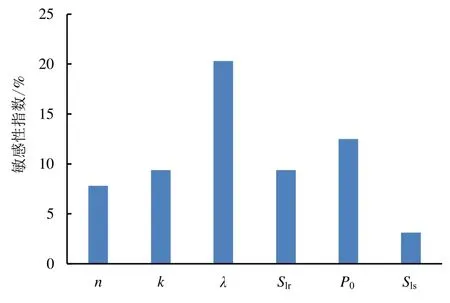
图6 影响临界入渗范围的不同参数敏感性指数对比Fig.6 Comparison of sensitivity indices of different parameters affecting the critical infiltration range

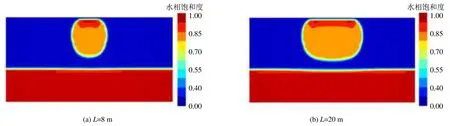
图7 不同入渗范围忽略毛管压力作用下包气带水分运移第6天时水相饱和度分布Fig.7 Water phase saturation distribution on the 6th day of water migration in vadose zone under different infiltration ranges and capillary pressure is ignored

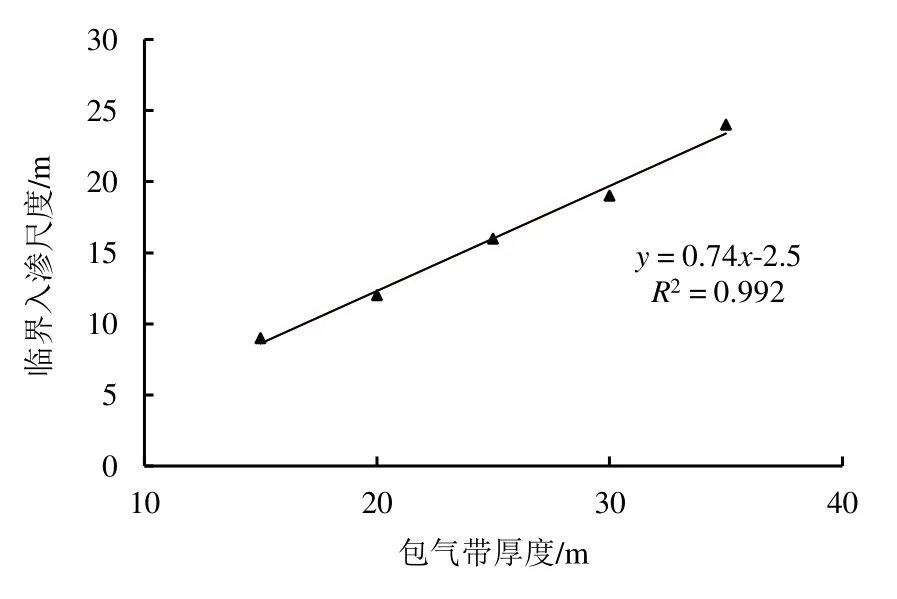
图8 临界入渗范围与包气带厚度的关系曲线Fig.8 The relation curve between critical infiltration range and vadose zone thickness

研究入渗补给速率对临界入渗范围的影响，包气带厚度恒定为25 m，分别设置补给速率为4×10-6、1×10-5、2×10-5、3×10-5、4×10-5、5×10-5m/s的6组模型，其他条件不变。模拟计算得到补给速率与临界入渗范围的关系如图9所示。补给速率越大，临界入渗范围越小，二者在给定范围内呈良好的线性相关关系。原因可能是补给速率越大，单位时间内垂向渗流方向的水分越多，水势梯度相对增大，侧向渗流的强度减弱，临界入渗范围随之减小。

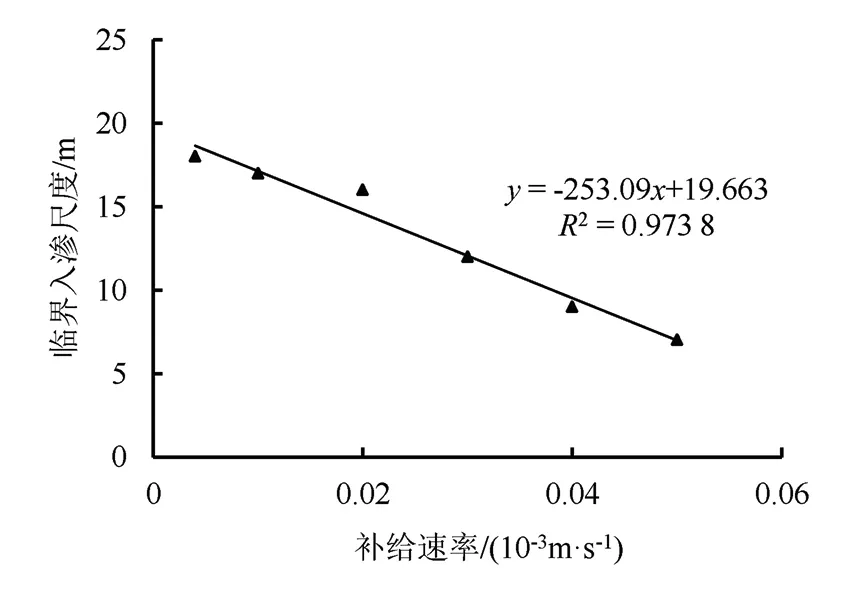
图9 补给速率与临界入渗范围的关系曲线Fig.9 The relationship between recharge rate and critical infiltration range

3 讨 论

本文通过构建水气两相流数值模型研究不同入渗补给范围条件下包气带中水分运移的差异性及其影响因素，数值模拟研究结果表明，水分在包气带中迁移入渗补给地下水前期，本文设定的模型条件下，大致在近地表0～5 m范围内，无论入渗补给范围大小，湿润锋垂向迁移速率始终保持一致，水气两相流在包气带中的迁移基本没有差异性。L小于临界值L0时，垂向迁移速率逐渐变小，L越小，垂向迁移速率变小出现的时间越早，差异性越大；而L大于临界值L0时的垂向迁移速率始终相同，并同时入渗至潜水面，水分在包气带中迁移特征几乎始终保持一致。此外，为进一步弱化模型隔水边界影响，其他条件保持相同，仅将模型零通量边界改成自由边界，相应数值模拟结果表明临界入渗范围依然存在，且在本文设定条件下，L0仍为16 m；不同的是湿润锋到达潜水面的时间有差异：零通量边界模型在入渗补给范围L=16 m条件下，湿润峰到达潜水面所需时间为15.8 d；而对应自由边界模型条件下所需时间为11.6 d。浅层包气带中水分入渗运移过程由于受到重力和毛细压力共同作用会形成垂向流和侧向流。因此，水分在包气带中会形成以垂向运移为主、横向运移为辅的2个方向的迁移过程。正是由于包气带中水分运移存在这个特殊复杂的运动特征，导致不同入渗补给范围会对包气带中水分迁移过程造成影响，从而形成临界入渗补给范围的存在。从水动力角度解释，水分入渗补给范围不同时，处于中央垂向渗流通道的水流通量不同，垂向水势梯度不同。对于入渗补给源对包气带中水分迁移的影响研究，前人很少涉及入渗补给范围，涉及入渗范围的相关研究也未考虑到水分在包气带中的迁移过程。本研究考虑水分在包气带中迁移是水气两相流运移过程，并深入研究入渗补给范围对灌溉水、降水在浅层土壤包气带中迁移的影响，发现临界入渗补给范围，有利于丰富包气带水分运移机制研究，同时对提高灌溉补给效率和节约水资源具有重要意义。但不足的是，涉及临界入渗范围L0影响因素众多，所有影响因素与临界入渗范围的普适性量化关系尚难构建，论文目前开展了影响因素的参数敏感性分析以及包气带厚度和入渗速率的影响，有待继续深入研究临界入渗范围L0与其他影响因素的量化表达。

4 结 论

1）入渗补给范围L对包气带中水分运移具有明显影响，且存在一个临界值L0。Llt;L0时，L越小水分入渗补给到潜水面所需时间越长；Lgt;L0时，水分入渗补给同时到达潜水面。

2）参数敏感性分析结果表明毛管压力对临界入渗范围的影响较大。临界入渗范围对多孔介质水相的残余饱和度Slr，介质孔隙度n和饱和渗透率k较为敏感，而对多孔介质的水相最大饱和度Sls不太敏感。

3）在一定范围内，包气带厚度与临界入渗范围正相关；入渗补给速率与临界入渗范围负相关。

[1] 王大纯. 水文地质学基础[M]. 北京: 地质出版社, 1986: 27.WANG Dachun. Principles of hydrogeology[M]. Beijing: Geological Publishing House, 1986: 27.

[2] 薛禹群. 中国地下水数值模拟的现状与展望[J]. 高校质学报, 2010,16(1): 1-6.

XUE Yuqun. Present situaand prospect of groundwater numerical simulation in China[J]. Geological Journal of China Universities, 2010,16(1): 1-6.

[3] 刘明明. 伊犁河谷区灌溉条件下包气带水分运移规地下水补给研究[D]. 西安: 长安大学, 2019.

LIU Mingming. Moisture movement law and groundwater rechain aeration zone under irrigation conditions in Yili Rivelley[D]. Xi’an:Chang’an University, 2019.

[4] SIMUNEK Jirijirka, BRADFORD Scotta. Vadose zone modeling:introion and importance[J]. Vadose Zone Journal, 2008, 7(2): 581-586.

[5] 高靖勋, 冯洪川, 祝晓彬, 等. 层状非均质结构包气带入渗过程单相流与两相流数值模拟对比研究[J]. 水文地质程地质, 2022, 49(2):24-32.

GAO Jingxun, FENG Hongchuan, ZHU Xiaobin, et al. A comparative numerical simun study of single-phase flow and water-gas two-phasw infiltration process in the vadose zone with the layerheterogeneous structure [J]. Hydrogeology and Engiing Geology, 2022, 49(2): 24-32.

[6] WEI Yunbo, CHEN Kouping, WU Jichun. Estimation of the critical infiltration rate for air compression during infiltration[J].Water Resources Research, 2020,56(4):1-13.

[7] 韦志龙, 蒋勤. 基于WENO-THINC/WLIC模型的水气相流数值模拟[J]. 力学学报, 2021, 53(4): 973-985.

WEI Zhilong, JIANG Qin. Numerical study on water-air two-phasow based on WENO-THINC/WLIC model[J]. Theoal and Applied Mechanics, 2021, 53(4): 973-985.

[8] 高业新, 张冰, 崔浩浩. 包气带水入渗过程中水化学分运移规律研究[J]. 水文地质工程地质, 2014, 41: 1-6.

GAO Yexin, ZHANG Bing, CUI Haohao. A studythe migration of chemical compositions in vadose watenfiltration[J]. Hydrogeology and Engineering Geol, 2014, 41: 1-6.

[9] 徐远志, 赵贵章, 母霓莎, 等. 包气带水分运移过程的因素综述[J].华北水利水电大学学报(自然科学版), 2019, 40(2): 37-41.

XU Yuanzhi, ZHAO Guizhang, MU Nisha, et al. Review on factors affecting the process of watevement in vadose zone[J]. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 2019, 40(2): 37-41.

[10] WEI Yunbo, CHEN Kouping, WU Jichun, et al. Experimental study of the moisture distribution on the wetting front during drainage and imbibition in a 2D sand chamber[J]. Journal of Hydrology, 2018, 561:112-122.

[11] LI Yi, SHAO Mingan. Effects of rainfall intensity on rainfnfiltration and redistribution in soil on Loess slope land[J]. The Journal of Applied Ecology, 2006, 17(12): 2 271-2 276

[12] 臧永歌. 非饱和土降雨入渗规律及其应用的数值研究[D]. 天津:天津大学, 2014.

ZANG Yongge. Numal simulation research on rainfall infiltration and its applion in the unsaturated[D]. Tianjin: Tianjin University, 2014

[13] MORBIDELLI Renato, CORRADINI Corrado, SALTALIPPI Carla, et al. Raininfiltration modeling: A review[J]. Water, 2018, 10: 1 873.

[14] 刘杰, 曾铃, 付宏渊, 等. 土质边坡降雨入渗深度及饱变化规律[J].中南大学学报(自然科学版), 2019, 50(2): 452-459.

LIU Jie, ZENG Ling, FU Hongyuan, et al. Variation law of rainfall infiltration depth and sation zone of soil slope[J]. Journal of Central South University (Natural Science Edition), 2019, 50(2): 452-459.

[15] LAI Jianbin, REN Li. Assessing the size dependency of meas hydraulic conductivity using double-ring infilteters and numerical simulation [J].Soil Science Socief America Journal, 2007, 71(6): 1 667-1 675.

[16] 唐泽华, 盛丰, 高云鹏. 入渗水量和试验尺度对土壤水匀流动的影响[J]. 水土保持通报, 2015, 35(2): 173-178.

TANG Zehua, SHENG Feng, GAO Yunpeng. Effects of tration amount and experimental scale on heterneous soil water flow[J]. Bulletin of Soil and Water Constion, 2015, 35(2): 173-178.

[17] 施小清, 张可霓, 吴吉春. TOUGH2软件的发展及应[J]. 工程勘察,2009, 37(10): 29-34, 39.

SHI Xiaoqing, ZHANG Keni, WU Jichun. The history and applion of TOUGH2 code[J]. Geotechnical Investigation amp; Suying, 2009, 37(10):29-34, 39.

[18] SUN Dongmei, ZANG Yongge, PING Feng, et al. Quasturated zones induced by rainfall infiltration[J]. Tranorous Media, 2016, 112(1):77-104.

[19] 吴吉春. 地下水动力学[M]. 北京: 中国水利水电出版社, 2009:163-168.

WU Jichun. Groundwater hydraulics[M]. Beijing: China Water amp;Power Press, 2009: 163-168.

[20] PRUESS Karsten, OLDENBURG Curtism, MORIDIS Georgej.TOUGH2 User'uide Version 2[J]. Office of Scientific amp; Technical Inforion Technical Reports, 1999.

[21] GLASS Rj, STEENHUIS Tammos, PARLANGE Jeanyves. Wetting front tability as a rapid and far-reaching hydrologic procein the vadose zone[J]. Journal of Contaminant Hydry, 1988, 3(2/4): 207-226.

[22] 刘丽, 吴羊, 陈立宏. 基于数值模拟的湿润锋前进法测量精度分析[J]. 岩土力学, 2019, 40(S1): 341-349.

LIU Li, WU Yang, CHEN Lihong. Accuracy analysis of wetting front advancing method based on numerical simulation[J]. Rock and Soil Mechanics, 2019, 40(S1): 341-349.

[23] 赵文智, 周宏, 刘鹄. 干旱区包气带土壤水分运移及地下水补给研究进展[J]. 地球科学进展, 2017, 32(9): 908-918.

ZHAO Wenzhi, ZHOU Hong, LIU Hu. Advances in moisture migration in vadose zone of drylaand recharge effects on groundwater dynamics[J]. Advas in Earth Science, 2017, 32(9): 908-918.

[24] DU Chaoyang, YU Jingjie, WANG Ping, et al. Analysing the mechms of soil water and vapour transport in the desert vadose zone of the extremely arid region of Northern China[J]. Journal of Hydrology, 2018,558: 592-606.

[25] 李木子, 翟远征, 左锐. 地下水溶质迁移数值模型中的参数敏感性分析[J]. 南水北调与水利科技, 2014, 12(3): 133-137.

LI Muzi, ZHAI Yuanzheng, ZUO Rui. Sensitivity analysis of parameters in numerical simulation of solute transport in groundwater[J]. South-to-North Water Transfers and Water Science amp;Technology, 2014, 12(3): 133-137.

Numerical Simulation of the Influence of Infiltration Range on Gas and Water Flow in Vadose Zone

JIANG Xuncai1, FENG Hongchuan1, ZHU Xiaobin1,2*, WU Jichun1,2, WU Jianfeng1,2, XIONG Guiyao1
(1.Key Laboratory of Surficial Geochemistry, Ministry of Education/School of Earth Sciences and Engineering, Nanjing University, Nanjing 210023, China;2. Key Laboratory of Earth Fissures Geological Disaster, Ministry of Natural Resources, Nanjing 210049, China)

【Objective】To reveal the influence of infiltration recharge range on the water-gas two-phase flow transport process in the package-gas zone based on numerical simulation method.【Method】 Based on the multiphase flow simulation software TOUGH2/EOS3, a numerical model of water-gas two-phase flow was constructed to simulate and analyze the effect of different infiltration recharge ranges on the water infiltration recharge process in the packaged gas zone.【Result】Show that there is a critical infiltration rangeL0, and the water transport pattern in the package-gas zone differs significantly when the infiltration recharge range is larger and smaller than this critical infiltration range. On this basis, the factors affecting the critical infiltration range are further explored. The numerical simulation results show that the change of capillary pressure has a greater influence on the critical infiltration range, and disregarding the effect of capillary pressure will make the water infiltration flow in the package gas zone more concentrated in the vertical direction, at which time the infiltration range has less influence on the water infiltration.【Conclusion】In a certain range, the thickness of the air envelope is positively correlated with the critical infiltration range, and the recharge rate is negatively correlated with the critical infiltration range.

water transport in vadose zone; critical infiltration range; TOUGH2/EOS3; water-gas two-phase flow;numerical simulation

江训才, 冯洪川, 祝晓彬, 等. 入渗补给范围对包气带水气两相流运移过程影响的数值模拟研究[J]. 灌溉排水学报,2022, 41(11): 78-84.

JIANG Xuncai, FENG Hongchuan, ZHU Xiaobin, et al. Numerical Simulation of the Influence of Infiltration Range on Gas and Water Flow in Vadose Zone[J]. Journal of Irrigation and Drainage, 2022, 41(11): 78-84.

P641.2

A

10.13522/j.cnki.ggps.2022273

1672 - 3317（2022）11 - 0078 - 07

2022-05-17

国家重点研发计划场地土壤污染成因与治理技术专项（2019YFC1804300）；国家自然科学基金项目（42072274，41730856，U2167212）

江训才（1997-），男。硕士研究生，研究方向为地下水多相流数值模拟。E-mail: xuncai_jiang@163.com

祝晓彬（1980-），男。副教授，主要从事复杂条件下地下水中污染物迁移数值模拟研究。E-mail: zxb@nju.edu.cn

责任编辑：韩 洋