基于机器学习算法的股指期货价格预测模型研究
2022-12-07杨学威
杨学威
(青海民族大学经济与管理学院,青海 西宁 810007)
1 引言(Introduction)
宏观经济背景、金融市场发展水平和投资者心理预期等多种复杂因素共同驱动金融工具价格变化,使得金融时序价格具有非平稳性、非线性和高噪声的复杂特性[1]。在国内金融市场高速发展的背景下,金融时序价格预测成为一个亟待解决的难题。伴随着人工智能技术的进步,机器学习算法为金融时序价格预测带来了新的研究思路,学界和业界也致力于运用机器学习算法预测各类金融工具短期趋势并构建量化择时策略,以期获取超额投资收益。
随着国内量化投资的兴起,众多金融机构已将机器学习广泛应用于产品定价、风险管理、量化选股、策略管理等领域。对于非线性、非平稳、更新频率快的金融市场数据,相较于传统统计分析方法,机器学习算法能够迅速挖掘出市场上更多潜在信息。本文选用支持向量回归(Support Vector Regression,SVR)、长短期记忆网络(Long Short-Term Memory,LSTM)、随机森林(Random Forest,RF)、极端梯度提升树(Extreme Gradient Boosting,XGBoost)四种常用的机器学习算法构建沪深300股指期货价格预测模型,并利用贝叶斯算法对模型进行超参数优化,比较其预测效果,为量化择时策略开发提供价格预测基础。
2 机器学习算法(Machine learning algorithms)
2.1 支持向量回归
SVR模型利用支持向量机分类的原理,通过在损失函数中加入松弛变量提高模型回归拟合性能[2]。SVR模型能有效处理多维度样本,能够摆脱神经网络预测模型的局部最优问题,达到唯一的全局最优解。SAPANKEVYCH等[3]系统梳理并总结了SVR模型在时间序列预测的相关研究文献。王洪平[4]运用SVR模型根据金融机构贷款余额预测货币供应量。肖阳等[5]基于三种不同的核函数建立了SVR多因子选股模型,并通过网格搜索和交叉验证法确定了模型参数的最优取值,回测结果表现优异,其中高斯核函数绩效表现最优,年化收益达到24.76%。
2.2 长短期记忆网络
LSTM模型属于循环神经网络(Recurrent Neural Network,RNN)的一种,其特殊之处在于RNN仅有记忆暂存的功能,而LSTM兼具长短期记忆功能,解决了RNN存在的长期依赖问题。自HOCHREITER等[6]提出LSTM之后,GERS等[7]又加入了遗忘门对LSTM结构进行完善,自此形成应用至今的LSTM完整结构。AHMED等[8]将损失函数与LSTM模型组合构建外汇损失函数长短期记忆模型(FLFLSTM),预测外汇市场欧元美元汇兑价格,并与其他模型进行对比分析,其研究表明,在外汇市场FLF-LSTM模型预测效果优于其他模型。GIANG等[9]提出了两种基于LSTM的股价预测模型,在美国、德国和越南三个股票数据集上的实验结果表明,此模型在预测股价波动趋势方面优于其他模型。LI等[10]利用差分整合移动平均自回归模型(ARIMA)和LSTM,选取三种股票市场指数的13 个技术指标构建价格预测模型,预测其收盘价并与其他模型进行对比分析,研究结果表明LSTM模型预测精度优于其他模型。
2.3 随机森林
RF作为近年新兴起的、高度灵活的集成算法,具有不易陷入过拟合、抗噪能力强、不用做特征选择、能够平衡误差和处理高维数据且数据集无须标准化及训练速度较快等优点。SIVAMANI等[11]基于社交媒体情感分析,利用包括RF在内的机器学习算法研究投资者情绪对公司股价的影响,研究表明:公众对公司的主观感知可以作为驱动其股价增长的因子。GHOSH等[12]采用RF和LSTM作为训练算法,证明了它们在预测标普成分股价格定向变动方面的有效性。
2.4 极端梯度提升树
XGBoost是陈天奇博士在梯度提升决策树算法的基础上,提出的一种改进算法。XGBoost利用并行化提高其运行速度,同时引入了损失函数的二阶偏导,预测效果更具一般性。衣静[13]通过将集合经验模态分解(EEMD)与XGBoost算法结合,构建了EEMD-XGBoost组合模型,利用模型预测深证综合指数的日收盘价,并对模型进行分析优化。LIU等[14]通过XGBoost筛选评价指标,利用遗传算法优化BP神经网络,构建上证50ETF期权价格预测模型。谷嘉炜等[15]提出XGBoost-ESN的股价预测组合模型,并使用网格搜索法对XGBoost模型和回声状态网络模型(ESN)进行参数优化。研究结果表明,改进的XGBoost-ESN组合模型能有效减少预测误差,对股票价格预测的精度更高。
3 模型基本原理(Model fundamentals)
3.1 SVR模型
SVR模型算法原理如下。

其中,φ(⋅)为映射函数,φ(xi)是将x映射到高维特征空间的特征向量。
SVR的损失函数度量:

损失函数度量在加入松弛变量后:

其中,K(⋅)为核函数,核函数的选择也是SVR算法的关键问题之一。表1中给出了SVR模型常用的几种核函数。本文选用金融时序研究经常使用的高斯核径向基函数(RBF),它具有出色的性能,被广泛应用于分类和回归问题。

表1 常用核函数Tab.1 Commonly used kernel functions
3.2 LSTM模型
LSTM通过对RNN模型结构的优化,能有效避免RNN存在的梯度爆炸或梯度消失问题[16]。LSTM与RNN的区别在于,RNN结构简单,只有一个tanh层,而LSTM内部结构包含四个交互层:遗忘门、输入门、内部记忆单元、输出门。标准RNN结构如图1所示,LSTM结构如图2所示。

图1 标准RNN结构Fig.1 Standard RNN structure

图2 LSTM结构Fig.2 LSTM structure
LSTM中的第一步是通过遗忘门决定信息的丢弃和保留,其结构如图3所示,算法表达式(5)如下:

图3 遗忘门结构Fig.3 Forget gate structure
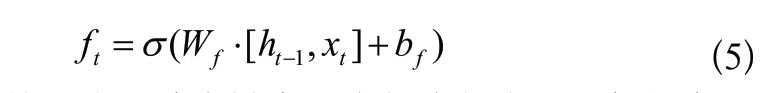
LSTM中的第二步是确定被存放在细胞状态中的新信息,其结构如图4所示,算法表达式(6)如下:

图4 输入门结构Fig.4 Input gate structure


图5 更新状态结构Fig.5 Update state structure

LSTM中的第四步是输出信息,输出前需先进行过滤,其结构如图6所示,算法表达式(8)如下:

图6 输出门结构Fig.6 Output gate structure

3.3 RF模型
随机森林是一种集成学习算法,即利用引导聚集算法(Bagging)和决策树算法(CART)成决策树的过程;它通过采集多个样本集,利用决策树对每个样本集建模,将所有决策树组合起来构建成随机森林,取所有决策树的结果平均值作为随机森林输出。由于各个决策树之间的具有明显的差异度,因此组合出的随机森林具有良好的泛化能力。随机森林的构造过程如图7所示。

图7 随机森林构造过程Fig.7 Random Forest construction process
3.4 XGBoost模型
XGBoost模型通过建立K个回归树,使用贪心算法、二次优化保证每个决策树叶子节点的预测值都是最优解,利用交叉验证选择最好的参数,加入正则化防止过拟合;具有效率高、效果好、能处理大规模数据、支持自定义损失函数等优点[17]。
XGBoost属于Boost集成学习方法,应用串行的基学习器,其中第k个学习器的学习目标是前k-1 个学习器与目标输出的残差,最终的学习器表示如下:
XGBoost的目标函数会加入正则化项,决策树会在后期进行决策树剪枝防止过拟合,加入正则化项后的目标函数如下:

正则化项表示如下:

其中,T是基回归树的叶子节点总数,是基回归树的第t个叶子节点的输出值,γ、λ是正则化项的系数,属于超参数。
当训练第k个基回归树时,前k-1个基回归树的正则化项是一个常数,我们单独把它们提取到C(常数)中,目标函数变成:

将上面推出来的损失函数带回目标函数,化简得到公式(16):

这是T个关于wt的独立二次函数,让每一个二次函数取最小值,即

确定基回归树结构的方法主要是递归地确定叶子节点是否适合被延伸。对于某个我们想要延伸的叶子节点tx,计算其延伸前的目标函数值:

利用贪心算法遍历所有特征的所有可能取值,计算每个取值延伸后的目标函数值,tx分割出两个新的叶子节点t1与t2:

两者求差,表示分割后的信息增益:

取信息增益最大的分割为该叶子节点的最优解。可以设置信息增益取值下限,限制树生长过深,同时通过设置树的最大深度上限防止过拟合。
4 模型建立与超参数优化(Model building and hyperparameters optimization)
本文选取沪深300股指期货主力连续合约(IF9999)自2012 年1 月4 日至2022 年7 月29 日的开盘价、收盘价、最高价、最低价、成交量、成交额作为数据集,以约9∶1的比例将2,569 条交易数据划分为训练集与测试集。本文的训练数据的窗口长度选择收盘价序列ADF检验AIC最小准则计算出的默认滞后阶数25,即用过去25 天的开盘价、收盘价、最高价、最低价、成交量、成交额作为输入特征,未来1 天的收盘价作为标签,进行模型训练。
由于输入指标开盘价、收盘价等与成交量的量纲不同,数量级上的差异会对预测模型收敛带来不利影响,因此需要对原始数据中各项输入指标进行归一化处理,参照常用归一化处理方式如下:

其中,xi是归一化之后的输入数据,分别表示该指标中的最大值与最小值。
为了保持输入数据和输出数据在同一量纲,更真实客观地利用模型评价指标对模型预测能力进行评价,需要对输出数据进行反归一化处理,参照常用反归一化处理方式如下:

模型评价指标参照前人时序数据回归算法预测研究经验,选取R2、均方误差(MSE)、平均绝对误差(MAE)、对称平均绝对百分误差(SMAPE)、适应度函数(LOSS)作为模型评价指标:

4.1 SVR预测模型构建
在构建SVR预测模型时,利用Python中Scikit-learn模块的SVR类实现回归预测,选择径向基函数(RBF)作为核函数,模型在训练集上的预测效果如图8所示。

图8 SVR模型在训练集上预测效果Fig.8 Prediction effect of SVR model on the training set
4.2 LSTM预测模型构建
在构建LSTM预测模型时,利用Python中Keras模块自带的LSTM函数实现回归预测,模型包含输入层、LSTM层、全连接层、输出层。batch_size设置为500,迭代100 次,设置全局随机种子,使用Adam优化器进行优化,模型在训练集上的预测效果如图9所示。

图9 LSTM模型在训练集上预测效果Fig.9 Prediction effect of LSTM model on the training set
4.3 RF预测模型构建
在构建RF预测模型时,利用Python中Scikit-learn模块的RandomForestRegressor实现回归预测,设置子决策树最大树深max_depth为10,子决策树数量n_estimators为200,最小样本叶子数量min_samples_leaf为20,分割所需最小样本数min_samples_split为20,模型在训练集上的预测效果如图10所示。

图10 RF模型在训练集上预测效果Fig.10 Prediction effect of RF model on the training set
4.4 XGBoost预测模型构建
在构建XGBoost预测模型时,利用Python中XGBoost模块的XGBRegressor实现回归预测,设置惩罚项系数gamma为200,子决策树最大深度max_depth为20,子决策树数量n_estimators为100,随机采样比例subsample为0.6。模型在训练集上的预测效果如图11所示。

图11 XGBoost模型在训练集上预测效果Fig.11 Prediction effect of XGBoost model on the training set
4.5 贝叶斯优化
贝叶斯优化算法是一种“黑箱”算法,不需要提前设置目标函数的表达式,即可寻找全局最优解,非常适合本文四种算法的超参数优化。
算法的主体框架不断迭代目标函数后验概率分布与极小值点的过程,使目标函数极小值不断减小,最终得到最优超参数。算法思路如下。
第一步:定义优化目标。

其中,xmin是待优化的超参数,f(x)是待优化的目标函数。
第二步:对观测点进行高斯过程处理。

第三步:不断循环上述过程,最终实现xmin=xt+1,可得到最优化的超参数。
按照上述贝叶斯优化过程,构建优化流程如图12所示。

图12 贝叶斯优化过程流程图Fig.12 Flowchart of Bayesian Optimization process
贝叶斯优化过程中,设置优化次数为200 次。SVR模型优化参数为惩罚因子C和核函数参数gamma;LSTM模型优化参数为全连接层叶子节点数dense_units、学习率learning_rate、隐含层叶子节点数lstm_units_1;RF模型优化参数为子决策树最大深度max_depth、单个决策树使用特征比例max_features、最小样本叶子数量min_samples_leaf、分割所需最小样本数min_samples_split、子决策树数量n_estimators;XGBoost模型优化参数为惩罚项系数gamma、学习率learning_rate、子决策树最大深度max_depth、最小叶子节点样本权重和min_child_weight、子决策树数量n_estimators、L1正则化系数reg_alpha、L2正则化系数reg_lambda、随机采样比例subsample。各个模型优化后在测试集上的表现如图13至图16所示。

图13 优化后SVR模型在测试集上预测效果Fig.13 Prediction effect of the optimized SVR model on the test set

图14 优化后LSTM模型在测试集上预测效果Fig.14 Prediction effect of the optimized LSTM model on the test set

图15 优化后RF模型在测试集上预测效果Fig.15 Prediction effect of the optimized RF model on the test set

图16 优化后XGBoost模型在测试集上预测效果Fig.16 The predicted effect of the optimized XGBoost model on the test set
5 优化后结果分析(Analysis of the results after optimization)
利用贝叶斯优化对各个算法模型进行优化训练后,其超参数选择如表2所示。

表2 贝叶斯优化后超参数选择Tab.2 Hyperparameters selection after Bayesian optimization
根据表3可以看出,优化前RF和XGBoost预测效果显著优于SVR和LSTM,优化后各个算法模型预测效果较为均衡,而贝叶斯优化对于SVR算法预测效果提升最为明显。SVR算法经过贝叶斯优化后,MSE降低了99.54%,MAE降低了94.63%,SMAPE降低了95.06%。可以看出,优化后的SVR算法预测值最接近真实值,预测精度最高。

表3 优化前后评价指标对比Tab.3 Comparison of evaluation indicators before and after optimization
6 结论(Conclusion)
本文利用四种机器学习算法对沪深300股指期货主力连续合约收盘价进行预测研究,验证了机器学习算法对金融时序数据预测的可行性。通过对比贝叶斯优化前后预测效果,验证了贝叶斯优化对于机器学习算法预测效果提升的可得性。研究结果表明,RF和XGBoost可以实现对金融时序数据的准确预测,而贝叶斯优化可以显著提升SVR算法的预测精度。
本文具有选用输入指标过于简略、模型优化方法较为单一的局限性,可通过引入价值、技术、动量、反转、情绪等多种指标构建模型输入,引入遗传算法、粒子群算法、鲸鱼优化算法等多种超参数优化方法提高模型鲁棒性。
